26.06.2013

Metody optymalizacji

Sprawozdanie zajęcia laboratoryjne nr. 3

Temat:

Rozwiązania zadań programowania nieliniowego bez ograniczeń z wykorzystaniem różnych metod.

MTA gr 1

Sekcja:2

sem.6 2012/13

Adam Zieliński

Dariusz Zeman

Celem ćwiczenia było zapoznanie się z zastosowaniem metod bezgradientowych, gradientowych oraz tzw. drugiego rzędu do rozwiązywania zadań ZPN bez ograniczeń.

Treść zadania

Dany jest wspornik o długości l=100m. Belka o stałym przekroju prostokątnym bxh zoatała wykonana z kołowego pręta o średnicy 2r, gdzie r=12m. Wspornik ten został obciążony na końcu siłą równą 0,5 KN. Należy wyznaczyć optymalne wymiary przekroju belki.

Przebieg ćwiczenia

Sformułowani funkcji celu.

Powyższe zadanie wymaga znalezienia dwóch długości prostokątnego przekroju belki, będącymi zmiennymi decyzyjnymi . W tym celu wykorzystany zostaje zależność naprężenia w zginanej belce.

gdzie
x1,x2-zmienne decyzyjne

Funkcja celu : Q(x)=
—> min

Rozwiązania zadania z wykorzystaniem funkcji fminunc służącej do otrzymywania wyników dla ZPN bez ograniczeń. Wybór 5 różnych punktów początkowych i sprawdzenie je funkcją fminunc dla algorytmów metod Quasi-Newtonowskich i Newtona -Raphsona.

clc;

P=500;

l=100;

f=@(x)(6*P*l)/(x(1)*x(2)^2);

x0=[1,1];

options=optimset('HessUpdate','dfp','PlotFcns',@optimplotfval,'Display','Iter');

a=1;

[x,fval,exitflag] = fminunc(f, x0, options)

punkt startowy	x	f(x)	flag	l.iteracji
[1,1]	24,8 35,9	9,3227	1	20
[2,3]	70 98	0,7006	1	22
[5,5]	131 200	0,05	1	23
[10,10]	250 379	0,008	1	23
[12,14]	340 494	0,003	1	23

Tablica wyników dla różnych punktów początkowych

metoda Q-Newtona

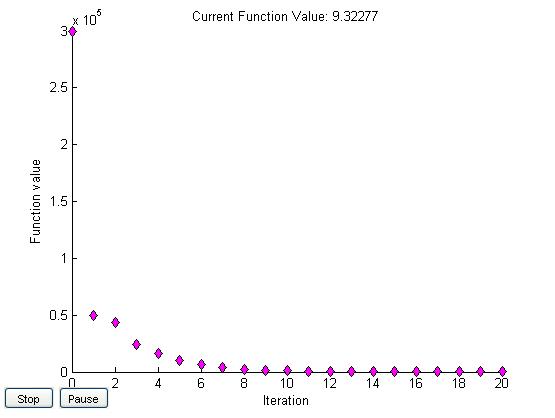
Graficzna reprezentacja wyników

X0=[1,1]

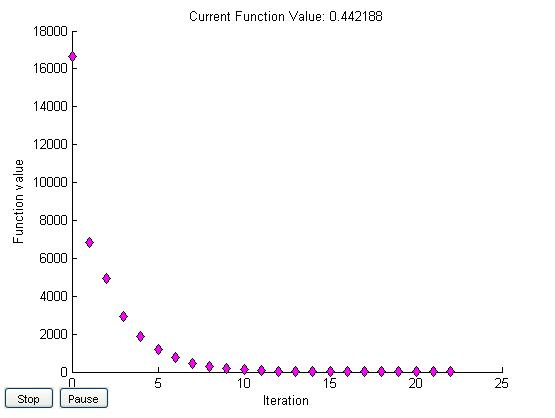
x0=[2,3]

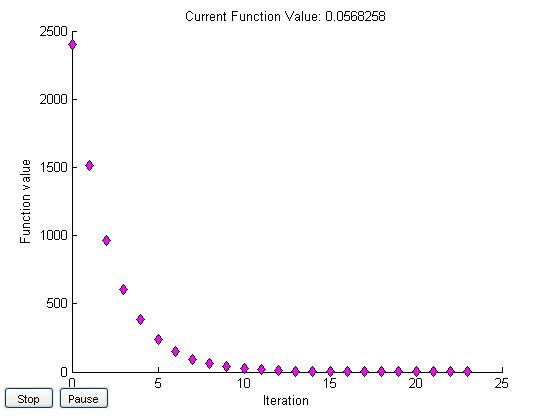
x0=[5,5]

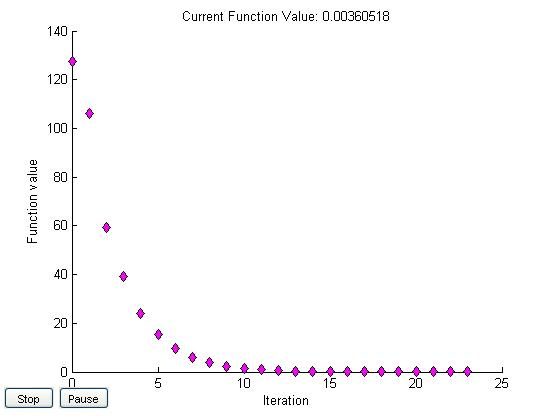
x0=[10,10]

x0=[12,14]

Powyższe wyniki zostały uzyskane dla algorytmu quasi-newtona.

Przez zamianę w kodzie dfp na steepdesc w ustawieniach optymalizacji (optimset),

można uzyskać wyniki dla metody najszybszego spadku.

punkt startowy	x	f(x)	flag	l.iteracji
[1,1]	28 40,3	6,582	1	8
[2,3]	95,4 131,5	0,181	1	2
[5,5]	105,6 184,1	0.08	1	3
[10,10]	125,6 179,4	0,07	0	19
[12,14]	106,4 150,4	0,12	0	25

Tablica wyników dla różnych punktów początkowych

metoda najszybszego spadku

Graficzna interpretacja wyników

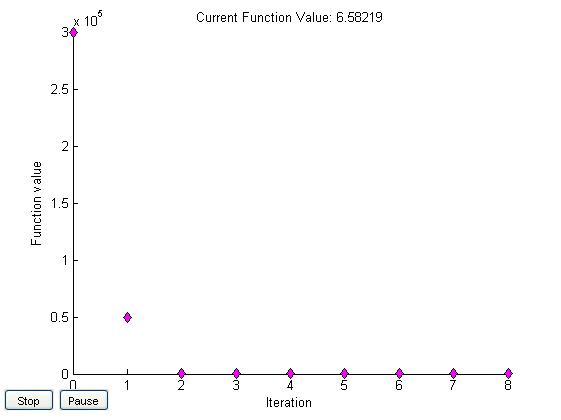
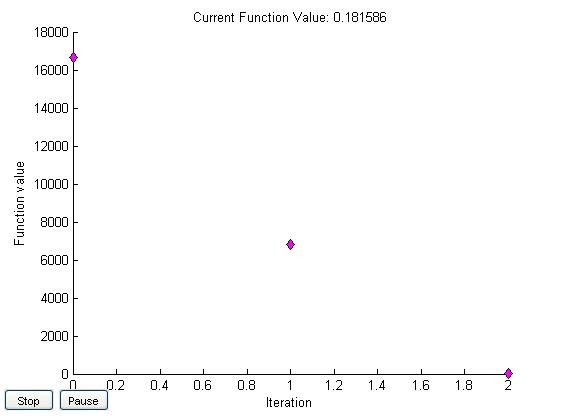
x0=[1,1]

x0=[2,3]

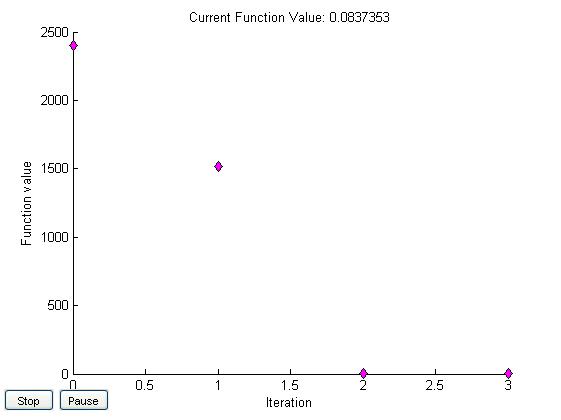
x0=[5,5]

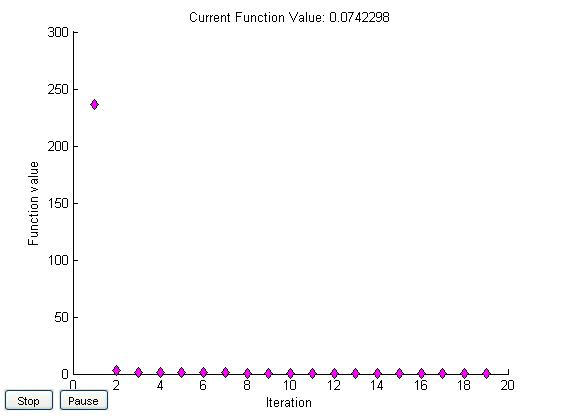
x0=[10,10]

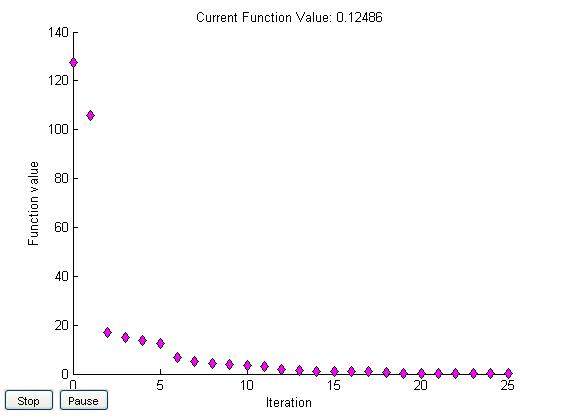
x0=[12,14]

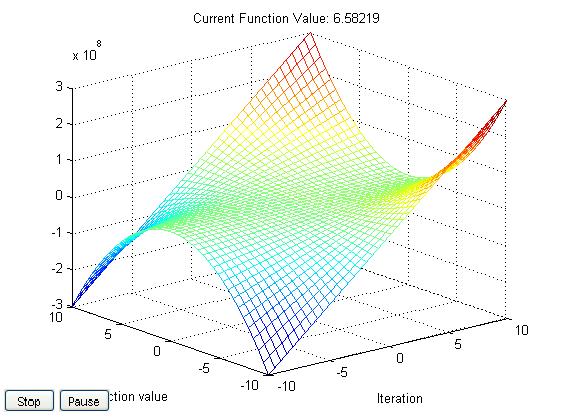
Wykres przedstawiający obszar dopuszczalnych rozwiązań z wybranego przedziału rozwiązań.

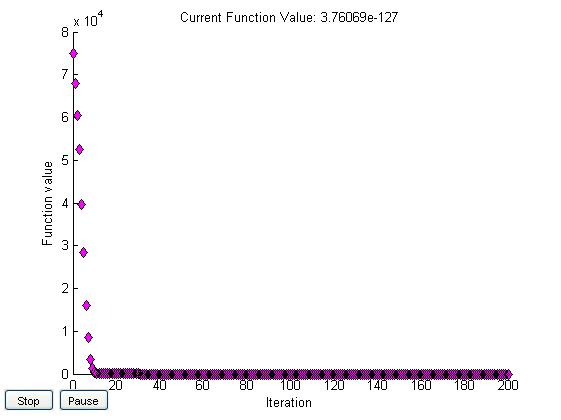
Przykładowy wykres dla funkcji fminsearch zastępującej fminunc dla punktu początkowego x0=[1,1]

Wnioski

-dla różnych punktów rezultaty znacznie się od siebie różnią, co wskazuje że istotnym dla poznanych metod, jest dobór punktu początkowego.

-metoda quasi-newtonowska cechuje się znajdowaniem wyniku dla punktu w zbliżonej liczbie iteracji, w porównaniu do metody najszybszego spadku.

-w obydwu przypadkach wartości funkcji zmniejszają się , wraz z kolejnymi punktami startowymi.

-funkcje fminunc wykazują się szybszym czasem znajdowania rozwiązania, w porównaniu do funkcji minsearch( mniejsza liczba iteracji).

-ze względu na charakter metod rozwiązywania ZPN bez ograniczeń, otrzymane rozwiązania powinny być sprawdzone

---