Metody optymalizacji 2

Program wykładu

• Zadanie programowania nieliniowego
• Warunki optymalności zadania programowania

nieliniowego (warunki Kuhna-Tuckera)

• Relaksacja Lagrange’a
• Dualność w programowaniu nieliniowym
• Obliczenia inteligentne
• Local search
• Symulowane wyżarzanie
• Algorytm ewolucyjny
• Tabu search
• Algorytm mrówkowy
• GRASP

Zadanie programowania

nieliniowego

• Programowanie nieliniowe NLP (ang. Nonlinear

Programming) to klasa problemów programowania
matematycznego, które nie spełniają warunków
programowania liniowego, czyli albo niektóre
ograniczenia albo funkcja celu nie są liniową

• W przypadku kiedy ograniczenia oraz funkcja celu

spełniają specjalne warunki można sformułować
kryteria optymalności dla zadania NLP

• Przybliżoną metodą rozwiązywania zadań NLP jest

przybliżenie nieliniowych funkcji za pomocą funkcji
liniowych i sprowadzenie zadania NLP do klasy LP

Sformułowania zadanie

programowania nieliniowego

Zadanie NLP z ograniczeniami nierównościowymi
min f(x)

xR

n

p.o. g

i

(x)  0 dla i  I

Zadanie NLP z ograniczeniami równościowymi
min f(x)

xR

n

p.o. h

j

(x) = 0 dla j  E

Zadanie NLP
min f(x)

xR

n

p.o. g

i

(x)  0 dla i  I

h

j

(x) = 0 dla j  E

Warunki optymalności

zadania nieliniowego (1)

Definicja. Punkty spełniające ograniczenia zadania NLP

to punkty dopuszczalne

Definicja. Kierunek d wychodzący z punktu x

spełniającego ograniczenia jest dopuszczalny, jeżeli
istnieje



> 0, że dla dowolnego 0 



<



punkt x +



d spełnia ograniczenia zadania

Definicja. W punkcie dopuszczalnym zbiór ograniczeń

zadania NLP można podzielić na dwa zbiory

• Zbiór ograniczeń aktywnych A(x) = {i  I : g

i

(x) =

0}

• Zbiór ograniczeń nieaktywnych, dla których g

i

(x) <

0

Warunki optymalności

zadania nieliniowego (2)

Załóżmy, że funkcje f : X = R

n

 R

1

oraz g

i

: X = R

n



R

1

będą funkcjami różniczkowalnymi oraz niech

jest x



minimum lokalnym rozważanego zadania

NLP.

Niech A(x



) oznacza zbiór ograniczeń aktywnych w x



.

Kierunek dopuszczalny d w x



musi spełniać warunek

g

i

(x



+



d)  0 dla każdego i  A(x



)

Wykorzystując szereg Taylora możemy zapisać

g

i

(x



+



d) = g

i

(x



) +



g

i

(x



)

T

d + O(



)  0

stąd warunkiem koniecznym, aby kierunek d był

dopuszczalny jest

g

i

(x



)

T

d  0 dla każdego i  A(x



)

Warunki optymalności

zadania nieliniowego (3)

Nie zawsze kierunki spełniające powyższy warunek

są kierunkami dopuszczalnymi

Ma to miejsce tylko wtedy, gdy spełnione są pewne

dodatkowe warunki nazwane warunkami
regularności ograniczeń

Ponadto, ażeby punkt x



był punktem minimum, to

każdy kierunek dopuszczalny musi być kierunkiem,
na którym wartość funkcja będzie wzrastać. Stąd
wynika, że w punkcie optymalnym x



dla wszystkich

dopuszczalnych kierunków d musi być spełniona
następująca nierówność

f(x



)

T

d  0

Warunki optymalności

zadania nieliniowego (4)

Lemat Farkasa. Warunki g

i

(x



)

T

d  0  i  A(x



) oraz

f(x



)

T

d  0 oznaczają, że wektor pochodnej

minimalizowanej funkcji celu f(x



) należy do stożka

rozpiętego na wektorach {-g

i

(x



), i  A(x



)} .

To stwierdzenie jest równoważne zapisowi, że wektor

funkcji celu w punkcie optymalnym można zapisać

jako liniowa kombinacja (o niedodatnich

współczynnikach) pochodnych ograniczeń w tym

punkcie

f(x



) =  

iA(x)



i

g

i

(x



)

Współczynniki rozwinięcia



nazywamy mnożnikami

Lagrange’a związanymi z ograniczeniami aktywnymi

Dla ograniczeń nieaktywnych możemy przyjąć wartości

mnożników jako 0

Warunki regularności

Przykładowe warunki regularności
• Wszystkie funkcje ograniczeń g

i

są funkcjami

linowymi

• Wszystkie funkcje ograniczeń g

i

są funkcjami

wypukłymi oraz istnieje punkt x, że g

i

(x) < 0 dla

wszystkich indeksów i  I

• Gradienty wszystkich ograniczeń aktywnych są

liniowo niezależne

Warunki Kuhna-Tuckera (1)

Warunki konieczne optymalności Kuhna-Tuckera dla

zadań z ograniczeniami nierównościowymi

1. f(x) + 

iI



i

g

i

(x) = 0

2. g

i

(x)  0 dla i  I

3.



i

 0 dla i  I

4.



i

g

i

(x) = 0 dla i  I lub 

iI



i

g

i

(x) = 0

Aby przedstawione warunki były warunkami

wystarczającymi muszą być spełnione dodatkowe
warunki regularności

Warunki Kuhna-Tuckera (2)

Warunki konieczne optymalności Kuhna-Tuckera dla

zadań z ograniczeniami równościowymi

1. f(x) + 

jE



j

h

j

(x) = 0

2. h

j

(x) = 0 dla j  E

Warunki konieczne optymalności Kuhna-Tuckera dla

zadań z ograniczeniami równościowymi i

nierównościowymi

1. f(x) + 

iE



j

hj(x) + 

iI



i

g

i

(x) = 0

2. g

i

(x)  0 dla i  I

3. h

j

(x) = 0 dla j  E

4.



i

 0 dla i  I

5.



i

g

i

(x) = 0 dla i  I

Warunki KT – przykład (1)

indeksy
i = 1,2,…,n zmienne (łuki w sieci)
stałe
c

i

przepustowość łuku i

D suma przepływów w sieci
zmienne
f

i

zmienna i (przepływ w łuku i)

minimalizować

min T = 

i

f

i

/(c

i

– f

i

)

ograniczenia

f

i

 c

i

dla i = 1,2,…,n (ograniczenie g

i

)

D – 

i

f

i

= 0 (ograniczenie g)

Warunki KT – przykład (2)

Każde z ograniczeń jest liniowe, ponadto funkcja

kryterialna jest wypukła, więc warunki Kuhna-
Tuckera są w tym przypadku warunkami
koniecznymi i wystarczającymi

Warunki te można zapisać w następujący sposób

c

i

/(f

i

– c

i

)

2

–



+



i

= 0 dla i = 1,2,…,n

(f

i

– c

i

)



i

= 0 dla i = 1,2,…,n

(D – 

i

f

i

)



= 0



i

 0 dla i = 1,2,…,n

Warunki KT – przykład (3)

Z pierwszego warunku otrzymujemy

Pomijając znak „+” otrzymamy, f

i

 c

i,

, co zapewni

spełnienie ograniczeń g

i

dla i = 1,2,…,n.

Ponadto zauważmy, że ze względu na konstrukcję

funkcji kryterialnej musi być spełnione f

i

< c

i

, co

z kolei prowadzi do zależności



i

= 0 dla i = 1,2,…,n

Stąd mamy

i

i

i

i

c

c

f













i

i

i

c

c

f





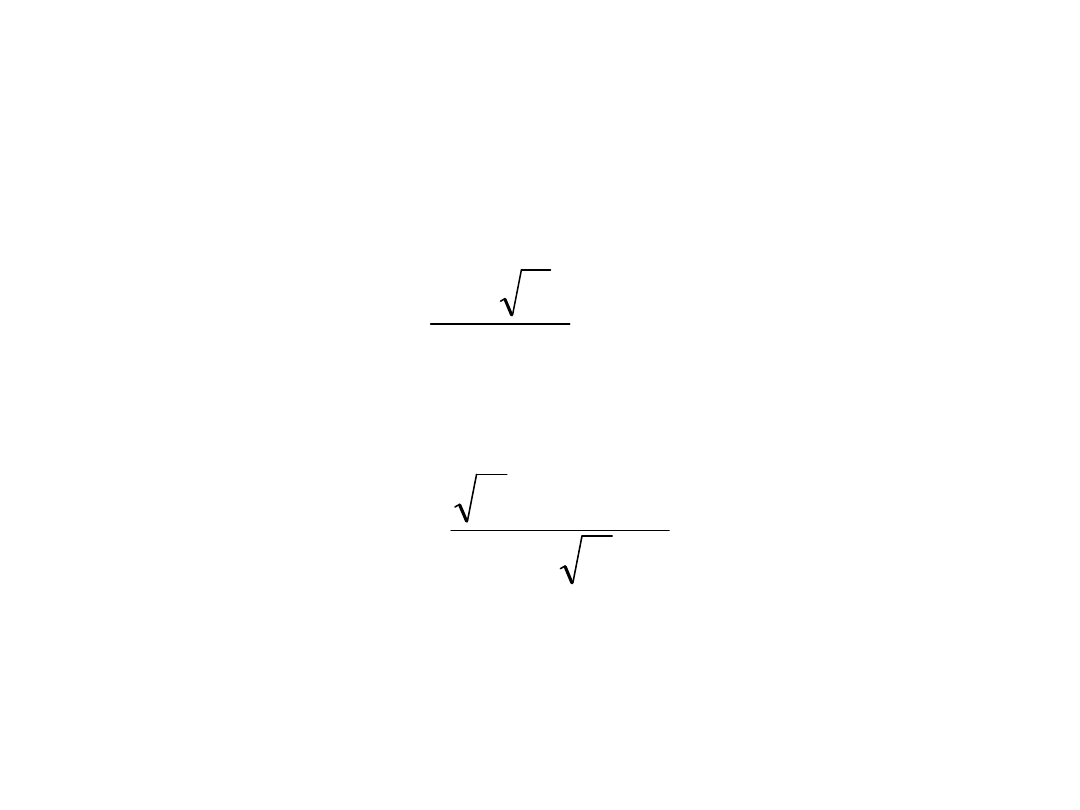
Warunki KT – przykład (4)

Podstawiając otrzymaną wartość do ograniczenia g

otrzymujemy

Podstawiając do poprzedniej zależności mamy

Otrzymane rozwiązanie spełnia ograniczenia

problemu oraz warunki Kuhna-Tuckera, więc jest

optymalne.

2























i i

i

i

D

c

c

















i

i

i i

i

i

i

c

D

c

c

c

f

Funkcja Lagrange’a (1)

Wprowadźmy tzw. funkcję Lagrange’a

L(x,) = f(x) + 

jE



j

h

j

(x) + 

iI



i

g

i

(x) = 0

gdzie  jest wektorem mnożników Lagrange’a,   R

m

Za pomocą funkcji Lagrange’a można zapisać

warunki Kuhna-Tuckera w następujący sposób

1. 

x

L(x,) = 0

2. 



i

L(x,)  0 i  I

3. 



j

L(x,) = 0 dla j  E

4.



i

 0 dla i  I

5. 

iI



i





i

L(x,) = 0

Funkcja Lagrange’a (2)

Definicja. Punkt <x



,



>, 



 0, 



 R

m

, x



 X jest

punktem siodłowym funkcji L(x,), jeśli spełnia

L(x



,



)  L(x,



), x  X

L(x



,



)  L(x



,),   0,   R

m

Twierdzenie. Niech   0 oraz x

 X. Punkt <x



,



>

jest punktem siodłowym funkcji L(x,) wtedy i

tylko wtedy gdy

(a) x



minimalizuje L(x,



) dla x

 X

(b) g

i

(x



)  0 dla i  I

(c)



i

g

i

(x



) = 0 dla i  I

Twierdzenie. Jeśli punkt <x



,



> jest punktem

siodłowym funkcji Lagrange’a L(x,), to x



jest

rozwiązaniem optymalnym zadania NLP

Dualność w programowaniu

nieliniowym (1)

Niech będzie dana funkcja Lagrange’a L(x,)

określona na zbiorach X  R

n

oraz



= { :   R

m

,

  0} o postaci

L(x,) = f(x) + g(x)

przy czym f : X  R

1

oraz g: X  R

m

.

Definicja. Funkcję L

P

(x) nazywamy funkcją

pierwotną, gdy L

P

(x) = f(x), jeśli wszystkie g

i

(x) 

0, + w przeciwnym razie

Definicja. Funkcję L

D

() nazywamy funkcją dualną,

gdy

L

D

() = inf

xX

L(x,)

Dualność w programowaniu

nieliniowym (2)

Pierwotne zadanie optymalizacji można

interpretować jako poszukiwanie takiego x



 X 

R

n

, że

L

P

(x



) = min

xX

L

P

(x)

Dualne zadanie optymalizacji polega na

znalezieniu takiego 







, że

L

P

(



) = min

 



L

D

()

Twierdzenie (o słabej dualności). Niech będzie x

punktem dopuszczalnym zadania pierwotnego.
Niech punkt  będzie punktem dopuszczalnym

zadania dualnego. Wtedy

L

P

(x)  L

D

()

Dualność w programowaniu

nieliniowym (3)

Minimum wartości funkcji celu zadania pierwotnego jest

większe bądź równe maksimum wartości funkcji celu
zadania dualnego

Jeżeli punkt jest x



pierwotnie dopuszczalny, a punkt 



jest

dualnie dopuszczalny oraz f(x



) = L

D

(



) to x



jest

rozwiązaniem optymalnym zadania pierwotnego, a 



jest rozwiązaniem optymalnym zadania dualnego.

Jeżeli zadanie pierwotne jest nieograniczone, to dualna

funkcja celu jest równa minus nieskończoności

Jeżeli supremum w zadaniu dualnym jest równe plus

nieskończoności, to zadanie pierwotne jest
sprzeczne

Dualność w programowaniu

nieliniowym (4)

Definicja. W przypadku gdy obydwa zadania –

pierwotne oraz dualne – mają rozwiązanie
optymalne x



oraz 



, może się okazać, że

f(x



) > L

D

(



)

Mówimy wtedy o tzw. odstępie dualności
Twierdzenie (o silnej dualności). Dla zadania, w

którym funkcja celu jest wypukła, funkcje
ograniczeń nierównościowych są wypukłe, a
funkcje ograniczeń równościowych są liniowe
odstęp dualności wynosi zero

Obliczenia inteligentne

• Obliczenia inteligentne (ang. Computational

Intelligence) to grupa heurystycznych algorytmów

takich jak: sieć neuronowa i obliczenia ewolucyjne,

symulowane wyżarzanie, algorytmy mrówkowe

• Metody obliczeń inteligentnych często mają charakter

stochastyczny, gdyż stosują pewien element

losowy w czasie przeglądania i analizy kolejnych

rozwiązań

• Metody obliczeń inteligentnych to algorytmy

heurystyczne, które potrafią wyznaczyć jednie

przybliżone, suboptymalne rozwiązanie

• Algorytmy rozwiązują problem dyskretny postaci

min F(x) dla x  S

gdzie S to skończona przestrzeń dopuszczalnych

rozwiązań

Local Search (1)

• Metoda Local Search używa pojęcia sąsiedztwa

(ang. neighborhood)

• Sąsiedztwo punktu x  S, N(x) to podzbiór

przestrzeni rozwiązań N(x)  S, takie że x  N(S)

• Główny wymóg dotyczący sąsiedztwa {N(x), x  S}

jest taki, że dla dowolnych punktów x,y  S istnieje

sekwencja punktów z

1

, z

2

,… z

p

należących S do

takie, że z

1

 N(x), z

2

 N(z

1

),… z

p

 N(z

p-1

) oraz y 

N(z

p

)

• Oznacza to, że dowolnego punktu y  S można dojść

z dowolnego punktu x  S przechodząc przez kolejne

sąsiedztwa

Local Search (2)

Metoda Local Search with Steepest Descent (SDLS)

w każdym kroku szuka najlepszego polepszenia

wartości funkcji celu

procedure SDLS
begin
choose initial point(x);
repeat
z := x;
for y  N(x) do if F(y) < F(z) then z := y;

until z = x
end { procedure }

Symulowane wyżarzanie (1)

• Algorytm symulowane wyżarzanie (ang.

simulated annealing SAN) swoje działanie
przypomina zjawisko wyżarzania w metalurgii

• Po wybraniu początkowego punktu x  S i

ustaleniu początkowej temperatury T

0

(zazwyczaj

duża liczba), algorytm przechodzi do wewnętrznej
pętli z ustaloną temperaturą

• Wtedy wewnętrzna pętla jest wykonywana L razy,

polega ona na losowym wyborze sąsiedniego do x
punktu y (y  N(x)) i przeprowadzeniu testu czy

wykonać przejście z x do y

Symulowane wyżarzanie (2)

• Przejście z x do y jest zawsze akceptowane, jeżeli

powoduje polepszenie wartości funkcji celu

• W przeciwnym razie przejście x do y jest

akceptowane z pewnym prawdopodobieństwem
e

-F/T

• Po wykonaniu wewnętrznej pętli L razy, temperatura

jest zmniejszana i wewnętrzna pętla jest
wykonywana ponownie

• Warunek stopu to zmniejszenie się temperatury

do pewnej wartości lub brak poprawy wartości
funkcji celu po dwóch kolejnych zewnętrznych
pętlach

Symulowane wyżarzanie (3)

procedure SAN

begin

choose initial point(x); x

best

:= x; F

best

= F(x

best

);

T := T

0

;

while stopping criterion not true

begin

l := 0;

while l < L do

begin

z := random neighbor(N(x));

∆F := F(z) − F(x);

if ∆F ≤ 0 then

begin

x := z;

if F(x) < F

best

then begin F

best

:= F(x); x

best

:= x end;

end

else if random(0, 1) < e

−∆F/T

then x := z;

l := l + 1;

end

reduce temperature(T);

end

end { procedure }

Algorytm Ewolucyjny (1)

• W większości algorytmów ewolucyjnych (ang.

Evolutionary Algorithm) początkowo losuje się zbiór

rozwiązań dopuszczalnych (zwanych osobnikami), a

następnie poprawia się je za pomocą operatorów

ewolucyjnych (jak mutacja, krzyżowanie, selekcja)

• Algorytm ewolucyjny operuje na populacji osobników
• Populacje krążą w cyklu reprodukcji populacji

rodzicielskiej na populację potomną, operacji

genetycznych na populacji potomnej, oceny

osobników względem zadanego środowiska i sukcesji

osobników potomnych do populacji rodzicielskiej

• Po wielokrotnej iteracji tego cyklu otrzymujemy, z

reguły, osobniki coraz lepiej przystosowane do

środowiska

Algorytm Ewolucyjny (2)

• Chromosom, który jest sekwencją pojedynczych genów

umożliwia zapisanie punktów w przestrzeni rozwiązań

• Funkcja oceny to miara jakości dowolnego osobnika

(rozwiązania) w populacji

• Krzyżowanie polega na połączeniu niektórych

(wybierane losowo) genotypów w jeden

• Popularna metoda selekcji osobników do krzyżowania do

metoda ruletki, wykorzystująca funkcję oceny

• Mutacja wprowadza do genotypu losowe zmiany, jej

zadaniem jest wprowadzanie różnorodności w populacji

• Warunek stopu to wykonanie określonej liczby iteracji

lub brak poprawy wartości funkcji celu po dwóch

kolejnych zewnętrznych pętlach

Algorytm Ewolucyjny (3)

Algorytm ewolucyjny (M + L)
procedure MLEA
begin
initialize(P); k := 0;
while stopping criterion not true
begin
Θ := ∅;
for i := 1 to L do Θ := Θ  crossover(P);

for x  Θ do if random(0,1) < q then

mutate(x);

P := select best(Θ  P)

k := k + 1;
end
end { procedure }

Tabu Search (1)

• Podstawową ideą algorytmu Tabu Search jest

przeszukiwanie przestrzeni, stworzonej ze
wszystkich możliwych rozwiązań, za pomocą
sekwencji ruchów

• W sekwencji ruchów istnieją ruchy

niedozwolone, ruchy tabu

• Algorytm unika oscylacji wokół optimum

lokalnego dzięki przechowywaniu informacji o
sprawdzonych już rozwiązaniach w postaci listy
tabu (TL)

• Twórcą algorytmu jest Fred Glover

Tabu Search (2)

procedure TS

begin

choose initial point(x); F

best

:= F(x); x

best

:= x;

T := ∅;

while stopping criterion not true do

begin

N

∗

:= N(x);

repeat

y := best neighbor (N

∗

);

N

∗

:= N

∗

\{y}

until (y, x)



T ;

update (T );

T := T



{(y, x)};

if F(x) ≤ F

best

then begin F

best

:= F(x); x

best

:= x end;

x := y

end

end { procedure }

Algorytm mrówkowy (1)

• Algorytm mrówkowy (ang. Ant Colony

Pptimization – ACO) został opracowany przez
Marco Dorigo w jego pracy doktorskiej

• Algorytm mrówkowy jest techniką przeznaczona

głównie dla problemów wyszukiwania
najlepszych ścieżek w grafie

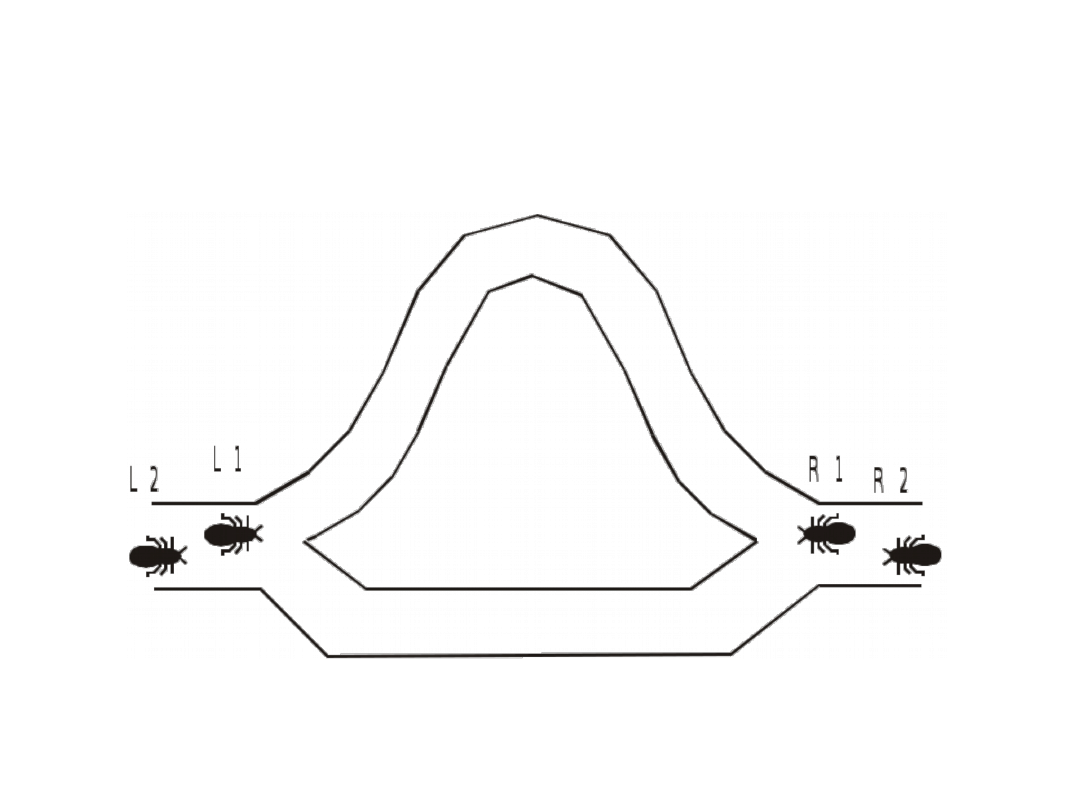
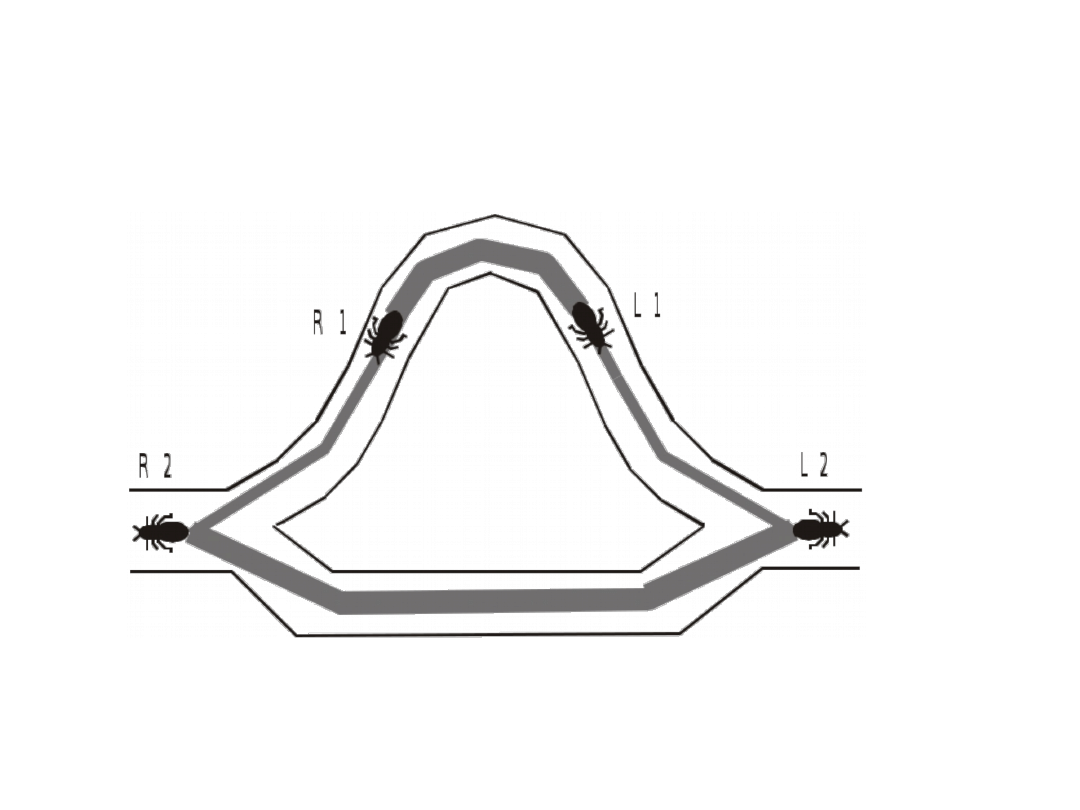
• Inspiracja pochodzi ze świata mrówek, które

potrafią znaleźć najkrótszą trasę między
mrowiskiem a pożywieniem

• Na początku mrówki wędrując w stronę pożywienia

wybierają trasę losowo, ale wracając do mrowiska
pozostawiają na swojej trasie ślad feromonowy

Algorytm mrówkowy (2)

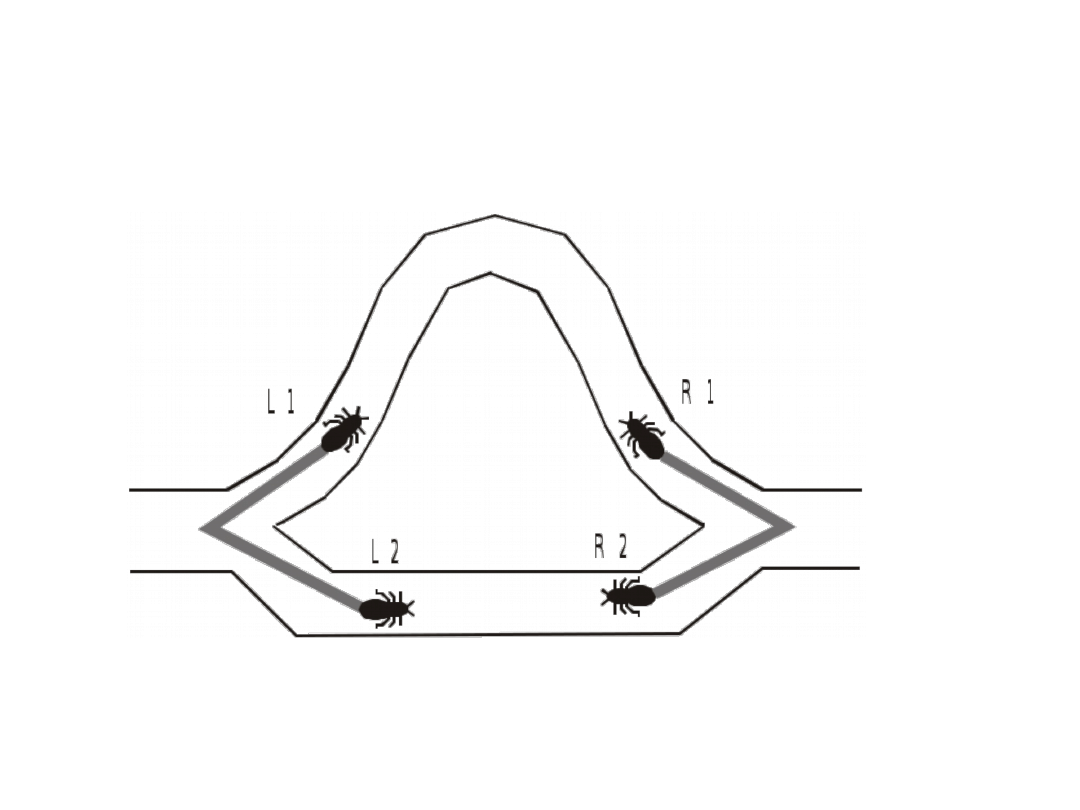
• Feromony stopniowo parują
• Na krótszej trasie parowanie jest stosunkowo

wolniejsze niż na innych trasach, więc kolejne

mrówki wybierają tą trasę chętniej niż inne trasy

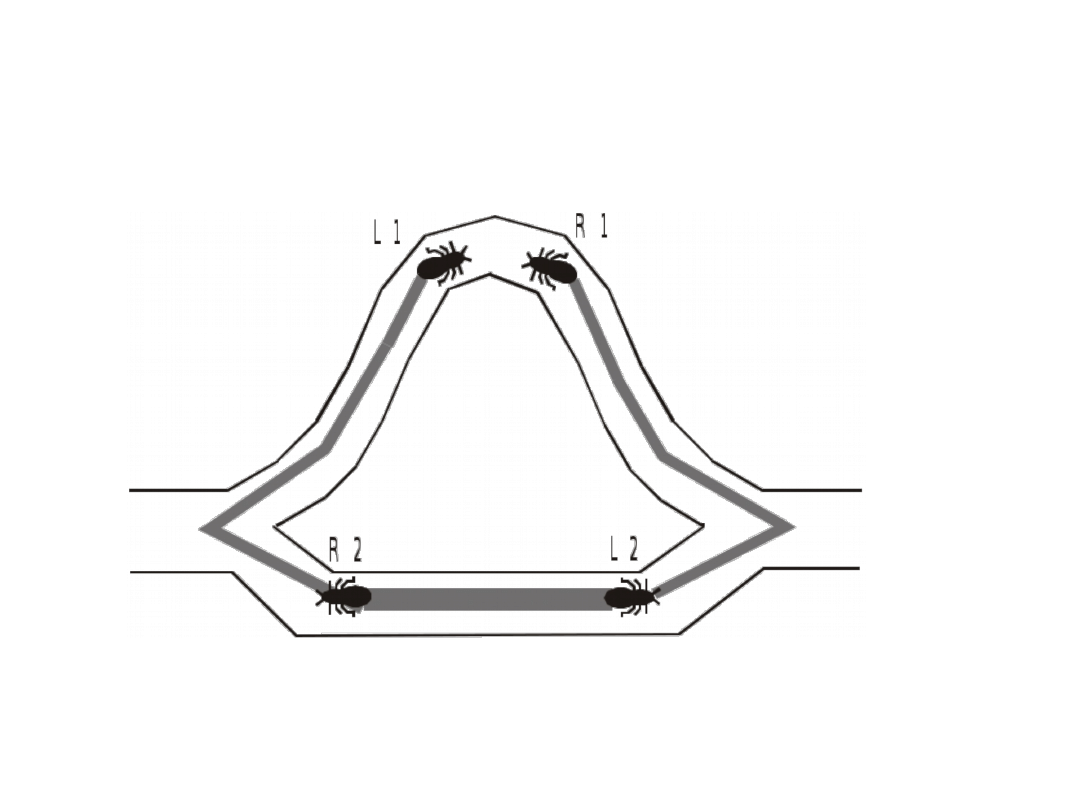
• Kiedy zostanie znaleziona korzystna dla mrówek

trasa, kolejne mrówki wybierają ją chętniej

wzmacniając ślad feromonowy, jest to zjawisko

pozytywnego sprzężenia zwrotnego

• Algorytm mrówkowy został z powodzeniem użyty

do problemu komiwojażera (ang. traveling

salesman problem – TSP) i problemu routing w

sieciach teleinformatycznych

Algorytm mrówkowy (3)

Algorytm mrówkowy (3)

Algorytm mrówkowy (3)

Algorytm mrówkowy (3)

Algorytm mrówkowy (4)

procedure ACO_meta_heuristic()

while (termination_criterion_not_satisfied)

schedule_activities

ants_generation_and_activity();

pheromone_evaporation();

deamon_actions(); {optional}

end schedule_activities

end while

end procedure

procedure ants_generation_and_activity()

while (available_resources)

schedule_the_creation_of_a_new_ant();

new_active_ant();

end while

end procedure

Algorytm mrówkowy (5)

procedure new_active_ant() {ant lifecycle}

initialize_ant();

M = update_ant_memory();

while (current_state  target_state)

A = read_local_ant_routing_table();

P = compute_transition_probabilities(A,M,);

next_state = apply_ant_decision_policy(P,);

move_to_next_state(next_state);

if (online_step_by_step_pheromone_update)

deposit_phermone_on_the_visited_arc();

update_ant_routing_table();

end if

M = update_internal_state();

end while

if (online_delayed_pheromone_update)

for each visted_arc do

deposit_pheromone_on_the_visited_arc();

update_ant_routing_table();

end foreach

end if

die();

end procedure

GRASP (1)

• GRASP (ang. greedy randomized adaptive search

procedure) to metoda polegająca na
wykonywaniu wielu iteracji składających się z
dwóch etapów: konstrukcji rozwiązania oraz
polepszania rozwiązania

• W etapie konstrukcji rozwiązania są generowane

losowe wykorzystując proste heurystyki
zachłanne (ang. greedy) oraz list RCL (ang.
restricted candidate list)

• W drugim etapie, rozwiązanie otrzymane w

pierwszym etapie jest polepszana za pomocą
innych metod, np. local search

GRASP (2)

procedure grasp( f (),g(),maxitr,x*)
x* = ;

for k = 1,2,…,maxitr do
construct(g(),a,x);
local( f (),x);
if f (x) < f (x*) do
x = x*;
end if;
end for;
end grasp;

Podsumowanie

• W przypadku zadań programowania nieliniowego

można dla ułatwienia znalezienia jak najlepszego
rozwiązania zastosować metody relaksacji
Lagrange’a, wykorzystać warunki Kuhna-Tuckera
lub rozwiązać zadanie dualne

• W wielu przypadkach jedyną metodą rozwiązania zadań

dyskretnych o dużym rozmiarze przestrzeni rozwiązań
jest zastosowanie metod obliczeń inteligentnych

• Ważne jest sposób kodowania zadania dla danej

metody inteligentnej

• Nie w każdym przypadku metody obliczeń

inteligentnych sprawdzają się

Dodatkowa literatura

• M. Pióro, D. Medhi, „Routing, Flow, and Capacity Design in

Communication and Computer Networks”, Morgan Kaufman

Publishers 2004 (rozdział 5)

• W. Findeisen, J. Szymanowski, A. Wierzbicki, „Teoria i metody

obliczeniowe optymalizacji”, PWN, Warszawa 1980

• A. Stachurski, A. Wierzbicki, „Podstawy optymalizacji”, Oficyna

Wydawnicza Politechniki Warszawskiej, Warszawa 1999

• G. Di Caro, M. Dorigo, „AntNet: Distributed Stigmergetic Control

for Communications Networks”, Journal of Articial Intelligence

Research 9 (1998) 317-365,

http://www.jair.org/media/530/live-530-1742-jair.pdf

• M. Dorigo, G. Di Caro, „The Ant Colony Optimization Meta-

Heuristic”, in New Ideas in Optimization,

http://citeseer.ist.psu.edu/update/239263

• M. Resende, „Greedy Randomized Adaptive Search Procedures

(GRASP)”, in Encyclopedia of Optimization, Kluwer Academic Press,

1999,

http://citeseer.ist.psu.edu/update/517725

• www.wikipedia.org