Mówimy, że jakieś działanie, proces, układ jest optymalny jeżeli są tak realizowane aby osiągnąć maksimum korzyści przy minimum nakładów ekonomicznych, materialnych i innych.
Zadaniami optymalizacji nazywamy zadania znajdowania punktu, w którym funkcja (funkcjonał) osiąga ekstremum.
Funkcją kryterialną (kryterium funkcją celu) nazywamy funkcję dla której będziemy poszukiwać punktu w którym osiąga ona ekstremum.
Definicja minimum. Funkcja f(x) osiąga w punkcie xmin∈X minimum jeżeli dla każdego x∈X zachodzi f(xmin) ≤ f(x).
Definicja maximum. Funkcja f(x) osiąga w punkcie xmax∈X maximum jeżeli dla każdego x∈X zachodzi f(xmax) ≥ f(x).
Ekstremum silne, spłaszczone, lokalne i globalne.
Jeżeli funkcja kryterialna osiąga minimalną wartość tylko w jednym punkcie x*∈X, a w każdym innym punkcie x∈X różnych od x* zachodzi f(x*) < f(x) to mówimy, że w punkcie x* występuje minimum silne.
Jeżeli zbiór X* ⊂ X zawiera więcej niż jeden element x* taki, że dla każdego x*∈X* zachodzi f(x*)=const. zaś dla każdego x*∈X* oraz, że x∈X - X* zachodzi f(x*)<f(x) to mówimy, że w zbiorze X* funkcja f(x) ma minimum spłaszczone.
Definicja. Funkcja f(x) ma w punkcie x'∈X minimum lokalne, jeżeli istnieje takie otoczenie punktu x' ⊂ X, że dla każdego x∈X' f(x') ≤ f(x) lecz f(x') > f(x*) gdzie x* jest miejscem minimum funkcji dla x∈X.
Warunek konieczny istnienia ekstremum.
Przesunięcie ![]()
en - wektor jednostkowy,
Δxn - przesunięcie zmiennej projektowej,
n - liczba zmiennych projektowych.
Gradient funkcji w punkcie x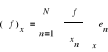
Przyrost wartości funkcji f(x) przy przejściu od punktu
x do x + Δx
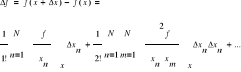

a = (a1, a2, … , aN) b = (b1, b2, … , bN)
![]()
Wniosek - wektor gradientu ![]()
jest prostopadły do każdego wektora przesunięcia dx od punktu x wzdłuż hiperpowierzchni f(x) = const.
Wniosek - spośród wszystkich przesunięć o jednakowej długości funkcja f(x) maleje najszybciej w kierunku wektora gradientu (∇f)x
Wektor ten (∇f)x nazywamy kierunkiem najszybszego spadku funkcji f(x) w punkcie x.
Warunek konieczny istnienia extremum w punkcie x* wewnętrznym zbioru X (∇f)x* = 0
Każda z pochodnych cząstkowych 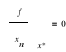
Dla jednej zmiennej kryterialnej ![]()
Punkty, których gradient jest równy zero są punktami stacjonarnymi.
Właściwości zbioru punktów dopuszczalnych.
Jeżeli płaszczyzny są równoległe lub pokrywają się - ograniczenia zdegenerowane.
Jeżeli płaszczyzny przecinają się - ograniczenia niezdegenerowane.
Liczba zmiennych projektowych musi być większa od liczby I ograniczeń równościowych zdegenerowanych N > I.
Warunki ograniczające nierównościowe (w postaci nierówności).
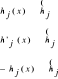
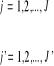
Zbiór wypukły.
Zbiór A nazywamy zbiorem wypukłym jeżeli ztego x'∈A oraz x”∈A wynika, że punkt x'”, którego współrzędne obliczamy
x'” = (1 - α) x' + α x”.
α - jest dowolną liczbą spełniającą warunek 0 ≤ α ≤ 1, należy też do zbioru A.
Definicja. Funkcja wypukła w dół.
Ciągła funkcja f(x), x∈RN jest wypukła w dół w przestrzeni RN jeżeli dla dowolnych dwóch punktów x'∈RN, x”∈RN oraz dla każdego 0 ≤ α ≤ 1 zachodzi: f[x'(1-α) + αx”] ≤ (1-α)f(x') + αf(x”)
Twierdzenie. Jeżeli funkcja kryterialna f(x) jest ściśle wypukła w dół i wypukły jest zbiór X punktów dopuszczalnych to istnieje tylko jeden jedyny punkt minimum w zbiorze X.
Ekstrema funkcji przy braku warunków ograniczających.
Ekstrema funkcji jednej zmiennej.
Warunek konieczny istnienia ekstremum ![]()
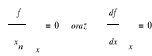
![]()
Rozwijamy funkcję w szereg Taylora.
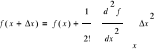
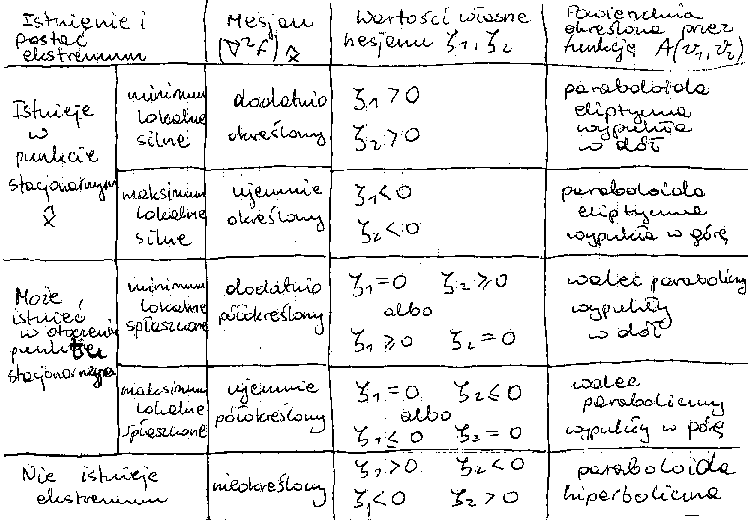
Ekstrema funkcji dwóch zmiennych.

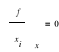
Wyszukiwarka
Podobne podstrony:
testMNłatwy0708, WI ZUT studia, Metody numeryczne, Metody Numeryczne - Ćwiczenia
2. Matlab, aaa, studia 22.10.2014, Materiały od Piotra cukrownika, metody numeryczne w technice, lab
sprawko oczkowawezlowa, aaa, studia 22.10.2014, całe sttudia, III semestr, metody numeryczne lab
Pytania do egzaminu z metod numerycznych (3G), Folder budowlany, Studia Budownictwo Górnictwo, W3G,
sciaga iloraz roznicowy funkcji w punkcie, STUDIA, WIL PK, Metody numeryczne
Sprawdzian ukl rownan, 1 STUDIA - Informatyka Politechnika Koszalińska, muniol, II rok, 3sem, Metody
1EF-DI (MetNum) - Wytyczne projektów, Studia, II Semestr, Metody Numeryczne, Projekty
Matlab co tam, aaa, studia 22.10.2014, Materiały od Piotra cukrownika, metody numeryczne w technice,
strona piotrka, Politechnika Lubelska, Studia, sem III, pen, METODY NUMERYCZNE, metody numeryczbe st
metody numeryczne, Pomoce naukowe, studia, informatyka
metody - egzam, STUDIA, WIL PK, Metody numeryczne
Całkowanie numeryczne, Studia, ZiIP, SEMESTR III, Metody numeryczne
więcej podobnych podstron