Nazwa Geodezja w dosłownym tłumaczeniu z greki oznacza podział ziemi (ge
– ziemia,
daiso – będę dzielił).

Obok matematyki i astronomii jest jedną z najstarszych dziedzin wiedzy.
Należy do nauk zajmujących się pomiarami.

Pomiary te możemy odnieść do niewielkich obszarów obejmujących
pojedyncze działki jak również do całych państw i kontynentów.
 

Pomiary odnoszące się do dużych obszarów stanowią zakres geodezji
wyższej. W pomiarach tych należy uwzględniać krzywiznę ziemi i wprowadzać
odpowiednie poprawki. Geodezję wyższą możemy podzielić na trzy działy

Geodezję matematyczna – zajmuje się ona pomiarami dużych obszarów
oraz obliczeniami, gdy powierzchnię odniesienia stanowi kula lub spłaszczona
elipsoida obrotowa

Geodezję dynamiczna – zajmuje się określeniem kształtu i przebiegu
Geoidy w oparciu o badania grawimetryczne, które polegają na pomiarach
przyśpieszenia i potencjału siły ciężkości.

Geodezję satelitarna, w której pomiary pozwalają na natychmiastowe
wyznaczenie pozycji na powierzchni ziemi, całkowitą automatyzację tych
pomiarów i obliczeń a także wyższą dokładność w porównaniu z metodami
klasycznymi. Pomiary te są również wykorzystywane w badaniach
geodynamicznych do wyznaczania ruchu bieguna, ruchu płyt tektonicznych
itp.

Pomiary odnoszące się do niewielkich obszarów, w których nie
uwzględniamy krzywizny ziemi stanowi zakres geodezji ogólnej
zwanej również geodezją niższą lub potocznie miernictwem.
 
 
Geodezja zajmuje się pomiarami i ich graficzną interpretacją.
Ostatecznym wynikiem prac są najczęściej mapy wykonywane
w różnych skalach obrazujące powierzchnię ziemi lub jej
niewielki fragmenty. Zobrazowanie takie może być
sytuacyjne, wysokościowe
lub sytuacyjno - wysokościowe.

Ze względu na realizację różnych zadań geodezję możemy
podzielić na następujące działy:
 

Geodezja ogólną – zajmuje się pomiarami sytuacyjnymi i
wysokościowymi oraz wykonywaniem map
wielkoskalowych, które możemy odnieść do płaszczyzny.

Geodezja wyższą

matematyczną

dynamiczną

Satelitarną

Kartografia – zajmuje się podstawami matematycznymi
sporządzania map w celu przedstawienia zakrzywionej powierzchni
ziemi lub jej części na płaszczyźnie w wyniku wybranego
odwzorowania kartograficznego.

Topografia – zajmuje się pomiarami terenu z uwzględnieniem
rzeźby i sporządzaniem map topograficznych w skalach od 1:5000
do 1:100000 głownie do celów wojskowych

Fotogrametria – zajmuje się wykonaniem zdjęć naziemnych,
lotniczych i satelitarnych. Po ich przetworzeniu realizuje się mapy,
plany. Można również na ich podstawie badać i obserwować zjawiska
zachodzące na powierzchni Ziemi (w czasie rzeczywistym).

Instrumentoznawstwo – zajmuje się konstrukcją i badaniem
instrumentów geodezyjnych

Rachunek wyrównawczy – zajmuje się obliczeniami i
wyrównaniem wyników pomiarów, określeniem wielkości
najprawdopodobniejszych, określeniem błędów pomiarów i oceną
dokładności.

Geodezja gospodarcza – stosowana jest w różnych dziedzinach
gospodarki np. geodezja górnicza, kolejowa, leśna, wodna, rolna i
inżynieryjno przemysłowa.

Astronomia geodezyjna – zajmuje się określeniem położenia
punktów na powierzchni ziemi w oparciu o obserwację ciał
niebieskich.

Powierzchnie odniesienia
 
 
Powierzchnie, na która rzutuje się pomierzone punkty
nazywamy powierzchnią odniesienia.
W zależności od wielkości obszaru objętego pomiarem
powierzchnia odniesienia dla określenia sytuacyjnego
pomierzonych punktów stanowić może:

 
kulę
elipsoidę obrotową
płaszczyznę

Powierzchnię odniesienia dla pomiarów wysokościowych
stanowi geoida – teoretyczna powierzchnia powstałą w
wyniku przedłużenia średniej powierzchni mórz i oceanów pod
lądami i nad depresjami. W stosunku do tak przyjętej
powierzchni oblicza się wysokości punktów na powierzchni
ziemi.
 

Geoidą nazywamy powierzchnię, która w każdym punkcie
przecina pod kątem prostym kierunek siły ciężkości. Na skutek
występowania gór i dużych zbiorników wodnych oraz
nierównomiernego rozmieszczenia mas w skorupie ziemskiej
kierunek siły ciężkości ulega pewnym odchyleniom i nie jest
taki, jaki by był gdyby skorupa ziemska była by jednorodna.
Powierzchnia geoidy, przecinająca stale pod kątem prostym
zmienny kierunek pionu nie jest, więc powierzchnią
matematyczną, lecz fizyczną i nie da jej się przedstawić
postaci równania matematycznego.

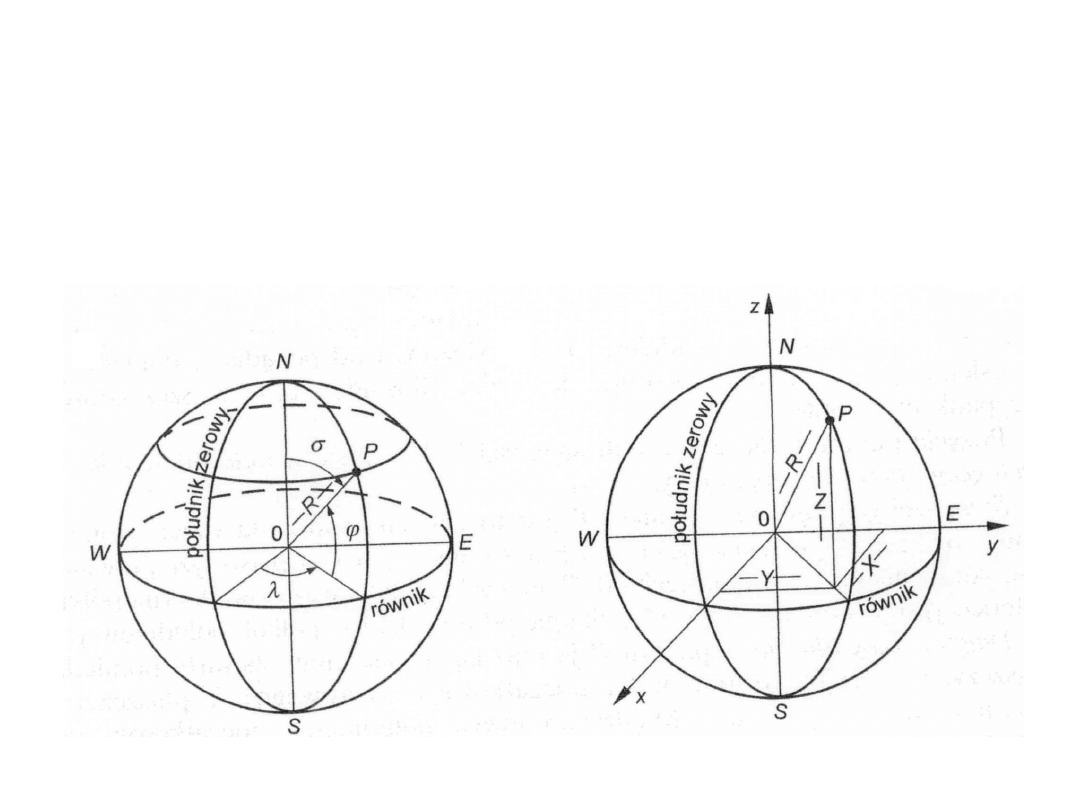
Układy współrzędnych
 
W geodezji stosuje się różne układy współrzędnych. Położenie
dowolnego punktu P leżącego na kuli będzie określone
jednoznacznie przez podanie współrzędnych geograficznych tj.
dwóch kątów: zwanych szerokością i długością geograficzną.
Można również określić położenie punktu podając jego
współrzędne prostokątne X, Y, Z,
 

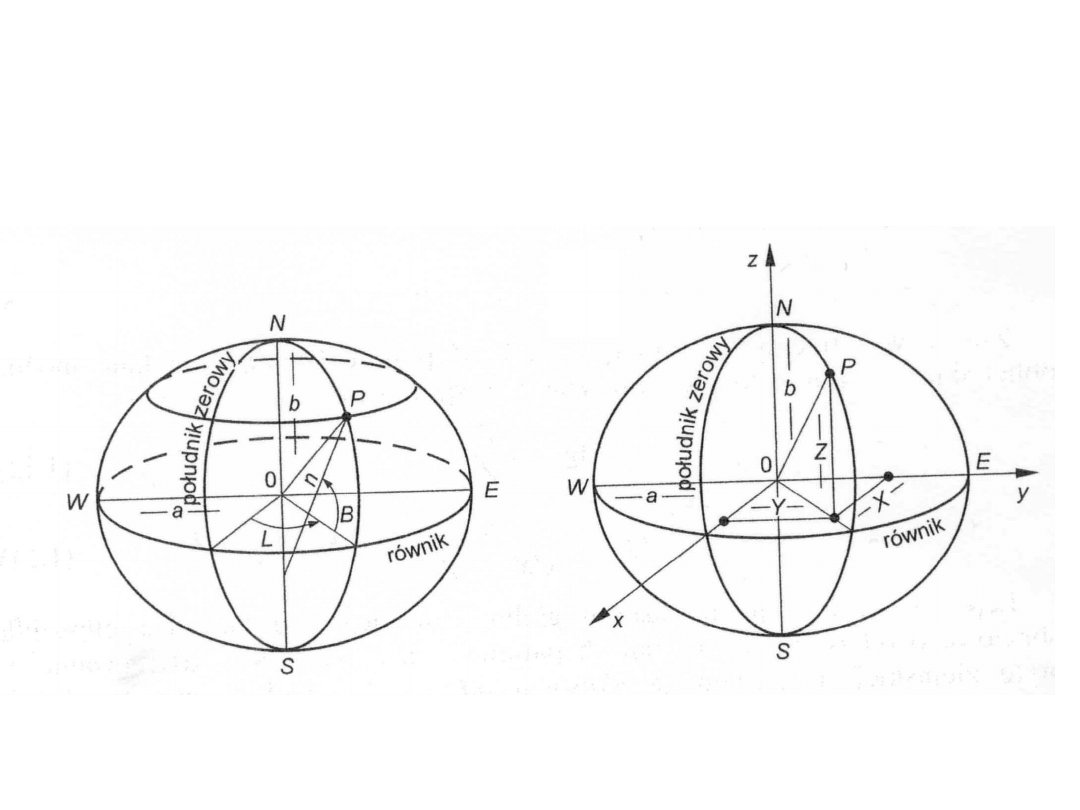
W przypadku elipsoidy położenie punktu P określimy
jednoznacznie podając dwa kąty B i L nazwane szerokością i
długością geodezyjną. Możemy również określić podobnie
jak w przypadku kuli położenie punktu w układzie
współrzędnych prostokątnych X, Y ,Z

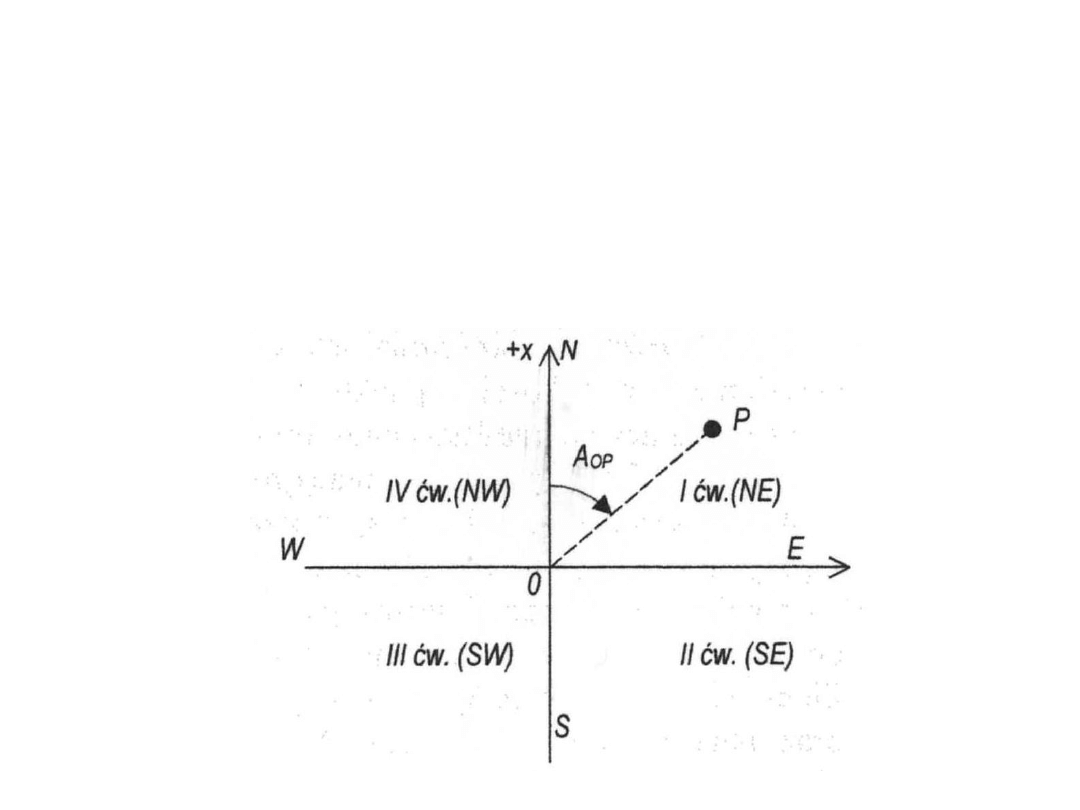
W geodezji na płaszczyźnie stosowany jest układ współrzędnych
prostokątnych, który różni się od układu znanego z matematyki
usytuowaniem osi x i y, kierunkiem liczenia kątów i kierunkiem
numeracji ćwiartek. Pionowa oś x tego układu o dodatnim kierunku jest
zgodna z kierunkiem północy, a dodatni kierunek osi y skierowany jest
na wschód. Układ taki nazywamy prostokątnym geodezyjnym. Jest on
układem prawoskrętnym, liczenie kątów i ćwiartek jest zgodne z
ruchem wskazówek zegara. Prawoskrętność układu oraz zamiana osi
powodują pełną zgodność wzorów geometrii analitycznej oraz znaków
funkcji trygonometrycznych.

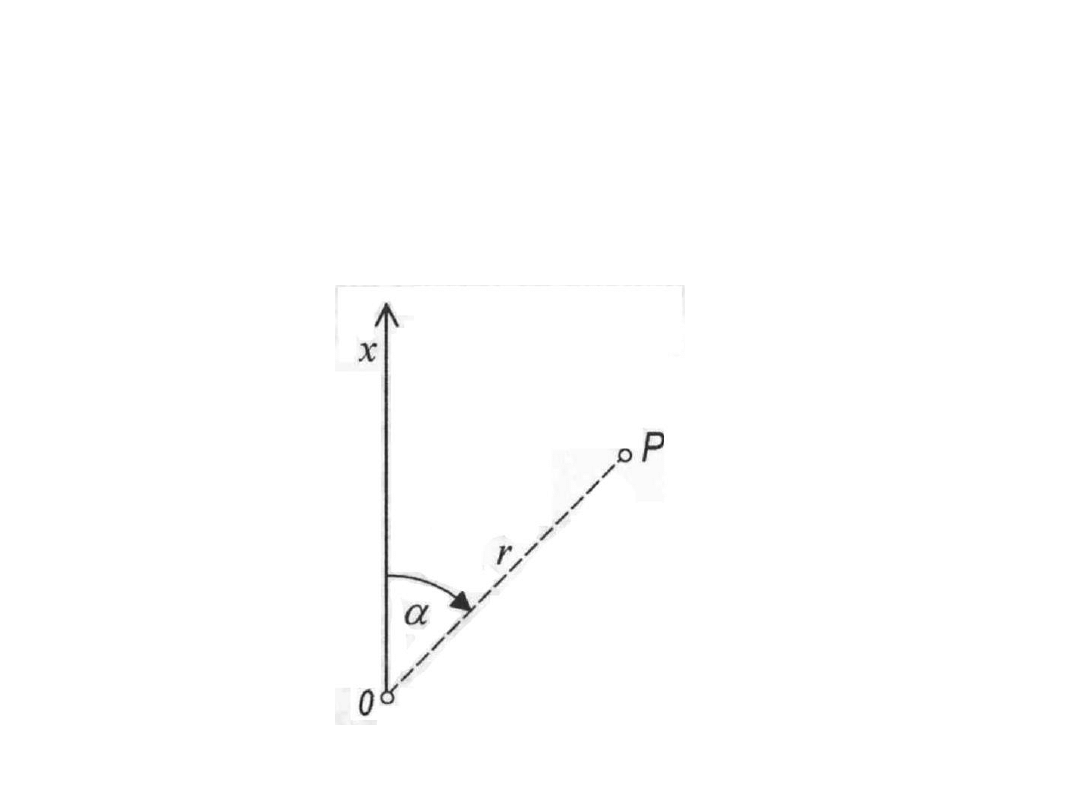
Położenie punktu P określamy podając dwie współrzędne X i Y
natomiast orientację odcinka OP określamy poprzez podanie
azymutu, który jest (najogólniej) kątem zawartym pomiędzy
kierunkiem północy a danym kierunkiem liczony zgodnie z ruchem
wskazówek zegara, czyli w prawo. Znając współrzędne
prostokątne punktu P oraz punktu O w prosty sposób ze
współrzędnych prostokątnych możemy przejść na współrzędne
biegunowe określając długość odcinka OP i kąt

Układ wysokościowy
 
 
 
Na terenie Polski obowiązuje państwowy układ wysokości,
które tworzą wysokości normalne odniesione do średniego
poziomu Morza Bałtyckiego w Zatoce Fińskiej wyznaczonej dla
mareografu w Kronsztadzie koło Sankt Petersburga (Federacja
Rosyjska).

W układzie tym wyznaczone są wysokości punktów
podstawowej osnowy wysokościowej.

W oparciu o te punkty wykonujemy pomiary niwelacyjne na
podstawie, których określa się wysokości punktów osnowy
szczegółowej i pomiarowej.

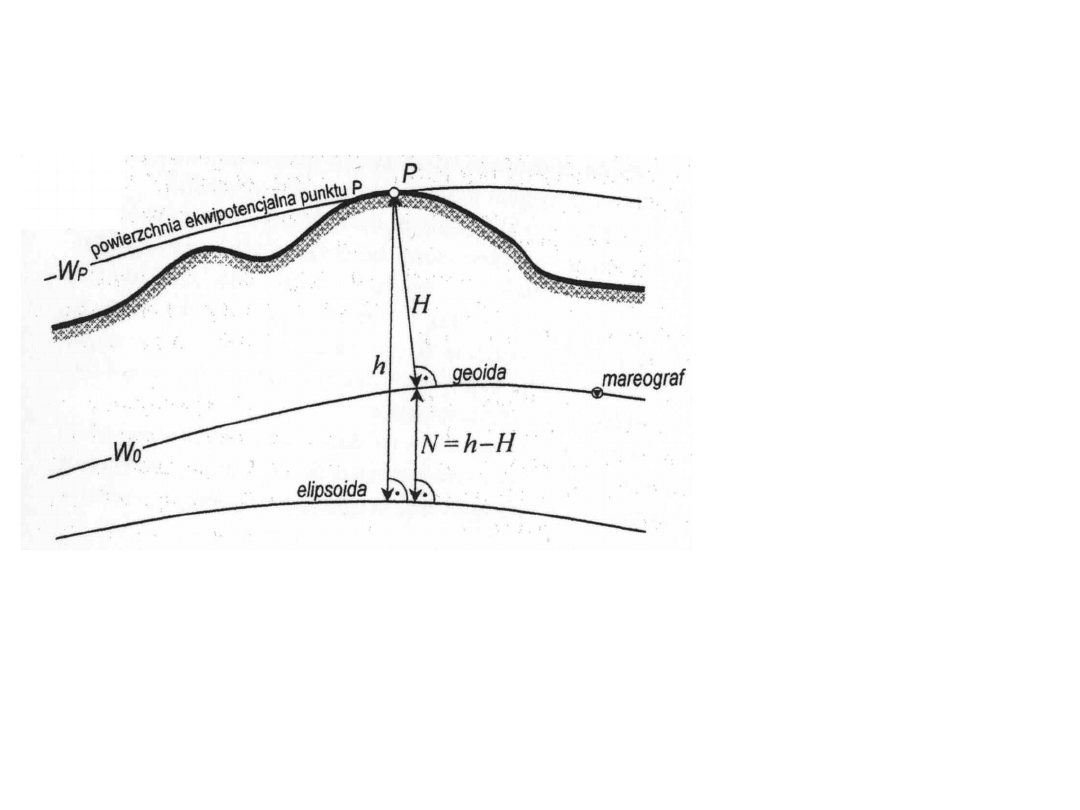
H – wysokość
normalna
 
h - wysokość
elipsoidalna (wysokość
geodezyjna)
 
N – odstęp geoidy od
elipsoidy

Podstawowe wiadomości z kartografii
 Najczęściej spotykaną formą opracowań geodezyjnych są mapy.
Jedna z ogólnych definicji brzmi: Mapa – jest graficznym obrazem
powierzchni Ziemi lub jej mniejszych obszarów przedstawionym na
płaszczyźnie. Obraz ten jest zmniejszony, określony matematycznie,
uogólniony, sporządzony z zastosowaniem umownych znaków.

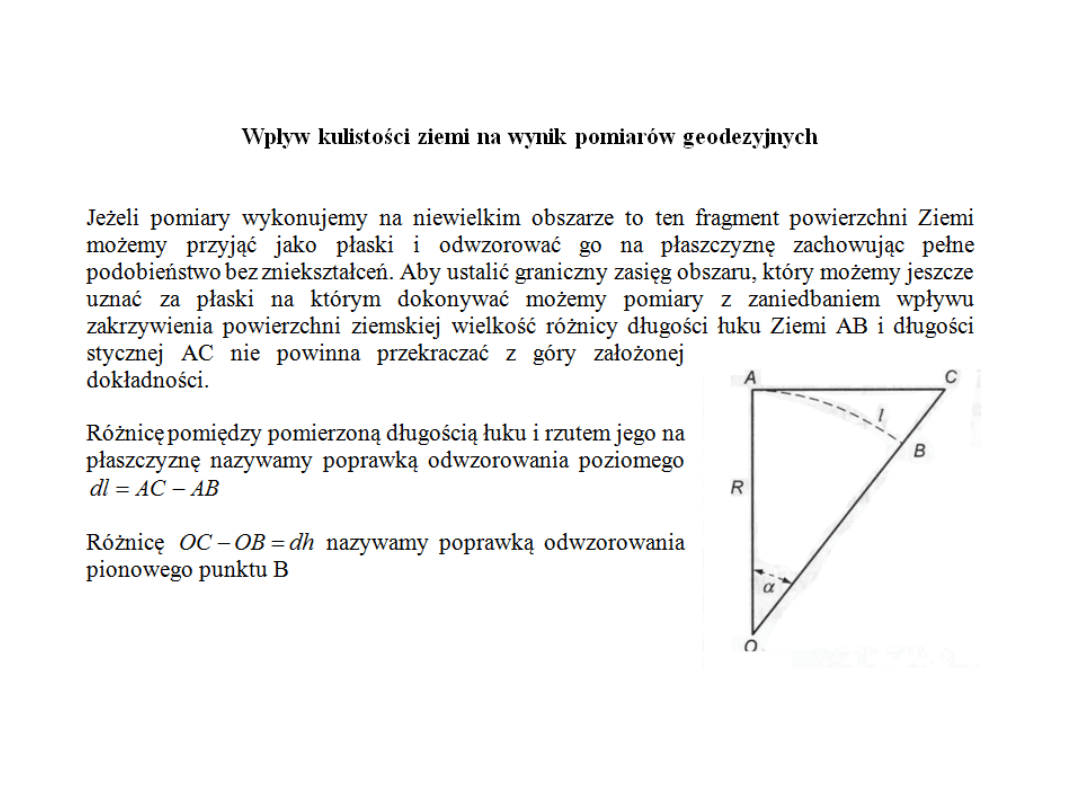
Przekształcenie obszaru kulistego na obszar płaski nazywamy
odwzorowaniem.
Powierzchni kuli lub elipsoidy nie da się przedstawić (odwzorować na
płaszczyźnie) bez zniekształceń, ale w zależności od przyjętego
rozwiązania zniekształcenia te mogą być różne.

Ze względu na rodzaje zniekształceń odwzorowania możemy
podzielić na:

równokątne, konforemne – kąty na mapach równe kątom w terenie

wierno powierzchniowe, równo polowe – powierzchnie na mapie
odpowiadają proporcjonalnie do skali powierzchnią w terenie.

wierno długościowe – pewne odcinki na mapach wzdłuż południka
lub równoleżnika nie są zniekształcone

dowolne – występują wszystkie zniekształcenia – kątów, powierzchni
i odległości

Ze względu na rodzaj powierzchni, na którą odtwarzamy
powierzchnię oryginału odwzorowania dzielimy na:

płaszczyznowe

walcowe

stożkowe

umowne

Współcześnie dla celów geodezyjnych i kartograficznych
najczęściej stosuje się odwzorowanie Gaussa – Krugera, które
stosowane jest również w Polsce.

Jest to odwzorowanie równokątne, walcowe, poprzeczne.
Południk środkowy obszaru odwzorowuje się wiernie.

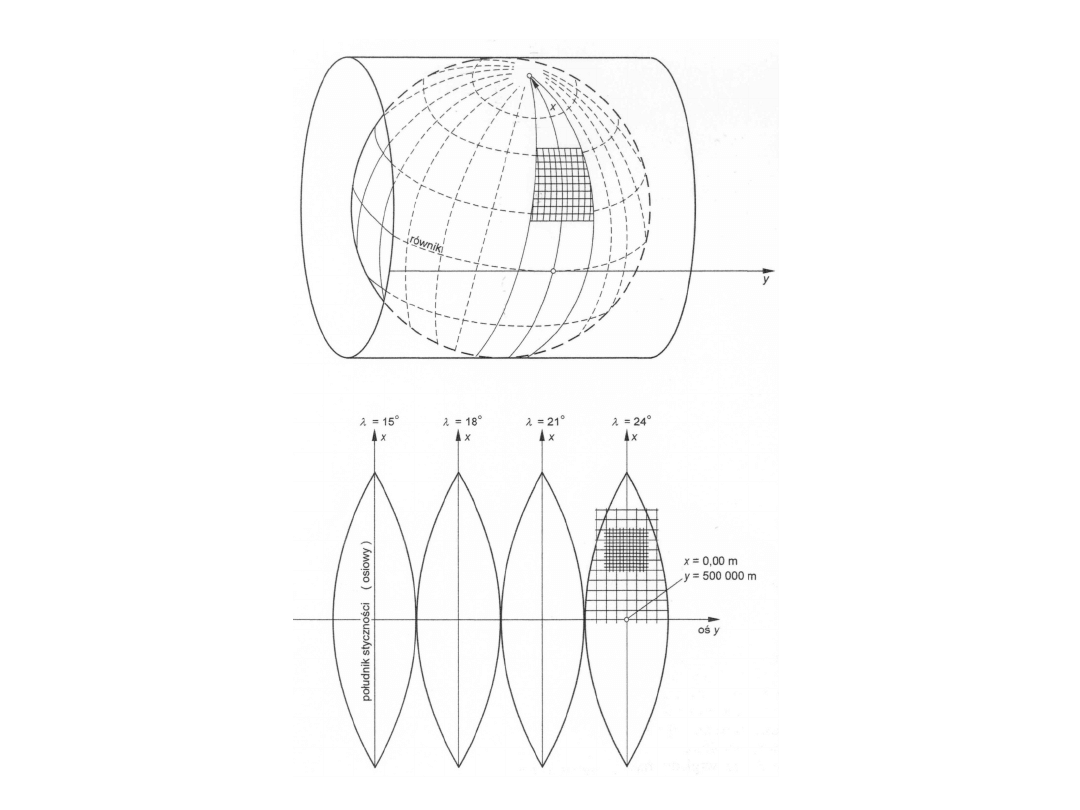
Jednakże całej powierzchni elipsoidy nie możemy odwzorować
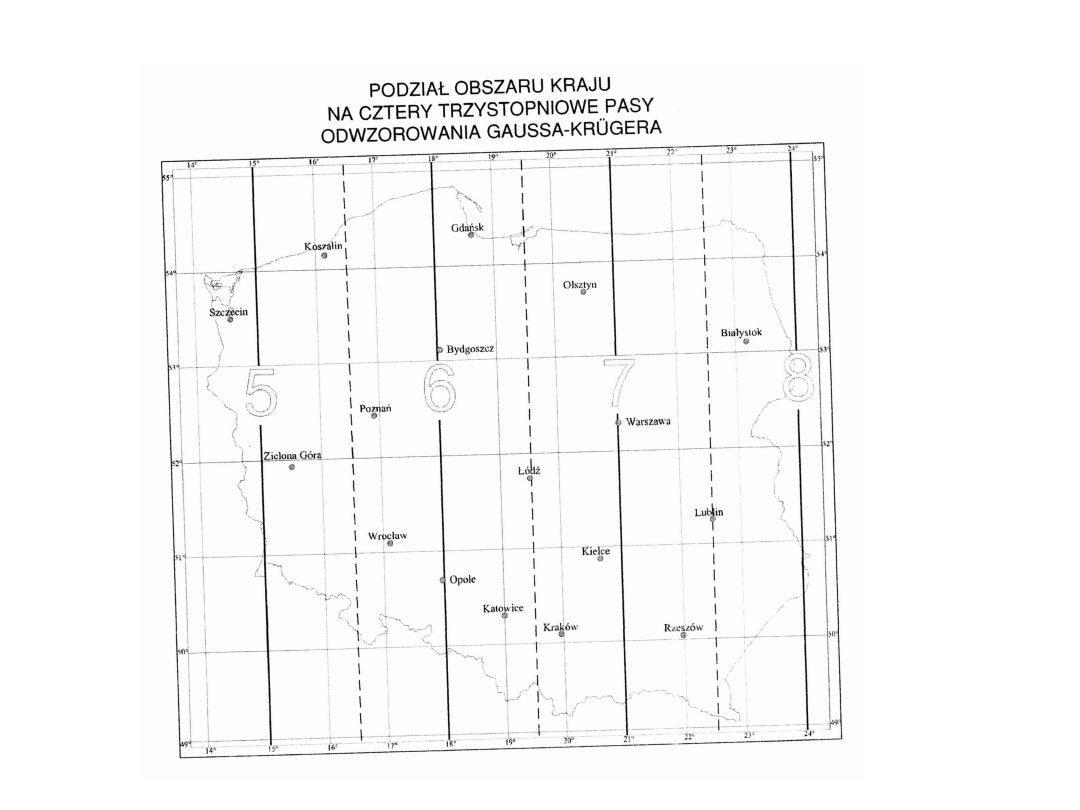
bez dużych zniekształceń, dlatego obszar ziemi dzieli się na
wąskie pasy południkowe i każdy z takich pasów odwzorowuje się
oddzielnie w układzie współrzędnych prostokątnych płaskich.

Układ współrzędnych „1992” i „2000”
 
W Polsce utworzono dwa nowe układy współrzędnych, tzw. układ
1992 i układ 2000.
Oba te układy oparte są na współrzędnych geodezyjnych B i L dla
których powierzchnią odniesienia jest elipsoida GRS 80. Współrzędne
prostokątne obliczone są w odwzorowaniu Gaussa – Krugera.

Układ 1992 stosowany jest przy sporządzaniu mam topograficznych w
skalach 1:10000 i mniejszych
Układ 2000 stosowany jest do sporządzenia map w skalach 1:10000 i
większych.
Obraz równika w tym odwzorowaniu jest linią o równaniu x=0, a
obraz południka osiowego linią o równaniu:

y=5 500 000 m przy południku L

0

=15

o

y=6 500 000 m przy południku L

0

=18

o

y=7 500 000 m przy południku L

0

=21

o

y=8 500 000 m przy południku L

0

=24

o

Pierwsza cyfra współrzędnej Y każdego punktu jest numerem pasa, w
którym leży punkt a jej pomnożenie przez trzy daje długość
geograficzną południka osiowego tego pasa wyrażoną w stopniach.

W układzie 2000 prowadzona jest mapa zasadnicza, którą
wykorzystujemy w pracach projektowych.

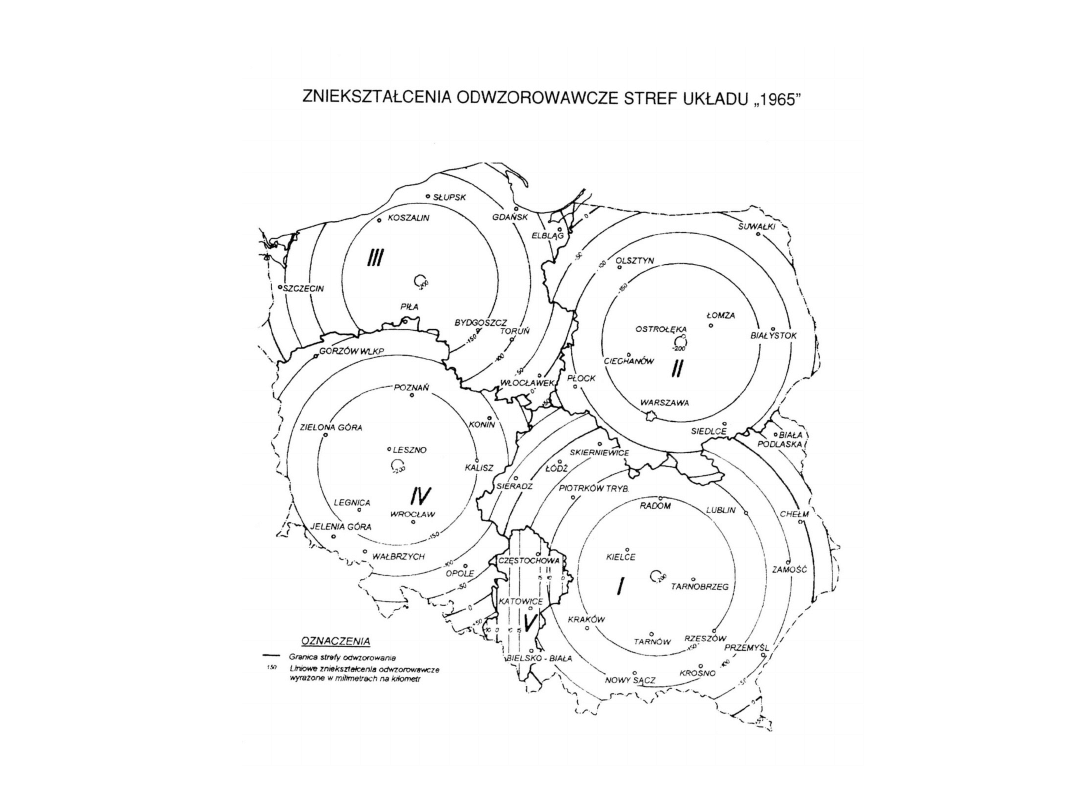
Oprócz wyżej wymienionych układów jest jeszcze stosowany układ,
1965 w którym do niedawna była prowadzona mapa zasadnicza.

Układ 1965 składa się z czterech układów współrzędnych
nazwanych strefami
od I do IV w odwzorowaniu quasi – stereograficznym oraz jednego
układu strefa V
w odwzorowaniu Gaussa – Krugera.

Układ ten może być stosowany do 2009 roku.

Sposób dokonywania przeliczeń między układami „1965” a „2000”
oraz dane do tych operacji zawarte są w instrukcji technicznej nr
G2.