do krakowskiego id 137903

Kret Agnieszka

gr7; 13.12.2011r

Kowalski Kamil

Kozieł Bartosz

Ćwiczenie Nr 4 – „Sporządzanie wykresów zapotrzebowania mocy i momentu zespołu napędowego”

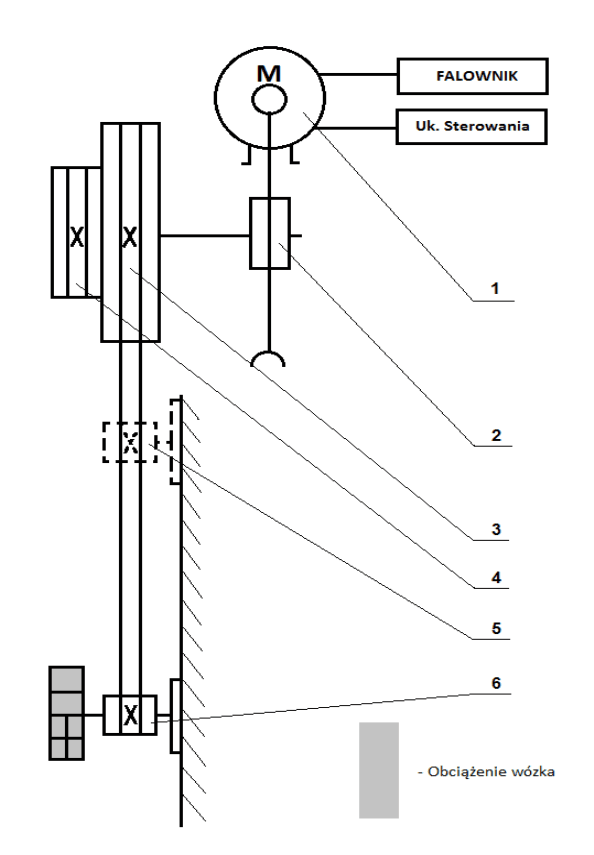
Schemat stanowiska

Silnik

Przekładnia Ślimakowa(i=10,23) 3.

Koło linowo – napędowe Φnd=0,125

Koło linowo – napędowe Φnd=0,075

Wózek nieobciążony wraz z kołem linowym Φnw=0,063

Wózek obciążony wraz z kołem linowym Φnw=0,063

Zadany wykres prędkości jazdy wózka w funkcji drogi v(s)

V[m/s]

0,12

v[m/s] s[m]

0,10

0,00 0,00

0,11 0,20

0,08

0,11 0,55

0,06

v(s)

0,05 0,60

0,04

0,05 0,80

0,02

0,00 1,00

0,00

0,20

0,40

0,60

0,80

1,00

1,20 s[m]

Tabela z parametrami pracy napędu.

Końcowa

prędkość

Końcowa

kątowa

obrotowa

prędkość

silnika

jazdy

Czas

podczas

Etap Pracy

wózka

trwania

etapu

podczas

etapu

pracy –

etapu

pracy

koło

pracy

napędowe

Φnd=0,125 Φnd=0,075 Φnd=0,125 Φnd=0,075

[m]

’

i[m/s]

ti [s]

ωsi [1/s]

nsi [%]

0,11

3,64

36,01

60,02

22,91

38,21

0,11

3,18

36,01

60,02

22,91

38,21

I I

0,05

0,63

16,37

27,28

10,42

17,37

0,05

4,00

16,37

27,28

10,42

17,37

0,00

8,00

Obliczenia

s1 = s0 + v0t + ௔௧మ ; s

ଶ

0 = 0, v0 = 0

మ

s1 = ௔௧మ = ௩಺ ∙ ௧಺ = ௩಺∙௧಺ → ݐ

= 3,64ݏ;

ଶ

௧

ூ = ଶ௦಺

಺

ଶ

௩಺

ݐூூ = ௦మି௦಺ =3,18s;

௩಺

ݐூூூ = ଶ(௦಺಺಺ି௦಺಺) =0,625s;

௩಺ା௩಺಺

ݐூ௏ = ௦಺ೇି௦಺಺಺ =4s;

௩಺಺

ݐ௏ = ଶ(௦ೇି௦಺ೇ) =8s;

௩బା௩಺಺

Czasy od początku ruchu wózka wynoszą odpowiednio: t1 = 3,64s

t2 = tI+tII = 6,82s i analogicznie reszta t3 = 7,44s

t4 = 11,44s

t5 = 19,44s

ωsi = ସ௩ ∙ ݅; ݅ = 10,23

ః೙

ωs1d = 36,01[ଵ]

]

௦

s1m = 60,02[ଵ

௦

ωs2d = 16,37[ଵ]

]

௦

s2m = 27,28[ଵ

௦

nmax = 1500[௢௕௥]

௠௜௡

ns1d = 343,87[௢௕௥] → 22,92% n

] → 38,21% n

௠௜௡

max

ns1m = 573,15[௢௕௥

௠௜௡

max

ns2d = 156,32[௢௕௥] → 10,42% n

] → 17,37% n

௠௜௡

max

ns2m = 260,50[௢௕௥

௠௜௡

max

m = 3,56kg – masa wózka

M = 4,88kg – masa obciążenia

In = 6,64∙10-3[kg∙m2]

Ip = 9∙10-4[kg∙m2]

Iw = 4,44∙10-4[kg∙m2]

i = 10,23

Duże koło:

Obliczenia ε(przyspieszenia) silnika dla odpowiednich przedziałów czasu(do wykresu) ε = ௱ఠ

௱௧

ε1(0 →3,64) = ଷ଺,଴ଵ = 9,89[ ଵ ]

ଷ,଺ସ

௦మ

ε2(6,82→7,44) = ଵ଺,ଷ଻ିଷ଺,଴ଵ = -31,42[ ଵ ]

଴,଺ଶହ

௦మ

ε3(11,44 → 19,44) = ଴ିଵ଺,ଷ଻ =-2,05[ ଵ ]

଼

௦మ

Mst = ቀሺ௠ାெሻ௚ ∙ థ೙೏ − ௠௚ ∙ థ೙೏ቁ ∙ ଵ = ቀெ௚థ೙೏ቁ ∙ ଵ = 0,146224[ܰ݉]

ଶ

௜

ସ

௜

Md = Izr௱ఠ

௱௧

M = Mst + Md

ଵ I 2 = σ ଵ݉ ଶ + σ ଵܫ ଶ /∙ 2

ଶ zrωs

ଶ

௜ݒ௜

ଶ ௜ω௜

ଶ

௭௥ω௦ = ܯ(ݒ ∙ )ଶ + ܫ

)ଶ + ܫ

+ I

/ω

௡(ω௦ ∙ ݅

௣ωୱ

୵ω୵

ୱ

మ

ଵ

థ೙೏

௭௥ = ܫ௣ + ܫ௡

+ ܯ ଵ

+ 2I

∙ థ೙೏ ; ݒ = ߱ݎ → ߱ థ೙೏; ߱

∙ ߱

௜మ

௜మ ସ

୵ ∙ ଵ௜ ସ∙థమ

௪ = ௥

௡ௗ = థ೙೏

௡ௗ

ೢ

ଶ

ଶோ

ଶ∙థೢ

଴,ଵଶହమ

௭௥ = 0,0009 + 0,00664

ଵ

+ 4,88 ଵ

+ 2 ∙ 0,00044 ∙ ଵ ∙ ሺ଴,ଵଶହሻమ =

ଵ଴,ଶଷమ

ସ

ଵ଴,ଶଷ ସ∙ሺ଴,଴଺ଷሻమ

= 0,00123[݇݃ ∙ ݉ଶ]

Md(0 → 3,64s) = ܫ௭௥ ∙ ߝଵ = 0,001145 ∙9,89 = 0,0122

N= M ∙ ωs (np. dla t

=3,64→

0,158424 ∙36,1) =

5,72[W]

N = (0s) N(19,44s)=0

Md(0 → 3,64s) = 0,0122

M = 0,158424[Nm] N (3,64) = 5,72[W]

Md(3,64 → 6,82s) = 0

M = 0,146224[Nm] N (6,82) = 5,28[W]

Md(6,82 → 7,44s) = -0,0386

M = 0,107624[Nm] N (7,44) = 1,76[W]

Md(7,44 → 11,44s) = 0

M = 0,146224[Nm] N (11,44) = 2,39[W]

Md(11,44 → 19,44s) = -0,0025

M = 0,143724[Nm] N (19,44) = 0[W]

Małe koło:

Obliczenia ε(przyspieszenia) silnika dla odpowiednich przedziałów czasu(do wykresu) ε = ௱ఠ

௱௧

ε1(0 →3,64) = ଺଴,଴ଶ = 16,51[ ଵ ]

ଷ,଺ସ

௦మ

ε2(6,82→7,44) = ଶ଻,ଶ଼ି଺଴,଴ଶ = -52,384[ ଵ ]

଴,଺ଶହ

௦మ

ε3(11,44 → 19,44) = ଶ଻,ଶ଼ = -3,41[ ଵ ]

଼

௦మ

Mst = ቀሺ௠ାெሻ௚ ∙ థ೙೘ − ௠௚ ∙ థ೙೘ቁ ∙ ଵ = ቀெ௚థ೙೘ቁ ∙ ଵ = 0,088[ܰ݉]

ଶ

௜

ସ

௜

Md = Izr௱ఠ

௱௧

M = Mst + Md

ଵ I 2 = σ ଵ݉ ଶ + σ ଵܫ ଶ /∙ 2

ଶ zrωs

ଶ

௜ݒ௜

ଶ ௜ω௜

ଶ

௭௥ω௦ = ܯ(ݒ ∙ )ଶ + ܫ

)ଶ + ܫ

+ I

/ω

௡(ω௦ ∙ ݅

௣ωୱ

୵ω୵

ୱ

మ

ଵ

థ೙೘

௭௥ = ܫ௣ + ܫ௡

+ ܯ ଵ

+ 2I

∙ థ೙೘ ; ݒ = ߱ݎ → ߱ థ೙೘; ߱

∙ ߱

௜మ

௜మ ସ

୵ ∙ ଵ௜ ସ∙థమ

௪ = ௥

௡௠ = థ೙೘

௡௠

ೢ

ଶ

ଶோ

ଶ∙థೢ

଴,଴଻ହమ

௭௥ = 0,0009 + 0,00664

ଵ

+ 4,88 ଵ

+ 2 ∙ 0,00044 ∙ ଵ ∙ ሺ଴,଴଻ହሻమ =

ଵ଴,ଶଷమ

ସ

ଵ଴,ଶଷ ସ∙ሺ଴,଴଺ଷሻమ

= 0,00106[݇݃ ∙ ݉ଶ]

Md(0 → 3,64s) = ܫ௭௥ ∙ ߝଵ = 0,00106 ∙16,51 = 0,0175

N = M ∙ ωs (np. dla t =3,64→

0,1055 ∙ 60,02) = 6,33

N(0s) i N(19,44s) =0

Md(0 → 3,64s) = 0,0175

M = 0,1055[Nm]

N(3,64) = 6,33[W]

Md(3,64 → 6,82s) = 0

M = 0,0880[Nm]

N(6,82) = 5,28[W]

Md(6,82 → 7,44s) = -0,0555

M = 0,0325[Nm]

N(7,44) = 0,89[W]

Md(7,44 → 11,44s) = 0

M = 0,0880 [Nm]

N(11,44) = 2,40[W]

Md(11,44 → 19,44s) = -0,0036

M = 0,0844, [Nm]

N(19,44) = 0[W]

Wykresy na podstawie obliczeń powyżej: Duże Koło:

n(t)

400

n sil

[obr/min]

czas[s]

350

300

343,87

250

3,64

343,87

200

6,82

w(t)

150

156,32

7,44

100

156,32

11,44

19,44

ε(t)

Przys. ε[ ଵ ]

௦మ

Czas[s]

9,89

3,64

6,82

-5 0

-31,42

6,82

-10

-31,42

7,44

e(t)

-15

7,44

-20

11,44

-25

-2,05

11,44

-30

-2,05

19,44

-35

19,44

Moment[Nm] Czas[s]

M(t)

0,146224

0,17

0,158424

0,16

0,158424

3,64

0,15

0,146224

3,64

0,146224

6,82

0,14

0,107624

6,82

0,13

M(t)

0,107624

7,44

0,12

0,146224

7,44

0,146224

11,44

0,11

0,143724

11,44

0,1

0,143724

19,44

0,146224

19,44

N(t)

Moc[W]

Czas[s]

5,72

3,64

5,28

6,82

1,76

7,44

N(t)

2,39

11,44

19,44

Małe Koło:

n(t)

700

n sil

600

[Obr/min]

Czas[s]

500

400

573,15

3,64

573,15

6,82

300

n(t)

260,50

7,44

200

260,50

11,44

19,44

100

ε(t)

Przys.

ε[ ଵ ]

௦మ

Czas[s]

16,51

3,64

-10 0

6,82

-20

e(t)

-52,38

6,82

-30

-52,38

7,44

-40

11,44

-50

-3,41

11,44

-60

-3,41

19,44

Moment[Nm] Czas[s]

M(t)

0,898

0,11

0,915

0,1

0,915

3,64

0,09

0,898

3,64

0,898

6,88

0,08

0,8441

6,88

0,07

0,8441

7,44

0,06

M(t)

0,898

7,44

0,05

0,898

11,44

0,04

0,8945

11,44

0,03

0,8945

19,44

0,898

19,44

N(t)

Moc[W]

Czas[s]

6,33

3,64

5,28

6,88

0,89

7,44

N(t)

2,40

11,44

19,44

Wykresy uzyskane na drodze doświadczalnej: Duże Koło:

400

300

200

100

Prędkość

Prędkość zadana

Przyspieszenie silnika

-100

-200

-300

Czas [s]

N(t)

oc [W]

Moc

-1

Czas [s]

Małe Koło:

700

600

500

400

300

200

Prędkość

100

Prędkość zadana

Przyspieszenie silnika

-100

-200

-300

-400

Czas[ s]

N(t)

oc [W]

Moc

-1

Czas [s]

Wnioski:

Wykresy sporządzone obliczeniowo w przybliżeniu pokrywają się z wykresami rzeczywistymi wykonanymi na podstawie pomiarów, przez co możemy je traktować jako poglądowe przedstawiające ogólną skalę badanej wielkości.

Na rzeczywistych wykresach mocy widać ze dla dużego koła moc potrzebna do uzyskania danej prędkości ruchu wózka jest mniejsza niż dal małego koła, czego nie można zauważyć na wykresach obliczeniowych, gdzie maxymalne wartości mocy praktycznie się pokrywają.

Najgwałtowniejsze zmiany następują przy zmianie prędkości. Na obu wykresach zaobserwować możne że po osiągnięciu danej prędkości wykres stabilizuje się, ponieważ moc silnika w chwili osiągnięcia danej prędkości była np. dla zwiększania prędkości nieco wyższa od mocy potrzebnej do pracy z określoną prędkością.

Układ przedstawiony na schemacie zawsze posiada swój moment statyczny wynikający z obciążenia układu. Aby wprawić go w ruch potrzebujemy momentu dynamicznego, który zapewnia nam silnik. Moment całkowity jest sumą momenty statycznego i dynamicznego.

Moment dynamiczny wynosi 0 gdy układ spoczywa lub porusza się ruchem jednostajnym.