62. Polimorfizm statyczny – szablony.
W C++ wprowadzono nowy mechanizm: szablony. Szablony zezwalają na definiowanie całych rodzin funkcji, które następnie mogą być używane dla różnych typów argumentów.
Weźmy pod uwagę definicję funkcji:
int max(int a, int b) {return (a>b)?a:b;};
double max(double a,double b) {return (a>b)?a:b;};
string max(string a,string b) {return (a>b)?a:b;};
Definicja szablonu funkcji max, odpowiadającej powyższej definicji wygląda następująco: template<typename T> T max(T a,T b) {return (a>b)?a:b;};
Wyrażenie template<typename T> oznacza, że mamy do czynienia z szablonem, który posiada jeden parametr formalny nazwany T. Słowo kluczowe typename oznacza, że parametr ten jest typem (nazwą typu). Zamiast słowa typename możemy użyć słowa kluczowego class. Nazwa tego parametru może być następnie wykorzystywana w definicji funkcji w miejscach, gdzie spodziewamy się nazwy typu. I tak powyższe wyrażenie definiuje funkcję max, która przyjmuje dwa argumenty typu T i zwraca wartość typu T, będącą wartością większego z dwu argumentów.
Typ T jest na razie niewyspecyfikowany. W tym sensie szablon definiuje całą rodzinę funkcji.
Konkretną funkcję z tej rodziny wybieramy poprzez podstawienie za formalny parametr T
konkretnego typu będącego argumentem szablonu. Takie podstawienie nazywamy konkretyzacją szablonu. Argument szablonu umieszczamy w nawiasach ostrych za nazwą szablonu: int i,j,k;
k=max<int>(i,j);
Dedukcja argumentów szablonu
Użyteczność szablonów funkcji zwiększa istotnie fakt, że argumenty szablonu nie muszą być podawane jawnie. Kompilator może je wydedukować z argumentów funkcji. Tak więc zamiast int i,j,k;
k=max<int>(i,j);
możemy napisać
int i,j,k;
k=max(i,j);
i kompilator zauważy, że tylko podstawienie int-a za T umożliwi dopasowanie sygnatury funkcji do parametrów jej wywołania i automatycznie dokona odpowiedniej konkretyzacji.
Może się zdarzyć, że podamy takie argumenty funkcji, że dopasowanie argumentów wzorca będzie niemożliwe, otrzymamy wtedy błąd kompilacji. Trzeba pamiętać, że mechanizm automatycznego dopasowywania argumentów szablonu powoduje wyłączenie automatycznej konwersji argumentów funkcji. Podanie jawnie argumentów szablonu (w nawiasach ostrych za nazwą szablonu) jednoznacznie określa sygnaturę funkcji, a więc umożliwia automatyczną konwersję typów.
Ilustruje to poniższy kod:
template<typename T> T max(T a,T b) {return (a>b)?a:b;}
main() {
// błąd: kompilator nie jest w stanie wydedukowac argumentu szablonu, bo typy
// argumentów (double,int) nie pasują do (T,T)
cout<<::max<int>(3.14,2)<<endl;
// podając argument jawnie wymuszamy sygnaturę int max(int,int), a co za tym
// idzie automatyczną konwersję argumentu 1 do int-a
cout<<::max<double>(3.14,2)<<endl;
// podając argument szablonu jawnie wymuszamy sygnaturę
// double max(double,double)
// a co za tym idzie automatyczną konwersję argumentu 2 do double-a int i;
cout<<::max<int *>(&i,i)<<endl;
//błąd: nie istnieje konwersja z typu int na int*
Szablony metod
C++ umożliwia również definiowanie szablonów metod klasy np.:
struct Max {
template<typename T> T max(T a,T b) {return (a>b)?a:b;}
};
main() {
Max m;
m.max(1,2);
}
Szablonów metod składowych dotyczą takie same reguły jak szablonów funkcji.
Szablony klas
Jako przykład weźmy sobie stos liczb całkowitych. Możliwa definicja klasy stos może wyglądać następująco:
class Stack {
private:
int rep[N];
size_t top;
public:
static const size_t N=100;
Stack():_top(0) {};
void push(int val) {_rep[_top++]=val;}
int pop() {return rep[--top];}
bool is_empty {return (top==0);}
}
Ewidentnie ten kod będzie identyczny dla stosu obiektów dowolnego innego typu, pod warunkiem, że typ ten posiada zdefiniowany operator=() i konstruktor kopiujący.
Rozwiązaniem są znów szablony, tym razem szablony klas. Podobnie jak w przypadku szablonów funkcji, szablon klasy definiuje nam w rzeczywistości całą rodzinę klas. Szablon klasy Stack możemy zapisać następująco:
template<typename T> class Stack {
public:
static const size_t N=100;
T _rep[N];
size_t _top;
public:
Stack():_top(0) {};
void push(T val) {_rep[_top++]=val;}
T pop() {return _rep[--_top];}
bool is_empty {return (_top==0);}
};
Tak zdefiniowanego szablonu możemy używać podając jawnie jego argumenty.
Stack<string> st;
st.push("ania");
st.push("asia");
st.push("basia");
while(!st.is_empty() ){
cout<<st.pop()<<endl;
}
Polimorfizm statyczny
Jednym z głównych paradygmatów programowania obiektowego jest polimorfizm. Spójrzmy na poniższy przykład kodu:
class Shape {
protected:
long int _x;
long int _y;
public:
Shape(long x,long y):_x(x),_y(y){};
long get_x() const {return _x;}
long get_y() const {return _y;}
virtual void draw() = 0;
virtual ~Shape() {};
};
Klasa ta stanowić będzie klasę bazową dla wszystkich klas opisujących kształty. Klasa Shape jest klasą abstrakcyjną, ponieważ zawiera niezaimplementowaną wirtualną czystą fukcję void draw(). Kod definiujący konkretne klasy kształtów może wyglądać następująco: class Circle: public Shape {
protected:
long _r;
public:
Circle(long x, long y,long r) :Shape(x,y), _r(r) {}
virtual void draw() {
std::cerr<<"Circle : "<<_x<<" "<<_y<<" : "<<_r<<std::endl;
}
long get_r() const {return _r;};
};
A to funkcja odświeżająca ekran:
void draw_shapes(Shape *table[],size_t n) {
for(size_t i=0;i<n;++i)
table[i]->draw();
}
Funkcja draw_shapes wykorzystuje zachowanie polimorficzne: to która funkcja draw zostanie wywołana zależy od tego jaki konkretny kształt jest wskazywany przez element tablicy. Łatwo się o tym przekonać wykonując np. następujący kod:
int main() {
Shape *list[4];
list[0]=new Circle(0,0,100);
list[2]=new Circle(10,10,100);
draw_shapes(list,2);
}
Jest to polimorfizm dynamiczny, czyli możliwość decydowania o tym jaka funkcja zostanie wywołana pod daną nazwą nie w momencie kompilacji (czyli pisania kodu), ale w samym momencie wywołania.
Patrząc na kod funkcji draw_shapes możemy zauważyć, że korzysta on jedynie z własności posiadania przez wskazywane obiekty metody draw(). To sygnatura, czyli typ parametru wywołania tej funkcji określa, że musi to być wskaźnik na typ Shape. Możemy zrezygnować z wymuszania typu argumentu wywołania funkcji poprzez użycie szablonu funkcji: template<typename T> void draw_template(T table[],size_t n) {
for(size_t i=0;i<n;++i)
table[i].draw();
}
Taką funkcję możemy wywołać dla dowolnej tablicy, byle tylko przechowywany typ posiadał
metodę draw. Może to być obiekt typu Circle (nie Shape, obiekty klasy Shape nie istnieją!), ale też inne zupełnie z nimi nie związane. Ilustruje to poniższy przykład: class Drawable {
public:
void draw() {cerr<<"hello world!"<<endl;}
};
int main() {
Drawable table_d[1]={Drawable()};
Circle table_c[2]={Circle(10,10),Circle(0,50)};
draw_template(table_d,1);
draw_template(table_c,2);
}
Jest to polimorfizm statyczny: to kompilator zadecyduje na podstawie typu tablicy jaką funkcję draw wywołać.
63. Tablice i rekordy oraz ich zastosowania.
Tablica w prawie wszystkich komputerach stanowi bezpośrednie odwzorowanie pamięci i jest prymitywem w większości języków programowania. Tablica jest
• sztywnym zbiorem danych tego samego typu,
• zapisanych w jednym ciągu
• i dostępnych za pośrednictwem indeksu - do i-tego elementu tablicy a można się odwołać za pomocą konstrukcji a[i].
W C++ odpowiedzialność za sens danych w tablicy spoczywa na programiście. Również programista musi dbać o to, by użyć właściwej wartości indeksu: nieujemnego i mniejszego niż rozmiar tablicy. W Pascalu zakres indeksów tablicy jest dowolny, ale nie może przekraczać zakresu dozwolonego dla liczb całkowitych.
Są też tablice wielowymiarowe, które są już typem złożonym i w rzeczywistości w C++ są zapisane sekwencyjnie w tablicy jednowymiarowej na zasadzie starszeństwa wierszy.
Zalety tablicy to szybki dostęp do każdego elementu oraz możliwość interpretacji i manipulacji liczbowym indeksem, a wadą stały rozmiar. Typowe i uzasadnione wykorzystanie tablicy występuje w algorytmie „Sito Eratostenesa”. Poniżej jego przykładowa implementacja.
#include <iostream.h>
static const int n = 1000;
int main()
{
int i, a[n];
for (i = 2; i < n; i++)
a[i] = 1; //Liczba pierwsza będzie oznaczona przez 1.
for (i = 2; i < n; i++) //Dla każdej liczby 'i'
if ( a[i] ) //jeszcze nie sprawdzonej,
for (int j = i; j*i < n; j++) //liczby podzielne przez 'i'
a[i*j] = 0; //oznaczamy jako nie pierwsze – tu
wykorzystujemy właściwość tablicy tj. szybki dostęp i manipulacja indeksem.
for (i = 2; i < n; i++)
if (a[i])
cout << " " << i << endl; //Wyświetlamy liczby pierwsze.
}
Tablicę wykorzystuje się jako agregat typów wbudowanych (np. tablica znaków jako napis, tablica „intów” jako pewien zbiór liczb całkowitych) lub do realizacji bardziej abstrakcyjnych typów danych np. lista jednokierunkowa.
Rekordy służą do przechowywania powiązanych ze sobą danych, ale różnych typów (heterogenicznych). Na przykład opis człowieka może zawierać nazwisko i imię (typ tekstowy o stałej długości 20 i 10 znaków), płeć (np. typ znakowy), wiek (typ liczbowy całkowity), wzrost (typ rzeczywisty) itd. W tablicy nie można przechowywać elementów różnych typów - umożliwia to tylko rekord.
Cechy rekordu to:
• elementy rekordu to pola;
• każde pole może być dowolnego typu (podstawowego, prymitywnego, prostego) np. int, int tab[4];
• każde pole musi być podane jawnie (tzn. musi zostać zadeklarowane);
• kolejność pól w deklaracji jest nieistotna.
Przykład definicji rekordu:
Tosoba = RECORD
nazwisko:string[20];
imie:string[10];
plec:char;
wiek:byte;
wzrost:real;
end;
Do tak zdefiniowanego typy danych można utworzyć zmienne, w których można przechowywać jednocześnie kilka informacji opisanych w rekordzie.
var osoba1,osoba2:Tosoba;
Przypisanie danych do takiej zmiennej będzie wyglądało w następujący sposób: osoba1.nazwisko:=’Libront;
osoba1.wiek:=35;
osoba2.wiek:=osoba1.wiek+2;
Rekord wykorzystuje się jako typ danych przechowujący informacje niejednolite z punktu widzenia typów podstawowych, ale za to zrozumiały dla człowieka. Np. z punktu widzenia typów podstawowych i wydajności, struktura odpowiadająca karcie katalogowej w bibliotece powinna w Pascalu wyglądać tak:
var
Tytul : array[1..750] of string[30];
Autor : array[1..750] of string[25];
Wypozyczajacy : array[1..750] of string[25];
Licznik : array[1..750] of word;
Natomiast z punktu widzenia człowieka tak:
var
Ksiazka : record
Tytul : string[30];
Autor : string[25];
Wypozyczajacy : string[25];
Licznik : word
end;
Rekord po dodaniu pola/pól typu wskaźnikowego (pointer) staje się podstawą typów bardziej skomplikowanych pozwalając tworzyć abstrakcyjne struktury danych potrzebne do rozwiązywania trudnych zagadnień.
64. Listy i drzewa oraz ich zastosowania. Stosy i kolejki.
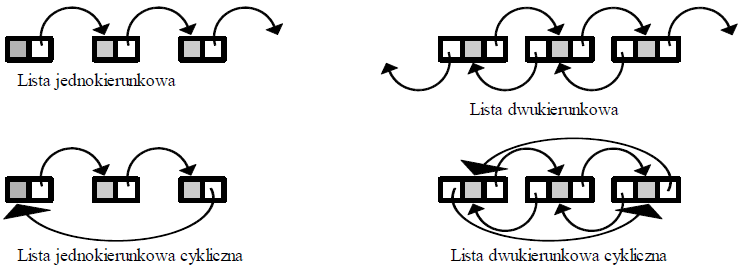
Definicja listy połączonej (jednokierunkowej): jest to zbiór elementów, z których każdy jest zawarty w węźle, zawierającym dodatkowo łącze do innego węzła. Zatem lista to węzły, które koniec końców są ze sobą połączone łączami. Ze względu na skierowanie tych połączeń względem innych węzłów wyróżniamy w szczególności listę jedno- i dwukierunkową (podwójnie połączoną).
Poniżej wizualizacja – szare pola to wartości elementów, a białe to łącza.
Podstawowe operacje na liście to:
• zwracanie wartości elementu,
• zwracanie wartości elementu, do którego prowadzi łączę od obecnego elementu,
• dodawanie nowego elementu,
• usuwanie elementu (przy tej operacji, w c++, trzeba operować łączami tak by nie doszło do
„wycieku pamięci”).
Bardziej złożone to: wstawianie z sortowaniem i sortowanie. Cechą i zaletą listy jest łatwa zmiana kolejności jej węzłów, ale kosztem czasu dostępu – żeby dostać się do elementu trzeba przejść od początku przez wszystkie węzły poprzedzające. Dostęp do elementów jest zapewniony za pośrednictwem innych węzłów. Stąd druga nazwa listy - struktura autoreferencyjna. Listy wykorzystuje się gdy często zmienia się liczba elementów lub ich kolejność, ponieważ koszty
„przesunięcia”, usunięcia lub dodania węzła są stałe i małe. Często stosuje się węzły atrapy. W
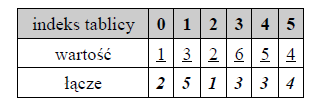
przypadku listy jednokierunkowej mamy jeden taki węzeł zwany głową (head) wskazujący na początek listy. Dla dwukierunkowej listy potrzebne są dwa węzły zwane głową i ogonem (tail) wskazujące odpowiednio początek i koniec listy. W przypadku c++ węzłami atrapami są najczęściej wskaźniki. Lista jednokierunkowa zrealizowana przy pomocy tablicy i rekordu (rzadko stosowane) wyglądała by następująco:
Czyli kolejne elementy listy (indeks 0 to początek) mają następujące indeksy z łączami (0,2) > (2,1)
> (1,5) > (5,4) > (4,3) > (3,3), a wartości tej listy to odpowiednio 1 > 2 > 3 > 4 > 5 > 6. Ostatnie
„wskazanie” na samego siebie (3,3) oznacza koniec listy. W przypadku listy cyklicznej 3
wskazywałoby na 0 tj. (3,1).
Poniżej przykładowa implementacja listy jednokierunkowej z użyciem tablicy:
#include <iostream>
using namespace std;
struct record
{
int value;
int next;
};
int main()
{
record tab[6];
tab[0].value=1; tab[1].value=3; tab[2].value=2;
tab[3].value=6; tab[4].value=5; tab[5].value=4;
tab[0].next=2; tab[1].next=5; tab[2].next=1;
tab[3].next=3; tab[4].next=3; tab[5].next=4;
int i=0; //poczatek listy - moze byc w innym
miejscu.
while(tab[i].next!=i)
{
cout<<tab[i].value<<" ";
i=tab[i].next; //wypisze na ekran 1 2 3 4 5 6.
}
getchar();
return 0;
}
A tutaj implementacja listy jednokierunkowej z użyciem samych rekordów:
#include <iostream>
using namespace std;
struct record {
int value;
record* next;
};
void add(record*& head, const int value) {
if(head==NULL)
{
head=new record;
head->value=value;
head->next=NULL;
}
else
{
record* iter=head;
while(iter->next!=NULL) iter=iter->next;
iter->next=new record;
iter->next->value=value;
iter->next->next=NULL;
}
}
int main()
{
record* list=NULL;
add(list,1); add(list,2); add(list,3);
add(list,4); add(list,5); add(list,6);
record* iter=list;
while(iter!=NULL)
{
cout<<iter->value<<" ";
iter=iter->next;
}
getchar();
return 0;
}
Drzewo
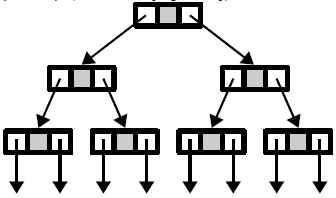
Definicja drzewa (tree): jest to graf spójny i acykliczny (wizualizacja poniżej).
O drzewie mówimy w przypadku:
• jawnego drzewa (dosłownego), mając na myśli drzewiasty układ rekordów jak na rysunku powyżej
• warstwy abstrakcji mając na myśli strukturę matematyczną.
Odpowiada to niskiemu i najwyższemu poziomowi abstrakcji. W tym miejscu będziemy mówić o drzewach jako strukturach, które implementuje się przez drzewiasty układ rekordów lub tablicę.
Oczywiście jest też drzewo będące szczególnym przypadkiem grafu. Ale graf z kolei, nawet gdy spełnia warunki drzewa, ma inną reprezentację (macierz sąsiedztwa, tablica list, lista krawędzi).
Inna reprezentacja daje inne możliwości i przez to inne zastosowania. Podkreślam jeszcze raz, że w tym miejscu mówimy tylko o drzewach, których implementacja to drzewo rekordów lub tablica.
Wyróżniamy typy drzew:
1. z korzeniem – wyróżniony jest dokładnie jeden wierzchołek;
2. uporządkowane – ma korzeń, a kolejność dzieci każdego węzła jest ściśle określona; 3. m-drzewo – jest uporządkowane i każdy węzęł ma określoną liczbę dzieci; Najczęściej stosowanym przypadkiem m-drzewa jest drzewo binarne. Jego cechą jest to, że każdy wierzchołek ma nie więcej niż dwoje dzieci. Wyróżniamy odmiany drzewa binarnego:
a) drzewo regularne - liczba dzieci każdego wierzchołka wynosi dokładnie 0 albo 2.
b) binarne drzewo przeszukiwań (Binary Search Tree) – w każdym z węzłów drzewa BST przechowywany jest unikatowy klucz. Wartość klucza jest zawsze większa niż wartości wszystkich kluczy z lewego poddrzewa, a mniejsza niż wartości wszystkich kluczy z prawego poddrzewa (relacja może być odwrócona - to kwestia umowy); przechodząc rekurencyjnie drzewo metodą inorder (lewe dziecko, rodzic, prawe dziecko) uzyskuje się ciąg wartości posortowanych rosnąco.
Wadą tego drzewa jest to, że trzeba je często wyważać. Natomiast zaletą przy wyważonym BST jest szybkie wyszukiwanie.
c) AVL – drzewo BST, w którym każdy wierzchołek ma przypisany stopień wyważenia (o wartościach ze zbioru {-1, 0, 1}) zmieniany przy każdej operacji na drzewie. Jeżeli po
dodaniu nowego węzła współczynnik wyważenia ma nieprawidłową wartość, to następuje wyważenie drzewa przez rotację węzłów.
d) Kopiec (heap) zupełny – drzewo regularne, w którym liście występują na ostatnim i ewenetualnie na przedostatnim poziomie; przy czym w ostatnim poziomie liście są spójnie ułożone od lewej do prawej. Ten ADT można zaimplementować przez drzewo rekordów, ale również przez tablicę. Wówczas w tablicy lewe dziecko węzła o indeksie n ma indeks 2n, a prawe 2n+1. Automatycznie rodzic węzła o indeksie n ma indeks n mod 2 niezależnie od tego czy jest lewym czy prawym dzieckiem.
4. b-drzewo – każdy węzeł zawiera węzły wewnętrzne. Węzeł może mieć dowolną liczbę dzieci. Węzły dzieci wychodzą od węzłów wewnętrznych. Ten typ drzewa ma zastosowanie w bazach danych, gdyż nie wymaga częstego wyważania.
Zastosowania drzew są bardzo szerokie:
• sztuczna inteligencja – drzewo gry mini-max w algorytmie mini-max,
• systemy podejmowania decyzji - drzewo decyzyjne,
• grafika komputerowa - drzewo zachodzących na siebie obiektów na scenie,
• symulacja fizyki - drzewo kolizji obiektów na scenie,
• programowanie dynamiczne – drzewo wywołań rekurencyjnych funkcji,
• bazy danych – b-drzewo z danymi łatwo przeszukiwać
• słowniki – drzewo AVL
Stos
Stos to liniowa struktura danych, w której dane dokładane są na wierzch stosu i z wierzchołka stosu są pobierane (bufor typu LIFO, Last In, First Out; ostatni na wejściu, pierwszy na wyjściu). Ideę stosu danych można zilustrować jako stos położonych jedna na drugiej książek – nowy egzemplarz kładzie się na wierzch stosu i z wierzchu stosu zdejmuje się kolejne egzemplarze. Elementy stosu poniżej wierzchołka stosu można wyłącznie obejrzeć, aby je ściągnąć, trzeba najpierw po kolei ściągnąć to, co jest nad nimi.
Stos jest stosowany w systemach komputerowych na wszystkich poziomach funkcjonowania systemów informatycznych, używane są przez procesory do chwilowego zapamiętywania rejestrów procesora, do przechowywania zmiennych lokalnych, a także w programowaniu wysokopoziomowym.
Podstawowe operacje jakie można wykonać na stosie, to:
• push(obiekt) – czyli odłożenie obiektu na stos;
• pop() – ściągnięcie obiektu ze stosu i zwrócenie jego wartości;
• isEmpty() - sprawdzenie czy na stosie znajdują się już jakieś obiekty.
Strukturami danych służącymi do reprezentacji stosu mogą być tablice (gdy znamy maksymalny rozmiar stosu), tablice dynamiczne lub listy. Złożoność obliczeniowa operacji na stosie zależy od konkretnej implementacji, ale w większości przypadków jest to czas stały O(1).
#define STOS_MAX 10 // stos 10-elementowy
int stos[STOS_MAX];
szczyt=0;
push(element) {
if(szczyt < STOS_MAX) {
/* wrzuć na stos */
stos[szczyt] = element;
szczyt++;
else {
/* stos jest już pełny */
...
}
}
pop() {
if(szczyt != 0) {
/* zdejmij ze stosu */
szczyt--;
return stos[szczyt];
}
else {
/* stos jest już pusty */
...
}
}
Kolejka
Kolejka to liniowa struktura danych, w której nowe dane dopisywane są na końcu kolejki, a z początku kolejki pobierane są dane do dalszego przetwarzania (bufor typu FIFO, First In, First Out; pierwszy na wejściu, pierwszy na wyjściu).
Specjalną modyfikacją kolejki jest kolejka priorytetowa – każda ze znajdujących się w niej danych dodatkowo ma przypisany priorytet, który modyfikuje kolejność późniejszego wykonania.
Oznacza to, że pierwsze na wyjściu niekoniecznie pojawią się te dane, które w kolejce oczekują najdłużej, lecz te o największym priorytecie.
Kolejkę spotyka się przede wszystkim w sytuacjach związanych z różnego rodzaju obsługą zdarzeń.
W szczególności w systemach operacyjnych ma zastosowanie kolejka priorytetowa, przydzielająca zasoby sprzętowe uruchomionym procesom.
Przeciwieństwem kolejki jest stos, bufor typu LIFO (ang. Last In, First Out; ostatni na wejściu, pierwszy na wyjściu), w którym jako pierwsze obsługiwane są dane wprowadzone jako ostatnie.
Wyszukiwarka
Podobne podstrony:
62 63 64
61,62,63,64
62 63 407 pol ed02 2005
abc 62 63 Satin
62 63
62, 63
63 64 607 pol ed01 2007
ntw 07 2005 str 62 63
62 63 307 POL ED02 2001
62 63
63 64
62 63
62 63 (2)
09 1995 63 64
63 64
62 63
61,62, 63,64doc II, 61
więcej podobnych podstron