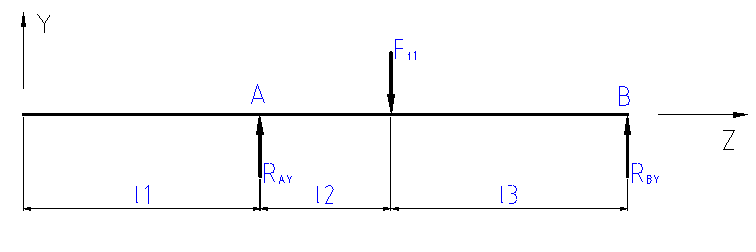
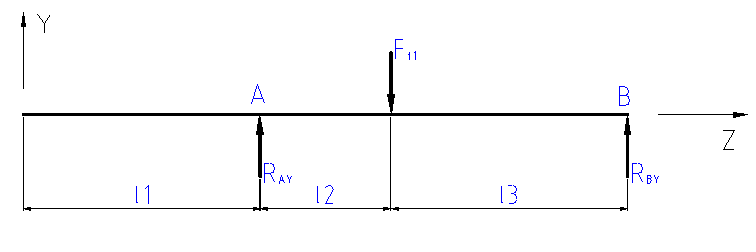
Projekt reduktora dwustopniowego: Schemat reduktora:
Dane:
P := 7.5
[kW]
moc silnika
i :=
przełożenie całkowite reduktora
c
16
n :=
0
1450 [obr/min]
prędkość obrotowa silnika
T := 10000
[h]
liczba godzin pracy reduktora
Przyjmuje material na koła zębate i wałki stal 40HM
i :=
przełożenie na pierwszym stopniu
1
3.15
i :=
przełożenie na drugim stopniu
2
5
Dobieramy liczby zębów na poszczególne koła: z :=
:= ⋅
=
1
24
z2.
z1 i1
z2.
75.6
Przyjmuje liczbę zębów na drugim kole: z :=
2
77
z :=
:= ⋅
=
3
21
z4.
z3 i2
z4.
105
Przyjmuje liczbę zębów na czwartym kole: z :=
4
104
Sprawdzam przełożenie całkowite:
z ⋅
2 z4
i
:=
=
−
=
prz
i
i
0.111< 2%ic
z ⋅
prz
15.889
c
iprz
1 z3
Obliczam obroty na poszczególnych wałkach: 3
n :=
=
×
1
n0
n1
1.45
10 [obr/min]
n :=
=
2
n
[obr/min]
i
2
460.317
1
n2
n :=
=
3
n
[obr/min]
i
3
92.063
2
Obliczam moduł kół zębatych:
ψ := 16
-współczynnik uwzgledniający dokładność kola zębatego (15-25) λ :=
1
0.397
-współczynnik wytrzymałości zęba u podstawy dobrany z tablic λ :=
2
0.375
z
:=
gj
690 [MPa]
x :=
z
2.2
zgj
k
:=
=
go
k
[MPa]
x
go
313.636
z
3
P
m
:=
⋅
12.
267
z ⋅λ ⋅ψ⋅
⋅
1
1
n1 kgo
3
P
m
:=
⋅
34.
267
z ⋅λ ⋅ψ⋅
⋅
3
2
n2 kgo
m
=
Przyjmuję znormalizowany moduł:
:=
12.
1.272
m12
1.25
m
=
Przyjmuję znormalizowany moduł
:=
34.
1.987
:
m34
2
Obliczam poszczególne średnice kół zębatych: y := 1
- współczynnik wysokości zęba
c :=
- współczynnik luzu wierzchołkowego
1
0.25
Średnice koła pierwszego:
d :=
⋅
=
1
m12 z1
d1
30
[mm]
średnica podziałowa kola
d
:=
⋅
=
b1
d1 cos(20deg)
db1
28.191 [mm]
średnica zasadnicza kola
d
:=
+ ⋅ ⋅
=
a1
d1 2 y m12
da1
32.5
[mm]
średnica wierzchołków kola
d
:=
− ⋅( + )⋅
=
f1
d1 2 y c1 m12
df1
26.875
[mm]
średnica podstaw kola
Średnice koła drugiego:
⋅
=
2
m12 z2
d2
96.25
[mm]
d
:=
⋅
=
b2
d2 cos(20deg)
db2
90.445 [mm]
d
:=
+ ⋅ ⋅
=
a2
d2 2 y m12
da2
98.75 [mm]
d
:=
− ⋅( + )⋅
=
f2
d2 2 y c1 m12
df2
93.125 [mm]
Średnice koła trzeciego:
d :=
⋅
=
3
m34 z3
d3
42
[mm]
d
:=
⋅
=
b3
d3 cos(20deg)
db3
39.467 [mm]
d
:=
+ ⋅ ⋅
=
a3
d3 2 y m34
da3
46
[mm]
d
:=
− ⋅( + )⋅
=
f3
d3 2 y c1 m34
df3
37
[mm]
Średnice koła czwartego:
d :=
⋅
=
4
m34 z4
d4
208
[mm]
d
:=
⋅
=
b4
d4 cos(20deg)
db4
195.456 [mm]
d
:=
+ ⋅ ⋅
=
a4
d4 2 y m34
da4
212
[mm]
d
:=
− ⋅( + )⋅
=
f4
d4 2 y c1 m34
df4
203
[mm]
Obliczam momenty obrotowe na poszczególnych wałkach: P
M :=
⋅
=
1
9550
M
[Nm]
n
1
49.397
1
P
M :=
⋅
=
2
9550
M
[Nm]
n
2
155.599
2
P
M :=
⋅
=
3
9550
M
[Nm]
n
3
777.996
3
Obliczam średnice poszczególnych wałków: 3
3
16⋅M⋅10
D :=
M
k
:=
[MPa]
π⋅
so
70
kso
Przyjmuje:
3
3
16⋅M ⋅
1 10
D
:=
=
:=
1.
D1.
15.318
D1
20
[mm]
70⋅π
3
16⋅M ⋅
2 10
D
:=
=
:=
2.
D2.
22.454
D2
30
[mm]
70⋅π
3
3
16⋅M ⋅
3 10
D
:=
=
:=
3.
D3.
38.396
D3
40
[mm]
70⋅π
Obliczam prędkości obwodowe na poszczególnych kołach: π⋅d ⋅
1 n1
V
:=
=
12
V
[m/s]
60000
12
2.278
π⋅d ⋅
4 n3
V
:=
=
34
V
[m/s]
60000
34
1.003
Obliczam siły obwodowe obciążające poszczególne koła: M
3
1
3
F
:= ⋅
⋅
=
×
t1
2 10
F
[N]
d
t1
3.293
10
1
M
3
2
3
F
:= ⋅
⋅
=
×
t2
2 10
F
[N]
d
t2
3.233
10
2
M
3
2
3
F
:= ⋅
⋅
=
×
t3
2 10
F
[N]
d
t3
7.409
10
3
M
3
3
3
F
:= ⋅
⋅
=
×
t4
2 10
F
[N]
d
t4
7.481
10
4
Obliczeniowe siły obwodowe:
C :=
p
1
-współczynnik przeciążenia wg "PKM - Napędy mechaniczne cz.1" tablica 3.1 , str.83
Dla X klasy dokładności koła obliczam Cd: V12
C
:= +
=
d12
1
C
4
d12
1.377
- współczynnik nadwyżek dynamicznych
V34
C
:= +
=
d34
1
C
4
d34
1.25
3
F
:=
⋅ ⋅
=
×
obl1
Ft1 Cp Cd12
Fobl1
4.536
10
[N]
F
:=
⋅ ⋅
=
×
obl2
Ft2 Cp Cd12
Fobl2
4.453
10
[N]
3
F
:=
⋅ ⋅
=
×
obl3
Ft3 Cp Cd34
Fobl3
9.264
10
[N]
3
F
:=
⋅ ⋅
=
×
obl4
Ft4 Cp Cd34
Fobl4
9.353
10
[N]
Obliczanie zębów na naciski według wzorów Hertza: Szerokość kół zębatych:
b
:= ψ⋅
=
12
m12
b12
20 [mm]
b
:= ψ⋅
=
34
m34
b34
32 [mm]
z
:=
H
800
[MPa]
- wg "PKM - Napędy mechaniczne cz.1" rys. 3.3 , str.93
x
:=
ZH
1.38- współczynnik bezpieczeństwa wymagany w obliczeniach zmęczeniowych na naciski 8
C
:=
CH
1 dla 10cykli obciążenia,wg "PKM - Napędy mechaniczne cz.1" tablica 3.11 , str.94
- współczynnik uwzględniający liczbę cykli obciążenia powierzchni zęba C
:=
mα
478.2
- stała uwzględniająca rodzaj materiałów współpracujących kół wg
"PKM - Napędy mechaniczne cz.1" tablica 3.7 , str.89
p
:= π⋅
=
12
m12
p12
3.927
p
:= π⋅
=
34
m34
p34
6.283
Ft1
C :=
=
1
C
b
⋅
1
41.929
12 p12
°E
:=
50
20
12
Ft2
C :=
=
2
C
b
⋅
2
41.167
12 p12
Ft3
C :=
=
3
C
b
⋅
3
36.852
34 p34
°E
:=
50
30
F
34
t4
C :=
=
4
C
b
⋅
4
37.206
34 p34
Współczynnik Co uwzględniający lepkość oleju E50 dobrany w funkcji C wg "PKM -
Napędy mechaniczne cz.1" tablica 3.10 , str.92
C
:=
o.12
1.055
C
:=
o.34
1.116
Wyznaczenie naprężeń dopuszczalnych kH : z ⋅
⋅
H Co.12 CCH
k
:=
=
H12
k
[MPa]
x
H12
611.594
ZH
z ⋅
⋅
H Co.34 CCH
k
:=
=
H34
k
[MPa]
x
H34
646.957
ZH
Obliczam dopuszczalne naprężenia na naciski na kolach: F
σ
obl1
1
:=
⋅
⋅
+
σ
=
Hmax1
Cmα
1
[MPa]
2
Hmax1
275.524
b
⋅
i
12 d1
1
F
σ
obl2
:=
⋅
⋅( + )
σ
=
Hmax2
Cmα
1
i
[MPa]
2
1
Hmax2
151.025
b
⋅
12 d2
F
σ
obl3
1
:=
⋅
⋅
+
σ
=
Hmax3
Cmα
1
[MPa]
2
Hmax3
212.218
b
⋅
i
34 d3
2
F
σ
obl4
:=
⋅
⋅( + )
σ
=
Hmax4
Cmα
1
i
[MPa]
2
2
Hmax4
96.279
b
⋅
34 d4
σ
≤
- warunek został spełniony
Hmax1..2
kH12
σ
≤
- warunek został spełniony
Hmax3..4
kH34
Obliczam odległość osi kół zębatych: a
:=
⋅( + )
:=
1_2
0.5 d1 d2
a1_2.
63
[mm]
a
:=
⋅( + )
=
2_3
0.5 d3 d4
a2_3
125
[mm]
Rozplanowanie wewnętrzne reduktora:
δ := (
⋅
+ ) δ =
.
0.025 a2_3 3
.
6.125
δ := 8
[mm]
- grubość ścianki reduktora
e = 9
[mm]
- minimalna odległość od wewnętrznej ścianki reduktora do bocznej powierzchni obracającej sie.
e :=
1
5
[mm]
- minimalna odległość od wewnętrznej ścianki reduktora do bocznej powierzchni łożyska tocznego.
e :=
2
5
[mm]
-minimalna odległość w kierunku osiowym między obracającymi sie częściami osadzonymi na jednum wale.
e := ⋅
=
3
1 δ
e3
8
[mm]
-minimalna odległość w kierunku osiowym między obracającymi sie częściami osadzonymi na różnych walach.
e :=
4
7
[mm]
-minimalna odległość w kierunku promieniowym między kołem zębatym jednego stopnia a wałem drugiego stopnia.
e :=
⋅
=
5
1.2 δ
e5
9.6
[mm]
-minimalna odległość w kierunku promieniowym od wierzchołków kół zębatych do wewnętrznej scianki korpusu.
e :=
6
10
[mm]
-minimalna odległość w kierunku promieniowym od wierzchołków kół zębatych do dolnej scianki korpusu e :=
7
8
[mm]
- minimalna odległość od bocznych powierzchni części obracających się razem z wałem do nieruchomych części zewnętrznych reduktora.
d
:=
⋅
=
sr2
1.5 δ
dsr2
12
[mm]
- średnica śruby łączącej kołnierz
k := 24
[mm]
- szerokość kołnierza
s := k + δ + 4
s = 36
[mm]
- szerokość kołnierzy łączonych śrubą z uwzględnieniem grubości ścianki
h :=
1
8
[mm]
- grubość kołnierza pokrywy bocznej
h := 0.8⋅h
:=
1
h
7
[mm]
- wysokość łba śruby
L :=
⋅
=
p
1.8 D1
Lp
36
[mm]
- długośc piasty sprzęgła
Lp :=
⋅
=
2
1.6 D2
Lp2
48
[mm]
- długośc piasty koła drugiego
Lp :=
⋅
=
4
1.6 D3
Lp4
64
[mm]
- długośc piasty koła czwartego
L +
+ +
+ −
−
p
e7 h h1 s e1 7.5
l :=
1
1000
l =
1
0.083
[m]
7.5 + e +
1
+ ⋅
1
e
Lp
2
2
l :=
=
2
l
[m]
1000
2
0.046
7.5 + e + +
+
+
⋅
1
e
b34 e2 Lp2 2
l :=
=
3
l
[m]
1000
3
0.083
1
11.5 + e + +
⋅
1
e
Lp2 2
l :=
=
4
l
[m]
1000
4
0.05
1
Lp ⋅
+
1
+ ⋅
2
e
b
2
2
2
34
l :=
=
5
l
[m]
1000
5
0.045
1 ⋅b + e + e + 11.5
2
34
1
l :=
=
6
l
[m]
1000
6
0.042
11.5 + e + +
+
1
+ ⋅
1
e
Lp2 e2
b
2
34
l :=
=
7
l
[m]
1000
7
0.095
1 ⋅b + e + e + 11.5
2
34
1
l :=
=
8
l
[m]
1000
8
0.042
e +
+
+
+ −
−
7
h
h1 Lp4 s e1 11.5
l :=
=
9
l
[m]
1000
9
0.107
Obliczam siły promieniowe na poszczególnych kołach: 3
F
:=
⋅
=
×
r1
Ft1 tan(20deg)
Fr1
1.199
10
[N]
3
F
:=
⋅
=
×
r2
Ft2 tan(20deg)
Fr2
1.177
10
[N]
3
F
:=
⋅
=
×
r3
Ft3 tan(20deg)
Fr3
2.697
10
[N]
3
F
:=
⋅
=
×
r4
Ft4 tan(20deg)
Fr4
2.723
10
[N]
Obliczenia wytrzymałościowe walów:
Wal 1:
Wyznaczam reakcję w płaszczyźnie YOZ:
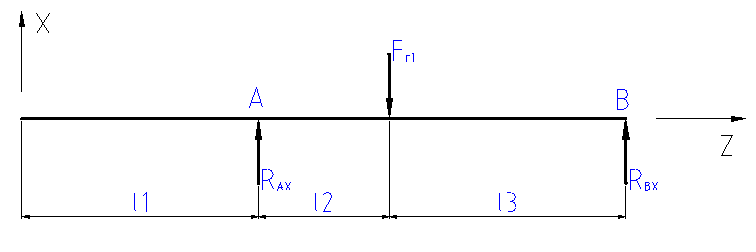
M
:=
iA
∑
0
iA
∑
R
⋅
BY (
+ ) − ⋅ =
BY l2
l3
Ft1 l2
0
F ⋅
t1 l2
3
R
:=
=
×
BY
R
[N]
l +
BY
1.171
10
2
l3
P
:=
iY
∑
0
iY
∑
R
+
−
=
AY
R
AY
BY
Ft1
0
3
R
:=
−
=
×
AY
Ft1 RBY
RAY
2.123
10
[N]
Wyznaczam reakcję w płaszczyźnie XOZ:
M
:=
iA
∑
0
iA
∑
−F ⋅ + R
⋅
BX (
+ ) =
r1 l2
RBX l2 l3
0
r1 l2
R
:=
=
BX
R
[N]
l +
BX
426.062
2
l3
P
:=
iX
∑
0
iX
∑
R
−
+ R
:=
AX
F
AX
r1
R
r1
BX
0
BX
R
:=
−
=
AX
Fr1 RBX
RAX
772.53
[N]
Całkowite reakcje w podporach wałka 1:
2
2
3
R
:=
+
=
×
A
RAX
RAY
RA 2.259 10
[N]
2
2
3
R
:=
+
=
×
B
RBX
RBY
RB
1.246
10
[N]
Momenty gnące w płaszczyźnie XOZ:
Mg
:=
11x
0
[Nm]
Mg
:=
12x
0
[Nm]
Mg
:=
⋅
=
13x
RAX l2
Mg13x
35.15
[Nm]
Mg
:=
14x
0
[Nm]
Moment gnący w płaszczyźnie XOZ
40
30
Mgx 20
10
0
0
83
129
212
l [mm]
Momenty gnące w płaszczyźnie YOZ:
Mg
:=
11y
0
[Nm]
Mg
:=
12y
0
[Nm]
Mg
:=
⋅
=
13y
RAY l2 Mg13y 96.574
[Nm]
:=
14y
0
[Nm]
Moment gnący w płaszczyźnie YOZ
150
100
Mgy
50
0
0
83
129
212
l [mm]
Wypadkowe momenty gnące :
2
2
Mg
:=
+
=
11
Mg11x
Mg11y
Mg11
0
[Nm]
2
2
Mg
:=
+
=
12
Mg12x
Mg12y
Mg12
0
[Nm]
2
2
Mg
:=
+
=
13
Mg13x
Mg13y
Mg13
102.772
[Nm]
2
2
Mg
:=
+
=
14
Mg14x
Mg14y
Mg14
0
[Nm]
Moment gnący wypadkowy
150
100
Mgw
50
0
0
83
129
212
l [mm]
Z
:=
go
508
[MPa]
Z
:=
so
302
[MPa]
Z
α
go
:=
α = 0.841
2⋅Zso
Wyznaczam momenty zastępcze:
Wyznaczam momenty zastępcze: 2
M
:=
(α⋅ )2
+
=
z11
Mg11
M1
Mz11
41.545
[Nm]
2
M
:=
(α⋅ )2
+
=
z12
Mg12
M1
Mz12
41.545
[Nm]
2
M
:=
(α⋅ )2
+
=
z13
Mg13
M1
Mz13
110.852
[Nm]
2
M
:=
(α⋅ )2
+
=
z14
Mg14
M1
Mz14
41.545
[Nm]
Moment gnący zastępczy
150
100
Mgz
50
0
0
83
129
212
l [mm]
Wyznaczam średnice teoretyczne wału 1:
3 32⋅M ⋅
z11 1000
d
:=
=
11
d
[mm]
π⋅
11
11.05
kgo
3 32⋅M ⋅
z12 1000
d
:=
=
12
d
[mm]
π⋅
12
11.05
kgo
3 32⋅M ⋅
z13 1000
d
:=
=
13
d
[mm]
π⋅
13
15.326
kgo
3 32⋅M ⋅
z14 1000
d
:=
=
14
d
[mm]
π⋅
14
11.05
kgo
Średnica teoretyczna wałka
15
d [mm] 10
5
0
0
50
100
150
200
l [mm]
Wał 2:
Wyznaczam reakcję w płaszczyźnieYOZ:
M
:=
iC
∑
0
iC
∑
R
⋅
DY (
+ + ) − ⋅ − ⋅( + ) =
DY l4
l5 l6
Ft2 l4 Ft3 l4 l5
0
F ⋅
+
⋅( + )
t2 l4
Ft3 l4 l5
3
R
:=
=
×
DY
R
[N]
l +
+
DY
6.325
10
4
l5 l6
P
:=
iY
∑
0
iY
∑
R
+
−
−
=
CY
R
CY
DY
Ft2 Ft3
0
3
R
:=
+
−
=
×
CY
Ft2 Ft3 RDY
RCY
4.317
10
[N]
Wyznaczam reakcję w płaszczyźnie XOZ:
M
:=
iC
∑
0
iC
∑
−F ⋅ −
⋅( + ) + R ⋅
DX (
+ + ) =
r2 l4
Fr3 l4 l5
RDX l4 l5 l6
0
F ⋅
+
⋅( + )
r2 l4
Fr3 l4 l5
3
R
:=
=
×
DX
R
[N]
l +
+
DX
2.302
10
4
l5 l6
P
:=
iX
∑
0
iX
∑
R
−
− F + R
:=
CX
F
CX
r2
F
r2
r3
R
r3
DX
0
DX
3
R
:=
+
−
=
×
CX
Fr2 Fr3 RDX
RCX
1.571
10
[N]
Calkowite reakcje w podporach wałka 2:
2
2
3
R
:=
+
=
×
C
RCX
RCY
RC
4.594
10
[N]
2
2
3
R
:=
+
=
×
D
RDX
RDY
RD
6.731
10
[N]
Momenty gnące w płaszczyźnie XOZ:
Mg
:=
21x
0
[Nm]
Mg
:= −
⋅
= −
22x
RCX l4 Mg22x
77.785
[Nm]
Mg
:= −
⋅( + ) + ⋅
= −
23x
RCX l4 l5
Fr2 l5
Mg23x
95.542
[Nm]
Mg
:=
24x
0
[Nm]
Moment gnący w płaszczyźnie XOZ
0
0
50
95
137
Moment gnący w płaszczyźnie XOZ
0
0
50
95
137
-50
Mgx
-100
-150
l [mm]
Momenty gnące w płaszczyźnie YOZ:
[Nm]
Mg
:=
21y
0
Mg
:= −
⋅
= −
22y
RCY l4
Mg22y
213.712
[Nm]
Mg
:= −
⋅( + ) + ⋅
= −
23y
RCY l4 l5
Ft2 l5 Mg23y
262.5
[Nm]
Mg
:=
24y
0
[Nm]
Moment gnący w płaszczyźnie YOZ
0
0
50
95
137
-100
Mgy
-200
-300
l [mm]
Wypadkowy moment gnący:
2
2
Mg
:=
+
=
21
Mg21x
Mg21y
Mg21
0
[Nm]
2
2
Mg
:=
+
=
22
Mg22x
Mg22y
Mg22
227.427
[Nm]
2
2
Mg
:=
+
=
23
Mg23x
Mg23y
Mg23
279.347
[Nm]
2
Mg
:=
+
=
24
Mg24x
Mg24y
Mg24
0
[Nm]
Moment gnący wypadkowy
300
200
Mgw 100
0
0
50
95
137
l [mm]
Wyznaczam momenty zastępcze:
2
M
:=
(α⋅ )2
+
=
z21
Mg21
M2
Mz21
130.868
[Nm]
2
M
:=
(α⋅ )2
+
=
z22
Mg22
M2
Mz22
262.392
[Nm]
2
M
:=
(α⋅ )2
+
=
z23
Mg23
M2
Mz23
308.482
[Nm]
2
M
:=
(α⋅ )2
+
=
z24
Mg24
M2
Mz24
130.868
[Nm]
Moment gnący zastępczy
400
300
Mgz 200
100
0
0
50
95
137
l [mm]
Wyznaczam średnice teoretyczne wału 2:
z21 1000
d
:=
=
21
d
[mm]
π⋅
21
16.198
kgo
3 32⋅M ⋅
z22 1000
d
:=
=
22
d
[mm]
π⋅
22
20.426
kgo
3 32⋅M ⋅
z23 1000
d
:=
=
23
d
[mm]
π⋅
23
21.558
kgo
3 32⋅M ⋅
z24 1000
d
:=
=
24
d
[mm]
π⋅
24
16.198
kgo
Średnica teoretyczna wałka
25
20
15
d [mm] 10
5
0
0
50
100
150
200
l [mm]
Wal 3:
Wyznaczam reakcję w płaszczyźnie XOZ:
M
:=
iE
∑
0
iE
∑
(
)
⋅
FX (
+ ) − ⋅ =
FX l7
l8
Fr4 l7
0
F ⋅
r4 l7
3
R
:=
=
×
FX
R
[N]
l +
FX
1.892
10
7
l8
P
:=
iX
∑
0
iX
∑
R
+
−
=
EX
R
EX
FX
Fr4
0
R
:=
−
=
EX
Fr4 RFX
REX
830.843
[N]
Wyznaczam reakcję w płaszczyźnie YOZ:
M
:=
iE
∑
0
iE
∑
−F ⋅ + R ⋅
FY (
+ ) =
t4 l7
RFY l7 l8
0
F ⋅
t4 l7
3
R
:=
=
×
FY
R
[N]
l +
FY
5.198
10
7
l8
P
:=
iY
∑
0
iY
∑
R
−
+ R
:=
EY
F
EY
t4
R
t4
FY
0
FY
3
R
:=
−
=
×
EY
Ft4 RFY
REY
2.283
10
[N]
Calkowite reakcje w podporach wałka 3:
2
2
3
R
:=
+
=
×
E
REX
REY
RE
2.429
10
[N]
2
2
3
R :=
+
=
×
F
RFX
RFY
RF
5.532
10
[N]
Momenty gnące w płaszczyźnie XOZ: Mg
:=
⋅( + ) − ⋅
=
31x
RFX l8 l7
Fr4 l7 Mg31x
0
[Nm]
Mg
:=
⋅
=
32x
REX l7
Mg32x
78.515
[Nm]
Mg
:=
33x
0
[Nm]
Mg
:=
34x
0
[Nm]
Moment gnący w płaszczyźnie XOZ
100
80
60
Mgx
40
20
0
0
95
137
244
l [mm]
Momenty gnące w płaszczyźnie YOZ:
Mg
:=
⋅( + ) − ⋅
=
31y
RFY l8 l7
Ft4 l7 Mg31y 0
[Nm]
Mg
:=
⋅
=
32y
RFY l8
Mg32y 215.717
[Nm]
Mg
:=
33y
0
[Nm]
Mg
:=
34y
0
[Nm]
Moment gnący w płaszczyźnie YOZ
250
200
150
Mgy 100
50
0
0
95
137
244
l [mm]
2
2
Mg
:=
+
=
31
Mg31x
Mg31y
Mg31
0
[Nm]
2
2
Mg
:=
+
=
32
Mg32x
Mg32y
Mg32
229.561
[Nm]
2
2
Mg
:=
+
=
33
Mg33x
Mg33y
Mg33
0
[Nm]
2
2
Mg
:=
+
=
34
Mg34x
Mg34y
Mg34
0
[Nm]
Moment gnący wypadkowy
250
200
150
Mgw 100
50
0
0
95
137
244
l [mm]
Wyznaczam momenty zastępcze:
2
M
:=
(α⋅ )2
+
=
z31
Mg31
M3
Mz31
654.341
[Nm]
2
M
:=
(α⋅ )2
+
=
z32
Mg32
M3
Mz32
693.441
[Nm]
2
M
:=
(α⋅ )2
+
=
z33
Mg33
M3
Mz33
654.341
[Nm]
2
M
:=
(α⋅ )2
+
=
z34
Mg34
M3
Mz34
654.341
[Nm]
Moment gnący zastępczy
700
680
Mgz 660
640
680
Mgz 660
640
620
0
95
137
244
l [mm]
Wyznaczam średnice teoretyczne wału 3:
3 32⋅M ⋅
z31 1000
d
:=
=
31
d
[mm]
π⋅
31
27.699
kgo
3 32⋅M ⋅
z32 1000
d
:=
=
32
d
[mm]
π⋅
32
28.24
kgo
3 32⋅M ⋅
z33 1000
d
:=
=
33
d
[mm]
π⋅
33
27.699
kgo
3 32⋅M ⋅
z34 1000
d
:=
=
34
d
[mm]
π⋅
34
27.699
kgo
Średnica teoretyczna wałka
28,4
28,2
d [mm]
28
27,8
27,6
0
50
100
150
200
l [mm]
Dla wałka 1 dobieram łożyska walcowe NU2004E
d = 20
[mm]
R
:=
1 = 0.3
[mm]
Lh
10000 [h]
R
=
[mm]
2 = 0.6
[mm]
B = 14
[mm]
D
42
C = 24800 [N]
3 60⋅n ⋅
1 Lh
4
C
:=
⋅
=
×
ob1
RA
C
[N]
6
ob1
2.156
10
10
C > C
Łożysko dobrane prwidłowo.
obl
Dla wałka 2 dobieram łożysko walcowe NU2306E
d = 30
[mm]
R1 = 1.1 [mm]
B = 23 [mm]
D = 72 [mm]
R2 = 1.1 [mm]
C = 67500 [N]
3 60⋅n ⋅
1 Lh
4
C
:=
⋅
=
×
ob2
RD
C
[N]
6
ob2
6.426
10
10
C > C
Łożysko dobrane prawidłowo
ob2
Dla wałka 3 dobieram łożysko wlacowe NU308
d = 40
[mm]
R1 = 1.5
[mm]
B = 23 [mm]
D = 90 [mm]
R2 = 1.5
[mm]
C = 57000 [N]
3 60⋅n ⋅
1 Lh
C
:=
⋅
ob3
RF
4
6
C
=
×
10
ob3
5.281
10
C > C
Łożysko dobrane prawidłowo
ob3
