PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

1. DANE WST

Ę

PNE:

wymiary budynku w osiach konstrukcyjnych:

•

- szeroko

ść

budynku:

B

30.5m

:=

- długo

ść

budynku:

L

60m

:=

- wysoko

ść

od poziomu "0" do osi pasa dolnego:

H0

8.5m

:=

rozstaw wi

ą

zarów kratowych na długo

ś

ci hali:

•

aw

6m

:=

wysoko

ść

wi

ą

zara w kalenicy:

•

hwk

3.0m

:=

wysoko

ść

wi

ą

zara w okapie:

•

hwo

1.5m

:=

wysoko

ść

budynku przy okapie:

•

Hbo

H0 hwo

+

:=

Hbo 10m

=

wysoko

ść

budynku w kalenicy (całkowita):

•

Hbk

H0 hwk

+

:=

Hbk 11.5 m

=

k

ą

t pochylenia połaci dachowej:

•

α

p

atan

hwk hwo

−

0.5 B

⋅













:=

α

p

5.62 deg

⋅

=

rozstaw płatwi wzdłu

ż

wi

ą

zara (w rzucie):

•

apr

2.55m

:=

rozstaw płatwi wzdłu

ż

wi

ą

zara w płaszczy

ź

nie dachu:

•

ap

apr

cos

α

p

( )

:=

ap 2.56 m

=

rodzaj pokrycia dachu:

•

nieocieplony -blacha trapezowa T55

lokalizacja budynku:

•

Zamo

ść

1.1 DANE MATERIAŁOWE:

gatunek stali konstrukcyjnej:

•

S355

parametry wytrzymało

ś

ciowe:

•

fy

355MPa

:=

fyb

fy

:=

fu

510MPa

:=

E

210GPa

:=

G

81GPa

:=

α

12 10

6

−

⋅

1

K

:=

ν

0.3

:=

współczynniki cz

ęś

ciowe:

•

γ

M0

1.0

:=

γ

M1

1.0

:=

γ

M2

1.25

:=

2. ZESTAWIENIE OBCI

Ąś

E

Ń

NA POŁA

Ć

DACHOW

Ą

:

współczynniki bezpiecze

ń

stwa dla obci

ąż

e

ń

stałych:

•

- dla efektów niekorzystnych:

γ

G.sup

1.35

:=

- dla efektów korzystnych:

γ

G.inf

1.00

:=

współczynniki bezpiecze

ń

stwa dla obci

ąż

e

ń

zmiennych:

•

- dla efektów niekorzystnych:

γ

Q

1.50

:=

współczynniki bezpiecze

ń

stwa dla obci

ąż

enia wiatrem i

ś

niegiem:

•

- dla efektów niekorzystnych:

γ

ws

1.50

:=

UWAGA: Obci

ąż

enia obliczeniowe zostały automatycznie wygenerowane przez program obliczeniowy

UWAGA: Obci

ąż

enia od ci

ęż

aru własnego konstrukcji zostały uwzgl

ę

dnione automatycznie

Projektował: Artur Sta

ń

czewski

Strona 1

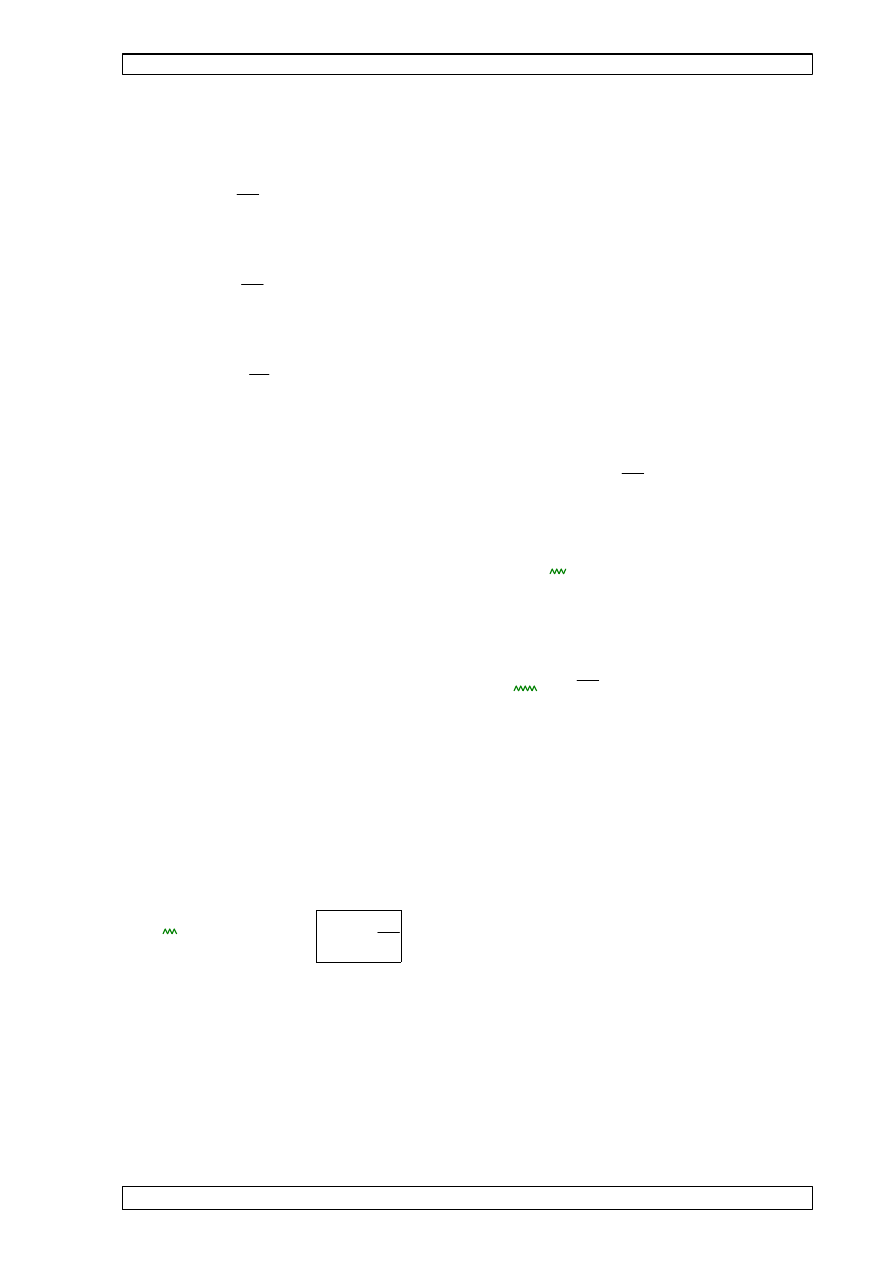
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

2.1 ZESTAWIENIE OBCI

Ąś

E

Ń

STAŁYCH:

blacha trapezowa T-55 o grubo

ś

ci 1mm:

•

g1k

0.1

kN

m

2

⋅

:=

obci

ąż

enie zast

ę

pcze od st

ęż

e

ń

i podwieszonych instalacji:

•

g2k

0.10

kN

m

2

:=

ci

ęż

ar płatwi dachowej - C300x60x3:

•

g3k

0.106

kN

m

:=

2.2 ZESTAWIENIE OBCI

Ąś

E

Ń

EKSPLOATACYJNYCH:

obci

ąż

enie eksploatacyjne dachu dla kategorii H:

•

qk

0.4

kN

m

2

:=

2.3 ZESTAWIENIE OBCI

Ąś

ENIA

Ś

NIEGIEM:

warto

ść

obci

ąż

enia

ś

niegiem gruntu (strefa 3 - Zamo

ść

):

•

A

215

:=

m n.p.m

sk

0.006 A

⋅

0.6

−

:=

sk 0.69

=

i

sk>=1,2 kN/m

2

Przyj

ę

to:

sk

1.2

kN

m

2

:=

współczynnik kształtu dachu (dach dwupołaciowy):

•

dla

0

α

p

≤

30deg

≤

1

=

μ

1

0.8

:=

współczynnik ekspozycji (teren normalny):

•

Ce

1.0

:=

współczynnik termiczny (dach ocieplony):

•

Ct

1

:=

warto

ść

charakterystyczna obci

ąż

enia

ś

niegiem dachu:

•

s

μ

1 Ce

⋅

Ct

⋅

sk

⋅

:=

s

0.96

kN

m

2

⋅

=

2.4 ZESTAWIENIE OBCI

Ąś

ENIA WIATREM:

wyznaczenie bazowej pr

ę

dko

ś

ci wiatru:

•

- warto

ść

podstawowa bazowej pr

ę

dko

ś

ci wiatru (strefa 1 - Zamo

ść

):

vb.0

22

:=

teren kategorii II:

z0

0.05m

:=

zmin

2m

:=

zmax

200m

:=

wysoko

ść

nad poziomem gruntu:

z

H0 hwk

+

:=

z

11.5 m

=

Projektował: Artur Sta

ń

czewski

Strona 2

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

- współczynnik kierunkowy:

cdir

1.0

:=

- współczynnik sezonowy:

cseason

1.0

:=

- bazowa pr

ę

dko

ść

wiatru:

vb

cdir cseason

⋅

vb.0

⋅

:=

vb 22

=

wyznaczenie bazowego ci

ś

nienia pr

ę

dko

ś

ci wiatru:

•

ρ

1.25

:=

- g

ę

sto

ść

powietrza:

- bazowe ci

ś

nienie pr

ę

dko

ś

ci wiatru:

qb

1

2

ρ

⋅

vb

2

⋅

:=

qb 302.5

=

wyznaczenie szczytowego ci

ś

nienia pr

ę

dko

ś

ci wiatru:

•

- wyznaczenie

ś

redniej pr

ę

dko

ś

ci wiatru v

m

:

współczynnik orografii:

co z

( )

1

:=

współczynnik chropowato

ś

ci terenu:

cr z

( )

z0.II

0.05m

:=

(teren kategorii II)

kr

0.19

z0

z0.II









0.07

⋅

:=

kr 0.19

=

cr z

( )

kr ln

z

z0













⋅

:=

cr z

( )

1.03

=

vm z

( )

cr z

( ) co z

( )

⋅

vb

⋅

:=

vm z

( )

22.73

=

- wyznaczenie turbulencji wiatru: Iv z

( )

współczynnik turbulencji:

kI

1.0

:=

odchylenie standardowe:

σ

v

kr vb

⋅

kI

⋅

:=

σ

v

4.18

=

Iv z

( )

kI

co z

( ) ln

z

z0













⋅

:=

Iv z

( )

0.18

=

qp1 z

( )

1

7 Iv z

( )

⋅

+

(

)

0.5

⋅

ρ

⋅

vm z

( )

2

⋅

:=

qp1 z

( )

738.64

=

qp z

( )

qp1 z

( ) Pa

⋅

:=

qp z

( )

0.74 kPa

⋅

=

wyznaczenie obci

ąż

enia wiatrem połaci dachu:

•

bh

L

:=

hh

H0 hwk

+

:=

ed

min bh 2 hh

⋅

,

(

)

:=

ed

2

11.5 m

=

ed

4

5.75 m

=

ed

10

2.3 m

=

α

p

5.62 deg

⋅

=

k

ą

t nachylenia połaci

Projektował: Artur Sta

ń

czewski

Strona 3

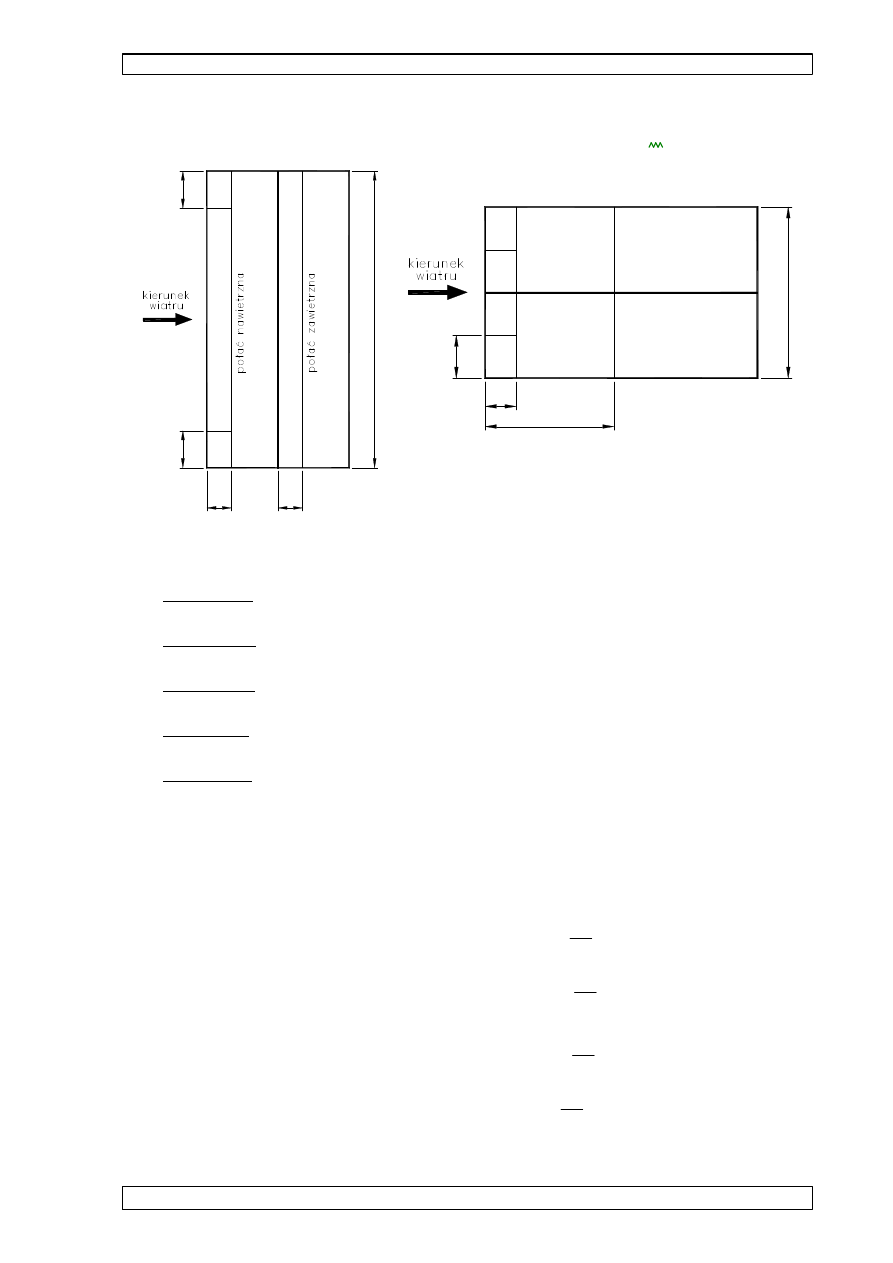
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

SCHEMAT 1

θ

0deg

:=

SCHEMAT 2

θ

90deg

:=

b

F

F

G

H

J

I

e

/4

e/10

e

/4

e/10

F

G

F

G

H

H

I

I

b

e/10

e/2

e

/4

współczynniki ci

ś

nienia zewn

ę

trznego dla dachu dwuspadowego:

•

- dla cz

ęś

ci F:

cpe.F

1.65

−

:=

- dla cz

ęś

ci G:

cpe.G

1.17

−

:=

- dla cz

ęś

ci H:

cpe.H

0.58

−

:=

- dla cz

ęś

ci I:

cpe.I

0.58

−

:=

- dla cz

ęś

ci J:

cpe.J

0.62

−

:=

współczynniki ci

ś

nienia wewn

ę

trznego dla dachu dwuspadowego:

•

cpi1

0.3

−

:=

cpi2

0.2

:=

przyjmujemy

cpi

cpi2

:=

wyznaczenie ci

ś

nienia wiatru na powierzchni

ę

dachu:

•

- dla cz

ęś

ci F:

wF

qp z

( ) cpe.F cpi

−

(

)

⋅

1.37

−

kN

m

2

⋅

=

:=

- dla cz

ęś

ci G:

wG

qp z

( ) cpe.G cpi

−

(

)

⋅

1.01

−

kN

m

2

⋅

=

:=

- dla cz

ęś

ci H:

wH

qp z

( ) cpe.H cpi

−

(

)

⋅

0.58

−

kN

m

2

⋅

=

:=

- dla cz

ęś

ci I:

wI

qp z

( ) cpe.I cpi

−

(

)

⋅

0.58

−

kN

m

2

⋅

=

:=

Projektował: Artur Sta

ń

czewski

Strona 4

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

- dla cz

ęś

ci J:

wJ

qp z

( ) cpe.J cpi

−

(

)

⋅

0.61

−

kN

m

2

⋅

=

:=

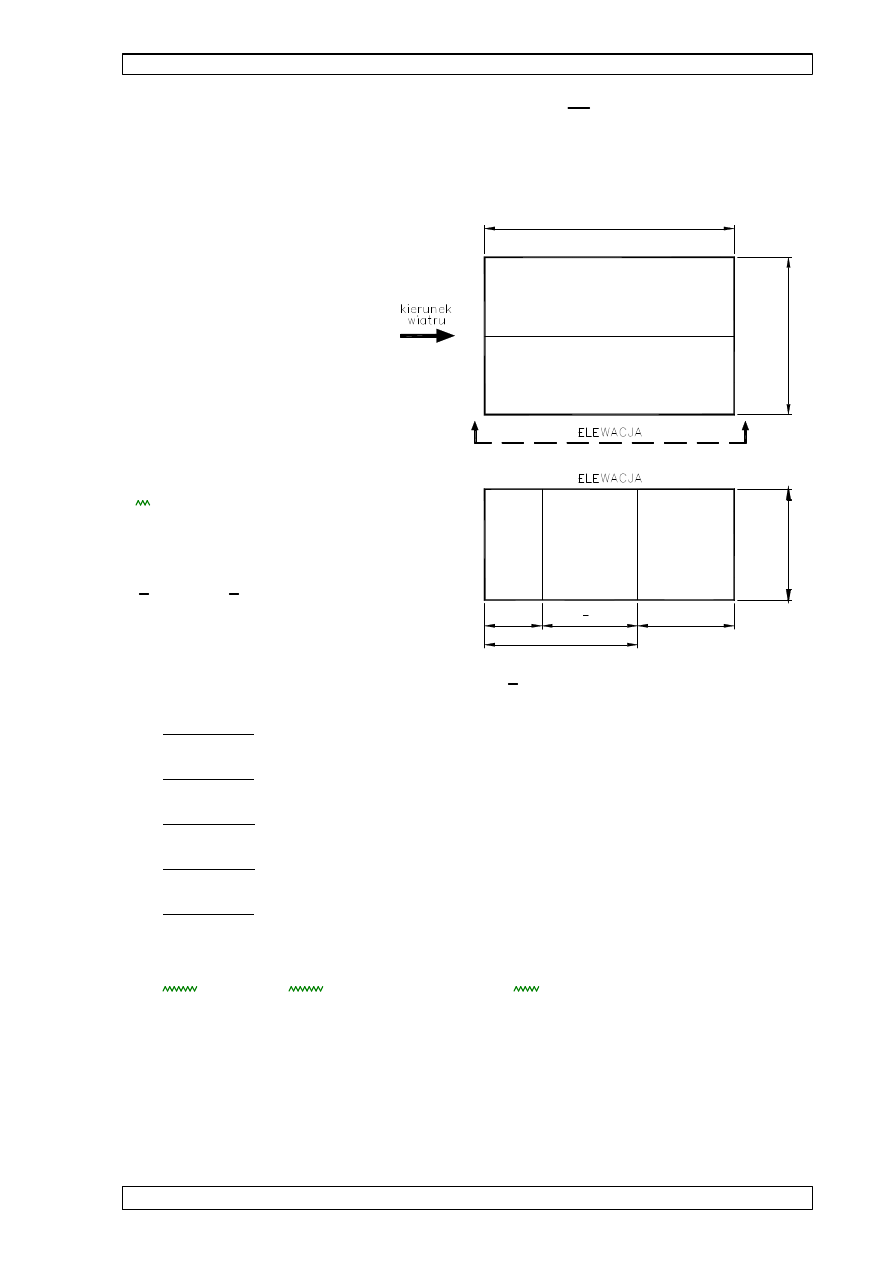
wyznaczenie obci

ąż

enia wiatrem

ś

ciany szczytowej:

•

b

D

E

d

A

B

C

e/5

4
5

e

e

d-e

h

- wymiar poprzeczny do kierunku wiatru:

b

B

30.5 m

=

:=

- wymiar równoległy do kierunku wiatru:

d

L

60 m

=

:=

- wysoko

ść

budynku:

h

Hbk 11.5 m

=

:=

h

b

<

1

=

- budynek traktujemy jak jedn

ą

cz

ęść

na całej wysoko

ś

ci

ś

ciany szczytowej

e

min b 2 h

⋅

,

(

)

:=

e

23 m

=

e

d

<

1

=

- elewacj

ę

dzielimy na pola A, B, C

wg rysunku

e

5

4.6 m

=

4

5

e

⋅

18.4 m

=

d

e

−

37 m

=

współczynniki ci

ś

nienia zewn

ę

trznego dla

ś

cian:

•

h

d

0.19

=

- dla cz

ęś

ci A:

cpe.A

1.20

−

:=

- dla cz

ęś

ci B:

cpe.B

0.80

−

:=

- dla cz

ęś

ci C:

cpe.C

0.50

−

:=

- dla cz

ęś

ci D:

cpe.D

0.70

:=

- dla cz

ęś

ci E:

cpe.E

0.30

−

:=

współczynniki ci

ś

nienia wewn

ę

trznego dla

ś

cian:

•

cpi1

0.3

−

:=

cpi2

0.2

:=

przyjmujemy

cpi

cpi2

:=

Projektował: Artur Sta

ń

czewski

Strona 5

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

wyznaczenie ci

ś

nienia wiatru na powierzchni

ę

dachu:

•

- dla cz

ęś

ci A:

wA

qp z

( ) cpe.A cpi

−

(

)

⋅

1.03

−

kN

m

2

⋅

=

:=

- dla cz

ęś

ci B:

wB

qp z

( ) cpe.B cpi

−

(

)

⋅

0.74

−

kN

m

2

⋅

=

:=

- dla cz

ęś

ci C:

wC

qp z

( ) cpe.C cpi

−

(

)

⋅

0.52

−

kN

m

2

⋅

=

:=

- dla cz

ęś

ci D:

wD

qp z

( ) cpe.D cpi

+

(

)

⋅

0.66

kN

m

2

⋅

=

:=

- dla cz

ęś

ci E:

wE

qp z

( ) cpe.E cpi

−

(

)

⋅

0.37

−

kN

m

2

⋅

=

:=

5. DOBÓR BLACHY TRAPEZOWEJ.

obci

ąż

enie działajace na blach

ę

:

•

- charakterystyczne:

Qk.poł

g1k g2k

+

qk

+

s cos

α

p

( )

⋅

+

1.56

kN

m

2

⋅

=

:=

- obliczeniowe:

Qd.poł

γ

G.sup g1k

⋅

γ

G.sup g2k

⋅

+

γ

Q qk

⋅

+

γ

ws s

⋅

cos

α

p

( )

⋅

+

...

2.3

kN

m

2

⋅

=

:=

rozpi

ę

to

ść

prz

ę

seł blachy:

•

lbl

ap 2.56 m

=

:=

dopuszczalne obci

ąż

enia blachy T55 o gr.1 mm - belka trójprz

ę

słowa przy rozstawie podpór 2.55

•

m (wg tablic firmy "Blachy Pruszy

ń

ski"):

- obci

ąż

enie blachy z uwagi na no

ś

no

ść

:

Qdop

5.49kPa

:=

- obci

ąż

enie blachy z uwagi na strzałk

ę

ugi

ę

cia L/150:

Q150

5.49kPa

:=

- obci

ąż

enie blachy z uwagi na strzałk

ę

ugi

ę

cia L/200:

Q200

5.39kPa

:=

- obci

ąż

enie blachy z uwagi na strzałk

ę

ugi

ę

cia L/300:

Q300

3.61kPa

:=

warunki no

ś

no

ś

ci:

•

Qd.poł Qdop

≤

1

=

warunek spełniony

Qk.poł Q150

≤

1

=

warunek spełniony

Qk.poł Q200

≤

1

=

warunek spełniony

Qk.poł Q300

≤

1

=

warunek spełniony

Przyj

ę

to blach

ę

trapezow

ą

T55 o grubo

ś

ci 1 mm.

6. DOBÓR PŁATWI DACHOWEJ.

obci

ąż

enie połaci dachu:

•

- charakterystyczne:

Qk.poł

g1k g2k

+

qk

+

s cos

α

p

( )

⋅

+

1555.39 Pa

=

:=

- obliczeniowe:

Qd.poł

γ

G.sup g1k

⋅

γ

G.sup g2k

⋅

+

γ

Q qk

⋅

+

γ

ws s

⋅

cos

α

p

( )

⋅

+

...

2303.08 Pa

=

:=

Projektował: Artur Sta

ń

czewski

Strona 6

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

rozpi

ę

to

ść

płatwi:

•

lp

aw

:=

rozstaw płatwi wzdłu

ż

połaci:

•

ap 2.56 m

=

obci

ąż

enie równomierne płatwi:

•

- charakterystyczne:

Qk.p

Qk.poł ap

⋅

3.99

kN

m

⋅

=

:=

- obliczeniowe:

Qd.p

Qd.poł ap

⋅

5.9

kN

m

⋅

=

:=

dopuszczalne obci

ąż

enia płatwi C/300x60x3 (wg tablic firmy "Blachy Pruszy

ń

ski"):

•

- obci

ąż

enie połaci przy rozp. 6m i rozstawie 2.56m:

Qdop

7.82kPa

:=

- równomierne obci

ąż

enie płatwi (Qd+N):

Qdn

17.96

kN

m

:=

- równomierne obci

ąż

enie płatwi (L/200):

Qk

19.55

kN

m

:=

warunki no

ś

no

ś

ci:

•

Qd.poł Qdop

≤

1

=

warunek spełniony

Qd.poł

Qdop

0.29

=

Qd.poł

Qdop

0.8

≤

1

=

Qd.p Qdn

≤

1

=

warunek spełniony

Qd.p

Qdn

0.33

=

Qd.p

Qdn

0.8

≤

1

=

Qk.p Qk

≤

1

=

warunek spełniony

Qk.p

Qk

0.2

=

Qk.p

Qk

0.8

≤

1

=

Przyj

ę

to płatew zimnogi

ę

t

ą

C/300x60x3.

7. OBLICZENIA PŁATWI DACHOWEJ WG PN-EN-1993-1-3.

7.1 ZESTAWIENIE OBCI

Ąś

E

Ń

NA PŁATEW.

7.1.1 ZESTAWIENIE OBCI

Ąś

E

Ń

STAŁYCH.

G1k

g1k

( )

ap

⋅

g3k

+

:=

G1k 0.36

kN

m

⋅

=

7.1.2 ZESTAWIENIE OBCI

Ąś

E

Ń

EKSPLOATACYJNYCH.

Q1k

qk ap

⋅

:=

Q1k 1.02

kN

m

⋅

=

7.1.3 ZESTAWIENIE OBCI

Ąś

ENIA

Ś

NIEGIEM.

S1k

s ap

⋅

cos

α

p

( )

⋅

:=

S1k 2.45

kN

m

⋅

=

7.1.4 ZESTAWIENIE OBCI

Ąś

ENIA WIATREM - WG SCHEMATU 1.

W1k

wF 0.5

⋅

ap

⋅

wH 0.5

⋅

ap

⋅

+

:=

W1k

2.49

−

kN

m

⋅

=

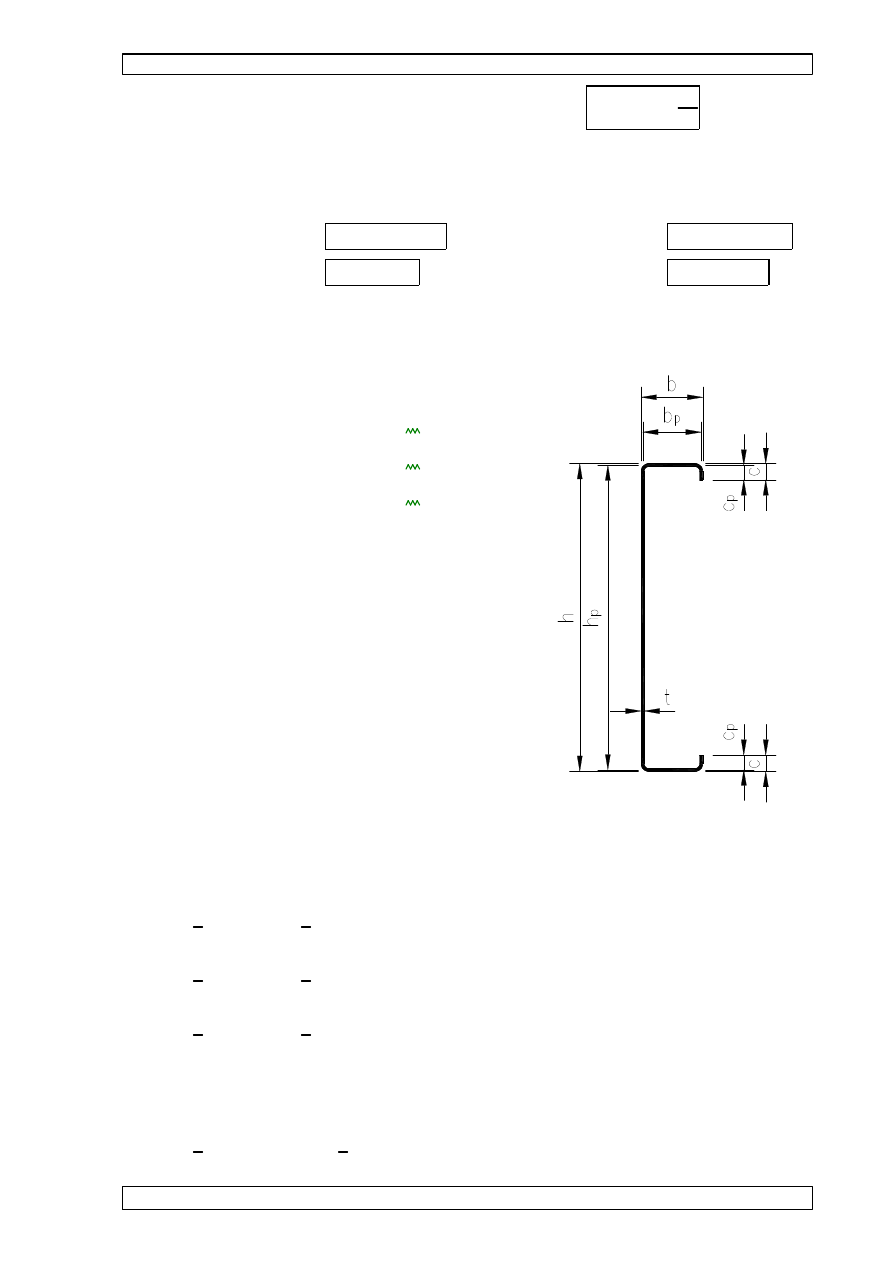
7.2 OBLICZENIE SKŁADOWYCH OBCI

Ąś

E

Ń

.

Projektował: Artur Sta

ń

czewski

Strona 7

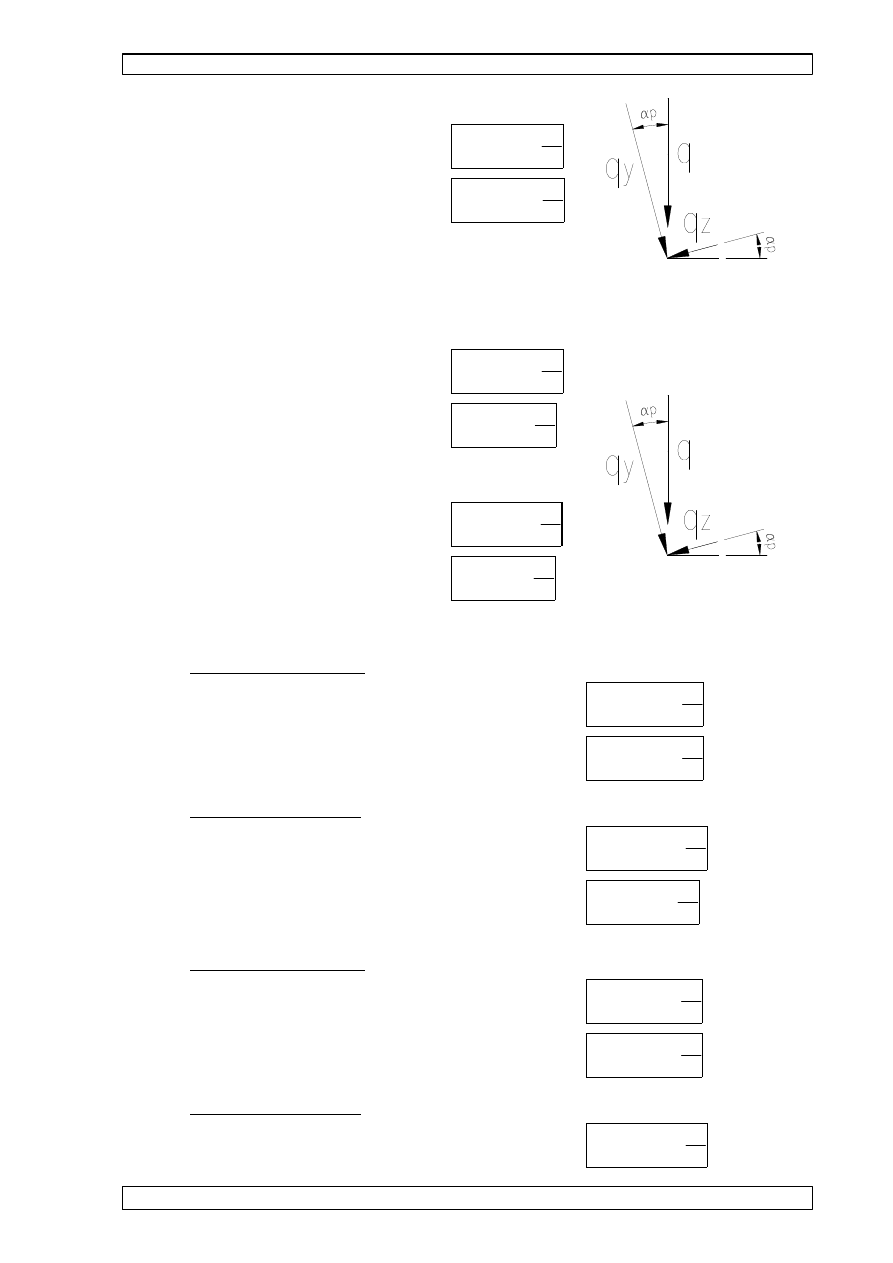
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

obci

ąż

enie stałe:

•

G1k.y

G1k cos

α

p

( )

⋅

:=

G1k.y 0.36

kN

m

⋅

=

G1k.z

G1k sin

α

p

( )

⋅

:=

G1k.z 0.04

kN

m

⋅

=

obci

ąż

enie eksploatacyjne:

•

Q1k.y

Q1k cos

α

p

( )

⋅

:=

Q1k.y 1.02

kN

m

⋅

=

Q1k.z

Q1k sin

α

p

( )

⋅

:=

Q1k.z 0.1

kN

m

⋅

=

obci

ąż

enie

ś

niegiem:

•

S1k.y

S1k cos

α

p

( )

⋅

:=

S1k.y 2.44

kN

m

⋅

=

S1k.z

Q1k sin

α

p

( )

⋅

:=

S1k.z 0.1

kN

m

⋅

=

7.3 KOMBINACJE OBCI

Ąś

E

Ń

.

KOMBINACJA SGN - max:

•

ppds.y

G1k.y

γ

G.sup

⋅

Q1k.y

γ

Q

⋅

+

S1k.y

γ

ws

⋅

+

:=

ppds.y 5.67

kN

m

⋅

=

ppds.z

G1k.z

γ

G.sup

⋅

Q1k.z

γ

Q

⋅

+

S1k.z

γ

ws

⋅

+

:=

ppds.z 0.35

kN

m

⋅

=

KOMBINACJA SGN - min:

•

ppdi.y

G1k.y

γ

G.inf

⋅

W1k

γ

ws

⋅

+

:=

ppdi.y

3.37

−

kN

m

⋅

=

ppdi.z

G1k.z

γ

G.inf

⋅

:=

ppdi.z 0.04

kN

m

⋅

=

KOMBINACJA SGU - max:

•

ppks.y

G1k.y Q1k.y

+

S1k.y

+

:=

ppks.y 3.82

kN

m

⋅

=

ppks.z

G1k.z Q1k.z

+

S1k.z

+

:=

ppks.z 0.24

kN

m

⋅

=

KOMBINACJA SGU - min:

•

ppki.y

G1k.y W1k

+

:=

ppki.y

2.13

−

kN

m

⋅

=

Projektował: Artur Sta

ń

czewski

Strona 8

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

ppki.z

G1k.z

:=

ppki.z 0.04

kN

m

⋅

=

7.4 OBLICZENIE SIŁ WEWN

Ę

TRZNYCH.

kombinacja SGN - max:

kombinacja SGN - min:

My.s

0.125 ppds.y

⋅

lp

2

⋅

:=

My.s 25.52 kNm

⋅

=

My.i

0.125 ppdi.y

⋅

lp

2

⋅

:=

My.i

15.18

−

kNm

⋅

=

Mz.s

0.080 ppds.z

⋅

lp

2

⋅

:=

Mz.s 1 kNm

⋅

=

Mz.i

0.080 ppdi.z

⋅

lp

2

⋅

:=

Mz.i 0.1 kNm

⋅

=

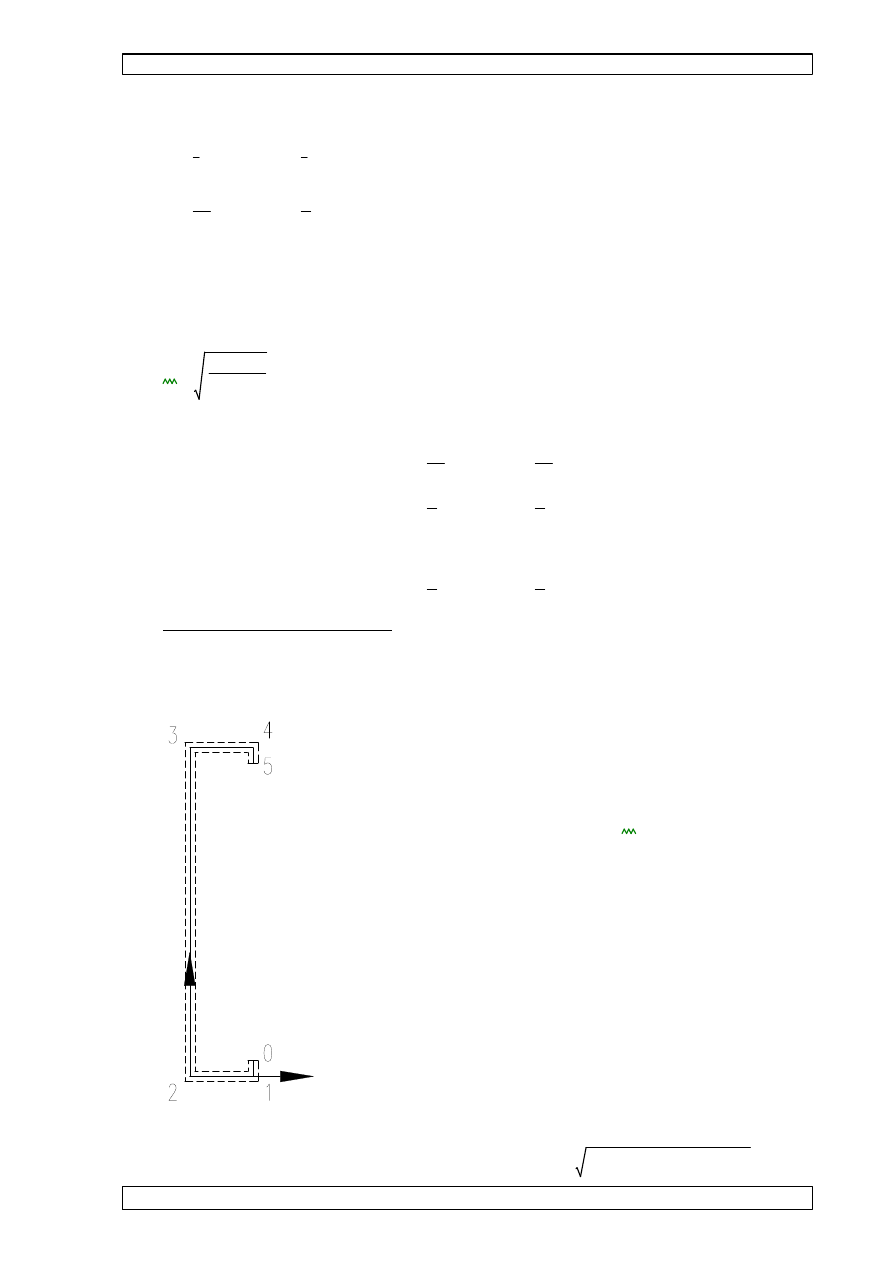
7.5 WYMIARY PRZEKROJU POPRZECZNEGO PŁATWI.

Przyj

ę

to płatew C/300x60x3 (wg tablic firmy "Blachy Pruszy

ń

ski")

wysoko

ść

płatwi:

•

h

300mm

:=

szeroko

ść

półki górnej i dolnej:

•

b

60mm

:=

usztywnienie brzegowe:

•

c

20mm

:=

nominalna grubo

ść

ś

cianek:

•

tnom

3mm

:=

tzinc

0.04mm

:=

grubo

ść

obliczeniowa:

•

t

tnom tzinc

−

:=

t

2.96 mm

⋅

=

promie

ń

zaokr

ą

glenia:

•

r

1.5 t

⋅

4.44 mm

⋅

=

:=

hp

h

tnom

−

:=

bp

b

tnom

−

:=

cp

c

0.5 tnom

⋅

−

:=

7.6 SPRAWDZENIE PROPORCJI GEOMETRYCZNYCH PŁATWI.

maksymalne stosunki szeroko

ś

ci do grubo

ś

ci

ś

cianek (1993-1-3, tab.5.1):

•

b

t

20.27

=

b

t

60

≤

1

=

- warunek spełniony

c

t

6.76

=

c

t

50

≤

1

=

- warunek spełniony

h

t

101.35

=

h

t

500

≤

1

=

- warunek spełniony

proporcje z uwagi na sztywno

ść

i unikni

ę

cie niestateczno

ś

ci usztywnie

ń

•

(1993-1-3, 5.2a):

c

b

0.33

=

0.2

c

b

≤

0.6

≤

1

=

- warunek spełniony

Projektował: Artur Sta

ń

czewski

Strona 9

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

sprawdzenie mo

ż

liwo

ś

ci pomini

ę

cia wpływu naro

ż

y (1993-1-3, 5.1):

•

r

t

1.5

=

r

t

5

≤

1

=

- warunek spełniony

r

bp

0.08

=

r

b

0.1

≤

1

=

- warunek spełniony

Poniewa

ż

spełnione zostały warunki r/t oraz r/b pomijamy wpływ zaokr

ą

glenia naro

ż

y.

7.7 SPRAWDZENIE KLASY PRZEKROJU PŁATWI.

ε

235MPa

fy

:=

ε

0.81

=

sprawdzenie klasy przekroju pasa:

•

- cz

ęść

wewn

ę

trzna

ś

ciskana:

bp

t

19.26

=

bp

t

33

ε

⋅

≤

1

=

33

ε

⋅

26.85

=

klasa 1

- cz

ęść

wspornikowa

ś

ciskana:

c

t

6.76

=

c

t

9

ε

⋅

≤

1

=

9

ε

⋅

7.32

=

klasa 1

sprawdzenie klasy przekroju

ś

rodnika:

•

- cz

ęść

wewn

ę

trzna zginana:

h

t

101.35

=

h

t

124

ε

⋅

≤

0

=

124

ε

⋅

100.89

=

klasa 4

Przekrój płatwi zaliczono do klasy 4

7.8 CECHY GEOMETRYCZNE PRZEKROJU BRUTTO (wyznaczone wg zał

ą

cznika C -

PN-EN-1993-1-3).

z

y

1

2

3

4

5

n

5

:=

j

0 n

..

:=

y

bp

bp

0

0

bp

bp









































:=

z

cp

0

0

hp

hp

hp cp

−









































:=

i

1 n

..

:=

tz

i

t

:=

y

57

57

0

0

57

57





































mm

⋅

=

z

18.5

0

0

297

297

278.5





































mm

⋅

=

pola poszczególnych cz

ęś

ci przekroju:

•

dA

i

tz

i

y

i

y

i 1

−

−

(

)

2

z

i

z

i 1

−

−

(

)

2

+

⋅









→



:=

Projektował: Artur Sta

ń

czewski

Strona 10

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

pole przekroju brutto:

•

A

1

n

i

dA

i

∑

=

:=

A

13.26 cm

2

⋅

=

moment statyczny przekroju wzgl

ę

dem osi y-y oraz współrz

ę

dna

ś

rodka ci

ęż

ko

ś

ci przekroju:

•

Sy0

1

n

i

z

i

z

i 1

−

+

(

)

dA

i

2

⋅













∑

=

:=

zgc

Sy0

A

14.85 cm

⋅

=

:=

moment statyczny przekroju wzgl

ę

dem osi z-z oraz współrz

ę

dna

ś

rodka ci

ęż

ko

ś

ci przekroju:

•

Sz0

1

n

i

y

i

y

i 1

−

+

(

)

dA

i

2

⋅













∑

=

:=

ygc

Sz0

A

1.2 cm

⋅

=

:=

moment bezwładno

ś

ci wzgl

ę

dem osi y-y oraz osi centralnej:

•

Iy0

1

n

i

z

i

( )

2

z

i 1

−

( )

2

+

z

i

z

i 1

−

⋅

+









dA

i

3

⋅













∑

=

:=

Iy0 4527.33 cm

4

⋅

=

Iy

Iy0 A zgc

2

⋅

−

:=

Iy 1603.03 cm

4

⋅

=

moment bezwładno

ś

ci wzgl

ę

dem osi z-z oraz osi centralnej:

•

Iz0

1

n

i

y

i

( )

2

y

i 1

−

( )

2

+

y

i

y

i 1

−

⋅

+









dA

i

3

⋅













∑

=

:=

Iz0 72.13 cm

4

⋅

=

Iz

Iz0 A ygc

2

⋅

−

:=

Iz 53.16 cm

4

⋅

=

od

ś

rodkowy moment bezwładno

ś

ci wzgldem osi pocz

ą

tkowych i centralnych:

•

Iyz0

1

n

i

2 y

i 1

−

⋅

z

i 1

−

⋅

2 y

i

⋅

z

i

⋅

+

y

i 1

−

z

i

⋅

+

y

i

z

i 1

−

⋅

+

(

)

dA

i

6

⋅













∑

=

:=

Iyz0 235.52 cm

4

⋅

=

Iyz

Iyz0

Sy0 Sz0

⋅

A

−

:=

Iyz 0 cm

4

⋅

=

poło

ż

enie głównych osi bezwładno

ś

ci oraz ekstremalne momenty bezwładno

ś

ci:

•

Iz Iy

−

1549.87

−

cm

4

⋅

=

α

1

2

atan

2 Iyz

⋅

Iz Iy

−









:=

α

0

−

deg

⋅

=

I

ξ

1

2

Iy Iz

+

Iz Iy

−

(

)

2

4 Iyz

2

⋅

+

+









⋅

:=

I

ξ

1603.03 cm

4

⋅

=

I

η

1

2

Iy Iz

+

Iz Iy

−

(

)

2

4 Iyz

2

⋅

+

−









⋅

:=

I

η

53.16 cm

4

⋅

=

współrz

ę

dne wycinkowe:

•

Projektował: Artur Sta

ń

czewski

Strona 11

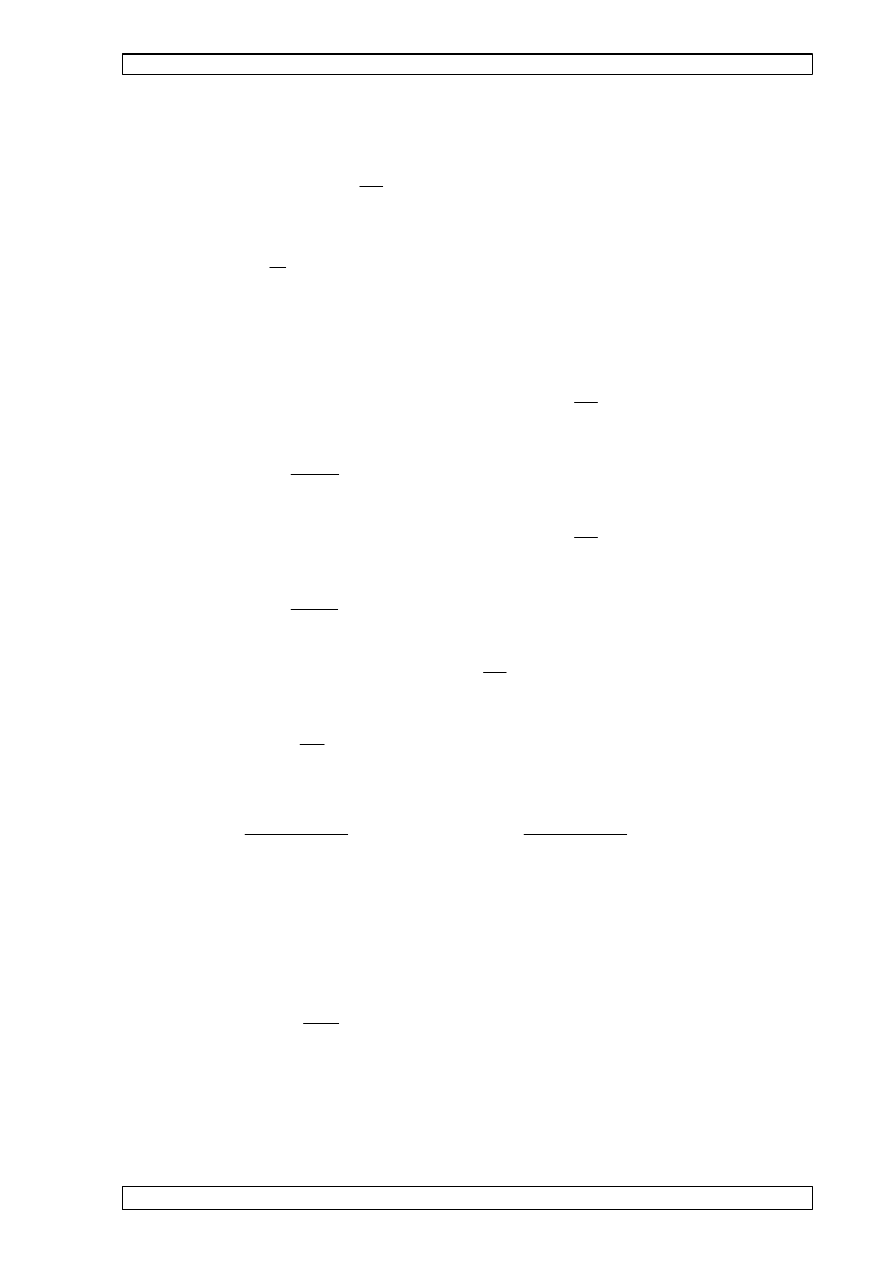
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

ω

0

0

:=

ω

0

i

y

i 1

−

z

i

⋅

y

i

z

i 1

−

⋅

−

:=

ω

i

ω

i 1

−

ω

0

i

+

:=

ś

rednie współrz

ę

dne wycinkowe:

•

I

ω

1

n

i

ω

i 1

−

ω

i

+

(

)

dA

i

2

⋅













∑

=

:=

I

ω

375.35

−

cm

4

⋅

=

ω

mean

I

ω

A

:=

ω

mean

28.31

−

cm

2

⋅

=

stałe wycinkowe:

•

Iy

ω

0

1

n

i

2 y

i 1

−

⋅

ω

i 1

−

⋅

2 y

i

⋅

ω

i

⋅

+

y

i 1

−

ω

i

⋅

+

y

i

ω

i 1

−

⋅

+

(

)

dA

i

6

⋅













∑

=

:=

Iy

ω

0

1238.34

−

cm

5

⋅

=

Iy

ω

Iy

ω

0

Sz0 I

ω

⋅

A

−

:=

Iy

ω

789.42

−

cm

5

⋅

=

Iz

ω

0

1

n

i

2

ω

i 1

−

⋅

z

i 1

−

⋅

2

ω

i

⋅

z

i

⋅

+

ω

i 1

−

z

i

⋅

+

ω

i

z

i 1

−

⋅

+

(

)

dA

i

6

⋅













∑

=

:=

Iz

ω

0

9064.26

−

cm

5

⋅

=

Iz

ω

Iz

ω

0

Sy0 I

ω

⋅

A

−

:=

Iz

ω

3490.29

−

cm

5

⋅

=

I

ωω

0

1

n

i

ω

i

( )

2

ω

i 1

−

( )

2

+

ω

i

ω

i 1

−

⋅

+









dA

i

3

⋅













∑

=

:=

I

ωω

0

3.93 m

2

cm

4

⋅

=

I

ωω

I

ωω

0

I

ω

2

A

−

:=

I

ωω

28646.91 cm

6

⋅

=

współrz

ę

dne

ś

rodka

ś

cinania:

•

ysc

Iz

ω

Iz

⋅

Iy

ω

Iyz

⋅

−

Iy Iz

⋅

Iyz

2

−

:=

zsc

Iy

ω

Iy

⋅

Iz

ω

Iyz

⋅

−

Iy Iz

⋅

Iyz

2

−

:=

wycinkowy moment bezwładno

ś

ci:

•

Iw

I

ωω

zsc Iy

ω

⋅

+

ysc Iz

ω

⋅

−

:=

Iw 32770.4 cm

6

⋅

=

moment bezwładno

ś

ci i wska

ź

nik wytrzymało

ś

ci przy skr

ę

caniu:

•

It

1

n

i

dA

i

tz

i

( )

2

3

⋅









∑

=

:=

It 0.39 cm

4

⋅

=

współrz

ę

dne wycinkowe wzgl

ę

dem

ś

rodka

ś

cinania:

•

ω

s

j

ω

j

ω

mean

−

zsc y

j

ygc

−

(

)

⋅

+

ysc z

j

zgc

−

(

)

⋅

−

:=

maksymalne współrz

ę

dne wycinkowe i wycinkowy wska

ź

nik wytrzymało

ś

ci:

•

Projektował: Artur Sta

ń

czewski

Strona 12

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

ω

max

max

ω

s

( )

:=

ω

max

301.02 cm

2

⋅

=

Ww

Iw

ω

max

:=

Ww 108.87 cm

4

⋅

=

współrz

ę

dne

ś

rodka

ś

cianania wzgl

ę

dem

ś

rodka ci

ęż

ko

ś

ci:

•

ys

ysc ygc

−

:=

ys

33.73

−

mm

⋅

=

zs

zsc zgc

−

:=

zs

297

−

mm

⋅

=

biegunowy moment bezwładno

ś

ci wzgl

ę

dem

ś

rodka

ś

cinania:

•

Ip

Iy Iz

+

A

ys

2

zs

2

+









⋅

+

:=

Ip 13504.3 cm

4

⋅

=

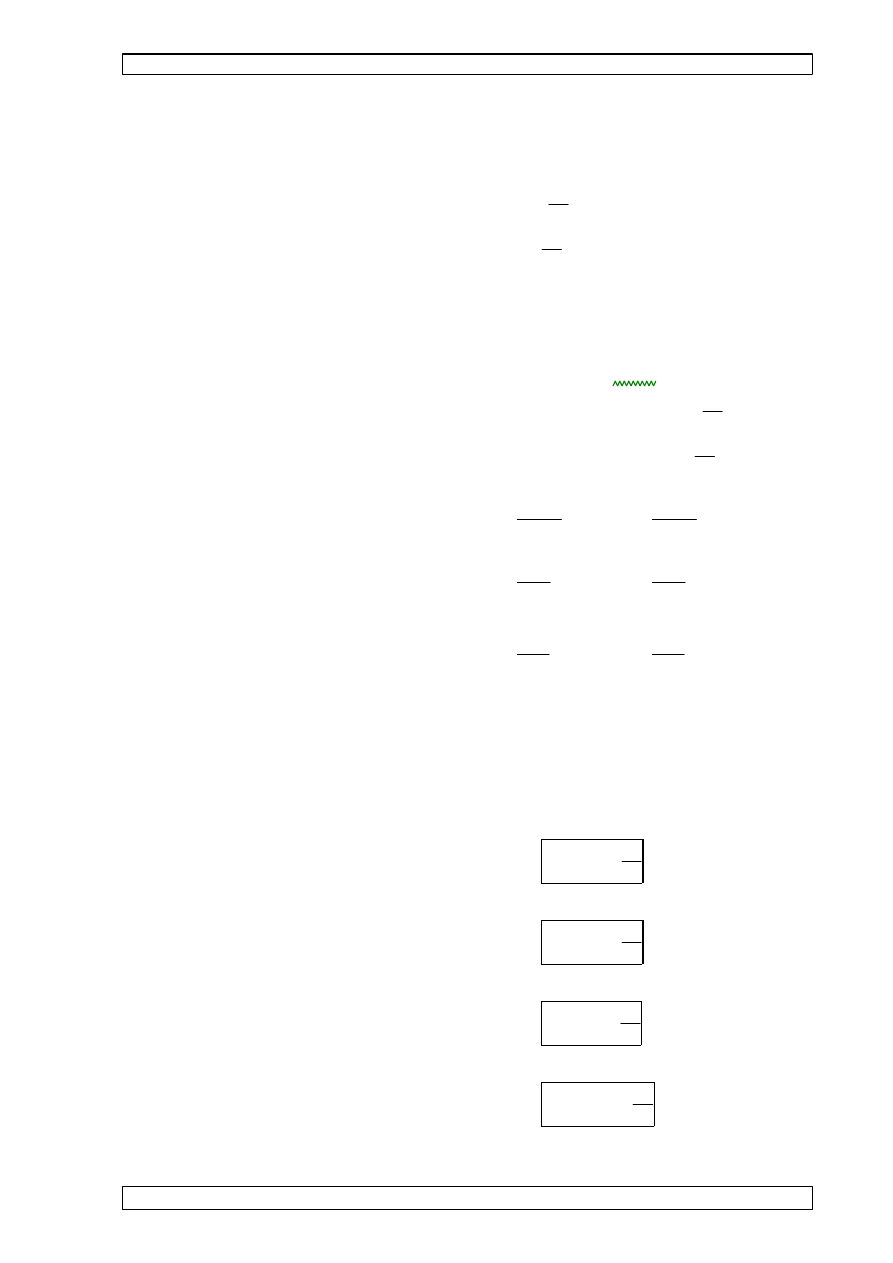
7.9 CECHY GEOMETRYCZNE PRZEKROJU BRUTTO.

z

5

0

y

0

z

y

wymiary przekroju:

•

hp 297 mm

⋅

=

bp 57 mm

⋅

=

cp 18.5 mm

⋅

=

t

2.96 mm

⋅

=

pole przekroju i momenty statyczne płatwi:

•

A

t 2 cp

⋅

2 bp

⋅

+

hp

+

(

)

⋅

:=

A

13.26 cm

2

⋅

=

Sy0

cp t

⋅

0.5

⋅

cp

⋅

hp t

⋅

0.5

⋅

hp

⋅

+

bp t

⋅

hp

⋅

+

cp t

⋅

hp 0.5 cp

⋅

−

(

)

⋅

+

...

196.92 cm

3

⋅

=

:=

Sz0

2 cp t

⋅

bp

⋅

(

)

⋅

2 bp t

⋅

0.5

⋅

bp

⋅

(

)

⋅

+

15.86 cm

3

⋅

=

:=

współrz

ę

dne

ś

rodka ci

ęż

ko

ś

ci:

•

ygc

Sz0

A

1.2 cm

⋅

=

:=

zgc

Sy0

A

14.85 cm

⋅

=

:=

momenty bezwładno

ś

ci wzgl

ę

dem osi centralnych:

•

Iy

2

cp

3

t

⋅

12

cp t

⋅

zgc 0.5 cp

⋅

−

(

)

2

⋅

+













⋅

2

t

3

bp

⋅

12

bp t

⋅

zgc

2

⋅

+













⋅

+

hp

3

t

⋅

12

+

1603.05 cm

4

⋅

=

:=

Iz

2

t

3

cp

⋅

12

cp t

⋅

bp ygc

−

(

)

2

⋅

+













⋅

2

bp

3

t

⋅

12

bp t

⋅

bp 0.5bp

−

ygc

−

(

)

2

⋅

+













⋅

+

t

3

hp

⋅

12

hp t

⋅

ygc

2

⋅

+

+

...

53.23 cm

4

⋅

=

:=

wska

ź

niki wytrzymało

ś

ci:

•

Projektował: Artur Sta

ń

czewski

Strona 13

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

Wy

Iy

zgc

107.95 cm

3

⋅

=

:=

Wz

Iz

bp ygc

−

11.82 cm

3

⋅

=

:=

promienie bezwładno

ś

ci:

•

iy

Iy

A

10.99 cm

⋅

=

:=

iz

Iz

A

2 cm

⋅

=

:=

7.10 OBLICZENIE SZEROKO

Ś

CI CZ

ĘŚ

CI WSPÓŁPRACUJ

Ą

CYCH.

7.10.1 PAS

Ś

CISKANY PŁATWI.

stosunek napr

ęż

e

ń

na brzegach

ś

cianki

ψ

(1993-1-5 4.4 tab.4.1):

•

ψ

σ

2

σ

1

=

ψ

1

:=

parametr niestateczno

ś

ci miejscowej zale

ż

ny od

ψ

(1993-1-5 4.4 tab.4.1):

•

k

σ

4

:=

obliczenie współczynnika redukcyjnego (1993-1-5 4.4):

•

miarodajna szerkoko

ść

ś

cianki:

bp 57 mm

⋅

=

λ

p

bp

t

1

28.4

ε

⋅

k

σ

⋅

⋅

:=

λ

p

0.42

=

λ

p

0.673

<

przyj

ę

to

ρ

1.0

:=

cz

ęść

współpracuj

ą

ca pasa (1993-1-5 4.4 tab.4.1):

•

beff

ρ

bp

⋅

:=

beff 57 mm

⋅

=

be1

0.5 beff

⋅

:=

be1 28.5 mm

⋅

=

be2

0.5 beff

⋅

:=

be2 28.5 mm

⋅

=

7.10.1.1

Ś

CIANKA USZTYWNIENIA BRZEGOWEGO PASA.

stosunek szeroko

ś

ci usztywnienia brzegowego do szeroko

ś

ci pasa (1993-1-3 5.5.3.2):

•

cp

bp

0.32

=

cp

bp

0.35

≤

1

=

przyjmujemy parametr niestateczno

ś

ci

k

σ

0.5

:=

obliczenie współczynnika redukcyjnego (1993-1-5 4.4):

•

miarodajna szerkoko

ść

ś

cianki:

cp 18.5 mm

⋅

=

λ

p

cp

t

1

28.4

ε

⋅

k

σ

⋅

⋅

:=

λ

p

0.38

=

λ

p

0.748

<

przyj

ę

to

ρ

1.0

:=

cz

ęść

współpracuj

ą

ca

ś

cianki (1993-1-3 5.5.3.2):

•

ceff

ρ

cp

⋅

:=

ceff 18.5 mm

⋅

=

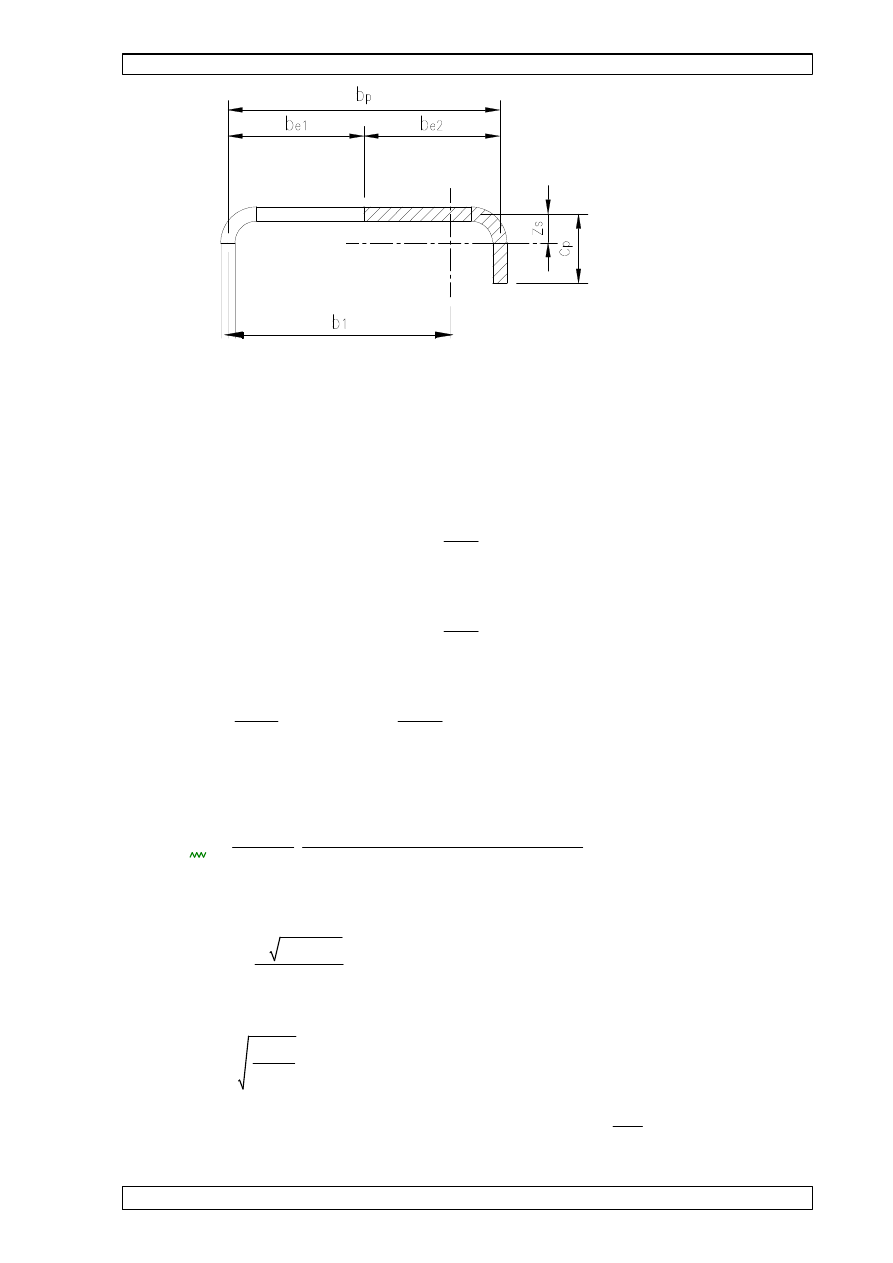
7.10.1.2 CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU USZTYWNIENIA

Projektował: Artur Sta

ń

czewski

Strona 14

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

pole przekroju:

•

As0

t be2 ceff

+

(

)

⋅

:=

As0 1.39 cm

2

⋅

=

moment statyczny:

•

Ssy0

ceff t

⋅

0.5

⋅

ceff

⋅

be2 t

⋅

0.5

⋅

t

⋅

+

:=

Ssy0 0.63 cm

3

⋅

=

Ssz0

ceff t

⋅

0.5

⋅

t

⋅

be2 t

⋅

0.5

⋅

be2

⋅

+

:=

Ssz0 1.28 cm

3

=

poło

ż

enie

ś

rodka ci

ęż

ko

ś

ci:

•

ys0

Ssz0

As0

:=

ys0 9.22 mm

⋅

=

b1.0

beff ys0

−

:=

b1.0 47.78 mm

⋅

=

zs0

Ssy0

As0

:=

zs0 4.54 mm

⋅

=

moment bezwładno

ś

ci:

•

Is0

be2 t

3

⋅

12

be2 t

⋅

zs0

( )

2

⋅

+

ceff

3

t

⋅

12

+

ceff t

⋅

0.5 ceff

⋅

zs0

−

(

)

2

⋅

+

:=

Is0 0.46 cm

4

⋅

=

kf

0

:=

zginanie wzgl

ę

dem osi y-y oraz drugi pas rozci

ą

gany

sztywno

ść

translacyjna pasa:

•

K

0

E t

3

⋅

4 1

ν

2

−

(

)

1

b1.0

( )

2

hp

⋅

b1.0

( )

3

+

0.5 b1.0

⋅

b1.0

⋅

hp

⋅

kf

⋅

+

⋅

:=

napr

ęż

enie krytyczne dla usztywnie

ń

:

•

σ

cr.s0

2

K

0

E

⋅

Is0

⋅

⋅

As0

:=

σ

cr.s0

614.52 MPa

⋅

=

obliczenie współczynnika redukcyjnego z uwagi na wyboczenie dystorsyjne (1993-1-3 5.5.3.1)

•

λ

d0

fyb

σ

cr.s0

:=

λ

d0

0.76

=

χ

d0

if

λ

d0

0.65

≤

1

,

if 0.65

λ

d0

<

1.38

≤

1.47

0.723

λ

d0

⋅

−

,

0.66

λ

d0

,













,













:=

χ

d0

0.92

=

Projektował: Artur Sta

ń

czewski

Strona 15

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

χ

d0

1

<

mo

ż

na iterowa

ć

ITERACJA 1

przyjeto:

∆

5%

:=

Zredukowane wymiary przekroju:

tred1

χ

d0 t

⋅

0.27 cm

⋅

=

:=

b1

1

χ

d0 b1.0

⋅

4.4 cm

⋅

=

:=

be2.1

χ

d0 be2

⋅

2.62 cm

⋅

=

:=

ceff1

χ

d0 ceff

⋅

1.7 cm

⋅

=

:=

fyb1

χ

d0 fyb

⋅

326769.66 kPa

⋅

=

:=

pole przekroju:

•

As1

tred1 be2.1 ceff1

+

(

)

⋅

:=

As1 1.18 cm

2

⋅

=

moment statyczny:

•

Ssy1

ceff1 tred1

⋅

0.5

⋅

ceff1

⋅

be2.1 tred1

⋅

0.5

⋅

tred1

⋅

+

:=

Ssy1 0.49 cm

3

⋅

=

Ssz1

ceff1 tred1

⋅

0.5

⋅

tred1

⋅

be2.1 tred1

⋅

0.5

⋅

be2.1

⋅

+

:=

Ssz1 1 cm

3

=

poło

ż

enie

ś

rodka ci

ęż

ko

ś

ci:

•

ys1

Ssz1

As1

:=

ys1 8.49 mm

⋅

=

b1.1

beff ys1

−

:=

b1.1 48.51 mm

⋅

=

zs1

Ssy1

As1

:=

zs1 4.18 mm

⋅

=

moment bezwładno

ś

ci:

•

Is1

be2.1 tred1

3

⋅

12

be2.1 tred1

⋅

zs1

( )

2

⋅

+

ceff1

( )

3

tred1

⋅

12

+

ceff1 tred1

⋅

0.5 ceff1

⋅

zs1

−

(

)

2

⋅

+

:=

Is1 0.33 cm

4

⋅

=

kf

0

:=

zginanie wzgl

ę

dem osi y-y oraz drugi pas rozci

ą

gany

sztywno

ść

translacyjna pasa:

•

K

1

E tred1

3

⋅

4 1

ν

2

−

(

)

1

b1.1

( )

2

hp

⋅

b1.1

( )

3

+

0.5 b1.1

⋅

b1.1

⋅

hp

⋅

kf

⋅

+

⋅

:=

napr

ęż

enie krytyczne dla usztywnie

ń

:

•

σ

cr.s1

2

K

1

E

⋅

Is1

⋅

⋅

As1

:=

σ

cr.s1

533.92 MPa

⋅

=

obliczenie współczynnika redukcyjnego z uwagi na wyboczenie dystorsyjne (1993-1-3 5.5.3.1)

•

λ

d1

fyb1

σ

cr.s1

:=

λ

d1

0.78

=

χ

d1

if

λ

d1

0.65

≤

1

,

if 0.65

λ

d1

<

1.38

≤

1.47

0.723

λ

d1

⋅

−

,

0.66

λ

d1

,













,













:=

χ

d1

0.9

=

Projektował: Artur Sta

ń

czewski

Strona 16

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

χ

d1

χ

d0

−

χ

d0

0.017

−

=

χ

d1

χ

d0

−

χ

d0

∆

<

1

=

mo

ż

na zako

ń

czy

ć

iteracje

Przyj

ę

to:

be2

be2.1

χ

d1

⋅

2.37 cm

=

:=

ceff

ceff1

χ

d1

⋅

1.54 cm

=

:=

tred

tred1

χ

d1

⋅

0.25 cm

=

:=

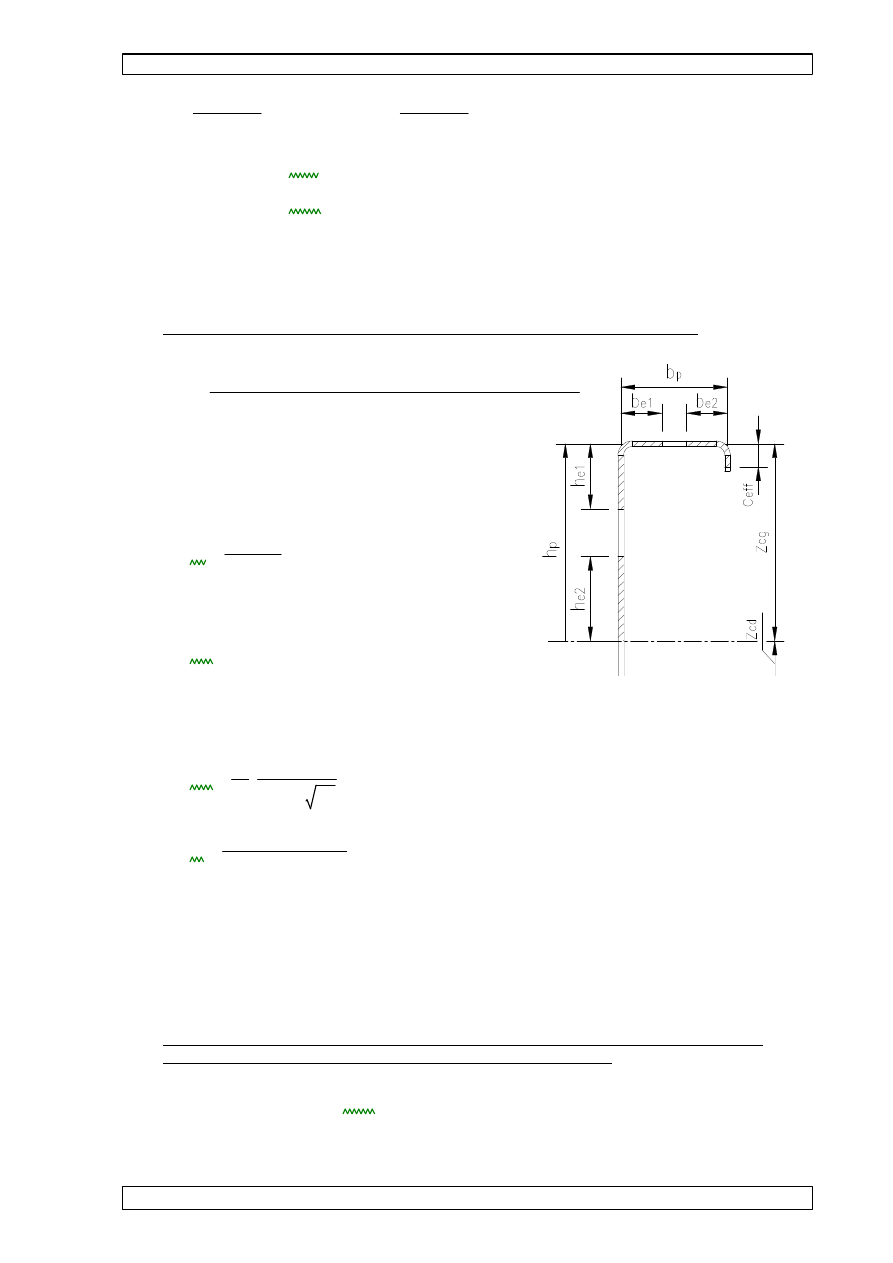
7.10.2

Ś

RODNIK PŁATWI.

7.10.2.1 WYZNACZENIE SZEROKO

Ś

CI WSPÓŁPRACUJ

Ą

CYCH he1 ORAZ he2.

zcg

cp hp 0.5 cp

⋅

−

(

)

⋅

t

⋅

bp hp

⋅

t

⋅

+

0.5 hp

2

⋅

t

⋅

+

ceff

2

0.5

⋅

tred

⋅

+

cp t

⋅

bp t

⋅

+

hp t

⋅

+

be1 t

⋅

+

be2 ceff

+

(

)

tred

⋅

+

:=

zcg 15.33 cm

⋅

=

zcd

hp zcg

−

14.37 cm

=

:=

stosunek napr

ęż

e

ń

na brzegach

ś

cianki

ψ

•

(1993-1-5 4.4 tab.4.1):

ψ

zcg hp

−

zcg

0.94

−

=

:=

parametr niestateczno

ś

ci miejscowej zale

ż

ny od

ψ

•

(1993-1-5 4.4 tab.4.1):

k

σ

7.81

6.29

ψ

⋅

−

9.78

ψ

2

⋅

+

22.31

=

:=

obliczenie współczynnika redukcyjnego (1993-1-5 4.4):

•

miarodajna szerkoko

ść

ś

cianki:

hp 297 mm

⋅

=

λ

p

hp

t

1

28.4

ε

⋅

k

σ

⋅

⋅

:=

λ

p

0.92

=

λ

p

0.673

>

ρ

λ

p

0.055 3

ψ

+

(

)

⋅

−

λ

p

2

:=

ρ

0.95

=

cz

ęść

współpracuj

ą

ca

ś

cianki (1993-1-5 4.4 tab.4.1):

•

heff

ρ

zcg

⋅

:=

heff 146.15 mm

⋅

=

he1

0.4 heff

⋅

:=

he1 58.46 mm

⋅

=

he1.0

he1

:=

he2

0.6 heff

⋅

:=

he2 87.69 mm

⋅

=

he2.0

he2

:=

7.10.2.2 WYZNACZENIE

Ś

RODKA CI

Ęś

KO

Ś

CI PRZEKROJU (przy zało

ż

eniu redukcji pasa,

usztywnienia i

ś

rodnika oraz przekroju brutto dolnej cz

ęś

ci ceownika).

pole przekroju:

•

As0

t cp bp

+

zcd

+

he2.0

+

he1.0

+

be1

+

(

)

⋅

tred be2 ceff

+

(

)

⋅

+

:=

As0 12.62 cm

2

⋅

=

Projektował: Artur Sta

ń

czewski

Strona 17

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

moment statyczny:

•

Ss0

cp t

⋅

0.5

⋅

cp

⋅

bp t

⋅

0.5

⋅

t

⋅

+

zcd t

⋅

0.5

⋅

zcd

⋅

+

he2.0 t

⋅

0.5 he2.0

⋅

zcd

+

(

)

⋅

he1.0 t

⋅

hp 0.5 he1.0

⋅

−

(

)

⋅

+

+

...

be1 t

⋅

hp

⋅

be2 tred

⋅

hp

⋅

+

ceff tred

⋅

hp 0.5 ceff

⋅

−

(

)

⋅

+

+

...

:=

Ss0 179.74 cm

3

⋅

=

poło

ż

enie

ś

rodka ci

ęż

ko

ś

ci:

•

zsd

Ss0

As0

14.24 cm

=

:=

zsg

hp zsd

−

15.46 cm

=

:=

moment bezwładno

ś

ci:

•

Is0

cp

3

t

⋅

12

cp t

⋅

zsd 0.5 cp

⋅

−

(

)

2

⋅

+

bp t

3

⋅

12

+

bp t

⋅

zsd 0.5 t

⋅

−

(

)

2

⋅

+

zsd

( )

3

t

⋅

12

+

zsd t

⋅

0.5 zsd

⋅

(

)

2

⋅

+

he2.0

(

)

3

t

⋅

12

he2.0 t

⋅

0.5 he2.0

⋅

(

)

2

⋅

+

he1.0

(

)

3

t

⋅

12

+

he1.0 t

⋅

zsg 0.5 he1.0

⋅

−

(

)

2

⋅

+

+

...

be1 t

3

⋅

12

be1 t

⋅

zsg 0.5 t

⋅

−

(

)

2

⋅

+

be2 tred

3

⋅

12

+

be2 tred

⋅

zsg 0.5 tred

⋅

−

(

)

2

⋅

+

+

...

ceff

3

tred

⋅

12

ceff tred

⋅

zsg 0.5 ceff

⋅

−

(

)

2

⋅

+

+

...

:=

Is0 1477.9 cm

4

⋅

=

zsd zcd

−

zcd

0.92

−

%

⋅

=

zsd zcd

−

zcd

∆

<

1

=

∆

5 %

⋅

=

mo

ż

na zako

ń

czy

ć

iteracje

7.10.3 PRZYJ

Ę

TE SZER. WSPÓŁPRACUJ

Ą

CE DLA USZTYWNIENIA, PÓLKI I

Ś

RODNIKA.

heff 146.15 mm

⋅

=

beff 57 mm

⋅

=

tred 2.46 mm

⋅

=

he1

he1.0 58.46mm

=

:=

be1 28.5 mm

⋅

=

ceff 15.4 mm

⋅

=

he2

he2.0 87.69mm

=

:=

be2 23.73 mm

⋅

=

7.11 CECHY GEOMETRYCZNE PRZEKROJU SPROWADZONEGO.

pole przekoju efektywnego:

•

Aeff

As0

:=

Aeff 12.62 cm

2

⋅

=

efektywny moment bezwładno

ś

ci:

•

Ieff.y

Is0

:=

Ieff.y 1477.9 cm

4

⋅

=

efektywne wska

ź

niki wytrzymało

ś

ci:

•

Weff.y.t

Ieff.y

zsd

:=

Weff.y.t 103.79 cm

3

⋅

=

Weff.y.c

Ieff.y

zsg

:=

Weff.y.c 95.59 cm

3

⋅

=

Weff.y

min Weff.y.t Weff.y.c

,

(

)

:=

Weff.y 95.59 cm

3

⋅

=

7.11 SPRAWDZENIE ZABEZPIECZENIA PŁATWI PRZED ZWICHRZENIEM (1993-1-3 10.1.1).

Projektował: Artur Sta

ń

czewski

Strona 18

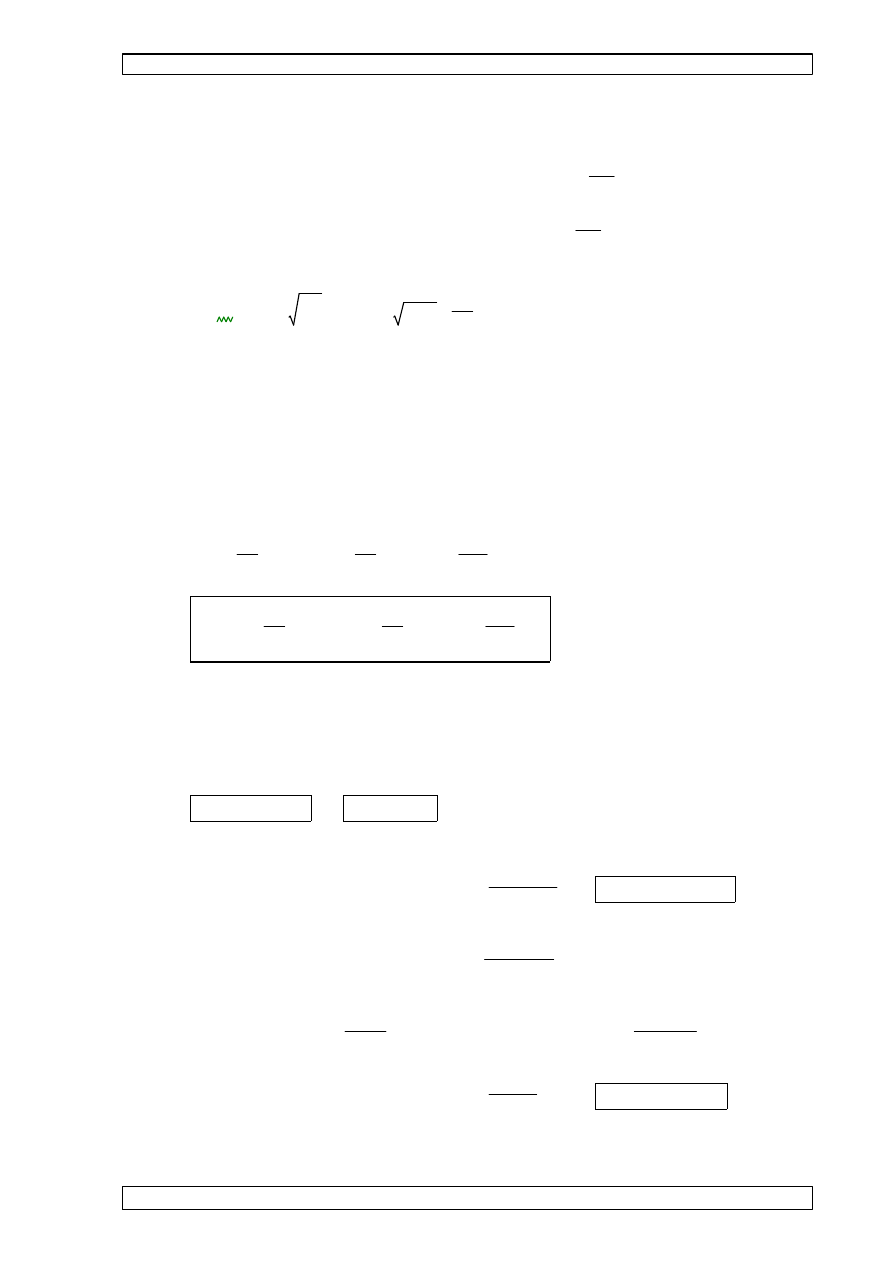
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

obliczenie sztywno

ś

ci na

ś

cinanie blachy trapezowej:

•

- obliczeniowa grubo

ść

poszycia:

tp

0.63

:=

- szeroko

ść

dachu:

broof

B

mm

:=

- rozstaw płatwi:

spl

ap

mm

:=

- wysoko

ść

profilu poszycia:

hw

55

:=

S

1000

tp

3

⋅

50

10

3

broof

⋅

+









⋅

spl

hw

⋅

N

⋅

:=

S

8443.36 kN

⋅

=

- rozpi

ę

to

ść

płatwi:

lp 6000 mm

⋅

=

- wysoko

ść

profilu płatwi:

hpl

300mm

:=

- wycinkowy moment bezwładno

ś

ci płatwi:

Iw 32770.4 cm

6

⋅

=

- moment bezwładno

ś

ci na skr

ę

canie:

It 0.39 cm

4

⋅

=

- moment bezwładno

ś

ci wzgl

ę

dem osi z-z:

Iz 53.23 cm

4

⋅

=

E Iw

⋅

π

2

lp

2

⋅

G It

⋅

+

E Iz

⋅

π

2

lp

2

⋅

0.25

⋅

hpl

2

⋅

+

















70

hpl

2

⋅

2247.73 kN

⋅

=

S

E Iw

⋅

π

2

lp

2

⋅

G It

⋅

+

E Iz

⋅

π

2

lp

2

⋅

0.25

⋅

hpl

2

⋅

+

















70

hpl

2

⋅

≥

1

=

- warunek spełniony

7.12 SPRAWDZENIE STANU GRANICZNEGO NO

Ś

NO

Ś

CI PŁATWI (1993-1-3 6.1.4).

7.12.1 SPRAWDZENIE SGN DLA KOMBINACJI OBCI

Ąś

E

Ń

MAX.

obliczeniowe momenty zginaj

ą

ce.

•

My.s 25.52 kNm

⋅

=

Mz.s 1 kNm

⋅

=

obliczenie no

ś

no

ś

ci na zginanie płatwi.

•

- no

ś

no

ść

wzgl

ę

dem osi y-y:

Mcy.Rd

Weff.y fyb

⋅

γ

M0

:=

Mcy.Rd 33.94 kNm

⋅

=

- no

ś

no

ść

wzgl

ę

dem osi z-z:

Mcz.Rd

Weff.z fya

⋅

γ

M0

=

k

5

:=

n

4

:=

fya

fyb

fu fyb

−

(

)

k n

⋅

t

2

⋅

A

⋅

+

:=

fya 375.48 MPa

⋅

=

fya

fu fyb

+

(

)

2

≤

1

=

Mcz.Rd

Wz fya

⋅

γ

M0

:=

Mcz.Rd 4.44 kNm

⋅

=

sprawdzenie warunku no

ś

no

ś

ci płatwi dla dwukierunkowego zginania:

•

Projektował: Artur Sta

ń

czewski

Strona 19

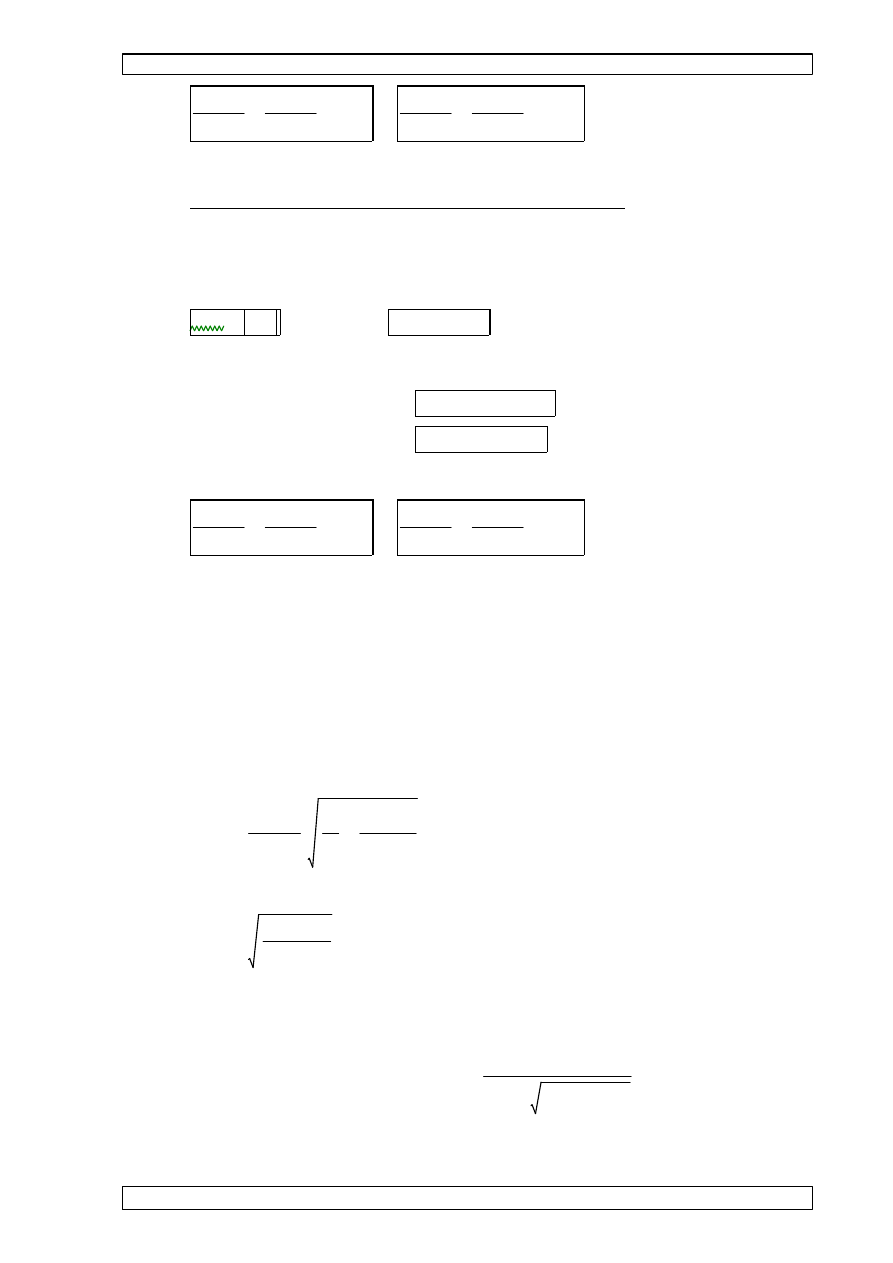
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

My.s

Mcy.Rd

Mz.s

Mcz.Rd

+

0.98

=

My.s

Mcy.Rd

Mz.s

Mcz.Rd

+

1

≤

1

=

sprawdzenie warunku no

ś

no

ś

ci płatwi na zwichrzenie (1993-1-3 p.6.2.4).

•

Zgodnie z pkt. 7.11 płatew jest zabezpieczona przed zwichrzeniem.

7.12.2 SPRAWDZENIE SGN DLA KOMBINACJI OBCI

Ąś

E

Ń

MIN.

obliczeniowe momenty zginaj

ą

ce.

•

My.i

My.i

:=

Mz.i 0.1 kNm

⋅

=

obliczenie no

ś

no

ś

ci na zginanie płatwi.

•

- no

ś

no

ść

wzgl

ę

dem osi y-y:

Mcy.Rd 33.94 kNm

⋅

=

- no

ś

no

ść

wzgl

ę

dem osi z-z:

Mcz.Rd 4.44 kNm

⋅

=

sprawdzenie warunku no

ś

no

ś

ci płatwi dla dwukierunkowego zginania:

•

My.i

Mcy.Rd

Mz.i

Mcz.Rd

+

0.47

=

My.i

Mcy.Rd

Mz.i

Mcz.Rd

+

1

≤

1

=

sprawdzenie warunku no

ś

no

ś

ci płatwi na wyboczenie (1993-1-1 p.6.3.2.2):

•

- moment krytyczny przy zwichrzeniu spr

ęż

ystym:

Lp

0.333 lp

⋅

:=

Mcr

π

2

E

⋅

Iz

⋅

Lp

2

Iw

Iz

Lp

2

G

⋅

It

⋅

π

2

E

⋅

Iz

⋅

+

⋅

:=

Mcr 69.2 kNm

⋅

=

- smukło

ść

wzgl

ę

dna przy zwichrzeniu:

λ

LT

Weff.y fyb

⋅

Mcr

:=

λ

LT

0.7

=

- parametr imperfekcji:

α

LT

0.34

:=

- dla krzywej "b"

- parametr krzywej zwichrzenia:

Φ

LT

0.5 1

α

LT

λ

LT

0.2

−

(

)

⋅

+

λ

LT

2

+









⋅

:=

Φ

LT

0.83

=

- współczynnik zwichrzenia:

χ

LT

1

Φ

LT

Φ

LT

2

λ

LT

2

−

+

:=

χ

LT

0.78

=

- wyznaczenie no

ś

no

ś

ci na wyboczenie płatwi:

Projektował: Artur Sta

ń

czewski

Strona 20

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

Mb.Rd

χ

LT Weff.y

⋅

fyb

γ

M1

⋅

:=

Mb.Rd 26.59 kNm

⋅

=

- warunek no

ś

no

ś

ci płatwi na zwichrzenie:

MEd

My.i

:=

MEd

Mb.Rd

0.57

=

MEd

Mb.Rd

1

≤

1

=

- warunek spełniony

7.12.3 SPRAWDZENIE WARUNKU NA NO

Ś

NO

ŚĆ

PŁATWI PRZY ZGINANIU I

Ś

CISKANIU

(1993-1-3 p. 6.1.9).

obliczeniowe siły przekrojowe w płatwi:

•

NEd

14.24kN

:=

(wg p.12 zał.B)

My.Ed

My.s

:=

Mz.Ed

Mz.s

:=

przesuni

ę

cie

ś

rodka ci

ęż

ko

ś

ci przekroju przy równomiernym

ś

ciskaniu:

•

Ss0z

cp t

⋅

0.5

⋅

bp

⋅

bp t

⋅

0.5

⋅

bp

⋅

+

be1 t

⋅

0.5

⋅

be1

⋅

+

be2 tred

⋅

bp 0.5 be2

⋅

−

(

)

⋅

+

ceff tred

⋅

bp

⋅

+

:=

Ss0z 12.37 cm

3

⋅

=

ysd

Ss0z

As0

:=

eNy

ygc ysd

−

:=

eNy 2.16 mm

⋅

=

eNz

zgc zsd

−

:=

eNz 6.1 mm

⋅

=

dodatkowe momenty powstałe w wyniku przesuni

ę

cia

ś

rodka ci

ęż

ko

ś

ci przekroju:

•

∆

My.Ed

NEd eNy

⋅

:=

∆

My.Ed 0.03 kNm

⋅

=

∆

Mz.Ed

NEd eNz

⋅

:=

∆

Mz.Ed 0.09 kNm

⋅

=

obliczenie no

ś

no

ś

ci przekroju na zginanie:

•

- wska

ź

niki wytrzymało

ś

ci odniesione do kraw

ę

dzi

ś

ciskanej:

Wy.com

Ieff.y

zsg

:=

Wy.com 95.59 cm

3

⋅

=

Wz.com

Iz

bp ysd

−

:=

Wz.com 11.28 cm

3

⋅

=

- wska

ź

niki wytrzymało

ś

ci odniesione do kraw

ę

dzi rozci

ą

ganej:

Wy.ten

Ieff.y

zsd

:=

Wy.ten 103.79 cm

3

⋅

=

Wz.ten

Iz

ysd

:=

Wz.ten 54.31 cm

3

⋅

=

- no

ś

no

ś

ci przekroju obliczeniowe przy zginaniu odniesione do kraw

ę

dzi

ś

ciskaniej:

Projektował: Artur Sta

ń

czewski

Strona 21

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

Mcy.Rd.com

Wy.com fyb

⋅

γ

M0

:=

Mcy.Rd.com 33.94 kNm

⋅

=

Mcz.Rd.com

Wz.com fyb

⋅

γ

M0

:=

Mcz.Rd.com 4 kNm

⋅

=

- no

ś

no

ś

ci przekroju obliczeniowe przy zginaniu odniesione do kraw

ę

dzi rozci

ą

ganej:

Mcy.Rd.ten

Wy.ten fyb

⋅

γ

M0

:=

Mcy.Rd.ten 36.84 kNm

⋅

=

Mcz.Rd.ten

Wz.ten fyb

⋅

γ

M0

:=

Mcz.Rd.ten 19.28 kNm

⋅

=

obliczenie no

ś

no

ś

ci przekroju na

ś

ciskanie:

•

Nc.Rd

Aeff fyb

⋅

γ

M0

:=

Nc.Rd 448.1 kN

⋅

=

sprawdzenie warunku no

ś

no

ś

ci:

•

Mcy.Rd.ten Mcy.Rd.com

≤

0

=

Mcz.Rd.ten Mcz.Rd.com

≤

0

=

- warunki niespełnione

NEd

Nc.Rd

My.Ed

∆

My.Ed

+

Mcy.Rd.com

+

Mz.Ed

∆

Mz.Ed

+

Mcz.Rd.com

+

1.06

=

NEd

Nc.Rd

My.Ed

∆

My.Ed

+

Mcy.Rd.com

+

Mz.Ed

∆

Mz.Ed

+

Mcz.Rd.com

+

1

≤

0

=

- warunek no

ś

no

ś

ci spełniony

7.12 SPRAWDZENIE STANU GRANICZNEGO U

ś

YTKOWALNO

Ś

CI PŁATWI.

obliczenie dopuszczalnego ugi

ę

cia płatwi:

•

wmax

lp

200

:=

wmax 30 mm

⋅

=

sprawdzenie ugi

ę

cia dla kombinacji max:

•

wz

5 ppks.y

⋅

lp

4

⋅

384 E

⋅

Ieff.y

⋅

:=

wz 20.75 mm

⋅

=

wy

0.75

5 ppks.z

⋅

Lp

4

⋅

384 E

⋅

Iz

⋅

⋅

:=

wy 0.33 mm

⋅

=

w

wz

2

wy

2

+

:=

w

20.76 mm

⋅

=

w

wmax

≤

1

=

- warunek spełniony

Projektował: Artur Sta

ń

czewski

Strona 22

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

sprawdzenie ugi

ę

cia dla kombinacji min (unoszenie):

•

wz

5 ppki.y

⋅

lp

4

⋅

384 E

⋅

Ieff.y

⋅

:=

wz

11.57

−

mm

⋅

=

wy

0.75

5 ppki.z

⋅

Lp

4

⋅

384 E

⋅

Iz

⋅

⋅

:=

wy 0.05 mm

⋅

=

w

wz

2

wy

2

+

:=

w

11.57 mm

⋅

=

w

wmax

≤

1

=

- warunek spełniony

WARUNKI STANU GRANICZNEGO NO

Ś

NO

Ś

CI I U

ś

YTKOWALNO

Ś

CI ZOSTAŁY SPEŁNIONE.

8. OBLICZENIA STATYCZNE KRATOWNICY DACHOWEJ.

UWAGA: Przypadek G1 (ci

ęż

ar własny) został wygenerowana automatycznie.

8.1 ZESTAWIENIE OBCI

Ąś

E

Ń

STAŁYCH - PRZYPADEK G2:

w

ę

zły po

ś

rednie:

•

G21

g1k g2k

+

g3k

+

g4k

+

(

)

ap

⋅

aw

⋅

g5k aw

⋅

+

:=

g4k

G21

kN

⋅

=

G21

w

ę

zły skrajne:

•

G22

G21 0.5

⋅

:=

G21

G22

kN

⋅

=

G22

w

ę

złeł kalenicowy:

•

G23

g1k g2k

+

g3k

+

g4k

+

(

)

ap

⋅

aw

⋅

2g5k aw

⋅

+

:=

g4k

G23

kN

⋅

=

G23

8.2 ZESTAWIENIE OBCI

Ąś

E

Ń

U

ś

YTKOWYCH - PRZYPADEK U1:

w

ę

zły po

ś

rednie:

•

Projektował: Artur Sta

ń

czewski

Strona 23

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

U11

qk ap

⋅

aw

⋅

:=

U11 6.15 kN

⋅

=

w

ę

zły skrajne:

•

U12

U11 0.5

⋅

:=

U12 3.07 kN

⋅

=

8.3 ZESTAWIENIE OBCI

Ąś

ENIA

Ś

NIEGIEM - PRZYPADKI S, SP, SL:

zestawienie dla równomiernego obci

ąż

enia

ś

niegiem (S) oraz połaci bardziej obci

ąż

onej dla

•

przypadków SP i SL:

- w

ę

zły po

ś

rednie:

S1

s cos

α

p

( )

⋅

ap

⋅

aw

⋅

:=

S1 14.69 kN

⋅

=

- w

ę

zły po

ś

rednie:

S2

s cos

α

p

( )

⋅

0.5

⋅

ap aw

⋅

:=

S2 7.34 kN

⋅

=

zestawienie dla nierównomiernego obci

ąż

enia

ś

niegiem (SP, SL) -poła

ć

mniej obci

ąż

ona:

•

- w

ę

zły po

ś

renie:

S1PL

0.5s cos

α

p

( )

⋅

ap

⋅

aw

⋅

:=

S1PL 7.34 kN

⋅

=

- w

ę

zły skrajne:

S2PL

0.5s cos

α

p

( )

⋅

0.5

⋅

ap aw

⋅

:=

S2PL 3.67 kN

⋅

=

- w

ę

złeł kalenicowy:

S3PL

0.5s cos

α

p

( )

⋅

0.5

⋅

ap aw

⋅

s cos

α

p

( )

⋅

0.5

⋅

ap aw

⋅

+

...

:=

S3PL 11.02 kN

⋅

=

8.4 ZESTAWIENIE OBCI

Ąś

ENIA WIATREM - PRZYPADKI WP i WL (wiatr z boku):

poła

ć

nawietrzna:

•

- w

ę

zeł skrajny przy okapie

WPL

1

wF 0.5

⋅

ap

⋅

0.5

⋅

aw

⋅

wG 0.5

⋅

ap

⋅

0.5

⋅

aw

⋅

+

:=

WPL

1

9.14

−

kN

⋅

=

- w

ę

zeł przedskrajny przy okapie

WPL

2

wF 0.5

⋅

ap

⋅

0.5

⋅

aw

⋅

wG 0.5

⋅

ap

⋅

0.5

⋅

aw

⋅

+

wH 0.5

⋅

ap aw

⋅

+

:=

WPL

2

13.57

−

kN

⋅

=

- w

ę

zeł po

ś

redni

WPL

3

wH ap

⋅

aw

⋅

:=

WPL

3

8.86

−

kN

⋅

=

- w

ę

zeł skrajny w kalenicy

WPL

4

wH 0.5

⋅

ap

⋅

aw

⋅

:=

WPL

4

4.43

−

kN

⋅

=

poła

ć

zawietrzna:

•

- w

ę

zeł po

ś

redni

WPL

5

wI ap

⋅

aw

⋅

:=

WPL

5

8.86

−

kN

⋅

=

- w

ę

zeł skrajny

WPL

6

wI 0.5

⋅

ap

⋅

aw

⋅

:=

WPL

6

4.43

−

kN

⋅

=

Projektował: Artur Sta

ń

czewski

Strona 24

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

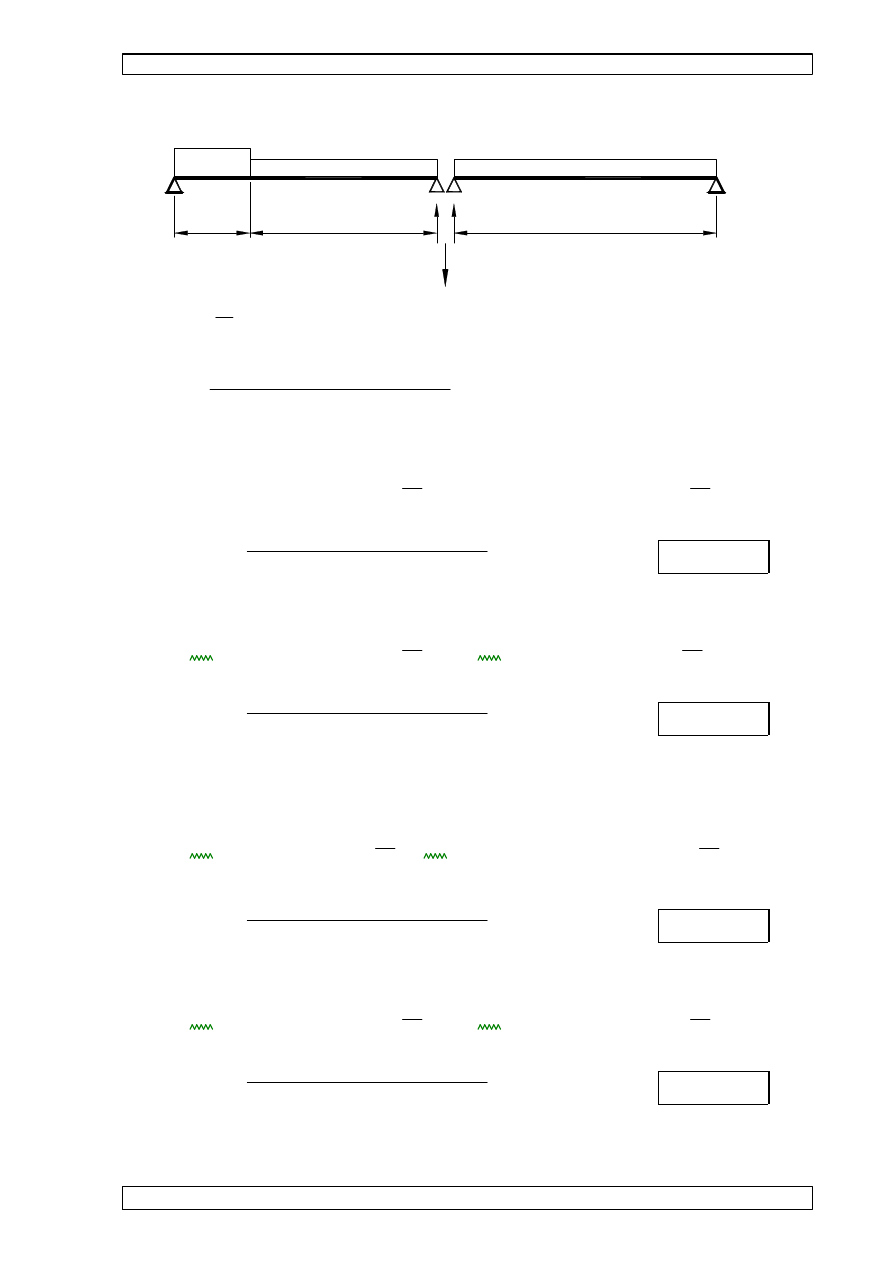
8.5 ZESTAWIENIE OBCI

Ąś

ENIA WIATREM - PRZYPADEK WB (wiatr z przodu):

l

p1

l

p2

l

p

R

L

R

P

R

q

1

q

1

q

2

lp1

e

10

:=

lp2

lp lp1

−

:=

lp 6 m

=

RL

0.5q2 lp1

2

⋅

q1 0.5 lp2

2

⋅

lp1 lp2

⋅

+









⋅

+

lp1 lp2

+

=

RP 0.5 q1

⋅

lp

⋅

=

R

RL RP

+

=

w

ę

zły skrajne przy okapie:

•

q1

wH 0.5

⋅

ap

⋅

:=

q1

0.74

−

kN

m

⋅

=

q2

wF 0.5

⋅

ap

⋅

:=

q2

1.75

−

kN

m

⋅

=

WB

1

0.5q2 lp1

2

⋅

q1 0.5 lp2

2

⋅

lp1 lp2

⋅

+









⋅

+

lp1 lp2

+

0.5 q1

⋅

lp

⋅

+

:=

WB

1

4.88

−

kN

⋅

=

w

ę

zły po

ś

rednie (F):

•

q1

wH ap

⋅

:=

q1

1.48

−

kN

m

⋅

=

q2

wF ap

⋅

:=

q2

3.5

−

kN

m

⋅

=

WB

2

0.5q2 lp1

2

⋅

q1 0.5 lp2

2

⋅

lp1 lp2

⋅

+









⋅

+

lp1 lp2

+

0.5 q1

⋅

lp

⋅

+

:=

WB

2

9.75

−

kN

⋅

=

w

ę

zły po

ś

rednie (FG):

•

q1

wH ap

⋅

:=

q1

1.48

−

kN

m

⋅

=

q2

wF 0.5

⋅

ap wG 0.5

⋅

ap

+

:=

q2

3.05

−

kN

m

⋅

=

WB

3

0.5q2 lp1

2

⋅

q1 0.5 lp2

2

⋅

lp1 lp2

⋅

+









⋅

+

lp1 lp2

+

0.5 q1

⋅

lp

⋅

+

:=

WB

3

9.55

−

kN

⋅

=

w

ę

zły po

ś

rednie (G):

•

q1

wH ap

⋅

:=

q1

1.48

−

kN

m

⋅

=

q2

wG ap

⋅

:=

q2

2.59

−

kN

m

⋅

=

WB

4

0.5q2 lp1

2

⋅

q1 0.5 lp2

2

⋅

lp1 lp2

⋅

+









⋅

+

lp1 lp2

+

0.5 q1

⋅

lp

⋅

+

:=

WB

4

9.35

−

kN

⋅

=

w

ę

zły skrajne w kalenicy:

•

Projektował: Artur Sta

ń

czewski

Strona 25

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

q1

wH 0.5

⋅

ap

:=

q1

0.74

−

kN

m

⋅

=

q2

wG 0.5

⋅

ap

:=

q2

1.3

−

kN

m

⋅

=

WB

5

0.5q2 lp1

2

⋅

q1 0.5 lp2

2

⋅

lp1 lp2

⋅

+









⋅

+

lp1 lp2

+

0.5 q1

⋅

lp

⋅

+

:=

WB

5

4.67

−

kN

⋅

=

8.5 WYNIKI OBLICZE

Ń

STATYCZNYCH.

SZCZEGÓŁOWE WYNIKI OBLICZE

Ń

ZAMIESZCZONO W ZAŁ

Ą

CZNIKU A.

9. WYMIAROWANIE PR

Ę

TÓW KRATOWNICY DACHOWEJ.

9.1 WYMIAROWANIE PASA GÓRNEGO.

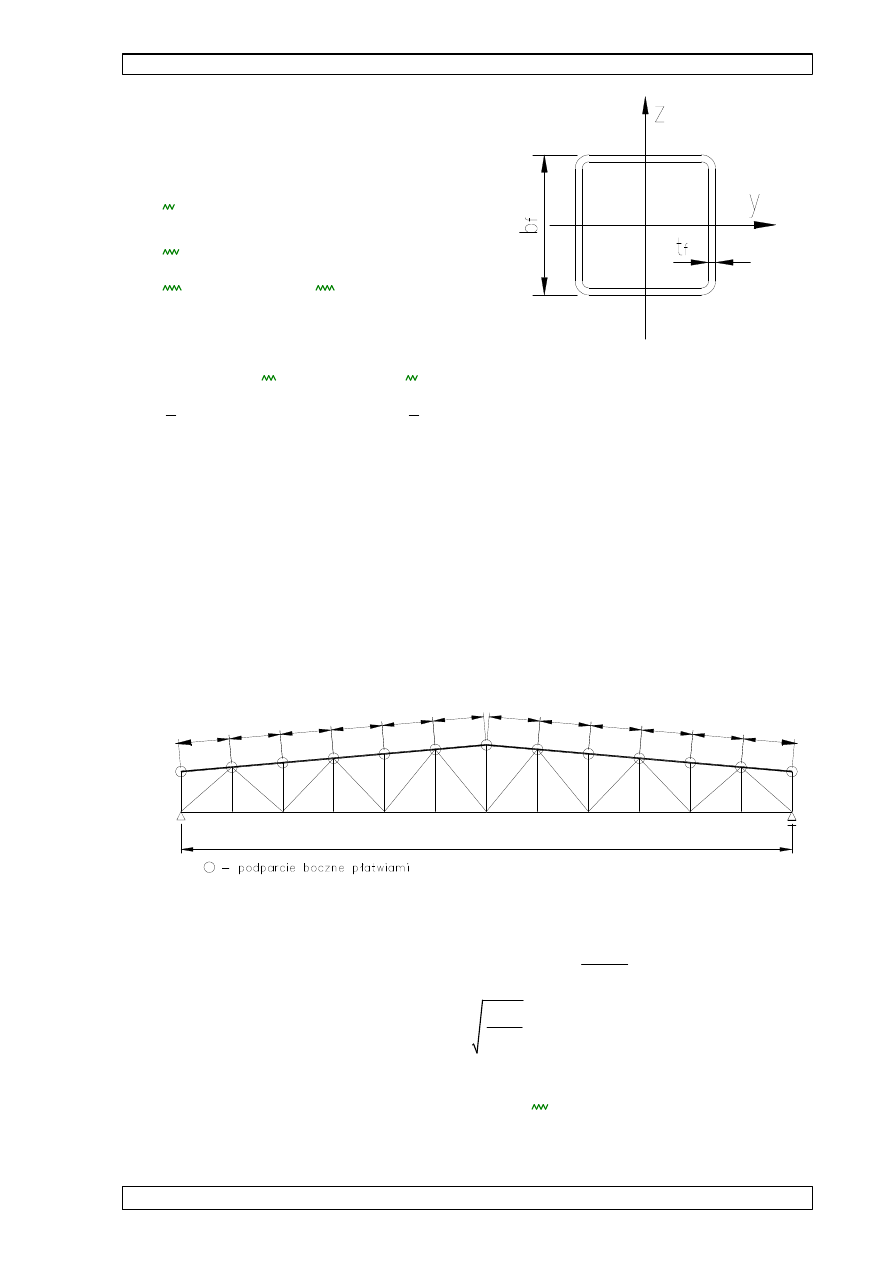
9.1.1 CHARAKTERYSTYKI PRZEKROJU RK 100x100x4:

Projektował: Artur Sta

ń

czewski

Strona 26

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

bf

100mm

:=

tf

4mm

:=

r

1.6 tf

⋅

:=

A

14.95cm

2

:=

Iy

226.35cm

4

:=

Iz

Iy

:=

9.1.2 SPRAWDZENIE KLASY PRZEKROJU:

ε

0.81

=

c

bf 2tf

−

:=

t

tf

:=

c

t

23

=

33

ε

26.85

=

c

t

33

ε

≤

1

=

- klasa 1

9.1.3 EKSTREMALNE SIŁY W PASIE GÓRNYM:

maksymalna siła

ś

ciskaj

ą

ca:

•

NEd.c

366.07kN

:=

siła

ś

ciskaj

ą

ca od t

ęż

nika:

•

Nst.c

26.75kN

:=

wg pkt.12.4

maksymalna siła rozci

ą

gaj

ą

ca:

•

NEd.t

58.79kN

:=

9.1.4 SPRAWDZENIE NO

Ś

NO

Ś

CI NA WYBOCZENIE:

- dłudo

ść

teoretyczna pr

ę

ta mi

ę

dzy w

ę

złami:

lt

ap

:=

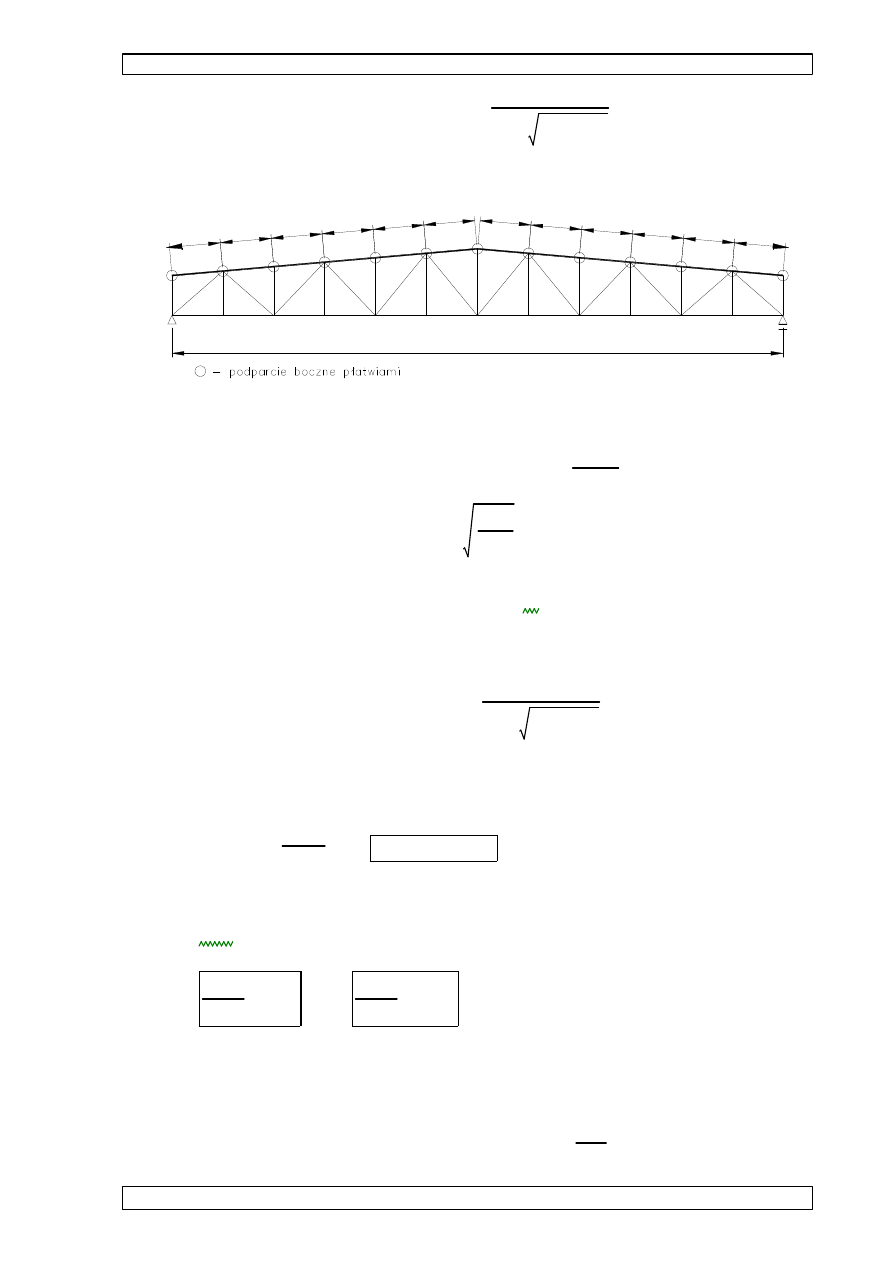
wyboczenie w płaszczy

ź

nie kratownicy:

•

l

t

B=23000

l

t

l

t

l

t

l

t

l

t

l

t

l

t

l

t

l

t

l

t

l

t

- obliczeniowa długo

ść

wyboczeniowa:

Lcr.y

1.0lt

:=

Lcr.y 2562.31 mm

⋅

=

- siła krytyczna przy wyboczeniu:

Ncr.y

π

2

E Iy

⋅

Lcr.y

2

:=

Ncr.y 714.56 kN

⋅

=

- smukło

ść

wzgl

ę

dna y-y:

λ

y

A fy

⋅

Ncr.y

:=

λ

y

0.86

=

- parametr imperfekcji:

dla krzywej "c"

α

0.49

:=

- parametr krzywej wyboczenia:

Φ

y

0.5 1

α λ

y

0.2

−

(

)

⋅

+

λ

y

2

+









⋅

:=

Projektował: Artur Sta

ń

czewski

Strona 27

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

- współczynnik wyboczeniowy:

χ

y

1

Φ

y

Φ

y

2

λ

y

2

−

+

:=

χ

y

0.62

=

wyboczenie z płaszczyzny kratownicy:

•

l

t

B=23000

l

t

l

t

l

t

l

t

l

t

l

t

l

t

l

t

l

t

l

t

l

t

- obliczeniowa długo

ść

wyboczeniowa:

Lcr.z

1.0lt

:=

Lcr.z 2562.31 mm

⋅

=

- siła krytyczna przy wyboczeniu:

Ncr.z

π

2

E Iz

⋅

Lcr.y

2

:=

Ncr.z 714.56 kN

⋅

=

- smukło

ść

wzgl

ę

dna y-y:

λ

z

A fy

⋅

Ncr.z

:=

λ

z

0.86

=

- parametr imperfekcji:

dla krzywej "c"

α

0.49

:=

- parametr krzywej wyboczenia:

Φ

z

0.5 1

α λ

z

0.2

−

(

)

⋅

+

λ

z

2

+









⋅

:=

- współczynnik wyboczeniowy:

χ

z

1

Φ

z

Φ

z

2

λ

z

2

−

+

:=

χ

z

0.62

=

no

ś

no

ść

elementu na wyboczenie:

•

χ

min

χ

y

χ

z

,

(

)

:=

χ

0.62

=

Nb.Rd

χ

A

⋅

fy

⋅

γ

M1

:=

Nb.Rd 330.88 kN

⋅

=

warunek no

ś

no

ś

ci:

•

NEd

NEd.c Nst.c

+

:=

NEd 392.82 kN

⋅

=

NEd

Nb.Rd

1.19

=

NEd

Nb.Rd

1

≤

0

=

- warunek spełniony

9.1.5 SPRAWDZENIE NO

Ś

NO

Ś

CI NA ROZCI

Ą

GANIE:

no

ś

no

ść

przekroju na rozci

ą

ganie:

•

Nt.Rd

A fy

⋅

γ

M0

:=

Nt.Rd 530.73 kN

⋅

=

Projektował: Artur Sta

ń

czewski

Strona 28

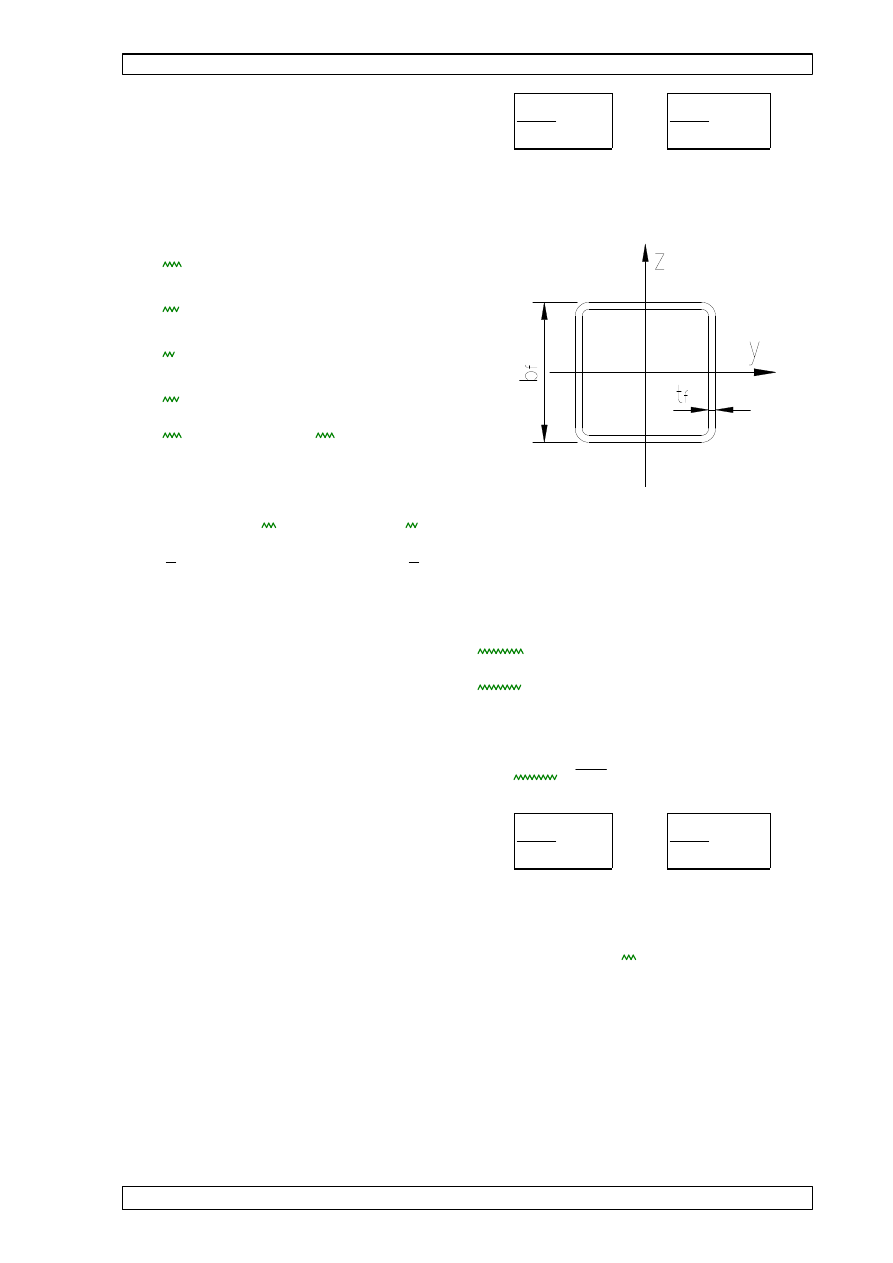
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

warunek no

ś

no

ś

ci:

•

NEd.t

Nt.Rd

0.11

=

NEd.t

Nt.Rd

1

≤

1

=

9.2 WYMIAROWANIE PASA DOLNEGO.

9.2.1 CHARAKTERYSTYKI PRZEKROJU RK 90x90x4:

bf

90mm

:=

tf

4mm

:=

r

1.6 tf

⋅

:=

A

13.35cm

2

:=

Iy

161.92cm

4

:=

Iz

Iy

:=

9.2.2 SPRAWDZENIE KLASY PRZEKROJU:

ε

0.81

=

c

bf 2tf

−

:=

t

tf

:=

c

t

20.5

=

33

ε

26.85

=

c

t

33

ε

≤

1

=

- klasa 1

9.2.3 EKSTREMALNE SIŁY W PASIE DOLNYM:

maksymalna siła

ś

ciskaj

ą

ca:

•

NEd.c

54.84kN

:=

maksymalna siła rozci

ą

gaj

ą

ca:

•

NEd.t

370.62kN

:=

9.2.4 SPRAWDZENIE NO

Ś

NO

Ś

CI NA ROZCI

Ą

GANIE:

no

ś

no

ść

przekroju na rozci

ą

ganie:

•

Nt.Rd

A fy

⋅

γ

M0

:=

Nt.Rd 473.93 kN

⋅

=

warunek no

ś

no

ś

ci:

•

NEd.t

Nt.Rd

0.78

=

NEd.t

Nt.Rd

1

≤

1

=

9.2.5 SPRAWDZENIE NO

Ś

NO

Ś

CI NA WYBOCZENIE:

- dłudo

ść

teoretyczna pr

ę

ta mi

ę

dzy w

ę

złami:

lt

apr

:=

wyboczenie w płaszczy

ź

nie kratownicy:

•

Projektował: Artur Sta

ń

czewski

Strona 29

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

B=23000

3*l

t

3*l

t

3*l

t

3*l

t

l

t

l

t

l

t

l

t

- obliczeniowa długo

ść

wyboczeniowa:

Lcr.y

1.0lt

:=

Lcr.y 2550 mm

⋅

=

- siła krytyczna przy wyboczeniu:

Ncr.y

π

2

E Iy

⋅

Lcr.y

2

:=

Ncr.y 516.11 kN

⋅

=

- smukło

ść

wzgl

ę

dna y-y:

λ

y

A fy

⋅

Ncr.y

:=

λ

y

0.96

=

- parametr imperfekcji:

dla krzywej "c"

α

0.49

:=

- parametr krzywej wyboczenia:

Φ

y

0.5 1

α λ

y

0.2

−

(

)

⋅

+

λ

y

2

+









⋅

:=

- współczynnik wyboczeniowy:

χ

y

1

Φ

y

Φ

y

2

λ

y

2

−

+

:=

χ

y

0.56

=

wyboczenie z płaszczyzny kratownicy:

•

- obliczeniowa długo

ść

wyboczeniowa:

Lcr.z

3lt

:=

Lcr.z 7650 mm

⋅

=

- siła krytyczna przy wyboczeniu:

Ncr.z

π

2

E Iz

⋅

Lcr.z

2

:=

Ncr.z 57.35 kN

⋅

=

- smukło

ść

wzgl

ę

dna y-y:

λ

z

A fy

⋅

Ncr.z

:=

λ

z

2.87

=

- parametr imperfekcji:

dla krzywej "c"

α

0.49

:=

- parametr krzywej wyboczenia:

Φ

z

0.5 1

α λ

z

0.2

−

(

)

⋅

+

λ

z

2

+









⋅

:=

- współczynnik wyboczeniowy:

χ

z

1

Φ

z

Φ

z

2

λ

z

2

−

+

:=

χ

z

0.1

=

no

ś

no

ść

elementu na wyboczenie:

•

Projektował: Artur Sta

ń

czewski

Strona 30

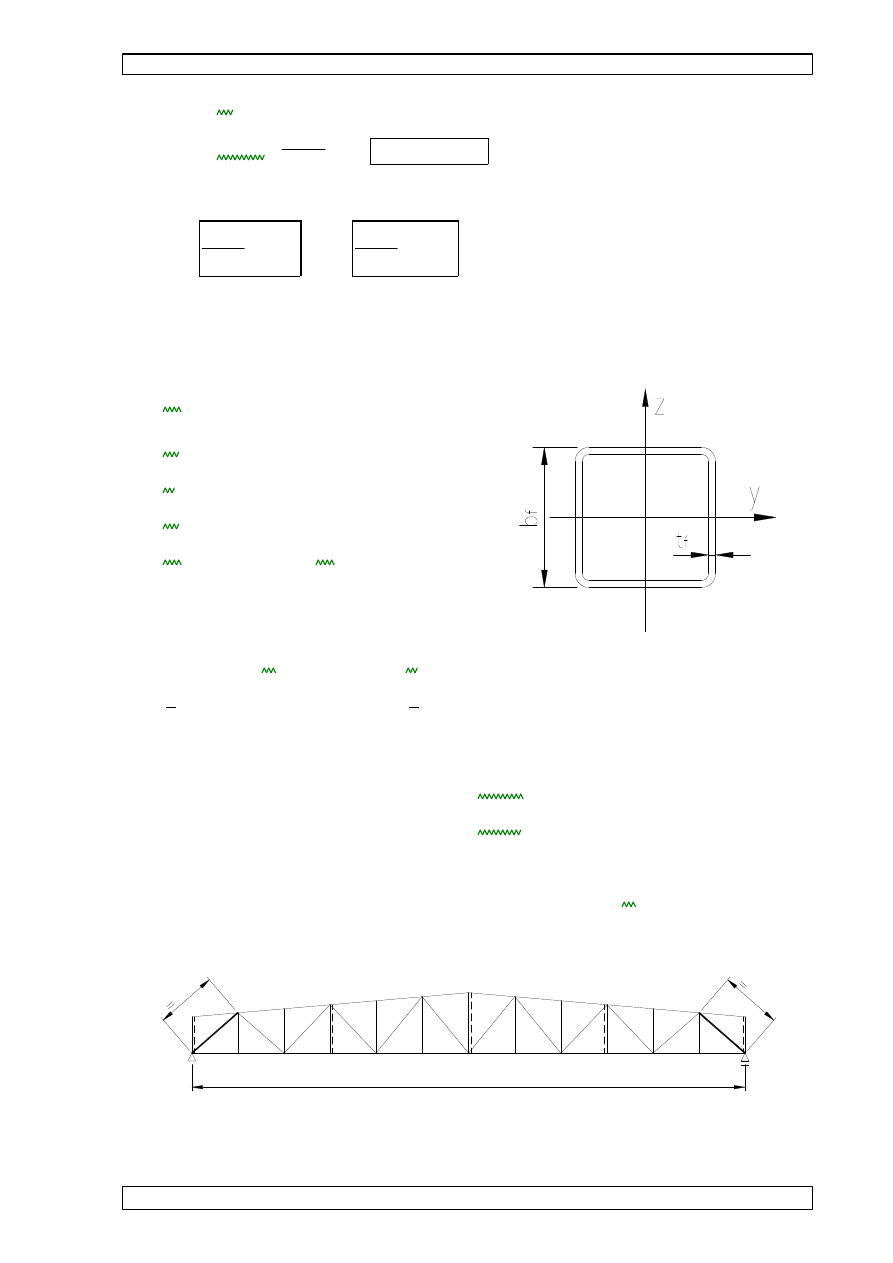
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

χ

min

χ

y

χ

z

,

(

)

:=

χ

0.1

=

Nb.Rd

χ

A

⋅

fy

⋅

γ

M1

:=

Nb.Rd 48.73 kN

⋅

=

warunek no

ś

no

ś

ci:

•

NEd.c

Nb.Rd

1.13

=

NEd.c

Nb.Rd

1

≤

0

=

- warunek spełniony

9.3 WYMIAROWANIE KRZY

ś

ULCÓW PODPOROWYCH.

9.3.1 CHARAKTERYSTYKI PRZEKROJU RK 90x90x4:

bf

90mm

:=

tf

4mm

:=

r

1.6 tf

⋅

:=

A

13.35cm

2

:=

Iy

161.92cm

4

:=

Iz

Iy

:=

I

min Iy Iz

,

( )

:=

9.3.2 SPRAWDZENIE KLASY PRZEKROJU:

ε

0.81

=

c

bf 2tf

−

:=

t

tf

:=

c

t

20.5

=

33

ε

26.85

=

c

t

33

ε

≤

1

=

- klasa 1

9.3.3 EKSTREMALNE SIŁY W PR

Ę

TACH:

maksymalna siła

ś

ciskaj

ą

ca:

•

NEd.c

215.76kN

:=

maksymalna siła rozci

ą

gaj

ą

ca:

•

NEd.t

35.82kN

:=

9.3.4 SPRAWDZENIE NO

Ś

NO

Ś

CI NA WYBOCZENIE:

- dłudo

ść

teoretyczna pr

ę

ta mi

ę

dzy w

ę

złami:

lt

2.54m

:=

wyboczenie w płaszczy

ź

nie i z płaszczyzny kratownicy:

•

B=23000

l

t

2.

54

m

l

t

2.5

4m

Projektował: Artur Sta

ń

czewski

Strona 31

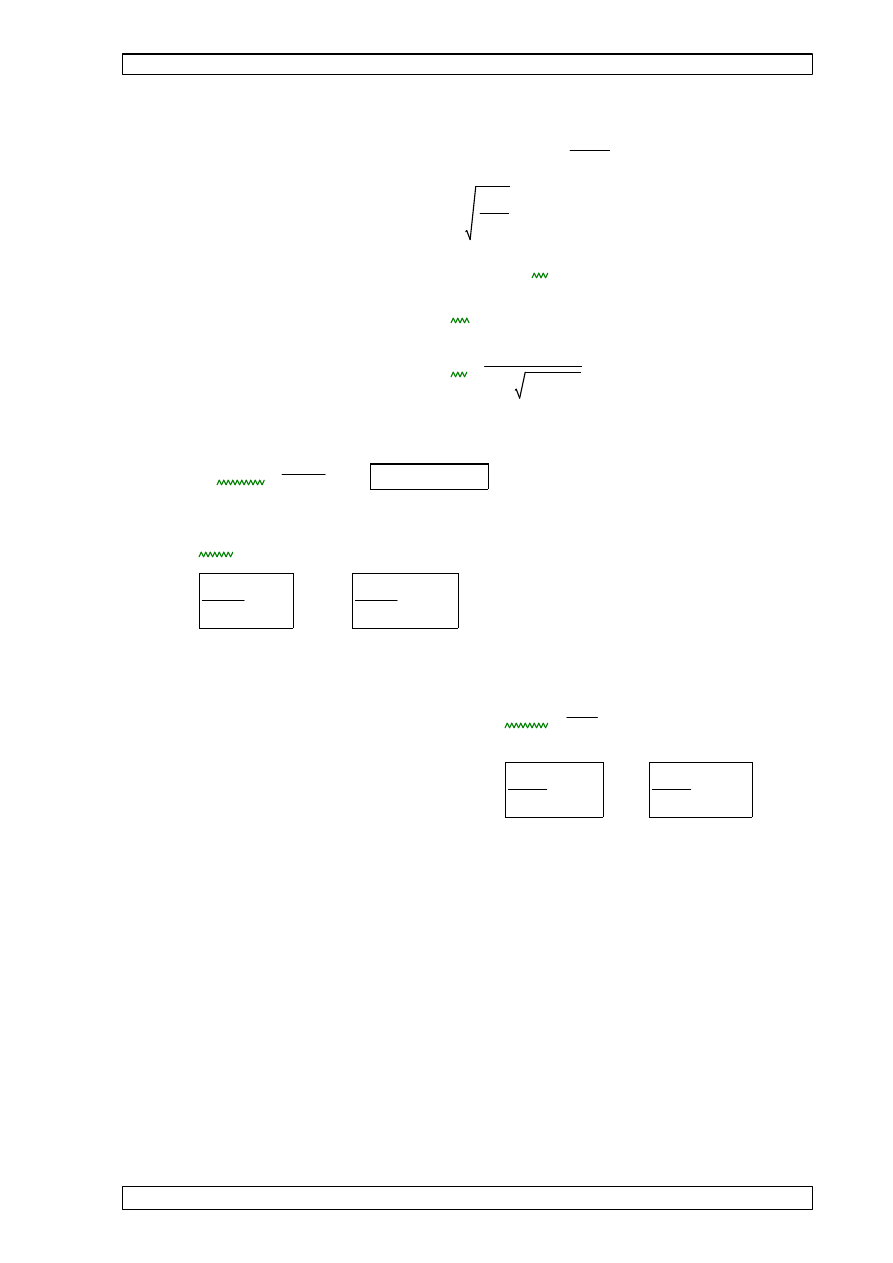
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

- obliczeniowa długo

ść

wyboczeniowa:

Lcr

1.0lt

:=

Lcr 2540 mm

⋅

=

- siła krytyczna przy wyboczeniu:

Ncr

π

2

E I

⋅

Lcr

2

:=

Ncr 520.18 kN

⋅

=

- smukło

ść

wzgl

ę

dna y-y:

λ

A fy

⋅

Ncr

:=

λ

0.95

=

- parametr imperfekcji:

dla krzywej "c"

α

0.49

:=

- parametr krzywej wyboczenia:

Φ

0.5 1

α λ

0.2

−

(

)

⋅

+

λ

2

+





⋅

:=

- współczynnik wyboczeniowy:

χ

1

Φ

Φ

2

λ

2

−

+

:=

χ

0.57

=

no

ś

no

ść

elementu na wyboczenie:

•

Nb.Rd

χ

A

⋅

fy

⋅

γ

M1

:=

Nb.Rd 268.6 kN

⋅

=

warunek no

ś

no

ś

ci:

•

NEd

NEd.c

:=

NEd 215.76 kN

⋅

=

NEd

Nb.Rd

0.8

=

NEd

Nb.Rd

1

≤

1

=

- warunek spełniony

9.3.5 SPRAWDZENIE NO

Ś

NO

Ś

CI NA ROZCI

Ą

GANIE:

no

ś

no

ść

przekroju na rozci

ą

ganie:

•

Nt.Rd

A fy

⋅

γ

M0

:=

Nt.Rd 473.93 kN

⋅

=

warunek no

ś

no

ś

ci:

•

NEd.t

Nt.Rd

0.08

=

NEd.t

Nt.Rd

1

≤

1

=

9.4 WYMIAROWANIE KRZY

ś

ULCÓW - pr

ę

ty 26, 27, 34, 35.

Projektował: Artur Sta

ń

czewski

Strona 32

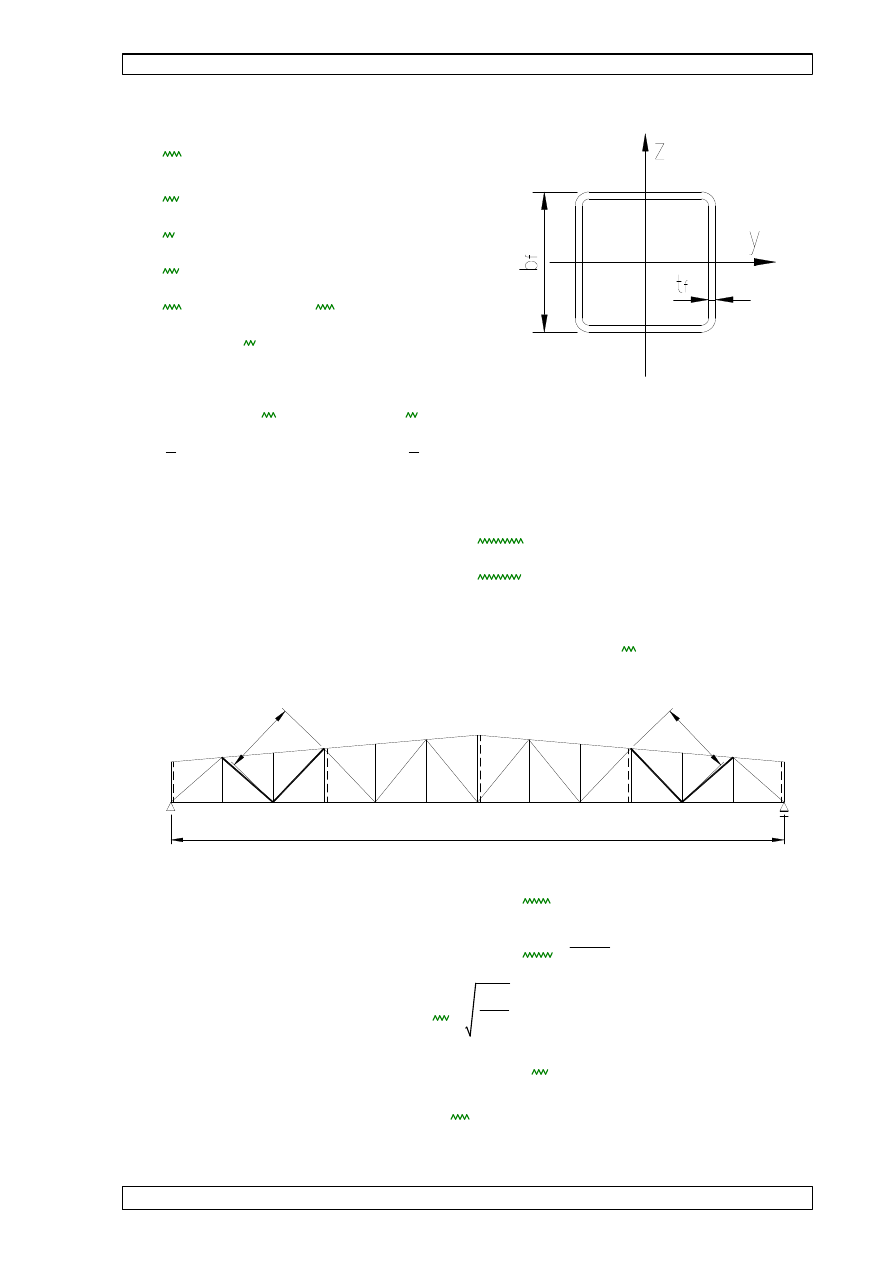
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

9.4.1 CHARAKTERYSTYKI PRZEKROJU RK 63.5x63.5x4:

bf

63.5mm

:=

tf

4mm

:=

r

1.6 tf

⋅

:=

A

9.11cm

2

:=

Iy

52.47cm

4

:=

Iz

Iy

:=

I

min Iy Iz

,

( )

:=

9.4.2 SPRAWDZENIE KLASY PRZEKROJU:

ε

0.81

=

c

bf 2tf

−

:=

t

tf

:=

c

t

13.88

=

33

ε

26.85

=

c

t

33

ε

≤

1

=

- klasa 1

9.4.3 EKSTREMALNE SIŁY W PR

Ę

TACH:

maksymalna siła

ś

ciskaj

ą

ca:

•

NEd.c

92.55kN

:=

maksymalna siła rozci

ą

gaj

ą

ca:

•

NEd.t

140.94kN

:=

9.4.4 SPRAWDZENIE NO

Ś

NO

Ś

CI NA WYBOCZENIE:

- dłudo

ść

teoretyczna pr

ę

ta mi

ę

dzy w

ę

złami:

lt

2.77m

:=

wyboczenie w płaszczy

ź

nie i z płaszczyzny kratownicy:

•

B=23000

2.7

7m

2.

77

m

- obliczeniowa długo

ść

wyboczeniowa:

Lcr

1.0lt

:=

Lcr 2770 mm

⋅

=

- siła krytyczna przy wyboczeniu:

Ncr

π

2

E I

⋅

Lcr

2

:=

Ncr 141.73 kN

⋅

=

- smukło

ść

wzgl

ę

dna y-y:

λ

A fy

⋅

Ncr

:=

λ

1.51

=

- parametr imperfekcji:

dla krzywej "c"

α

0.49

:=

- parametr krzywej wyboczenia:

Φ

0.5 1

α λ

0.2

−

(

)

⋅

+

λ

2

+





⋅

:=

Projektował: Artur Sta

ń

czewski

Strona 33

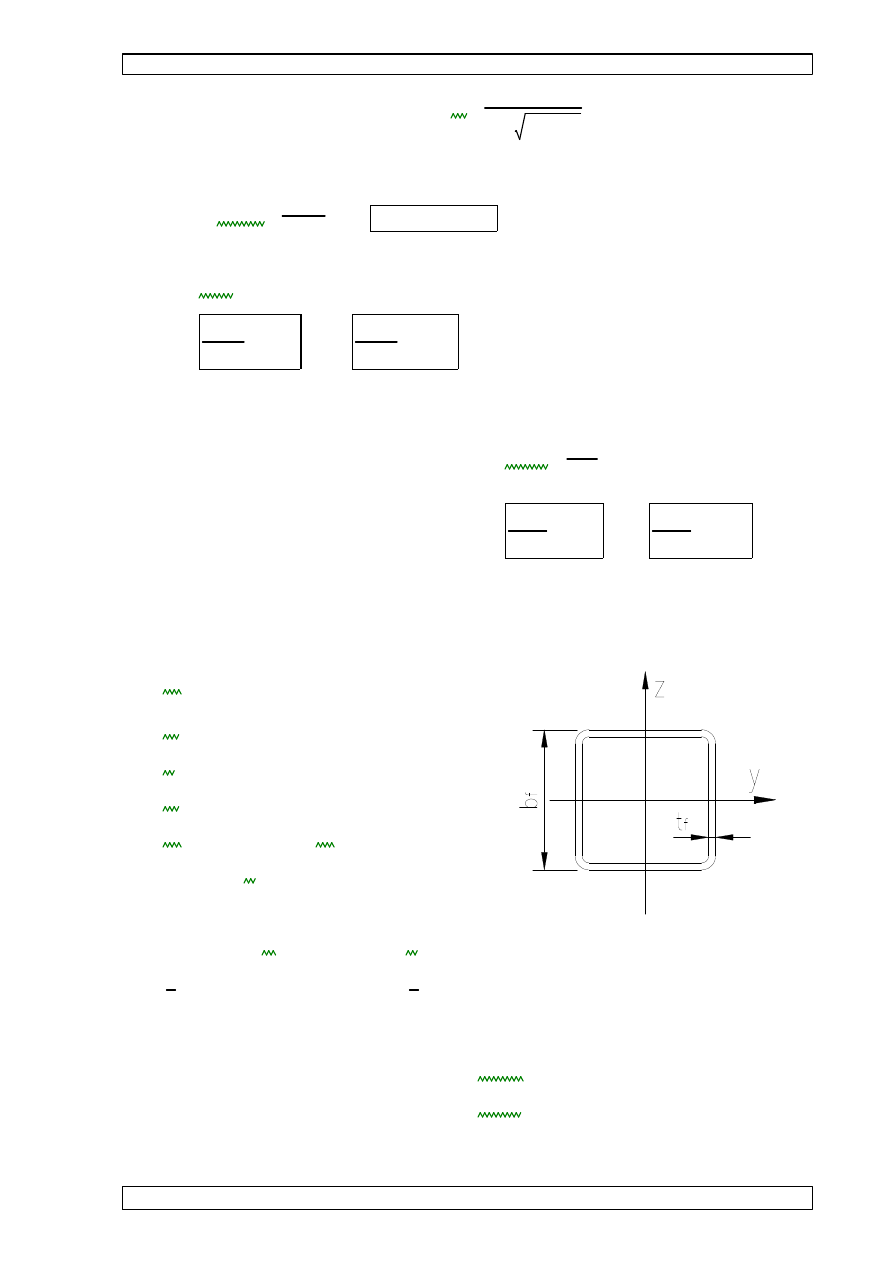
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

- współczynnik wyboczeniowy:

χ

1

Φ

Φ

2

λ

2

−

+

:=

χ

0.31

=

no

ś

no

ść

elementu na wyboczenie:

•

Nb.Rd

χ

A

⋅

fy

⋅

γ

M1

:=

Nb.Rd 100.62 kN

⋅

=

warunek no

ś

no

ś

ci:

•

NEd

NEd.c

:=

NEd 92.55 kN

⋅

=

NEd

Nb.Rd

0.92

=

NEd

Nb.Rd

1

≤

1

=

- warunek spełniony

9.4.5 SPRAWDZENIE NO

Ś

NO

Ś

CI NA ROZCI

Ą

GANIE:

no

ś

no

ść

przekroju na rozci

ą

ganie:

•

Nt.Rd

A fy

⋅

γ

M0

:=

Nt.Rd 323.4 kN

⋅

=

warunek no

ś

no

ś

ci:

•

NEd.t

Nt.Rd

0.44

=

NEd.t

Nt.Rd

1

≤

1

=

9.4 WYMIAROWANIE POZOSTAŁYCH KRZY

ś

ULCÓW I SŁUPKÓW.

9.4.1 CHARAKTERYSTYKI PRZEKROJU RK 50x50x4:

bf

50mm

:=

tf

4mm

:=

r

1.6 tf

⋅

:=

A

6.95cm

2

:=

Iy

23.74cm

4

:=

Iz

Iy

:=

I

min Iy Iz

,

( )

:=

9.4.2 SPRAWDZENIE KLASY PRZEKROJU:

ε

0.81

=

c

bf 2tf

−

:=

t

tf

:=

c

t

10.5

=

33

ε

26.85

=

c

t

33

ε

≤

1

=

- klasa 1

9.4.3 EKSTREMALNE SIŁY W PR

Ę

TACH:

maksymalna siła

ś

ciskaj

ą

ca:

•

NEd.c

35.76kN

:=

- pr

ę

ty 30, 31

maksymalna siła rozci

ą

gaj

ą

ca:

•

NEd.t

45.51kN

:=

- pr

ę

ty 28, 33

9.4.4 SPRAWDZENIE NO

Ś

NO

Ś

CI NA WYBOCZENIE:

Projektował: Artur Sta

ń

czewski

Strona 34

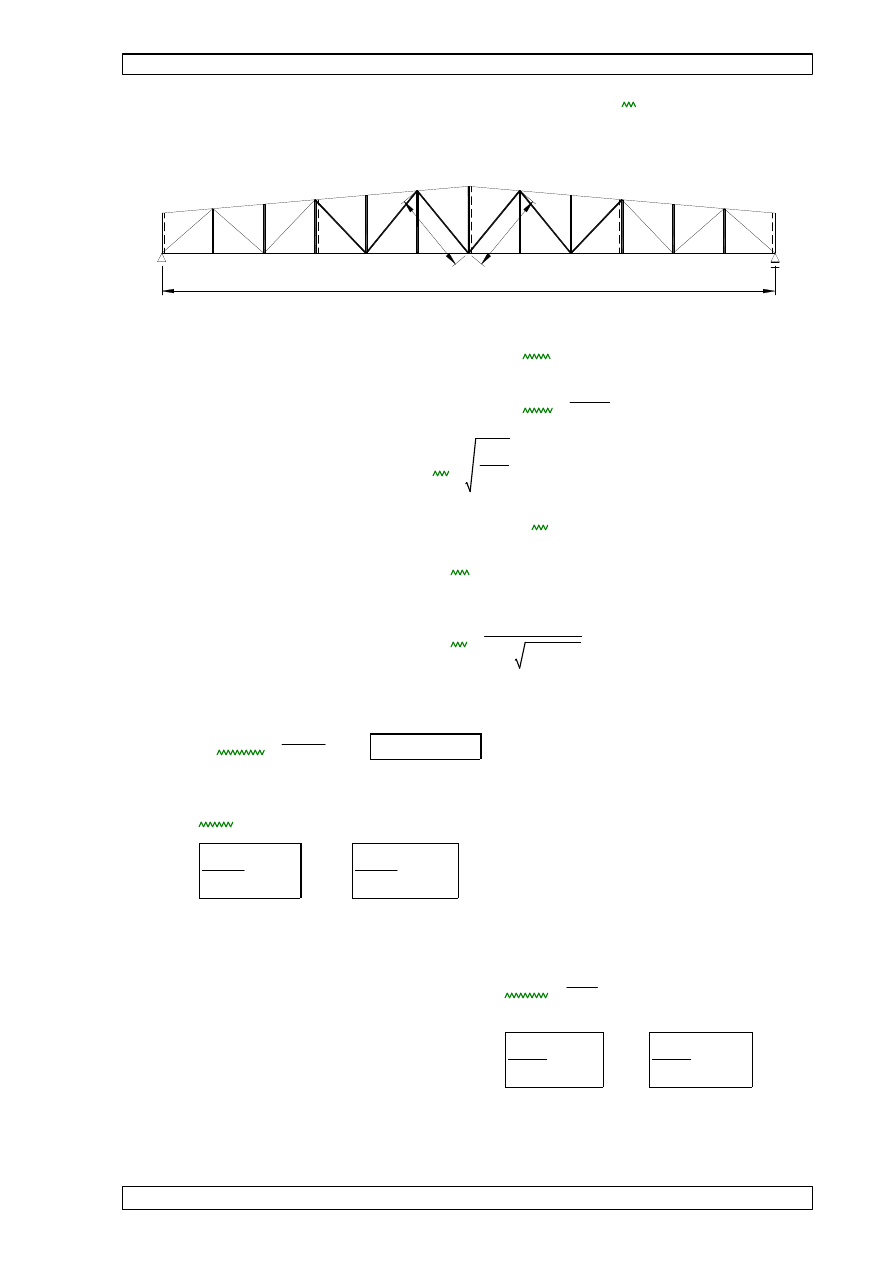
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

- dłudo

ść

teoretyczna pr

ę

ta mi

ę

dzy w

ę

złami:

lt

3.02m

:=

wyboczenie w płaszczy

ź

nie i z płaszczyzny kratownicy:

•

B=23000

3.0

2m

3.

02

m

- obliczeniowa długo

ść

wyboczeniowa:

Lcr

1.0lt

:=

Lcr 3020 mm

⋅

=

- siła krytyczna przy wyboczeniu:

Ncr

π

2

E I

⋅

Lcr

2

:=

Ncr 53.95 kN

⋅

=

- smukło

ść

wzgl

ę

dna y-y:

λ

A fy

⋅

Ncr

:=

λ

2.14

=

- parametr imperfekcji:

dla krzywej "c"

α

0.49

:=

- parametr krzywej wyboczenia:

Φ

0.5 1

α λ

0.2

−

(

)

⋅

+

λ

2

+





⋅

:=

- współczynnik wyboczeniowy:

χ

1

Φ

Φ

2

λ

2

−

+

:=

χ

0.17

=

no

ś

no

ść

elementu na wyboczenie:

•

Nb.Rd

χ

A

⋅

fy

⋅

γ

M1

:=

Nb.Rd 43.1 kN

⋅

=

warunek no

ś

no

ś

ci:

•

NEd

NEd.c

:=

NEd 35.76 kN

⋅

=

NEd

Nb.Rd

0.83

=

NEd

Nb.Rd

1

≤

1

=

- warunek spełniony

9.4.5 SPRAWDZENIE NO

Ś

NO

Ś

CI NA ROZCI

Ą

GANIE:

no

ś

no

ść

przekroju na rozci

ą

ganie:

•

Nt.Rd

A fy

⋅

γ

M0

:=

Nt.Rd 246.73 kN

⋅

=

warunek no

ś

no

ś

ci:

•

NEd.t

Nt.Rd

0.18

=

NEd.t

Nt.Rd

1

≤

1

=

Projektował: Artur Sta

ń

czewski

Strona 35

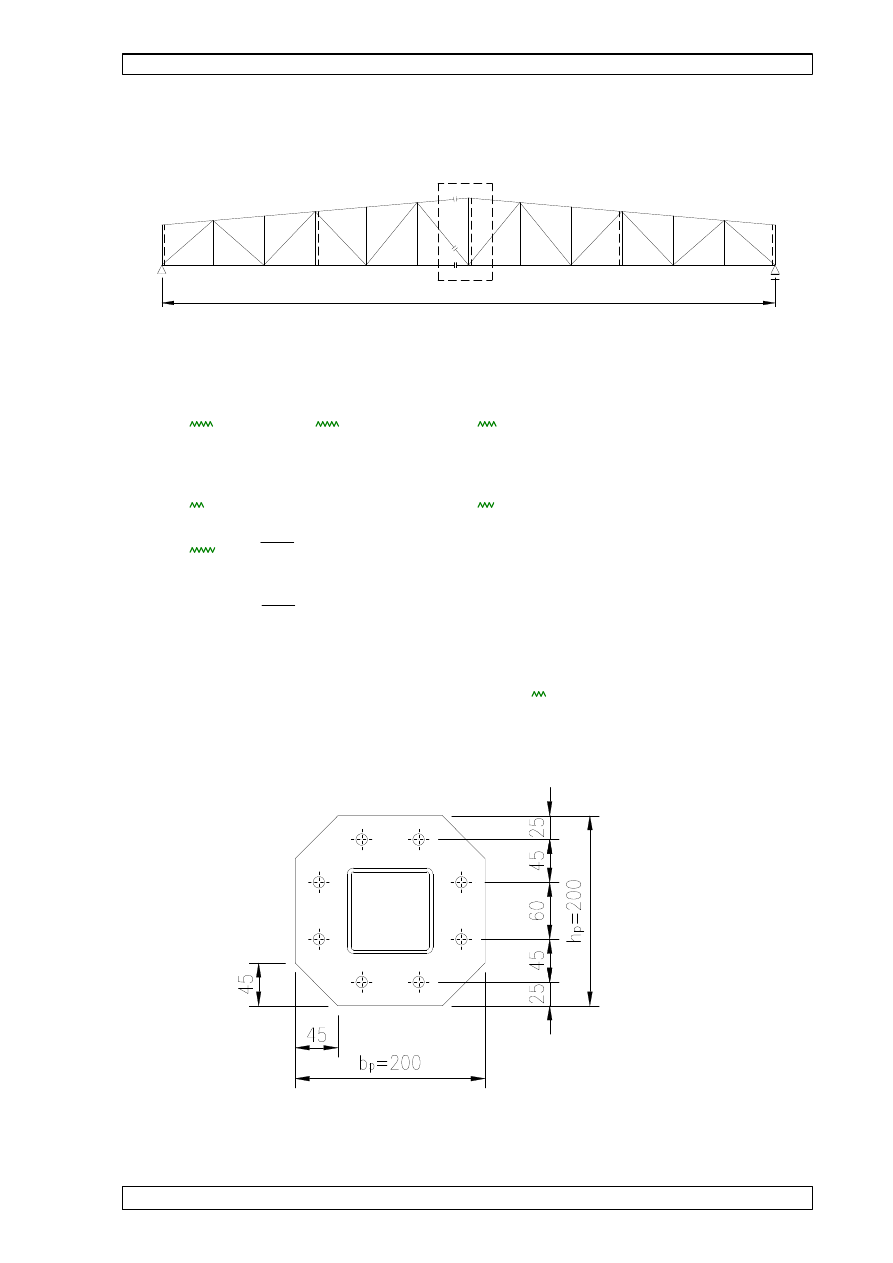
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

10. OBLICZENIE POŁ

Ą

CZENIA MONTA

ś

OWEGO KRATOWNICY.

Przyj

ę

to poł

ą

czenie doczołowe kategorii E (spr

ęż

ane)

B=23000

maksymalna siła rozci

ą

gajaca (pr

ę

ty 18, 19 - pas dolny)

•

FEd

370.62kN

:=

wymiary blachy czołowej:

•

hp

200mm

:=

bp

hp

:=

tp

28mm

:=

ś

ruby M12 klasy 8.8:

•

d

12mm

:=

d0

d

2mm

+

:=

A

π

0.5d

(

)

2

⋅

:=

As

84.3mm

2

:=

fyb

640

N

mm

2

:=

- granica plastyczno

ś

ci

ś

rub

fub

800

N

mm

2

:=

- wytrzymało

ść

na rozci

ą

ganie

rozstawy

ś

rub:

•

emin

1.2d0

:=

przyj

ę

to

e

25mm

:=

pmin

2.2d0

:=

przyj

ę

to

p

60mm

:=

e2

45mm

:=

Projektował: Artur Sta

ń

czewski

Strona 36

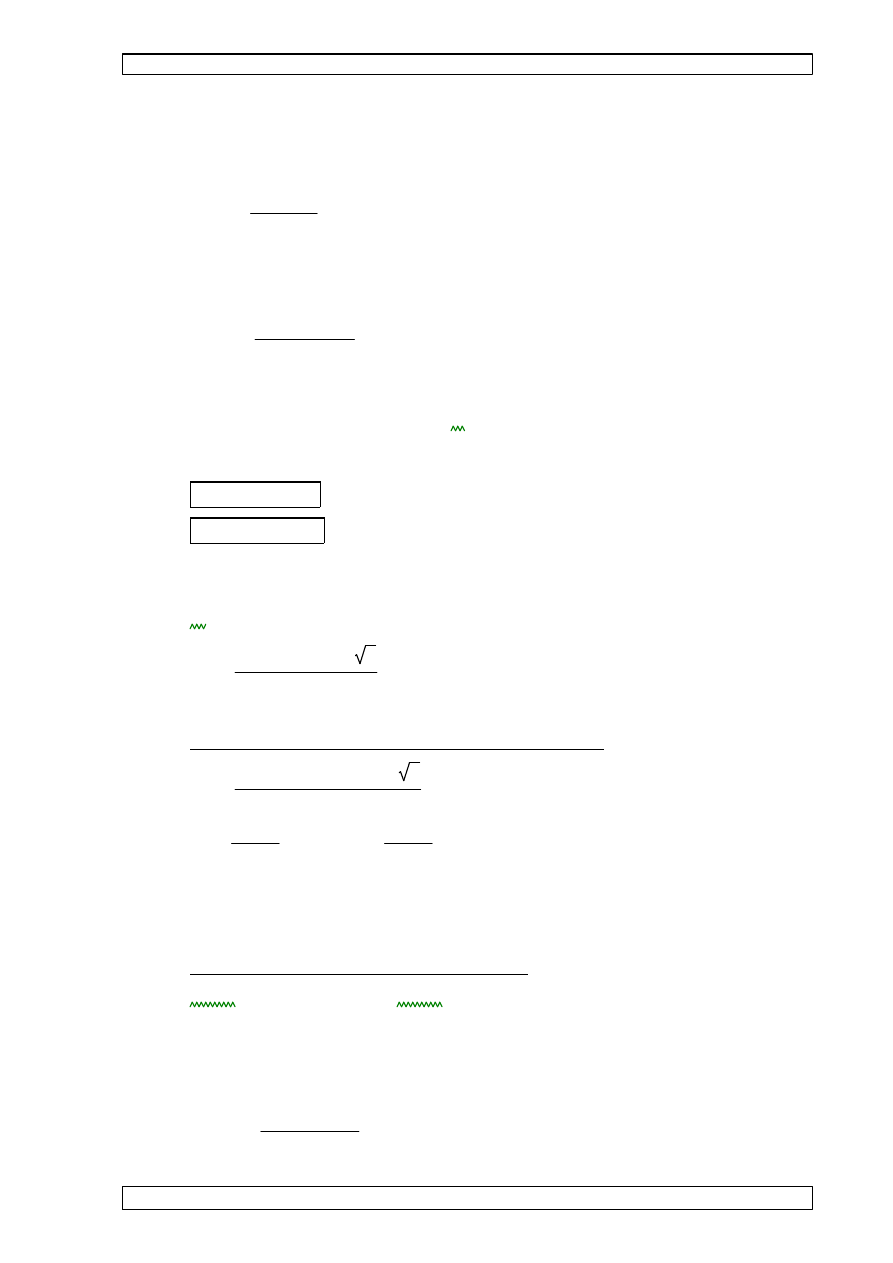
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

10.1 OBLICZENIE NO

Ś

NO

Ś

CI POŁ

Ą

CZENIA NA ROZCI

Ą

GANIE I PRZECI

Ą

GNIECIE ŁBA.

obliczenie no

ś

no

ś

ci na rozci

ą

ganie:

•

k2

0.9

:=

γ

M2

1.25

=

Ft.Rd

k2 fub

⋅

As

⋅

γ

M2

:=

Ft.Rd 48.56 kN

⋅

=

obliczenie no

ś

no

ś

ci ł

ą

czników ze wzgl

ę

du na przeci

ą

gniecie łba

ś

ruby:

•

dm

20.03mm

:=

Bp.Rd

0.6

π

⋅

dm

⋅

tp

⋅

fu

⋅

γ

M2

:=

Bp.Rd 431.32 kN

⋅

=

sprawdzenie warunków nosno

ś

ci:

•

- przyj

ę

to ilo

ść

ś

rub w poł

ą

czeniu:

n

8

:=

n Ft.Rd

⋅

388.45 kN

⋅

=

n Bp.Rd

⋅

3450.565 kN

⋅

=

FEd n Ft.Rd

⋅

≤

1

=

- warunek spełniony

FEd n Bp.Rd

⋅

≤

1

=

- warunek spełniony

10.2 OBLICZENIE NO

Ś

NO

Ś

CI BLACHY CZOŁOWEJ PRZY ZGINANIU.

w

hp 2e

−

:=

twb

2 tf

⋅

:=

a

3mm

:=

n1

e

:=

m1

w

twb

−

2 0.8

⋅

a

⋅

2

⋅

−

2

:=

m1 67.61 mm

⋅

=

Ft.Rd 48.56 kN

⋅

=

- obliczenie długo

ś

ci efektywnej dla pojedynczego szeregu

ś

rub:

m2

hp p

−

2 twb

⋅

−

2 0.8

⋅

a

⋅

2

⋅

−

2

:=

m2 58.61 mm

⋅

=

λ

1

m1

m1 e

+

:=

λ

2

m2

m1 e

+

:=

αλ

4.5

:=

leff.cp

2

π

⋅

m1

⋅

:=

leff.nc

αλ

m1

⋅

:=

leff.1

min leff.cp leff.nc

,

(

)

:=

- obliczenie długo

ś

ci efektywnej dla grupy szeregów:

leff.cp

π

m1

⋅

p

+

:=

leff.nc

0.5 p

⋅

αλ

m1

⋅

+

2 m1

⋅

0.625 e

⋅

−

(

)

−

:=

leff.2

min leff.cp leff.nc

,

(

)

:=

przyj

ę

to:

leff

min leff.1 leff.2

,

(

)

:=

Mpl.Rd

0.25 leff

⋅

tp

2

⋅

fy

⋅

γ

M0

:=

Mpl.Rd 14.93 kNm

⋅

=

Projektował: Artur Sta

ń

czewski

Strona 37

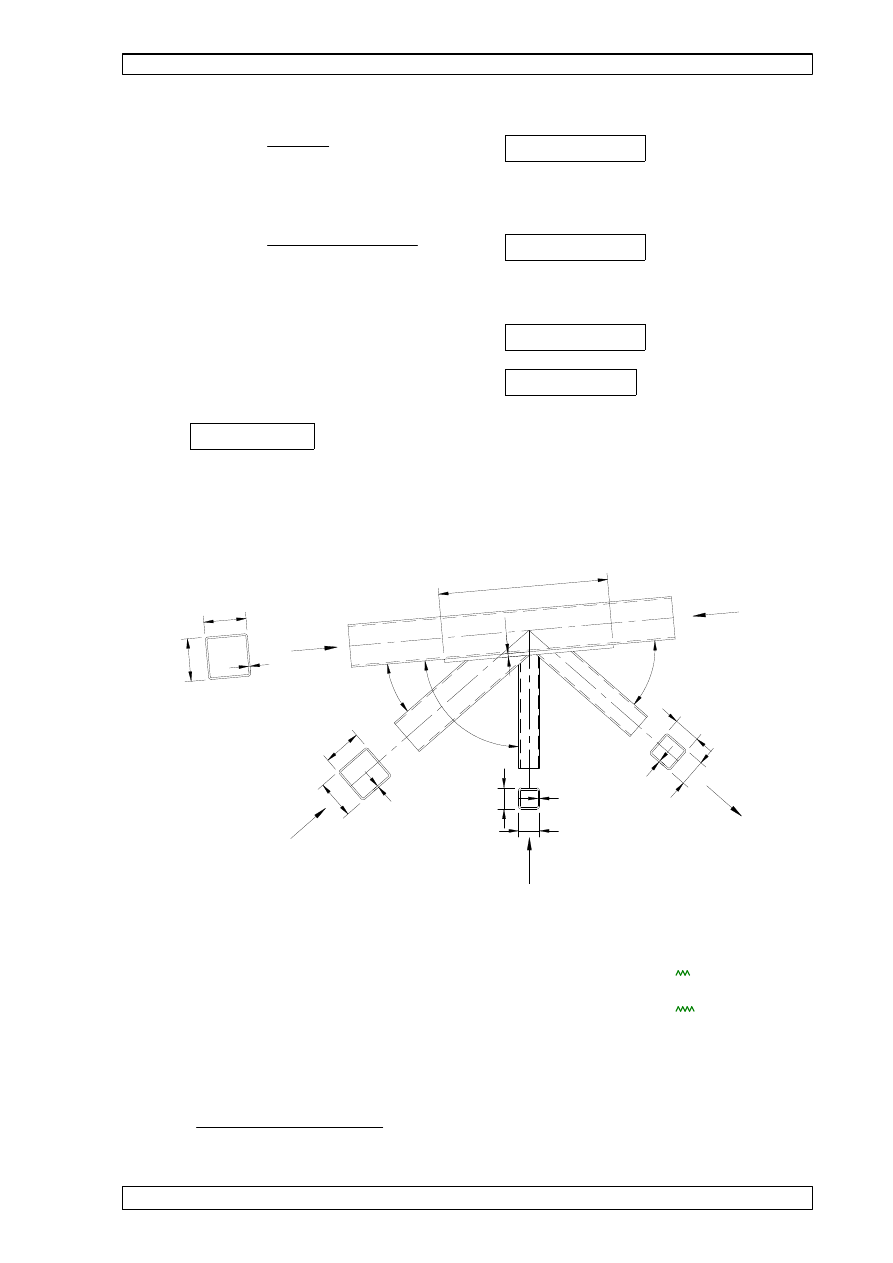
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

Model 1 zniszczenia: Całkowite uplastycznienie półki.

•

FT.1.Rd

4 Mpl.Rd

⋅

m1

:=

FT.1.Rd 883.63 kN

⋅

=

Model 2 zniszczenia: Zniszczenie

ś

rub wraz z uplastycznieniem półki.

•

FT.2.Rd

2 Mpl.Rd

⋅

n1 n

⋅

Ft.Rd

⋅

+

m1 n1

+

:=

FT.2.Rd 427.41 kN

⋅

=

Model 3 zniszczenia: Zniszczenie

ś

rub.

•

FT.3.Rd

n Ft.Rd

⋅

:=

FT.3.Rd 388.45 kN

⋅

=

Ft1.Rd

min FT.1.Rd FT.2.Rd

,

FT.3.Rd

,

(

)

:=

Ft1.Rd 388.45 kN

⋅

=

FEd Ft1.Rd

≤

1

=

- warunek spełniony

11. SPRAWDZENIE W

Ę

ZŁÓW KRATOWNICY.

11.1 SPRAWDZENIE W

Ę

ZŁA NR 2, 12.

N

1

N

2

b

1

b

2

t

1

h

2

b

2

t

2

h

3

b

3

t

3

N

3

h

0

b

0

t

0

t

p

N

0.Ed

N

p.Ed

l

p

?

1

?

3

?

2

geometria w

ę

zła:

•

b0

100mm

:=

h0

b0

:=

t0

4mm

:=

e0

25mm

:=

g

16mm

:=

b1

90mm

:=

h1

b1

:=

t1

4mm

:=

θ

1

36deg

:=

tp

8mm

:=

b2

63.5mm

:=

h2

b2

:=

t2

4mm

:=

θ

2

46deg

:=

γ

M5

1.0

:=

b3

50mm

:=

h3

b3

:=

t3

4mm

:=

θ

3

85deg

:=

β

b1 b2

+

b3

+

h1

+

h2

+

h3

+

6 b0

⋅

:=

β

0.68

=

Projektował: Artur Sta

ń

czewski

Strona 38

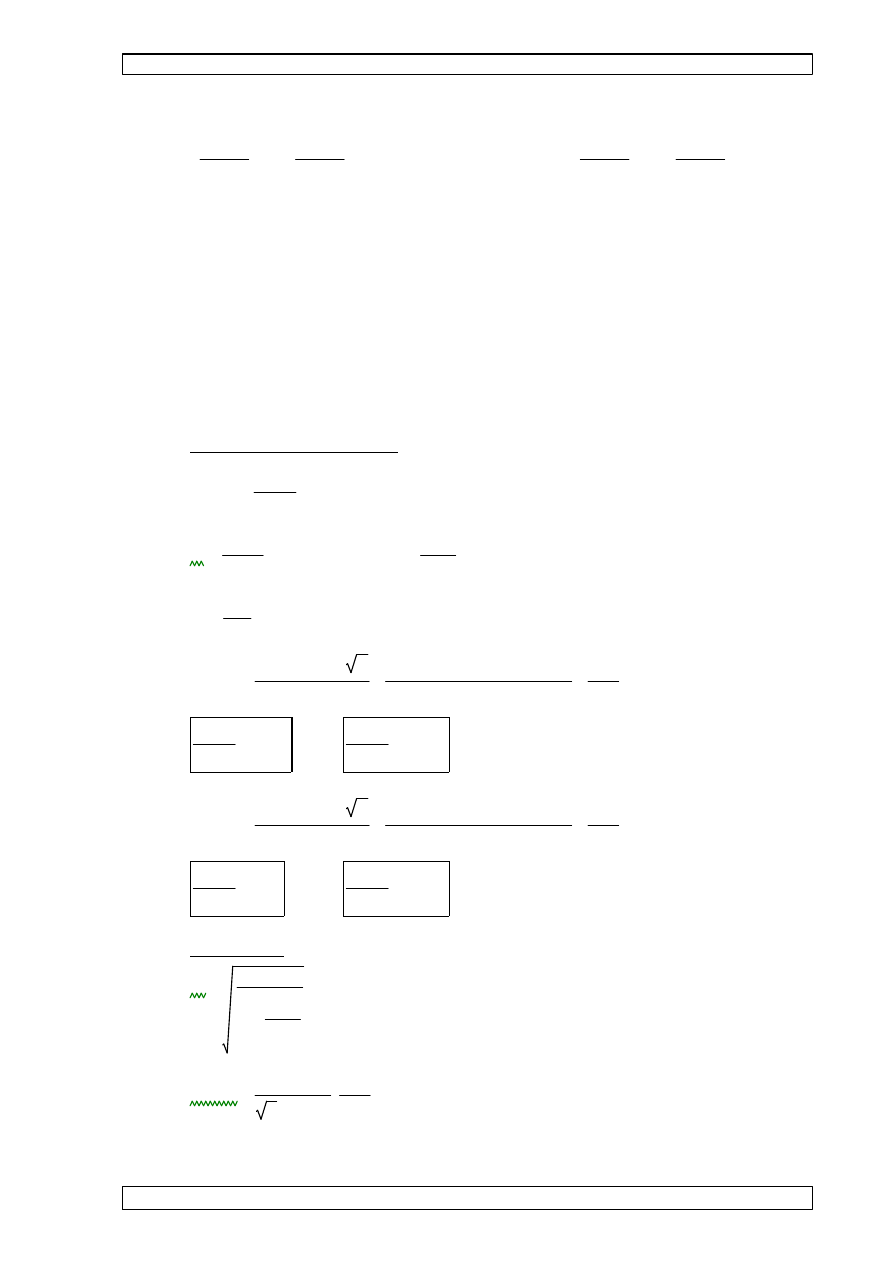
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

lpw

400mm

:=

bpw

100mm

:=

1.5

h1

sin

θ

1

( )

g

+

h2

sin

θ

2

( )

+









⋅

386.09 mm

⋅

=

lpw 1.5

h1

sin

θ

1

( )

g

+

h2

sin

θ

2

( )

+









⋅

≥

1

=

b0 2.t0

−

92 mm

⋅

=

bp b0 2.t0

−

≥

1

=

2 t1

⋅

8 mm

⋅

=

tp 2 t1

⋅

≥

1

=

obci

ąż

enie w

ę

zła (kombinacja SGN/195):

•

Np.Ed

0kN

:=

N0.Ed

270.18kN

:=

N1.Ed

215.76kN

:=

N2.Ed

140.94kN

:=

N3.Ed

0.24kN

:=

obliczenie no

ś

no

ś

ci w

ę

zła:

•

- zniszczenie przystykowe pasa:

A0

14.95cm

2

:=

Wel.0

45.27cm

3

:=

σ

0.Ed

N0.Ed

A0

:=

σ

0.Ed

180.72 MPa

⋅

=

n

σ

0.Ed

fy

:=

kn

1.3

0.4 n

⋅

β

−

:=

kn 1

=

γ

b0

2 tp

⋅

:=

N1.Rd

8.9 kn

⋅

fy

⋅

tp

2

⋅

γ

⋅

sin

θ

1

( )

b1 b2

+

b3

+

h1

+

h2

+

h3

+

6 b0

⋅









⋅

1

γ

M5

⋅

:=

N1.Rd 583.28 kN

⋅

=

N1.Ed

N1.Rd

0.37

=

N1.Ed

N1.Rd

1

≤

1

=

N2.Rd

8.9 kn

⋅

fy

⋅

tp

2

⋅

γ

⋅

sin

θ

2

( )

b1 b2

+

b3

+

h1

+

h2

+

h3

+

6 b0

⋅









⋅

1

γ

M5

⋅

:=

N2.Rd 476.61 kN

⋅

=

N2.Ed

N2.Rd

0.3

=

N2.Ed

N2.Rd

1

≤

1

=

-

ś

ci

ę

cie pasa:

α

1

1

4 g

2

⋅

3 tp

2

⋅

+

:=

Av

2 h0

⋅

α

b0

⋅

+

(

)

tp

⋅

:=

N1.Rd

fy Av

⋅

3 sin

θ

1

( )

⋅

1

γ

M5

⋅

:=

N1.Rd 668.76 kN

⋅

=

Projektował: Artur Sta

ń

czewski

Strona 39

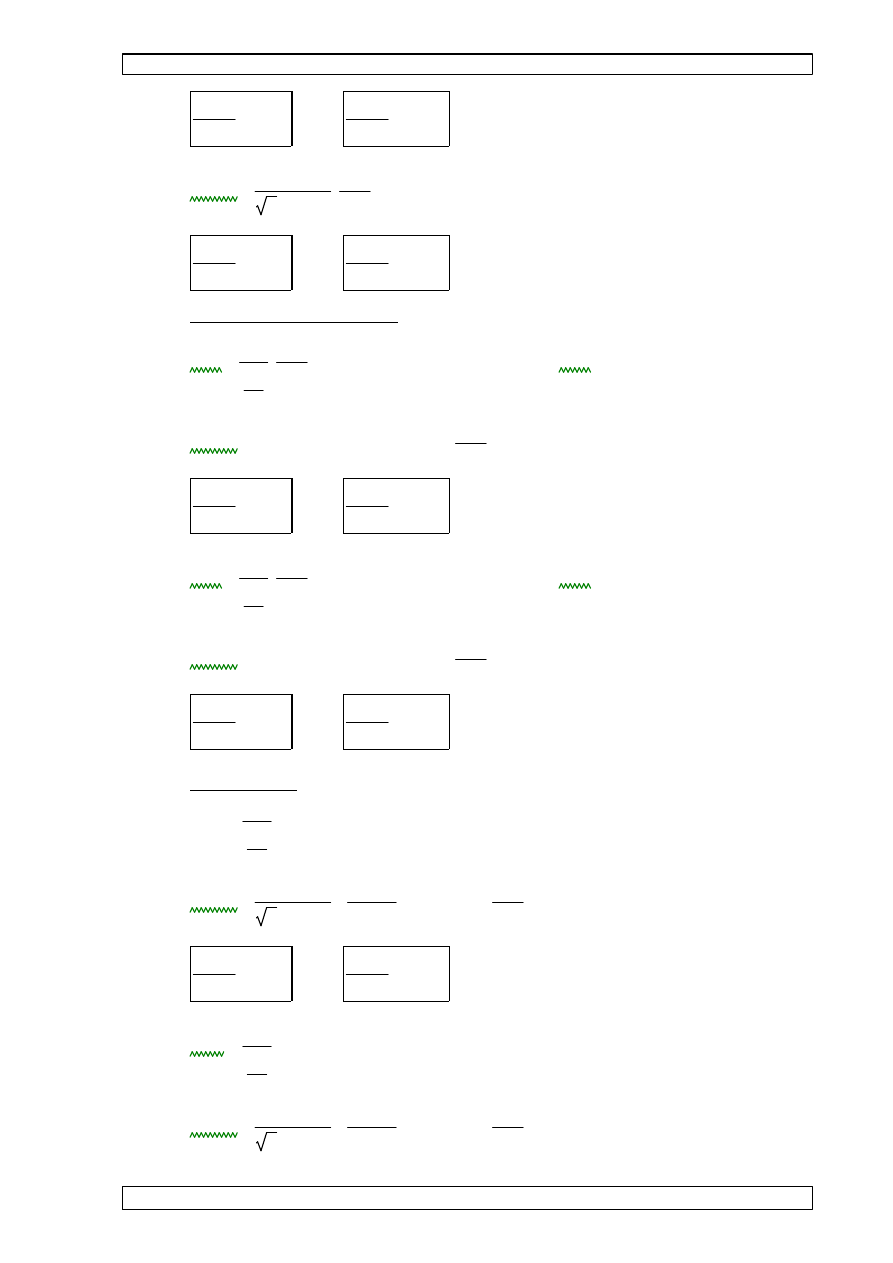
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

N1.Ed

N1.Rd

0.32

=

N1.Ed

N1.Rd

1

≤

1

=

N2.Rd

fy Av

⋅

3 sin

θ

2

( )

⋅

1

γ

M5

⋅

:=

N2.Rd 546.46 kN

⋅

=

N2.Ed

N2.Rd

0.26

=

N2.Ed

N2.Rd

1

≤

1

=

- zniszczenie pr

ę

ta skratowania:

beff

10

b0

tp

fy tp

⋅

fy t1

⋅

⋅

b1

⋅

:=

beff b1

≤

0

=

beff

b1

:=

N1.Rd

fy t1

⋅

2 h1

⋅

4 t1

⋅

−

b1

+

beff

+

(

)

⋅

1

γ

M5

⋅

:=

N1.Rd 488.48 kN

⋅

=

N1.Ed

N1.Rd

0.44

=

N1.Ed

N1.Rd

1

≤

1

=

beff

10

b0

tp

fy tp

⋅

fy t2

⋅

⋅

b2

⋅

:=

beff b2

≤

0

=

beff

b2

:=

N2.Rd

fy t2

⋅

2 h2

⋅

4 t2

⋅

−

b2

+

beff

+

(

)

⋅

1

γ

M5

⋅

:=

N2.Rd 337.96 kN

⋅

=

N2.Ed

N2.Rd

0.42

=

N2.Ed

N2.Rd

1

≤

1

=

- przebicie pasa:

be.p

10

b0

tp

b1

⋅

:=

be.p b1

≤

1

=

N1.Rd

fy tp

⋅

3 sin

θ

1

( )

⋅

2 h1

⋅

sin

θ

1

( )

b1

+

be.p

+









⋅

1

γ

M5

⋅

:=

N1.Rd 1306.18 kN

⋅

=

N1.Ed

N1.Rd

0.17

=

N1.Ed

N1.Rd

1

≤

1

=

be.p

10

b0

tp

b2

⋅

:=

be.p b2

≤

1

=

N2.Rd

fy tp

⋅

3 sin

θ

2

( )

⋅

2 h1

⋅

sin

θ

2

( )

b2

+

be.p

+









⋅

1

γ

M5

⋅

:=

N1.Rd 1306.18 kN

⋅

=

Projektował: Artur Sta

ń

czewski

Strona 40

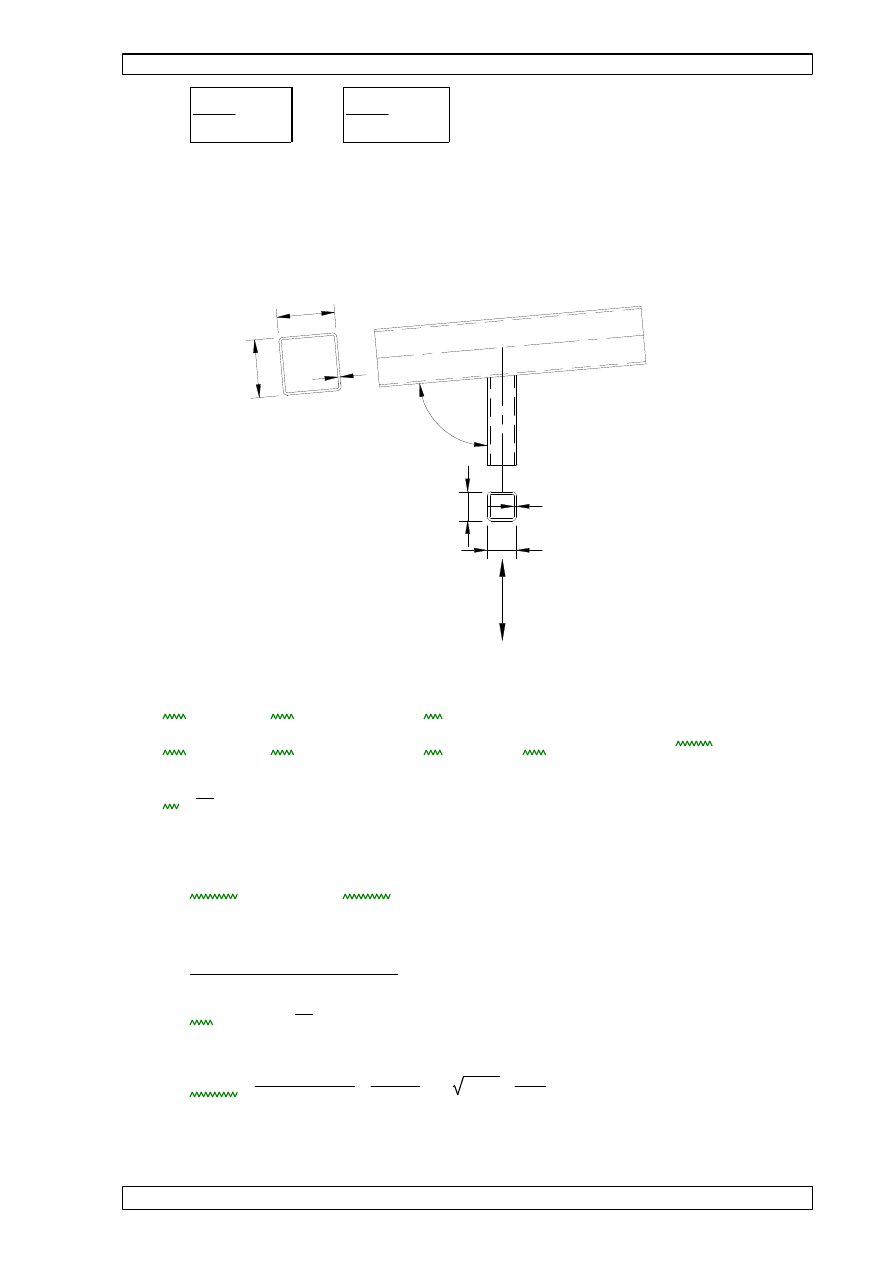
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

N2.Ed

N2.Rd

0.17

=

N2.Ed

N2.Rd

1

≤

1

=

N1.Ed sin

θ

1

( )

⋅

N3.Ed sin

θ

3

( )

⋅

+

N1.Rd sin

θ

1

( )

⋅

≤

1

=

N2.Ed sin

θ

2

( )

⋅

N1.Rd sin

θ

1

( )

⋅

≤

1

=

11.2 SPRAWDZENIE W

Ę

ZŁA NR 7.

h

1

b

1

t

1

N

1

h

0

b

0

t

0

?

1

geometria w

ę

zła:

•

b0

100mm

:=

h0

b0

:=

t0

4mm

:=

γ

M5

1.0

:=

b1

50mm

:=

h1

b1

:=

t1

4mm

:=

θ

1

85deg

:=

β

b1

b0

:=

β

0.5

=

obci

ąż

enie w

ę

zła (kombinacja SGN/195):

•

N1.Ed

35.97kN

:=

N0.Ed

357.43kN

:=

obliczenie no

ś

no

ś

ci w

ę

zła:

•

- zniszczenie przystykowe pasa:

kn

1

:=

η

h1

b0

:=

N1.Rd

kn fy

⋅

t0

2

⋅

1

β

−

(

) sin

θ

1

( )

⋅

2

η

⋅

sin

θ

1

( )

4

1

β

−

⋅

+













⋅

1

γ

M5

⋅

:=

N1.Rd 43.7 kN

⋅

=

Projektował: Artur Sta

ń

czewski

Strona 41

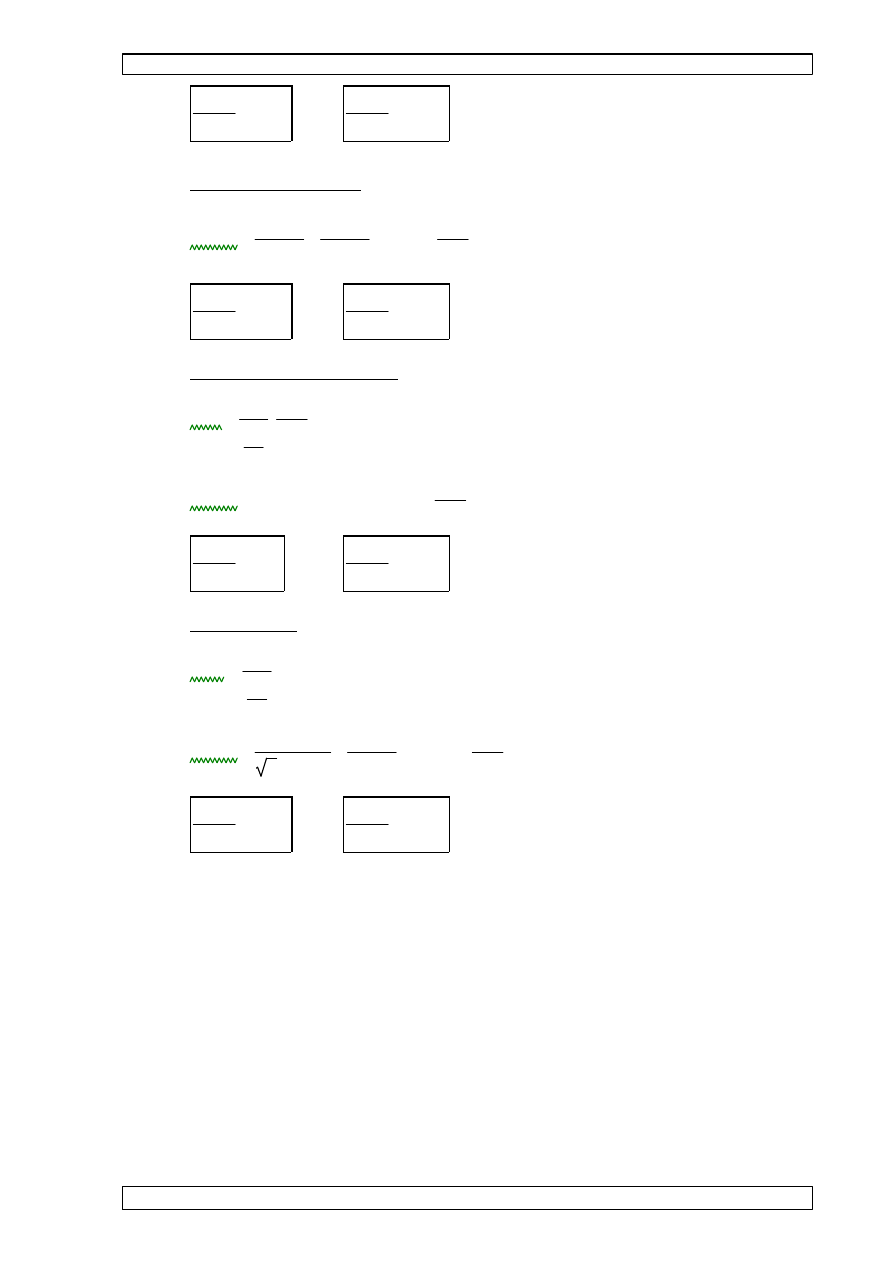
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

N1.Ed

N1.Rd

0.82

=

N1.Ed

N1.Rd

1

≤

1

=

- wyboczenie boków pasa:

N1.Rd

fy t0

⋅

sin

θ

1

( )

2 h1

⋅

sin

θ

1

( )

10 t0

⋅

+









⋅

1

γ

M5

⋅

:=

N1.Rd 200.1 kN

⋅

=

N1.Ed

N1.Rd

0.18

=

N1.Ed

N1.Rd

1

≤

1

=

- zniszczenie pr

ę

ta skratowania:

beff

10

b0

t0

fy t0

⋅

fy t1

⋅

⋅

b1

⋅

:=

beff b1

≤

1

=

N1.Rd

fy t1

⋅

2 h1

⋅

4 t1

⋅

−

2 beff

⋅

+

(

)

⋅

1

γ

M5

⋅

:=

N1.Rd 176.08 kN

⋅

=

N1.Ed

N1.Rd

0.2

=

N1.Ed

N1.Rd

1

≤

1

=

- przebicie pasa:

be.p

10

b0

t0

b1

⋅

:=

be.p b1

≤

1

=

N1.Rd

fy tp

⋅

3 sin

θ

1

( )

⋅

2 h1

⋅

sin

θ

1

( )

2 be.p

⋅

+









⋅

1

γ

M5

⋅

:=

N1.Rd 231.06 kN

⋅

=

N1.Ed

N1.Rd

0.16

=

N1.Ed

N1.Rd

1

≤

1

=

Projektował: Artur Sta

ń

czewski

Strona 42

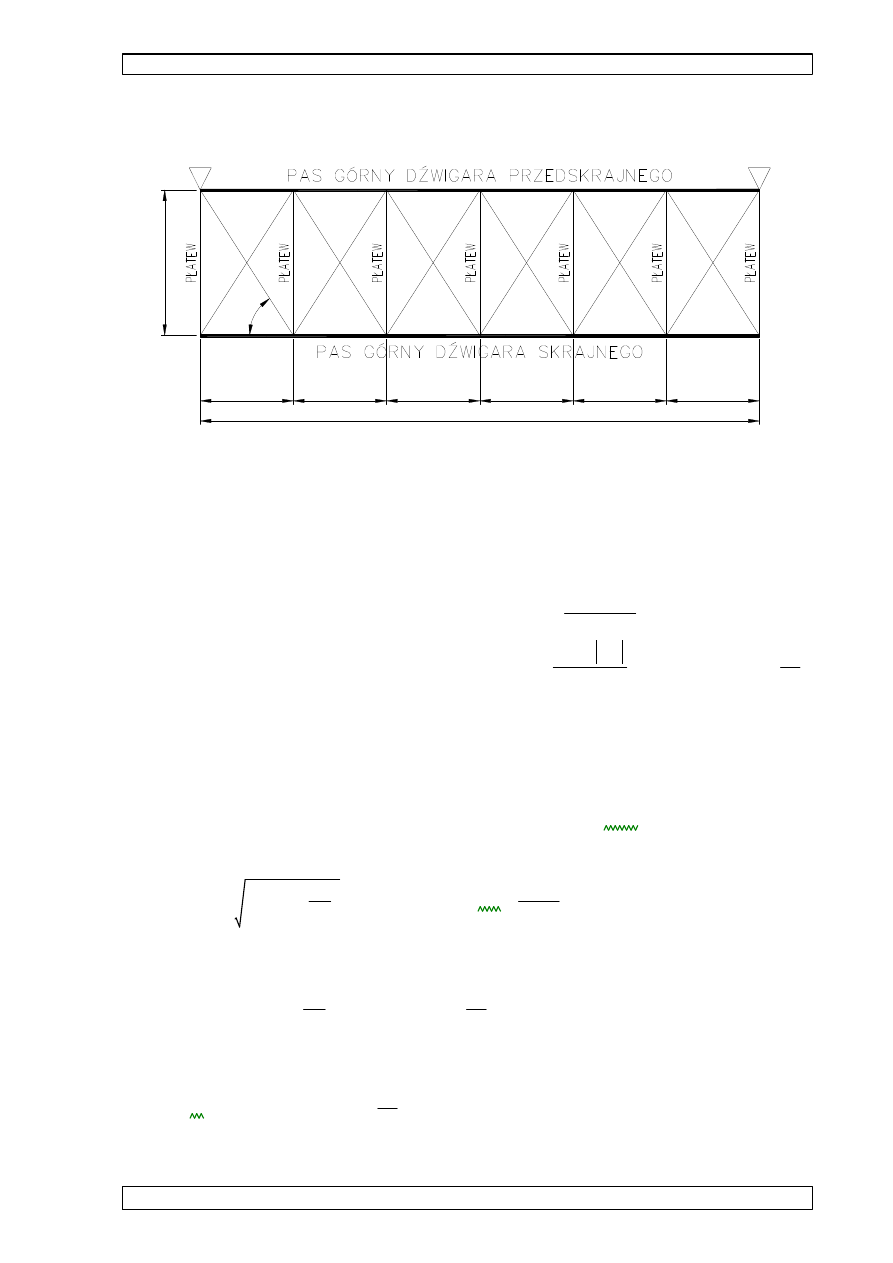
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

12. OBLICZENIA ST

Ęś

ENIA POŁACIOWEGO DACHU.

12.1 SCHEMAT T

Ęś

NIKA

6

m

3.844m

3.844m

3.855m

3.855m

3.844m

3.844m

23.087m

5

7

°

12.2 OBCI

Ąś

ENIE ST

Ęś

ENIA POŁACIOWEGO.

12.2.1 OBCI

Ąś

ENIE T

Ęś

NIKA OD WIATRU.

obci

ąż

enie wiatrem

ś

ciany szczytowej (parcie):

•

wD 0.66 kPa

⋅

=

obci

ąż

enie wiatrem

ś

ciany szczytowej (ssanie):

•

wE

0.37

−

kPa

⋅

=

ś

rednia wysoko

ść

d

ź

wigara:

•

hws

hwo hwk

+

2

:=

obci

ąż

enie ci

ą

głe t

ęż

nika od wiatru:

•

wt

wD

wE

+

2

γ

ws

⋅

hws

⋅

:=

wt 1.75

kN

m

⋅

=

12.2.2 OBCI

Ąś

ENIE T

Ęś

NIKA OD IMPREFEKCJI D

Ź

WIGARÓW.

liczba st

ęż

anych d

ź

wigarów:

•

md

4

:=

rozpi

ę

to

ść

t

ęż

nika:

•

Lt

12 ap

⋅

10mm

+

:=

Lt 30.76m

=

maksymalna siła

ś

ciskaj

ą

ca w pasie górnym kratownicy:

•

NEd

375kN

:=

strzałka wst

ę

pnej imperfekcji łukowej:

•

α

m

0.5 1

1

md

+













⋅

:=

e0

α

m Lt

⋅

500

:=

e0 48.63 mm

⋅

=

obci

ąż

enie t

ęż

nika równowa

ż

ne oddziaływaniu imperfekcji d

ź

wigarów:

•

qd

md NEd

⋅

8

⋅

e0

Lt

2

⋅

:=

qd 0.62

kN

m

⋅

=

obci

ąż

enie całkowite od wiatru i imperfekcji:

•

p

wt qd

+

:=

p

2.36

kN

m

⋅

=

Projektował: Artur Sta

ń

czewski

Strona 43

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

ugi

ę

cie t

ęż

nika pod całkowitym obci

ąż

eniem:

•

- przybli

ż

ony moment bezwładno

ś

ci t

ęż

nika:

Apg

14.95cm

2

:=

Ite

0.9 aw

2

⋅

Apg

2

⋅

:=

Ite 2421900 cm

4

⋅

=

δ

p

5

384

p Lt

4

⋅

E Ite

⋅

⋅

:=

δ

p

5.41 mm

⋅

=

obci

ąż

enie i ugi

ę

cie t

ęż

nika z uwzgl

ę

dnieniem podatno

ś

ci:

•

- przybli

ż

enie 1:

qd1

md NEd

⋅

8

⋅

e0

δ

p

+

Lt

2

⋅

:=

qd1 0.686

kN

m

⋅

=

δ

q1

δ

p

qd1

p

⋅

:=

- przybli

ż

enie 2:

qd2

md NEd

⋅

8

⋅

e0

δ

q1

+

Lt

2

⋅

:=

qd2 0.637

kN

m

⋅

=

qd1 qd2

−

qd1

2%

≤

0

=

δ

q2

δ

p

qd2

p

⋅

:=

- przybli

ż

enie 3:

qd3

md NEd

⋅

8

⋅

e0

δ

q2

+

Lt

2

⋅

:=

qd3 0.635

kN

m

⋅

=

δ

q3

δ

p

qd3

p

⋅

:=

qd2 qd3

−

qd2

2%

≤

1

=

- ko

ń

czymy iteracje

przyjmujemy

q

max qd1 qd2

,

qd3

,

(

)

:=

q

0.686

kN

m

⋅

=

12.2 SPRAWDZENIE OBCI

Ąś

ENIA T

Ęś

NIKA W KALENICY.

maksymalna siła skupiona obci

ąż

ajaca t

ęż

nik:

•

F

α

m NEd

⋅

100

:=

F

2.965 kN

⋅

=

porównanie momentów obci

ąż

aj

ą

cych t

ęż

nik:

•

Mqd

0.125qd Lt

2

⋅

:=

Mqd 72.95 kNm

⋅

=

- moment od imperfekcji

MF

0.25F Lt

⋅

:=

MF 22.8 kNm

⋅

=

- moment od siły skupionej

porównanie sił

ś

ciskaj

ą

cych w płatwi:

•

Nqd

ap q

⋅

:=

Nqd 1.76 kN

⋅

=

- siła od imperfekcji

NF

F

:=

NF 2.965 kN

⋅

=

- moment od siły skupionej

Projektował: Artur Sta

ń

czewski

Strona 44

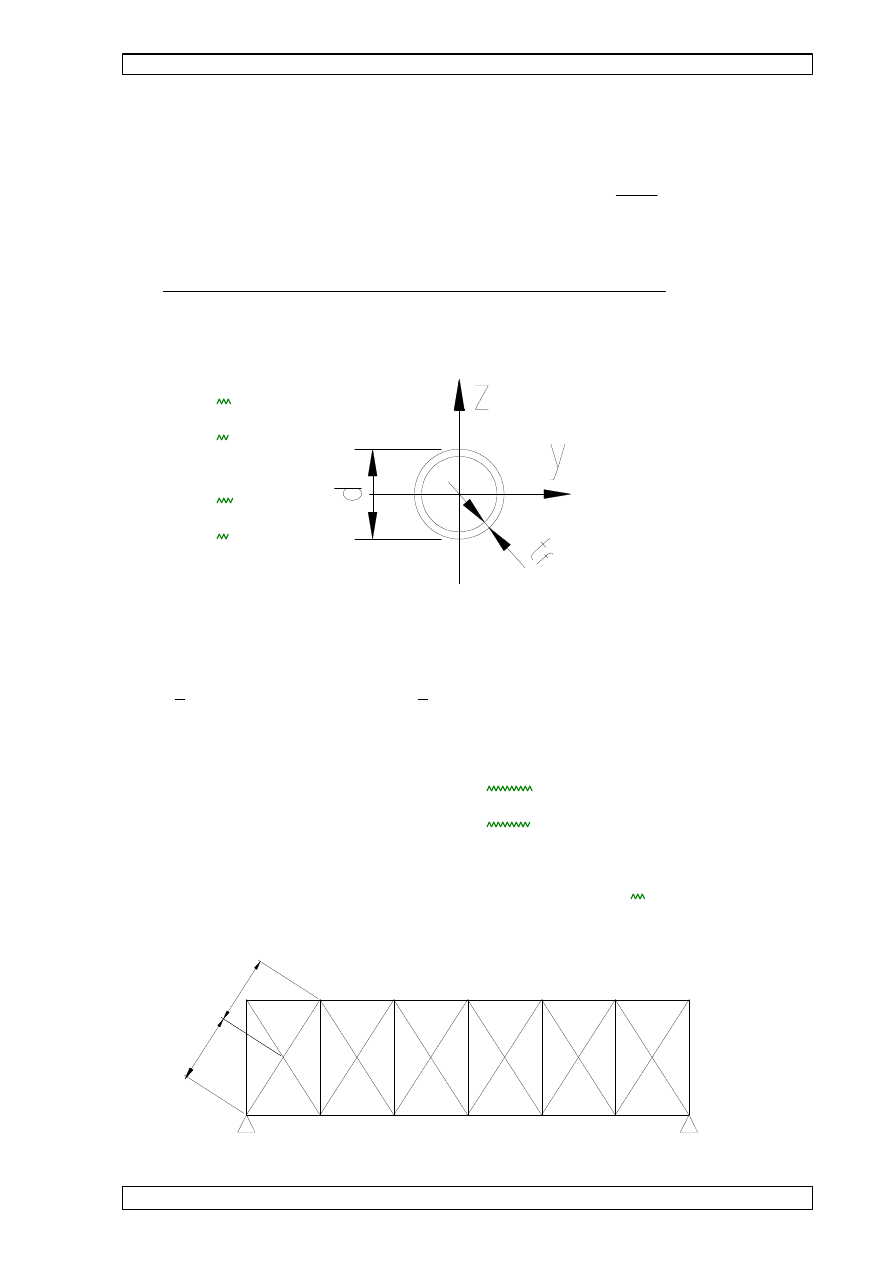
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

12.3 OBLICZENIA T

Ęś

NIKA POŁACIOWEGO.

Przyj

ę

to schemat statyczny kratownicy wolnopodpartej jak w pkt. 12.1

obci

ąż

enie w

ę

złów t

ęż

nika od imperfekcji i wiatru.

•

Pim.w

q 2

⋅

ap wt 2

⋅

ap

+

:=

Pim.w 12.46 kN

⋅

=

Pim.w

2

6.23 kN

⋅

=

12.4 WYNIKI OBLICZE

Ń

STATYCZNYCH.

SZCZEGÓŁOWE WYNIKI OBLICZE

Ń

ZAMIESZCZONO W ZAŁ

Ą

CZNIKU B.

12.5 WYMIAROWANIE PR

Ę

TÓW SKRATOWANIA.

12.5.1 CHARAKTERYSTYKI PRZEKROJU R 88.9x3:

d

88.9mm

:=

t

3mm

:=

A

8.10cm

2

:=

I

74.76cm

4

:=

12.5.2 SPRAWDZENIE KLASY PRZEKROJU:

ε

0.81

=

d

t

29.63

=

50

ε

2

33.1

=

d

t

50

ε

2

≤

1

=

- klasa 1

12.5.3 EKSTREMALNE SIŁY W PR

Ę

TACH:

maksymalna siła

ś

ciskaj

ą

ca:

•

NEd.c

19.58kN

:=

maksymalna siła rozci

ą

gaj

ą

ca:

•

NEd.t

10.83kN

:=

12.5.4 SPRAWDZENIE NO

Ś

NO

Ś

CI NA WYBOCZENIE:

- dłudo

ść

teoretyczna pr

ę

ta mi

ę

dzy w

ę

złami:

lt

3.56m

:=

wyboczenie w płaszczy

ź

nie i z płaszczyzny dachu:

•

3

.5

6

m

3

.5

6

m

Projektował: Artur Sta

ń

czewski

Strona 45

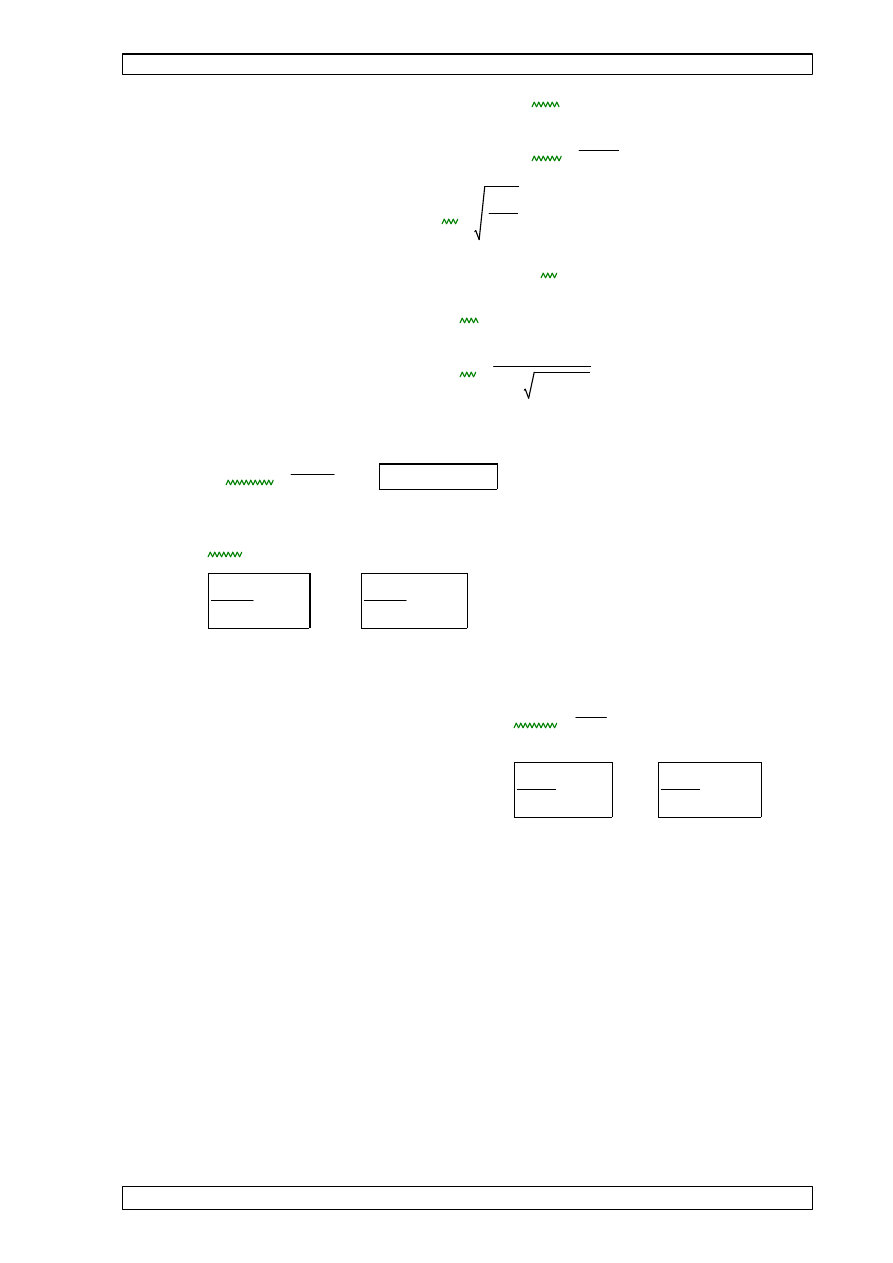
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

- obliczeniowa długo

ść

wyboczeniowa:

Lcr

2 lt

⋅

:=

Lcr 7.12 m

=

- siła krytyczna przy wyboczeniu:

Ncr

π

2

E I

⋅

Lcr

2

:=

Ncr 30.57 kN

⋅

=

- smukło

ść

wzgl

ę

dna y-y:

λ

A fy

⋅

Ncr

:=

λ

3.07

=

- parametr imperfekcji:

dla krzywej "c"

α

0.49

:=

- parametr krzywej wyboczenia:

Φ

0.5 1

α λ

0.2

−

(

)

⋅

+

λ

2

+





⋅

:=

- współczynnik wyboczeniowy:

χ

1

Φ

Φ

2

λ

2

−

+

:=

χ

0.09

=

no

ś

no

ść

elementu na wyboczenie:

•

Nb.Rd

χ

A

⋅

fy

⋅

γ

M1

:=

Nb.Rd 26.25 kN

⋅

=

warunek no

ś

no

ś

ci:

•

NEd

NEd.c

:=

NEd 19.58 kN

⋅

=

NEd

Nb.Rd

0.75

=

NEd

Nb.Rd

1

≤

1

=

- warunek spełniony

12.5.5 SPRAWDZENIE NO

Ś

NO

Ś

CI NA ROZCI

Ą

GANIE:

no

ś

no

ść

przekroju na rozci

ą

ganie:

•

Nt.Rd

A fy

⋅

γ

M0

:=

Nt.Rd 287.55 kN

⋅

=

warunek no

ś

no

ś

ci:

•

NEd.t

Nt.Rd

0.04

=

NEd.t

Nt.Rd

1

≤

1

=

Projektował: Artur Sta

ń

czewski

Strona 46

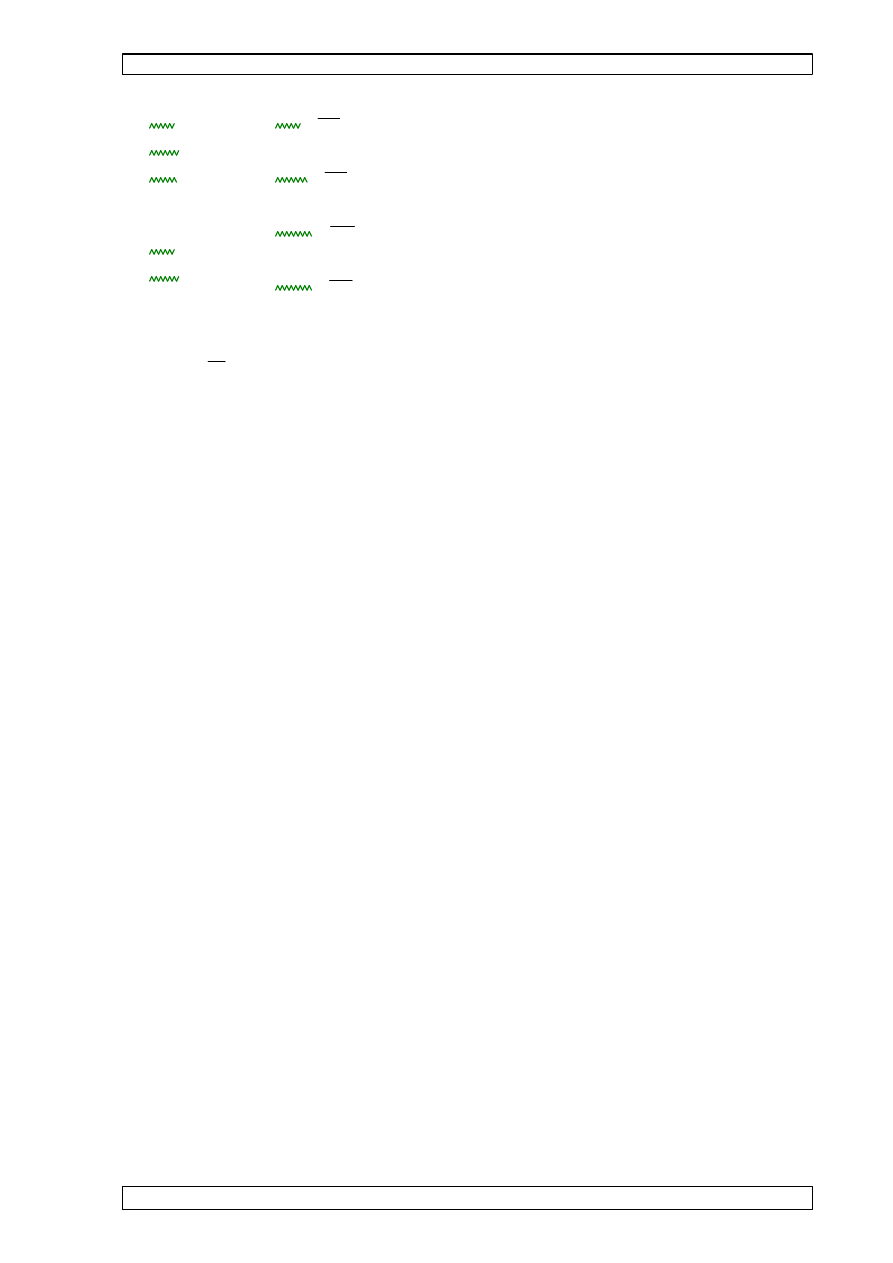
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

kN

1000N

:=

Pa

N

m

2

:=

MN

1000kN

:=

GN

1000MN

:=

kPa

kN

m

2

:=

m

1 m

=

MPa

MN

m

2

:=

cm

0.01m

:=

mm

0.001m

:=

GPa

GN

m

2

:=

s

1 s

=

g

9.81

m

s

2

=

kNm

kN m

⋅

:=

Erokod 3 Cz

ęść

1.1 Regóły ogólne i regóły dla budynków zał

ą

czmik krajowy EN 1993-1-1

Eurokod 1 Cz

ęść

1-1 Oddziływania ogólne..... zał. A2

Projektował: Artur Sta

ń

czewski

Strona 47

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

Ci

ęż

ar blachy z tablic Prószy

ń

ski i sp - ka

mp

10.56

kg

m

:=

mpp

mp g

⋅

:=

Eurokod 1 Cz

ęść

1-1 tabela 6.10

Projektował: Artur Sta

ń

czewski

Strona 48

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

Projektował: Artur Sta

ń

czewski

Strona 49

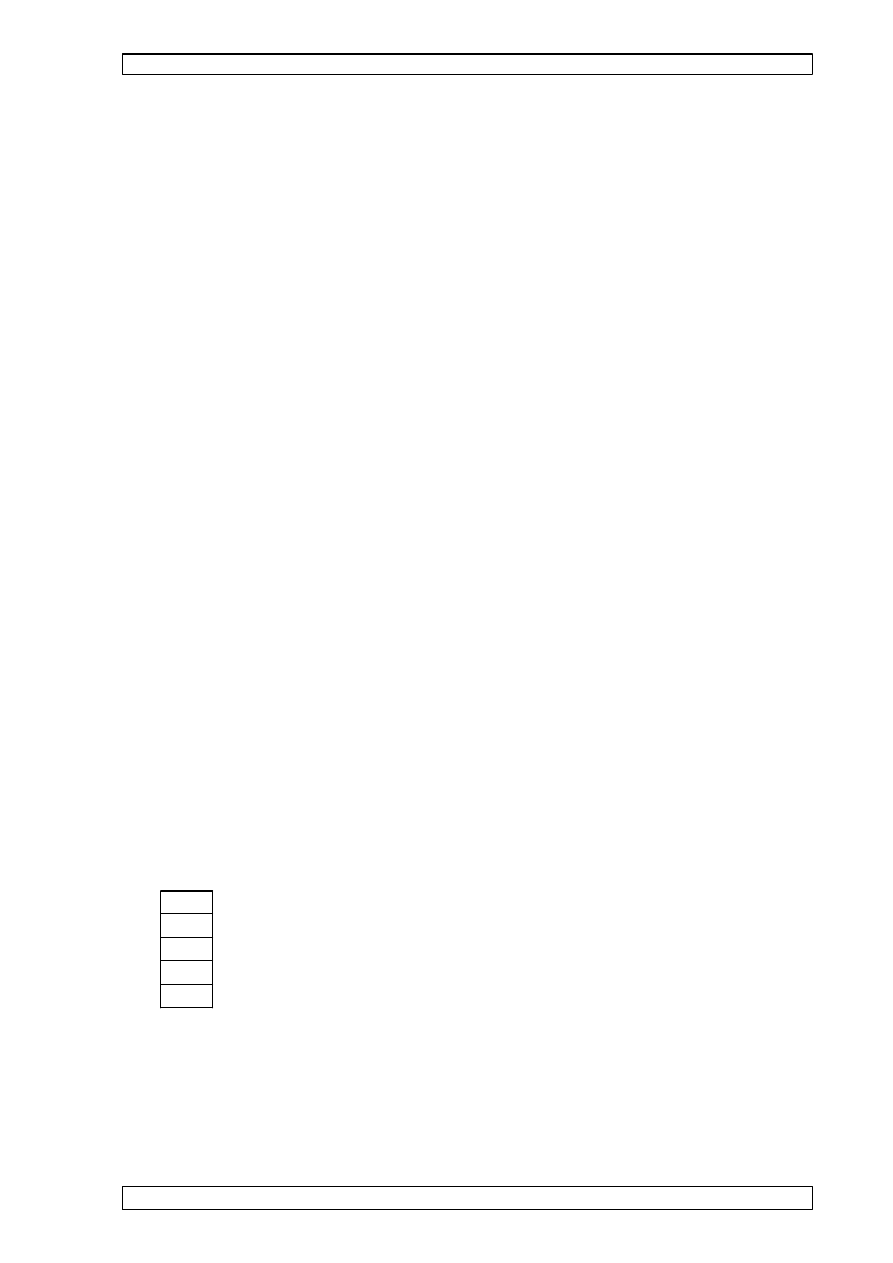
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

tz

i

2.96

2.96

2.96

2.96

2.96

mm

⋅

=

dA

i

=

Projektował: Artur Sta

ń

czewski

Strona 50

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

0.55

1.69

8.79

1.69

0.55

cm

2

⋅

Projektował: Artur Sta

ń

czewski

Strona 51

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

ω

0

i

-10.54

0

0

-169.29

-10.54

cm

2

⋅

=

ω

i

-10.54

-10.54

-10.54

-179.83

-190.38

cm

2

⋅

=

Projektował: Artur Sta

ń

czewski

Strona 52

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

Projektował: Artur Sta

ń

czewski

Strona 53

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

ygc 11.96 mm

⋅

=

zgc 148.5 mm

⋅

=

ysd 9.8 mm

⋅

=

zsd 142.4 mm

⋅

=

Projektował: Artur Sta

ń

czewski

Strona 54

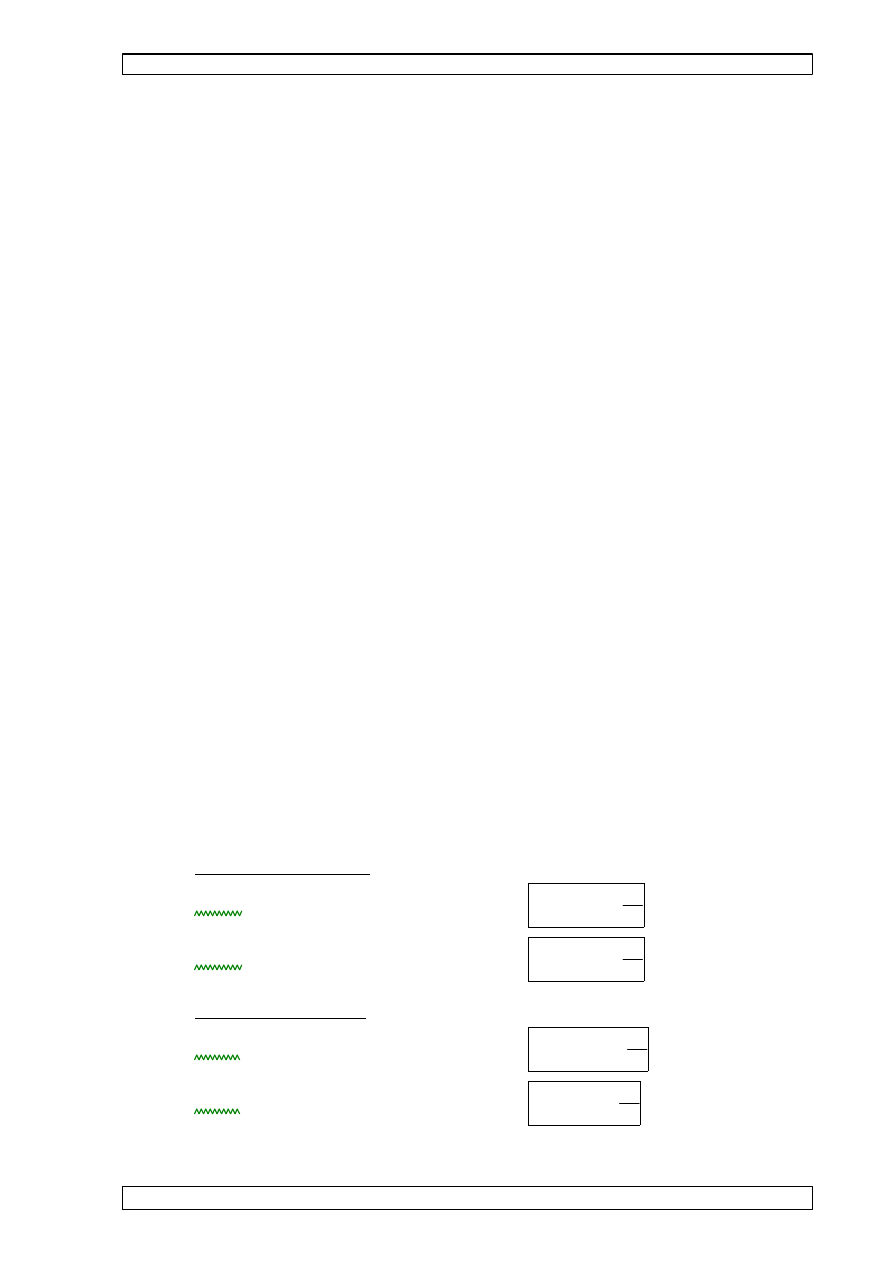
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

KOMBINACJA SGU - max:

•

ppks.y

G1k.y Q1k.y

+

S1k.y

+

:=

ppks.y 3.82

kN

m

⋅

=

ppks.z

G1k.z Q1k.z

+

S1k.z

+

:=

ppks.z 0.24

kN

m

⋅

=

KOMBINACJA SGU - min:

•

ppki.y

G1k.y W1k

+

:=

ppki.y

2.13

−

kN

m

⋅

=

ppki.z

G1k.z

:=

ppki.z 0.04

kN

m

⋅

=

Projektował: Artur Sta

ń

czewski

Strona 55

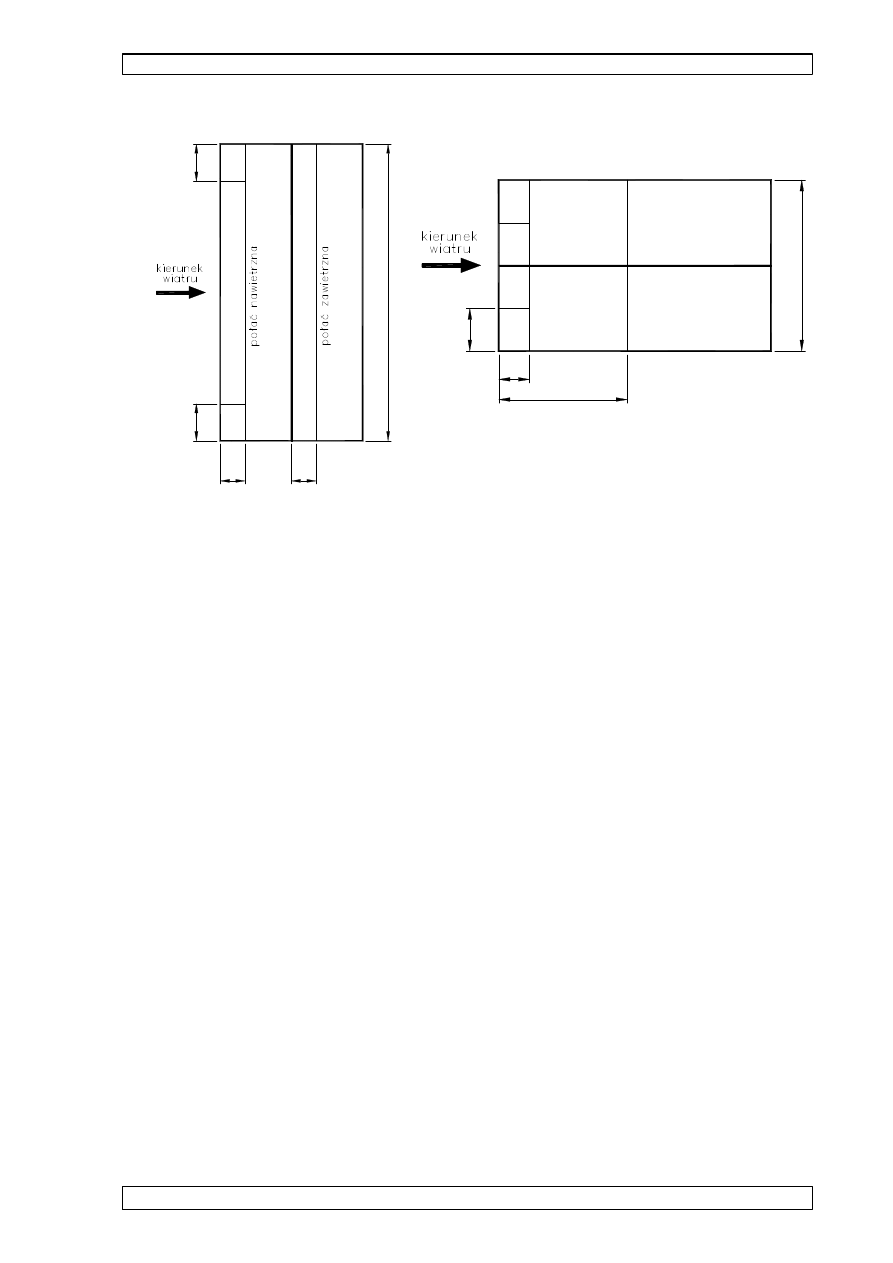
PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

b

F

F

G

H

J

I

e

/4

e/10

e

/4

e/10

F

G

F

G

H

H

I

I

b

e/10

e/2

e

/4

Projektował: Artur Sta

ń

czewski

Strona 56

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

Projektował: Artur Sta

ń

czewski

Strona 57

PROJEKT KONSTRUKCJI DACHU

POLITECHNIKA KRAKOWSKA

Projektował: Artur Sta

ń

czewski

Strona 58