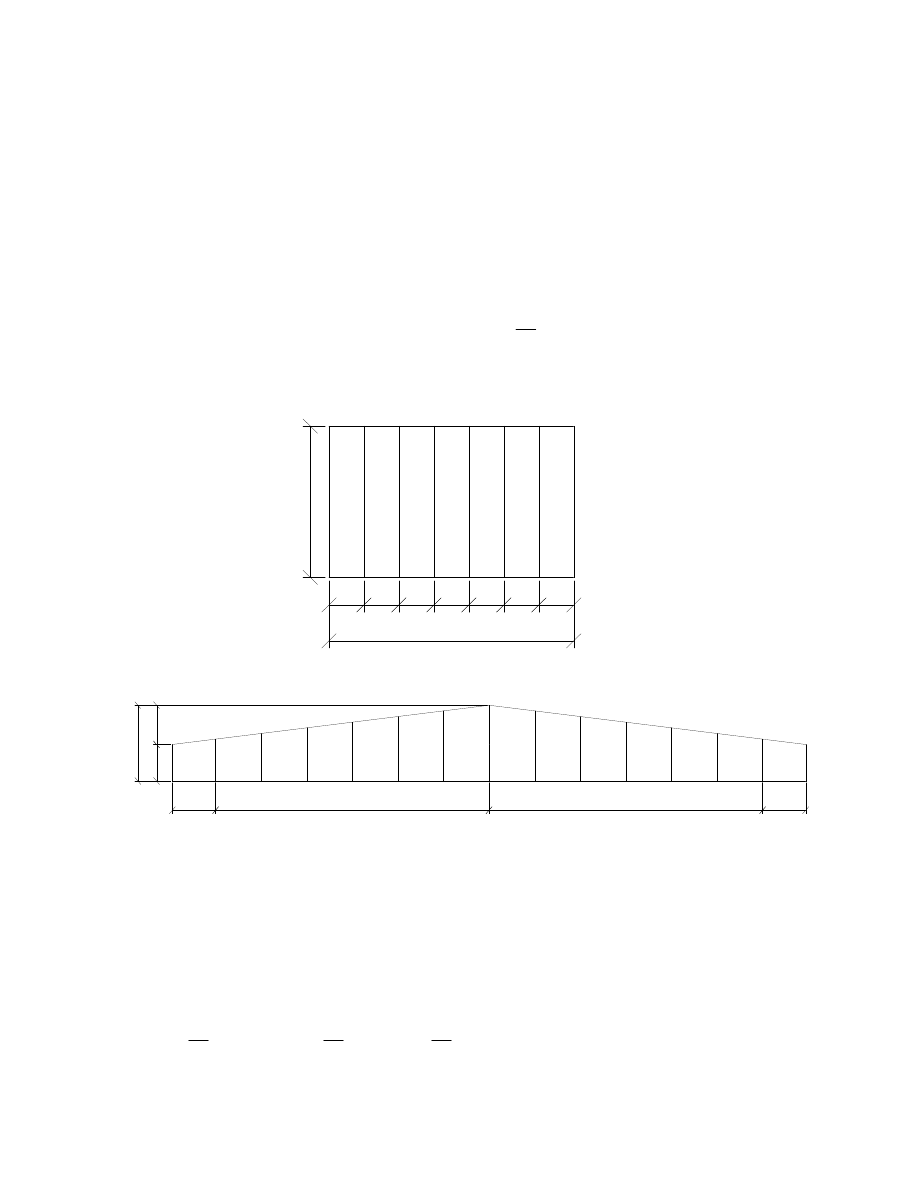
Projekt dachu kratowego

Dane:

rozpieto

ść

długo

ść

lokalizacja

wys. u

ż

ytkowa

k

ą

t nachylenia

stal

b

26.4m

:=

L

42m

:=

Opole

h

uż

5m

:=

α

6.054deg

:=

S235

płyta dachowa: Metalplast ISOTHERM D140/100 (c.w. 0.133

kN

m

2

)

6

6

6

6

6

6

6

2

6

,4

42

1800

6 x 1900

6 x 1900

1800

1

3

0

0

1

4

0

0

2

7

0

0

q

k1

0

kN

m

:=

q

k2

0

kN

m

:=

q

k5

0

kN

m

:=

sk

ą

d si

ę

bior

ą

?

1. Obci

ąż

enia stałe

1.1. Ci

ęż

ar własny elementów konstrukcyjnych (warto

ść

chrakterystyczna obci

ąż

enia)

a

6m

:=

rozstaw ram

q

k3

0.1

kN

m

2

a

⋅

0.6

kN

m

⋅

=

:=

1.2. Ci

ęż

ar własny pokrycia dachowego (warto

ść

charakterystyczna obci

ąż

enia)

q

k4

0.133

kN

m

2

a

⋅

0.798

kN

m

⋅

=

:=

1.3. Współczynniki cz

ęś

ciowe dla oddziaływa

ń

stałych przy obliczaniu górnej/dolnej

warto

ś

ci obliczeniowej

γ

g.sup

1.35

:=

γ

g.inf

1.00

:=

1.4. Górne/dolne warto

ś

ci obliczeniowe obci

ąż

e

ń

stałych

q

d1.sup

q

k1

γ

g.sup

⋅

0

kN

m

⋅

=

:=

q

d2.sup

q

k2

γ

g.sup

⋅

0

kN

m

⋅

=

:=

q

d1.inf

q

k1

γ

g.inf

⋅

0

kN

m

⋅

=

:=

q

d2.inf

q

k2

γ

g.inf

⋅

0

kN

m

⋅

=

:=

2. Obci

ąż

enia zmienne klimatyczne

2.1 Obci

ąż

enie

ś

niegiem (PN-EN 1991-1-3

> Opole, strefa obci

ąż

enia gruntu 2 (rys. NB.1)

2.1.1. Obci

ąż

enie

ś

niegiem gruntu

s

k

0.9

kN

m

2

:=

warto

ść

charakterystyczna obci

ąż

enia

2.1.2. Obci

ąż

enie

ś

niegiem dachu

> Przyj

ę

to dach dwupołaciowy, symetryczny, o k

ą

cie nachylenia połaci

α

6.054 deg

⋅

=

> Dach nie posiada attyki ani barierek przeciw

ś

nie

ż

nych dlatego nie ma konieczno

ś

ci

uwzgl

ę

dniania obci

ąż

e

ń

miejscowych

> Przyjmuj

ę

,

ż

e obci

ąż

enie działa pionowo na obszarze rzutu dachu na płaszczyzn

ę

poziom

ą

Wyznaczenie warto

ś

ci charakterystycznej obci

ąż

enia

ś

niegiem dachu

μ

1

0.8

:=

współczynnik kształtu dachu, taka warto

ść

dla

0deg

α

<

30deg

<

1

=

C

e

1

:=

współczynnik ekspozycji dla terentu normalnego (Tablica 5.1

C

t

1

:=

współczynnik termiczny dla dachów które nie maj

ą

wysokiego współczynnika

przenikania ciepła (p. 5.2 (8))

s

k

0.9

kN

m

2

⋅

=

obci

ąż

enie

ś

niegiem gruntu

s

μ

1

C

e

⋅

C

t

⋅

s

k

⋅

0.72

kN

m

2

⋅

=

:=

2.1.3. Obci

ąż

enie

ś

niegiem ramy po

ś

redniej (warto

ś

ci charakterystyczne)

Przypadki obci

ąż

eniowe

I)

s

rkI

s a

⋅

4.32

kN

m

⋅

=

:=

II)

s

rkII

s a

⋅

4.32

kN

m

⋅

=

:=

1

2

s

rkII

⋅

2.16

kN

m

⋅

=

III)

1

2

s

rkIII

⋅

2.16

⋅

=

s

rkIII

4.32

kN

m

:=

2.2. Obci

ąż

enie wiatrem (PN-EN 1991-1-4)

> Opole - 1 strefa obci

ąż

enia wiatrem (rys. NA.1) A = 183.1 m npm st

ą

d:

v

b.0

22

m

s

:=

warto

ść

podstawowa bazowej pr

ę

dko

ś

ci wiatru

q

b.0

0.30

kN

m

2

:=

warto

ść

podstawowa ci

ś

nienia pr

ę

dko

ś

ci wiatru

> bazowa pr

ę

dko

ść

wiatru (p. 4.2)

C

dir

1

:=

współczynnik kierunkowy, przyj

ą

łem warto

ść

najbardziej niekorzystn

ą

wg. Tabl. NA.2, zakładaj

ą

c kierunek wiatru 270 - 300 stopni (1 strefa wiatrowa)

C

season

1

:=

współczynnik sezonowy (wg NA.4)

v

b

22

m

s

:=

> teren kategorii III (teren podmiejski) wg Tabl. 4.1., st

ą

d:

z

0

0.3m

:=

wymiar chropowato

ś

ci

z

min

5m

:=

wys. minimalna

> współczynnik chropowato

ś

ci dla terenu kat. III

z

h

uż

2.7m

+

7.7 m

=

:=

C

r

0.8

z

10m













0.19

⋅

0.761

=

:=

> współczynnik orografii (rze

ź

by terenu)

przyj

ę

to,

ż

e teren jest płaski lub poło

ż

ony na bardzo łagodnie wypi

ę

trzonym wzniesieniu, czyli

nie ma konieczno

ś

ci zwi

ę

kszenia pr

ę

dko

ś

ci wiatru ze wzgl

ę

du na ukształtowanie terenu

C

0

1.0

:=

>

ś

rednia pr

ę

dko

ść

wiatru (p. 4.3)

V

m

C

r

C

0

⋅

v

b

⋅

16.747

m

s

⋅

=

:=

> warto

ść

szczytowa ci

ś

nienia pr

ę

dko

ś

ci (p. 4.5)

ρ

1.25

kg

m

3

:=

g

ę

sto

ść

powietrza, zale

ż

na od wysoko

ś

ci nad poziomem morza, temperatury

i ci

ś

nienia atmosferycznego, wyst

ę

puj

ą

ca w rozwa

ż

anym regionie w czasie

silnego wiatru. Przyjmuj

ę

warto

ść

zalecan

ą

. (UWA GA 2, 4.10)

q

b

1

2

ρ

⋅

v

b

2

⋅

:=

warto

ść

bazowa ci

ś

nienia pr

ę

dko

ś

ci

q

b

302.5Pa

:=

C

e

1.9

z

10m













0.26

1.775

=

:=

współczynnik ekspozycji, dla terenu kat. III

q

p

C

e

q

b

⋅

536.99 Pa

⋅

=

:=

2.2.1. Obci

ąż

enie wiatrem ramy po

ś

redniej (warto

ś

ci charakterystyczne)

> Rozpatrzono wiatr działaj

ą

cy prostopadle do osi podłu

ż

nej budynku

> Ci

ś

nienie sumaryczne (netto), działaj

ą

ce na

ś

cian

ę

lub dach, jest ró

ż

nic

ą

algebraiczn

ą

mi

ę

dzy

warto

ś

ciami ci

ś

nienia po obu stronach przegrody.

Parcie, skierowane ku powierzchni, jest przyjmowane jako dodatnie (pos), a ssanie skierowane
od powierzchni, jako ujemne (neg)

> Obci

ąż

enie wiatrem nale

ż

y przyjmowa

ć

jako prostopadłe do powierzchni, na któr

ą

działa

2.2.1.1 Obci

ąż

enie słupów ram po

ś

rednich (te obliczenia RACZEJ niepotrzebne)

> ci

ś

nienie działaj

ą

ce na powierzchnie zewn

ę

trzne

z

eD

h

uż

5 m

=

:=

wysoko

ść

odniesienia dla

ś

ciany nawietrznej (strefa D)

z

eE

z

7.7 m

=

:=

wys. odniesienia dla

ś

ciany zawietrznej (strefa E)

b

e

L

42 m

=

:=

szeroko

ść

ś

ciany nawietrznej i zawietrznej

h

uż

b

1

<

1

=

z

b

1

<

1

=

szeroko

ść

ś

ciany mniejsza od jej wysoko

ś

ci, zatem zarówno

dla

ś

ciany nawietrznej, jak i zawietrznej, mo

ż

na przyj

ąć

stałe

na wysoko

ś

ci

ś

ciany ci

ś

nienie pr

ę

dko

ś

ci, wyznaczone dla

wysoko

ś

ci odniesienia jak wy

ż

ej:

ś

ciana nawietrzna (strefa D)

ś

ciana zawietrzna (strefa E)

C

eD

1.9

z

eD

10m













0.26

1.587

=

:=

C

eE

1.9

z

eE

10m













0.26

1.775

=

:=

q

pD

C

eD

q

b

⋅

479.967 Pa

⋅

=

:=

q

pE

C

eE

q

b

⋅

536.99 Pa

=

:=

> warto

ś

ci współczynnika ci

ś

nienia zewn

ę

trznego

C

pe

dla

ś

cian pionowych budynków na rzucie

prostok

ą

ta (Tabl. 7.1)

Zgodnie z p.7.2.1(1) Uwaga 1 w obliczeniach konstrukcji no

ś

nych budynków jako cało

ś

ci mog

ą

by

ć

u

ż

ywane warto

ś

ci Cpe,10.

d

b

26.4 m

=

:=

wymiar budynku równoległy do kierunku działania wiatru

ś

ciana nawietrzna (strefa D)

z

eD

d

0.189

=

=>

C

peD.10

0.7

:=

ś

ciana zawietrzna (strefa E)

z

eE

d

0.292

=

=>

C

peE.10

0.312

−

:=

> Ci

ś

nienie zewn

ę

trzne działaj

ą

ce na powierzchni

ę

ś

ciany nawietrznej (strefa D):

w

eD

q

pD

C

peD.10

⋅

335.977 Pa

=

:=

> Ci

ś

nienie zewn

ę

trzne działaj

ą

ce na powierzchni

ę

ś

ciany zawietrznej (strefa E):

w

eE

q

pE

C

peE.10

⋅

167.541

−

Pa

=

:=

> Ci

ś

nienie działaj

ą

ce na powierzchnie wewn

ę

trzne

q

pi

q

p

536.99 Pa

=

:=

z

i

z

eE

7.7 m

=

:=

C

pi.p

0.3

−

:=

na potrzeby projektu przyjmujemy zało

ż

enie, i

ż

wewn

ą

trz budynku panuje

podci

ś

nienie, st

ą

d:

w

i

q

pi

C

pi.p

⋅

:=

ś

ciana nawietrzna (strefa D)

w

iD.p

q

pD

C

pi.p

⋅

143.99

−

Pa

=

:=

ś

ciana zawietrzna (strefa E)

w

iE.p

q

pE

C

pi.p

⋅

161.097

−

Pa

=

:=

Przypadki obci

ąż

enia słupów ram po

ś

rednich

w naszym projekcie taki przypadek nie obowi

ą

zuje poniewa

ż

ś

cianka jest osłoni

ę

ta od wiatru

2.2.1.2. Obci

ąż

enie rygli ram po

ś

rednich

> Ci

ś

nienie działaj

ą

ce na powierzchnie zewn

ę

trzne

w

e

q

pE

C

e

⋅

953.252 Pa

=

:=

> Obliczenia s

ą

prowadzone dla stref G, H, J, I (rys. 7.8)

e

min b 2z

,

(

)

15.4 m

=

:=

st

ą

d szeroko

ść

stref przykraw

ę

dziowych:

e

10

1.54 m

=

Dla k

ą

ta nachylenia połaci dachowej

α

6.054 deg

⋅

=

interpoluj

ę

warto

ś

ci

C

pe.10

z tablicy 7.4a

i otrzymałem:

1) Strefa G:

C

pe.10.GI

1.16

−

:=

lub

C

pe.10.GII

0.02

:=

2) Strefa H:

C

pe.10.HI

0.57

−

:=

lub

C

pe.10.HII

0.02

:=

3) Strefa J:

C

pe.10.JI

0.07

:=

lub

C

pe.10JII

0.54

−

:=

4) Strefa I:

C

pe.10.II

0.58

−

:=

lub

C

pe.10.III

0.54

−

:=

Zgodnie z Tabl. 7.1. Uwaga 1 nale

ż

y rozwa

ż

y

ć

cztery przypadki, w których najwi

ę

ksze albo najmniejsze

warto

ś

ci we wszystkich polach G i H wyst

ę

puj

ą

ł

ą

cznie z najwi

ę

kszymi warto

ś

ciami w polach I i J.

Nie dopuszcza si

ę

jednoczesnego przyjmowania warto

ś

ci dodatnich i ujemnych na tej samej połaci.

1) max GH i max JI

C

pe.10.G1

max C

pe.10.GI

C

pe.10.GII

,

(

)

0.02

=

:=

C

pe.10.J1

max C

pe.10.JI

C

pe.10JII

,

(

)

0.07

=

:=

C

pe.10.H1

max C

pe.10.HI

C

pe.10.HII

,

(

)

0.02

=

:=

C

pe.10.I1

max C

pe.10.II

C

pe.10.III

,

(

)

0.54

−

=

:=

w tym przypadku wyst

ę

puj

ą

zarówno warto

ś

ci

dodatnie jak i ujemne na tej samej połaci
dlatego przypadek 1 odrzucam w dalszych rozwa

ż

aniach

2) max GH i min JI

C

pe.10.G2

max C

pe.10.GI

C

pe.10.GII

,

(

)

0.02

=

:=

C

pe.10.J2

min C

pe.10.JI

C

pe.10JII

,

(

)

0.54

−

=

:=

C

pe.10.H2

max C

pe.10.HI

C

pe.10.HII

,

(

)

0.02

=

:=

C

pe.10.I2

min C

pe.10.II

C

pe.10.III

,

(

)

0.58

−

=

:=

3) min GH i max JI

C

pe.10.G3

min C

pe.10.GI

C

pe.10.GII

,

(

)

1.16

−

=

:=

C

pe.10.J3

max C

pe.10.JI

C

pe.10JII

,

(

)

0.07

=

:=

C

pe.10.H3

min C

pe.10.HI

C

pe.10.HII

,

(

)

0.57

−

=

:=

C

pe.10.I3

max C

pe.10.II

C

pe.10.III

,

(

)

0.54

−

=

:=

w tym przypadku wyst

ę

puj

ą

zarówno warto

ś

ci

dodatnie jak i ujemne na tej samej połaci
dlatego przypadek 3 odrzucam w dalszych rozwa

ż

aniach

4) min GH i min JI

C

pe.10.G4

min C

pe.10.GI

C

pe.10.GII

,

(

)

1.16

−

=

:=

C

pe.10.J4

min C

pe.10.JI

C

pe.10JII

,

(

)

0.54

−

=

:=

C

pe.10.H4

min C

pe.10.HI

C

pe.10.HII

,

(

)

0.57

−

=

:=

C

pe.10.I4

min C

pe.10.II

C

pe.10.III

,

(

)

0.58

−

=

:=

> Ci

ś

nienie działaj

ą

ce na powierzchnie zewn

ę

trzne

2) max GH i min JI

4) min GH i min JI

w

eG.max2

q

pE

C

pe.10.G2

⋅

10.74 Pa

=

:=

w

eG.min4

q

pE

C

pe.10.G4

⋅

622.909

−

Pa

=

:=

w

eH.max2

q

pE

C

pe.10.H2

⋅

10.74 Pa

=

:=

w

eH.min4

q

pE

C

pe.10.H4

⋅

306.085

−

Pa

=

:=

w

eJ.min2

q

pE

C

pe.10.J2

⋅

289.975

−

Pa

=

:=

w

eJ.min4

q

pE

C

pe.10.J4

⋅

289.975

−

Pa

=

:=

w

eI.min2

q

pE

C

pe.10.I2

⋅

311.454

−

Pa

=

:=

w

eI.min4

q

pE

C

pe.10.I4

⋅

311.454

−

Pa

=

:=

> ci

ś

nienie działaj

ą

ce na powierzchnie wewn

ę

trzne dachu

Przyjmuj

ę

jak dla powierzchni wewn

ę

trznej

ś

ciany zawietrznej

C

pi.p

0.3

−

=

podciśnienie

z

i

7.7 m

=

w

i.p

C

pi.p

q

p

⋅

161.097 Pa

=

:=

> Przypadki obci

ąż

enia rygli ram po

ś

rednich

Wewn

ą

trz budynku panuje podci

ś

nienie

2) WRP2: max GH i min JI

4) WRP4: min GH i min JI

w

G.p2

w

eG.max2

w

i.p

+

(

)

a

⋅

1.031

kN

m

⋅

=

:=

w

G.p4

w

eG.min4

w

i.p

+

(

)

a

⋅

2.771

−

kN

m

⋅

=

:=

w

H.p2

w

eH.max2

w

i.p

+

(

)

a

⋅

1.031

kN

m

⋅

=

:=

w

H.p4

w

eH.min4

w

i.p

+

(

)

a

⋅

0.87

−

kN

m

⋅

=

:=

w

J.p2

w

eJ.min2

w

i.p

+

(

)

a

⋅

0.773

−

kN

m

⋅

=

:=

w

J.p4

w

J.p2

0.773

−

kN

m

⋅

=

:=

w

I.p2

w

eI.min2

w

i.p

+

(

)

a

⋅

0.902

−

kN

m

⋅

=

:=

w

I.p4

w

I.p2

0.902

−

kN

m

⋅

=

:=

2.3. Współczynniki cz

ęś

ciowe dla oddziaływa

ń

zmiennych (PN-EN 1990)

Zgodnie z Tabl. A.1.2(B)

γ

Q.1

1.5

:=

je

ż

eli niekorzystne (0 je

ż

eli korzystne)

γ

Q.2

1.5

:=

je

ż

eli niekorzystne (0 je

ż

eli korzystne)

Kombinacje obci

ąż

en działaj

ą

cych na ram

ę

po

ś

redni

ą

(PN-EN 1990)

Kombinacje SGU

Wprowadzam nast

ę

puj

ą

ce oznaczenia:

G

k

sumaryczne obci

ąż

enie stałe działaj

ą

ce na ram

ę

q

k1

q

k2

+

q

k3

+

q

k4

+

q

k5

+

(

)

Q

s1

obci

ąż

enie

ś

niegiem działaj

ą

ce w przypadku obci

ąż

eniowym S1

Q

s2

obci

ąż

enie

ś

niegiem działaj

ą

ce w przypadku obci

ąż

eniowym S2

Q

s3

obci

ąż

enie

ś

niegiem działaj

ą

ce w przypadku obci

ąż

eniowym S3

Q

w1

obci

ąż

enie wiatrem działaj

ą

ce w przypadku obci

ąż

eniowym WRP2

Q

w2

obci

ąż

enie wiatrem działaj

ą

ce w przypadku obci

ąż

eniowym WRP4

UWAGA :

Zało

ż

ono,

ż

e konstrukcja jest symetryczna, w wzi

ą

zku z czym rozpatrywałem

obci

ąż

enie wiatrem wiej

ą

cym tylko z jednego kierunku. Pomini

ę

to wiatr

wiej

ą

cy z kierunku przeciwnego.

Zgodnie z Tabl. A1.1 i Tabl. A.1.2(b) przyj

ę

to nastepuj

ą

ce warto

ś

ci ws półc zynnik ów

Obci

ąż

enie stałe:

γ

G.max

γ

g.sup

1.35

=

:=

γ

G.min

γ

g.inf

1

=

:=

ξ

0.85

:=

Obci

ąż

enia zmienne -

ś

nieg (S) i wiatr (W)

γ

Q.S

1.5

:=

je

ż

eli niekorzystne (0 je

ś

li korzystne)

γ

Q.W

1.5

:=

je

ż

eli niekorzystne (0 je

ś

li korzystne)

ψ

0.S

0.5

:=

ψ

0.W

0.5

:=

Rozpisuj

ą

c wyra

ż

enia (6.10a) i (6.10b) dla rozpatrywanych w niniejszym przykładzie przypadków

obci

ąż

e

ń

otrzymano (por. Tabl. A1.2(B))

1)

G

max

i

Q

s

Q

s1

(

albo Q

s2

albo

Q

s3

) =>

6 kombinacji obci

ąż

e

ń

a)

γ

G.max

G

k

⋅

γ

Q.S

ψ

0.S

⋅

Q

s

⋅

+

b)

ξ γ

G.max

⋅

G

k

⋅

γ

Q.S

Q

S

⋅

+

2)

G

min

i

Q

w

Q

w1

(

albo Q

w2

)

=>

4 kombinacje obci

ąż

e

ń

a)

γ

G.min

G

k

⋅

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

b)

γ

G.min

G

k

⋅

γ

Q.W

Q

W

⋅

+

3)

G

max

i

Q

s1

(wiod

ą

ce/główne) i

Q

W

Q

w1

(

albo Q

w2

) (towarzysz

ą

ce)

=>

4 kombinacje obci

ąż

e

ń

a)

γ

G.max

G

k

⋅

γ

Q.S

ψ

0.S

⋅

Q

s1

⋅

+

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

b)

ξ γ

G.max

⋅

G

k

⋅

γ

Q.S

Q

S1

⋅

+

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

4)

G

max

i

Q

s2

(wiod

ą

ce/główne) i

Q

W

Q

w1

(

albo Q

w2

) (towarzysz

ą

ce)

=>

4 kombinacje obci

ąż

e

ń

a)

γ

G.max

G

k

⋅

γ

Q.S

ψ

0.S

⋅

Q

s2

⋅

+

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

b)

ξ γ

G.max

⋅

G

k

⋅

γ

Q.S

Q

S2

⋅

+

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

5)

G

max

i

Q

s3

(wiod

ą

ce/główne) i

Q

W

Q

w1

(

albo Q

w2

) (towarzysz

ą

ce)

=>

4 kombinacje obci

ąż

e

ń

a)

γ

G.max

G

k

⋅

γ

Q.S

ψ

0.S

⋅

Q

s3

⋅

+

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

b)

ξ γ

G.max

⋅

G

k

⋅

γ

Q.S

Q

S3

⋅

+

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

6)

G

min

i

Q

s1

(wiod

ą

ce/główne) i

Q

W

Q

w1

(

albo Q

w2

) (towarzysz

ą

ce)

=>

4 kombinacje obci

ąż

e

ń

a)

γ

G.min

G

k

⋅

γ

Q.S

ψ

0.S

⋅

Q

s1

⋅

+

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

b)

ξ γ

G.min

⋅

G

k

⋅

γ

Q.S

Q

S1

⋅

+

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

7)

G

min

i

Q

s2

(wiod

ą

ce/główne) i

Q

W

Q

w1

(

albo Q

w2

) (towarzysz

ą

ce)

=>

4 kombinacje obci

ąż

e

ń

a)

γ

G.min

G

k

⋅

γ

Q.S

ψ

0.S

⋅

Q

s2

⋅

+

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

b)

ξ γ

G.min

⋅

G

k

⋅

γ

Q.S

Q

S2

⋅

+

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

8)

G

min

i

Q

s3

(wiod

ą

ce/główne) i

Q

W

Q

w1

(

albo Q

w2

) (towarzysz

ą

ce)

=>

4 kombinacje obci

ąż

e

ń

a)

γ

G.min

G

k

⋅

γ

Q.S

ψ

0.S

⋅

Q

s3

⋅

+

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

b)

ξ γ

G.min

⋅

G

k

⋅

γ

Q.S

Q

S3

⋅

+

γ

Q.W

ψ

0.W

⋅

Q

W

⋅

+

9)

G

max

i

Q

W1

(wiod

ą

ce/główne) i

Q

s

Q

s1

(

albo albo

Q

s2

albo

Q

s3

) (towarzysz

ą

ce)

=>

6 kombinacji obci

ąż

e

ń

a)

γ

G.max

G

k

⋅

γ

Q.W

ψ

0.W

⋅

Q

W1

⋅

+

γ

Q.S

ψ

0.S

⋅

Q

S

⋅

+

b)

ξ γ

G.max

⋅

G

k

⋅

γ

Q.W

Q

W1

⋅

+

γ

Q.S

ψ

0.S

⋅

Q

S

⋅

+

10)

G

max

i

Q

W2

(wiod

ą

ce/główne) i

Q

s

Q

s1

(

albo albo

Q

s2

albo

Q

s3

) (towarzysz

ą

ce)

=>

6 kombinacji obci

ąż

e

ń

a)

γ

G.max

G

k

⋅

γ

Q.W

ψ

0.W

⋅

Q

W2

⋅

+

γ

Q.S

ψ

0.S

⋅

Q

S

⋅

+

b)

ξ γ

G.max

⋅

G

k

⋅

γ

Q.W

Q

W2

⋅

+

γ

Q.S

ψ

0.S

⋅

Q

S

⋅

+

11)

G

min

i

Q

W1

(wiod

ą

ce/główne) i

Q

s

Q

s1

(

albo albo

Q

s2

albo

Q

s3

) (towarzysz

ą

ce)

=>

6 kombinacji obci

ąż

e

ń

a)

γ

G.min

G

k

⋅

γ

Q.W

ψ

0.W

⋅

Q

W1

⋅

+

γ

Q.S

ψ

0.S

⋅

Q

S

⋅

+

b)

ξ γ

G.min

⋅

G

k

⋅

γ

Q.W

Q

W1

⋅

+

γ

Q.S

ψ

0.S

⋅

Q

S

⋅

+

12)

G

min

i

Q

W2

(wiod

ą

ce/główne) i

Q

s

Q

s1

(

albo albo

Q

s2

albo

Q

s3

) (towarzysz

ą

ce)

=>

6 kombinacji obci

ąż

e

ń

a)

γ

G.min

G

k

⋅

γ

Q.W

ψ

0.W

⋅

Q

W2

⋅

+

γ

Q.S

ψ

0.S

⋅

Q

S

⋅

+

b)

ξ γ

G.min

⋅

G

k

⋅

γ

Q.W

Q

W2

⋅

+

γ

Q.S

ψ

0.S

⋅

Q

S

⋅

+

Ł

ą

cznie (przy zało

ż

eniu symetrii konstrukcji) otrzymano 58 kombinacji dla SGN

Kombinacje SGU

Kombinacja cz

ę

sta (odwracalne stany graniczne) - wzór (6.15b)

Zgodnie z Tabl. A1.1 przyj

ę

to nast

ę

puj

ą

ce warto

ś

ci współczynników:

Obci

ąż

enia zmienne -

ś

nieg (S) i wiatr (W):

ψ

1.S

0.2

:=

ψ

2.S

0.0

:=

ψ

1.W

0.2

:=

ψ

2.W

0.0

:=

Rozpisuj

ą

c wyra

ż

enie (6.15b) dla rozpatrywanych w niniejszym przykładzie przypadków obci

ąż

e

ń

i podanych powy

ż

ej warto

ś

ci współczynników otrzymano (oznaczenia jak dla kombinacji SGU)

1)

G i

Q

s

Q

s1

(

albo albo

Q

s2

albo

Q

s3

) (wiod

ą

ce/główne)

i

Q

W

Q

w1

(

albo Q

w2

)

(towarzysz

ą

ce) => 3 komb. obc.

G

k

ψ

1.S

Q

S

⋅

+

ψ

2.W

Q

W

⋅

+

G

k

ψ

1.S

Q

S

⋅

+

⋅

=

2) G i

Q

W

Q

w1

(

albo Q

w2

) (wiod

ą

ce/główne) i

Q

s

Q

s1

(

albo albo

Q

s2

albo

Q

s3

)

(towarzysz

ą

ce)

=>

2 kombinacje obci

ąż

e

ń

Ł

ą

cznie (przy zało

ż

eniu symetrii konstrukcji) otrzymano 5 kombinacji dla SGU