I. Obliczenia statyczne:
1.Dane:
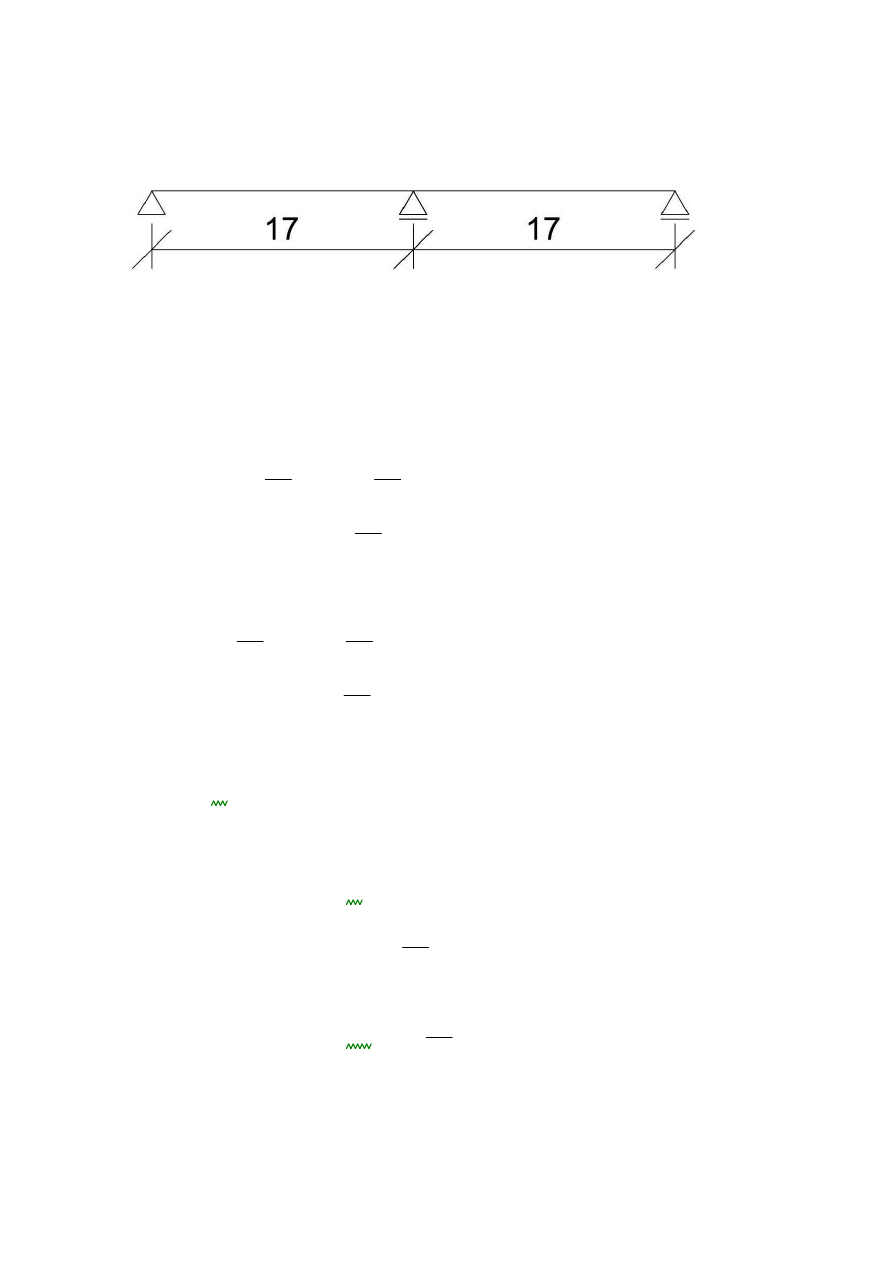
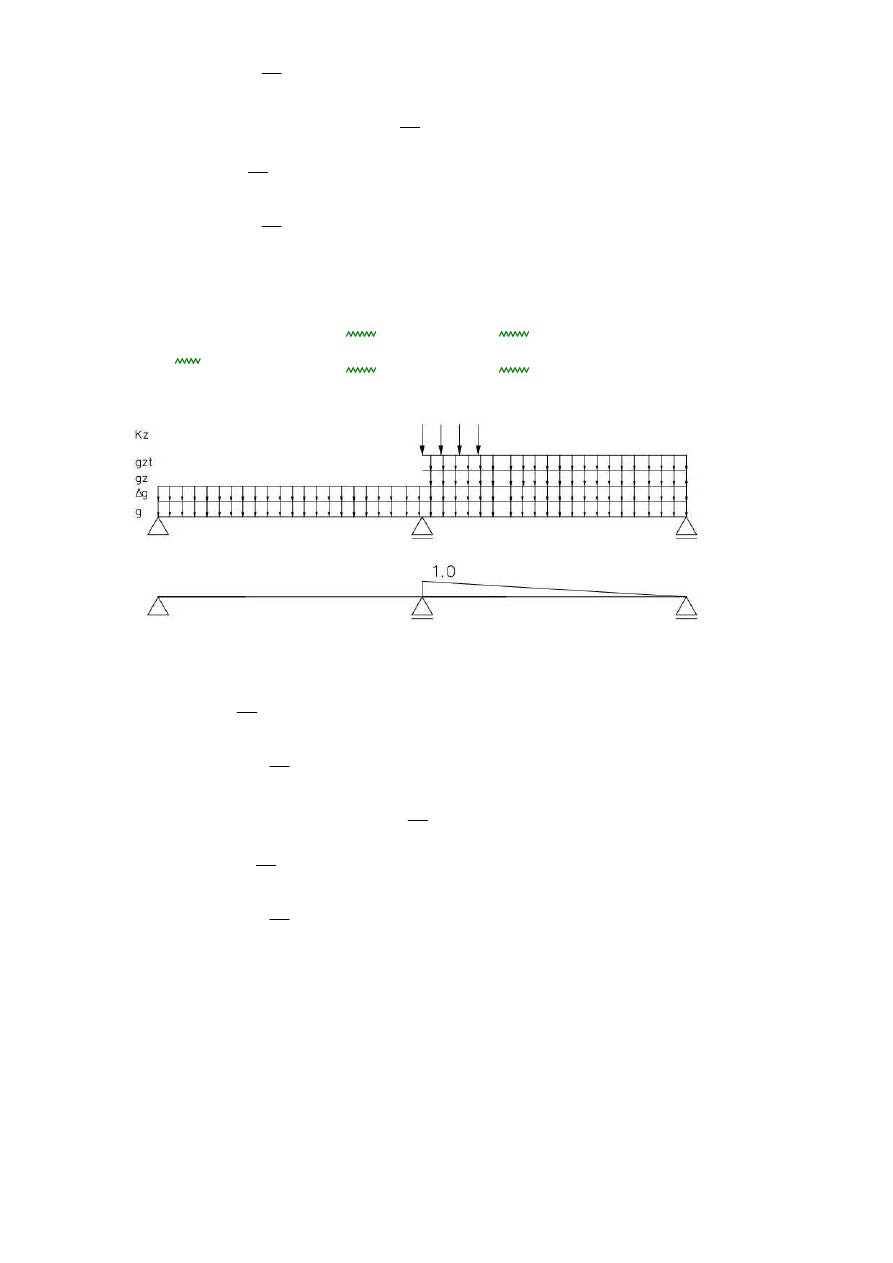
1.1. Schemat statyczny:
1.2. Przekrój poprzeczny
1.3. Klasa obciążeń: A
2. Zestawienie obciążeń:
2.1. Obciążenie stałe konstrukcyjne:
Ciężar własny konstrukcji:
Σgk
90.75
kN
m
90.75
kN
m
⋅
=
:=
Σg
Σgk 1.2
⋅
108.9
kN
m
⋅
=
:=
2.2. Obciążenia stałe niekonstrukcyjne:
Σ∆gk
28.24
kN
m
28.24
kN
m
⋅
=
:=
Σ∆g
Σ∆gk 1.5
⋅
42.36
kN
m
⋅
=
:=
2.3. Obciążenia użytkowe:
2.3.1. Współczynnik dynamiczny:
L
17
:=
ϕ
1.35
0.005 L
⋅
−
1.265
=
:=
2.3.2. Obciążenie taborem samochodowym:
obciążenie
−
K
K
800kN
:=
200kN na oś
100kN na koło
obciążenie
−
q
q
4
kN
m
:=
2.3.3. Obciążenie tłumem pieszych:
obciążenie
−
qt
qt
2.5
kN
m
:=
2.4. Podział poprzeczny obciążeń wg. metody sztywnej poprzecznicy:
Siła jednostkowa
P
1
:=
Liczba dźwigarów
n
2
:=
:=
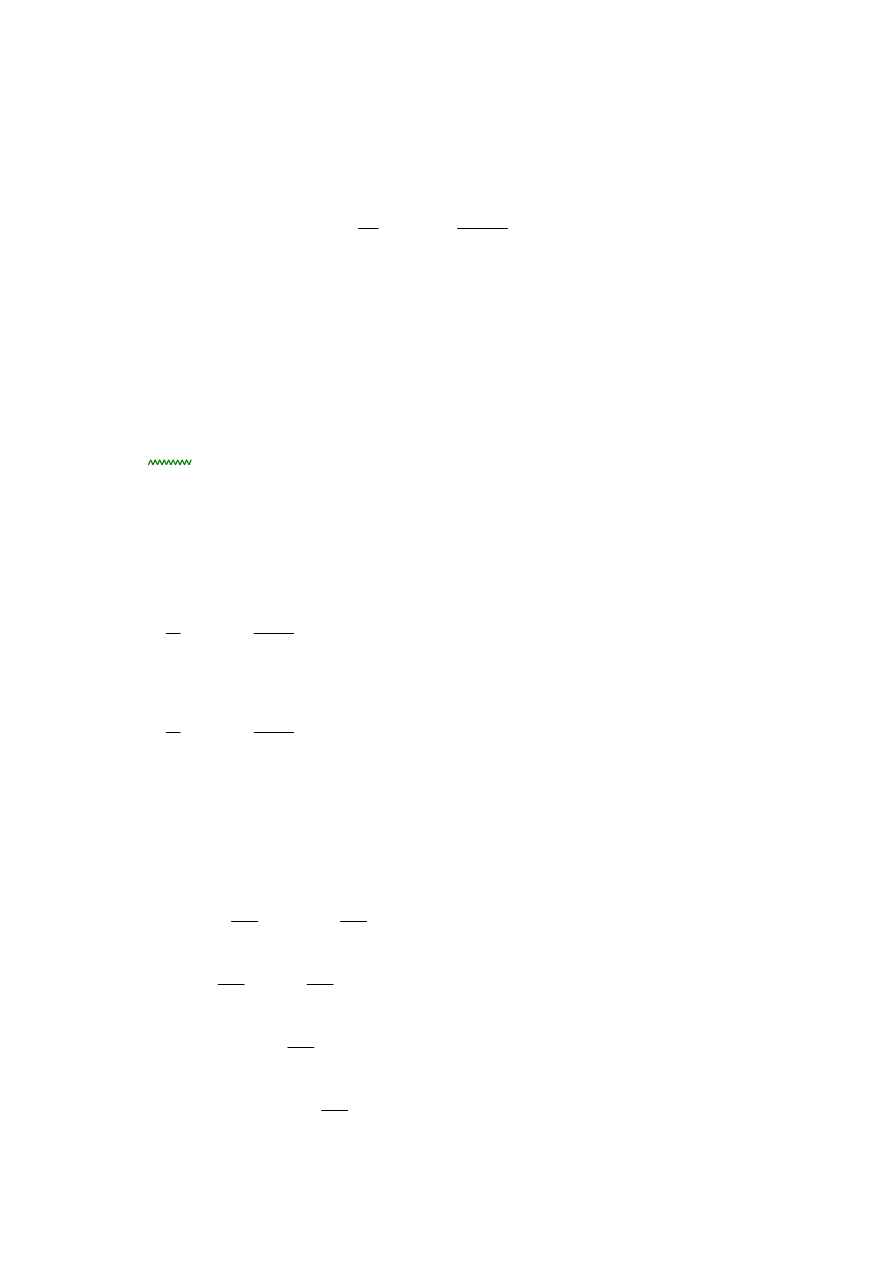
Rozstaw dźwigarów
b0
5.45m
:=
Odległość dźwigara nr 1 od osi
b1
2.725
−
m
:=
Odległość dźwigara nr 2 od osi
b2
2.725m
:=
Obliczenie rzędnych linii wpływu wg wzoru:
Ri
P
ni
P epi
⋅
bi
Σbk
2
⋅
+
:=
P-siła jednostkowa
ep-mimośród działania siły jednostkowej
n- ilośc dźwigarów, n=9
bi-odległość dźwigara od osi
Σbk
b1
2
b2
2
+
14.851 m
2
=
:=
SCHEMAT
Mimośród działania siły jednostkowej:
ep
b1
2.725
−
m
=
:=
Dźwigar
−
nr1
R1
P
n
P ep
⋅
b1
Σbk
⋅
+
1
=
:=
Dźwigar
−
nr2
R2
P
n
P ep
⋅
b2
Σbk
⋅
+
0
=
:=
2.4.2. Obciążenia zastępcze na dźwigar
Obciążenia zastępcze charakterystyczne:
Kzk
193.035kN
193.035 kN
⋅
=
:=
qzk
14.76
kN
m
14.76
kN
m
⋅
=
:=
qztk
7.2
kN
m
7.2
kN
m
⋅
=
:=
gk
Σgk
90.75
kN
m
⋅
=
:=
∆gk
Σ∆gk
28.24
kN
m
⋅
=
:=
Obciążenia zastępcze obliczeniowe:
:=
γfK
1.5
:=
Kz
Kzk γfK
⋅
289.553 kN
⋅
=
:=
γfqz
1.5
:=
qz
qzk γfqz
⋅
22.14
kN
m
⋅
=
:=
γfqtł
1.3
:=
qzt
qztk γfqtł
⋅
9.36
kN
m
⋅
=
:=
γfg
1.2
:=
g
gk γfg
⋅
108.9
kN
m
⋅
=
:=
γf∆g
1.5
:=
∆g
∆gk γf∆g
⋅
42.36
kN
m
⋅
=
:=
3. Wyznaczenie sił wewnętrznych
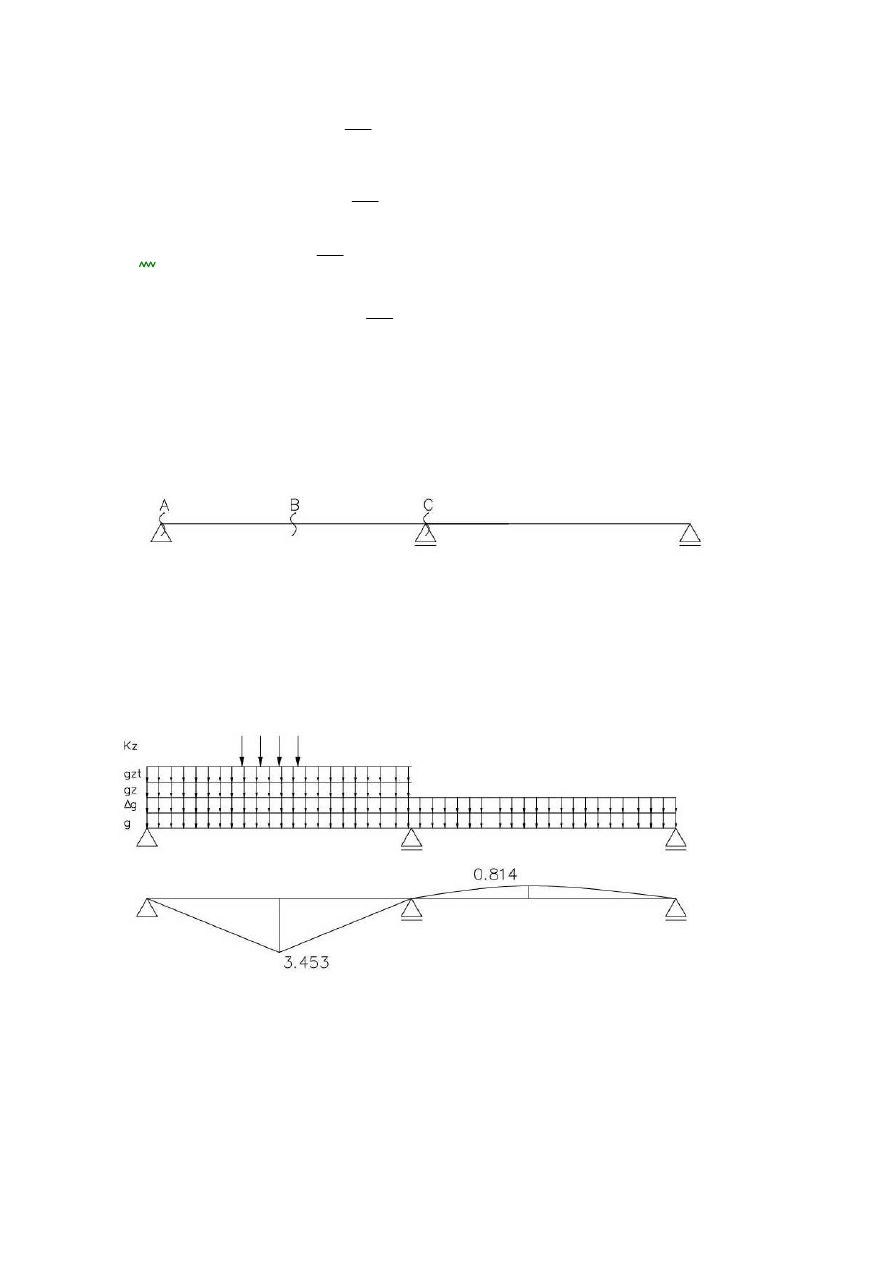
3.1.Przekrój przęsłowy B: linia wpływu momentów zginających wraz z obciążeniami:
F1
29.35m
2
:=
η1
2.388m
:=
η3
3.453m
:=
F2
6.919
−
m
2
:=
η2
2.907m
:=
η4
2.835m
:=
Mbg
g F1
F2
+
(
)
⋅
2.443
10
3
×
kN m
⋅
⋅
=
:=
Mb∆g
∆g F1
F2
+
(
)
⋅
950.177 kN m
⋅
⋅
=
:=
MbKz
Kz η1
η2
+
η3
+
η4
+
(
)
⋅
3.354
10
3
×
kN m
⋅
⋅
=
:=
Mbqz
qz F1
( )
⋅
649.809 kN m
⋅
⋅
=
:=
Mbqzt
qzt F1
( )
⋅
274.716 kN m
⋅
⋅
=
:=
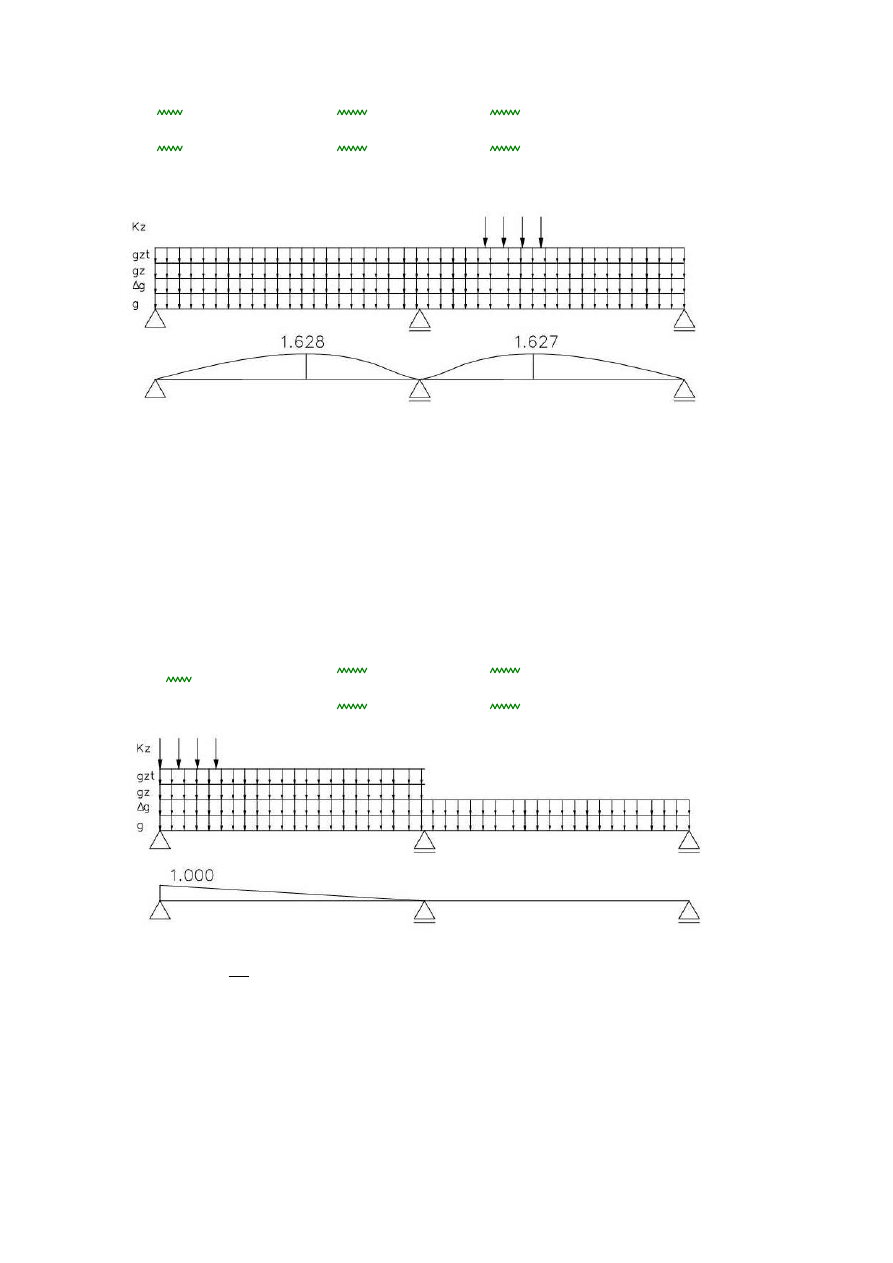
3.2.Przekrój przypodporowy C: linia wpływu momentów zginających wraz z obciążeniami:
F1
17.91
−
m
2
:=
η1
1.611
−
m
:=
η3
1.561
−
m
:=
F2
17.91
−
m
2
:=
η2
1.627
−
m
:=
η4
1.511
−
m
:=
Mcg
g F1
F2
+
(
)
⋅
3.901
−
10
3
×
kN m
⋅
⋅
=
:=
Mc∆g
∆g F1
F2
+
(
)
⋅
1.517
−
10
3
×
kN m
⋅
⋅
=
:=
McKz
Kz η1
η2
+
η3
+
η4
+
(
)
⋅
1.827
−
10
3
×
kN m
⋅
⋅
=
:=
Mcqz
qz F1
F2
+
(
)
⋅
793.055
−
kN m
⋅
⋅
=
:=
Mcqzt
qzt F1
F2
+
(
)
⋅
335.275
−
kN m
⋅
⋅
=
:=
3.3. Przekrój przypodporowy A: Linia wpływu sił tnących wraz z obciążeniami:
η1
1.000m
:=
η3
0.825m
:=
F1
8.5m
2
:=
η2
0.911m
:=
η4
0.738m
:=
Tag
g F1
⋅
1
m
⋅
925.65 kN
⋅
=
:=
Ta∆g
∆g F1
⋅
1
m
⋅
360.06 kN
⋅
=
:=
TaKz
Kz η1
η2
+
η3
+
η4
+
(
)
⋅
1
m
⋅
1.006
10
3
×
kN
⋅
=
:=
Taqz
qz F1
⋅
1
m
⋅
188.19 kN
⋅
=
:=
Taqzt
qzt F1
⋅
1
m
⋅
79.56 kN
⋅
=
:=
3.4. Przekrój przypodporowy C: Linia wpływu sił tnących wraz z obciążeniami:
η1
1.000m
:=
η3
0.914m
:=
F1
8.5m
2
:=
η2
0.960m
:=
η4
0.862m
:=
Tcg
g F1
⋅
1
m
⋅
925.65 kN
⋅
=
:=
Tc∆g
∆g F1
⋅
1
m
⋅
360.06 kN
⋅
=
:=
TcKz
Kz η1
η2
+
η3
+
η4
+
(
)
⋅
1
m
⋅
1.082
10
3
×
kN
⋅
=
:=
Tcqz
qz F1
⋅
1
m
⋅
188.19 kN
⋅
=
:=
Tcqzt
qzt F1
⋅
1
m
⋅
79.56 kN
⋅
=
:=
3.6. Zestawienie momentów i sił tnących w wybranych przekrojach obliczeniowych
(wartości ekstremalne, obliczeniowe):
Mb
Mbg
Mb∆g
+
MbKz
+
Mbqz
+
Mbqzt
+
7.671
10
3
×
kN m
⋅
⋅
=
:=
Mc
Mcg
Mc∆g
+
McKz
+
Mcqz
+
Mcqzt
+
8.374
−
10
3
×
kN m
⋅
⋅
=
:=
Ta
Tag
Ta∆g
+
TaKz
+
Taqz
+
Taqzt
+
2.559
10
3
×
kN
⋅
=
:=
Tc
Tcg
Tc∆g
+
TcKz
+
Tcqz
+
Tcqzt
+
2.635
10
3
×
kN
⋅
=
:=
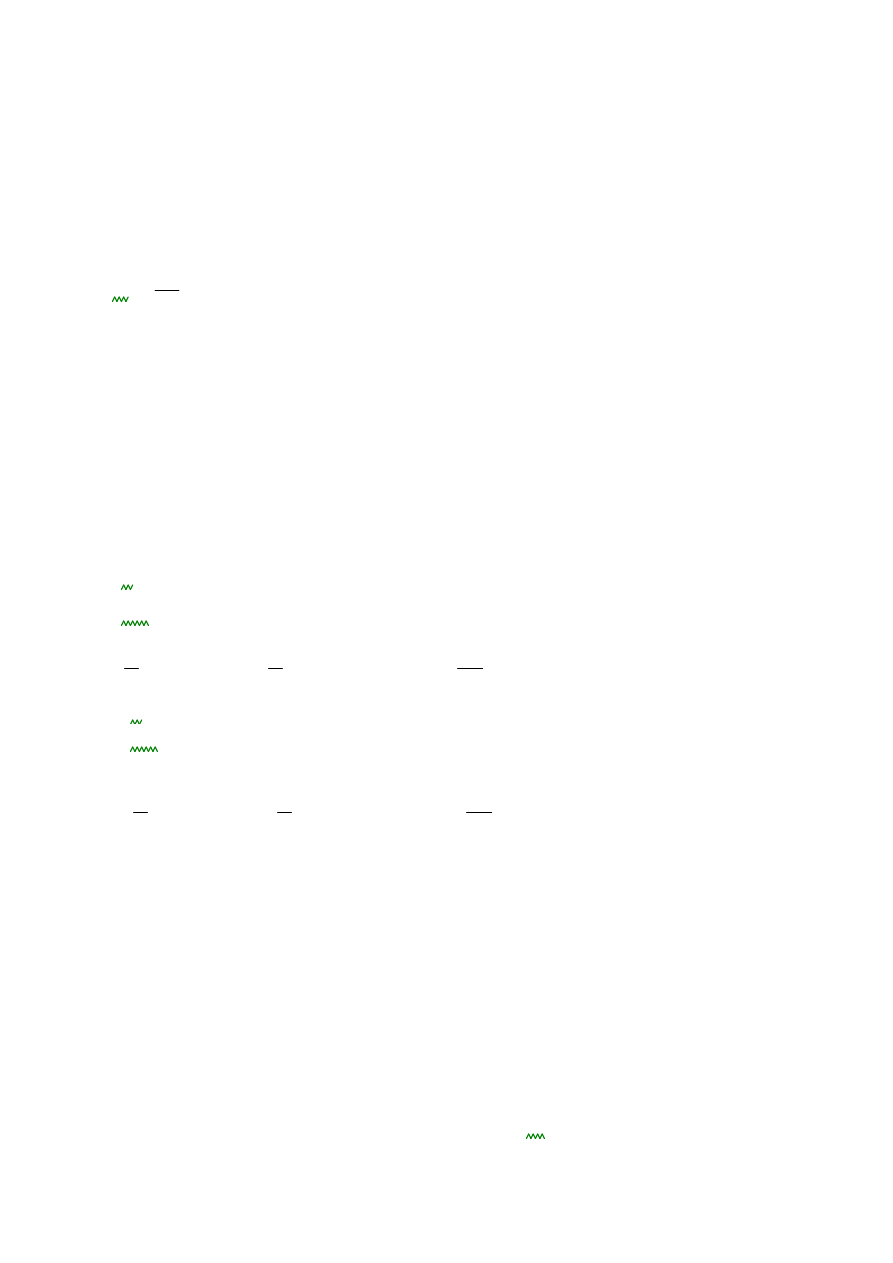
4. Wymiarowanie zbrojenia w dźwigarze głównym-zbrojenie podłużne:
4.1. Dane do wymiarowania:
Beton B50
Rb
28.8MPa
:=
Eb
39GPa
:=
Stal A-IIIN (20G2VY-b)
Ra
375MPa
:=
Ea
210GPa
:=
n
Ea
Eb
5.385
=
:=
h
1.0m
:=
b
2.0m
:=
a
25mm
10mm
+
0.5 32
⋅
mm
+
0.051 m
=
:=
otulina
−
h1
h
a
−
0.949 m
=
:=
t
0.23m
:=
Szerokość współpracująca:
l
1.5 2.0
⋅
m
3 m
=
:=
szeroko
ść
współpracuj
ą
ca
wysi
ę
g wspornika
b1
2.0m
:=
t
h
0.23
=
b
l
0.667
=
b1
l
0.667
=
λ1
0.35
:=
l
0.8 5.45
⋅
m
:=
szeroko
ść
współpracuj
ą
ca
b2
0.5 3.05
⋅
m
1.525 m
=
:=
połowa rozpi
ę
to
ś
ci mi
ę
dzy prz
ę
słami w
ś
wietle
t
h
0.23
=
b
l
0.459
=
b2
l
0.35
=
λ2
0.66
:=
bm
λ1 b1
⋅
λ2 b2
⋅
+
b
+
3.707 m
=
:=
4.2. Obliczenie przekroju przęsłowego B-B
wg oblicze
ń
z pdfa: przekrój przesłowy1.pdf i przekrój przesłowy2.pdf
4.3. Obliczenie przekroju podporowego C-C
wg oblicze
ń
z pdfa: przekrój podporowy.pdf
6. Wymiarowanie zbrojenia poprzecznego:
Maksymalna siła poprzeczna:
V
Tc
2.635
10
3
×
kN
⋅
=
:=
τR
τb
<
τbmax
<
τR
0.40MPa
:=
:=
τbmax
4.75MPa
:=
dla B50 wg tabl 15
z
0.85 h1
⋅
0.807 m
=
:=
τb
V
b z
⋅
1.633 MPa
⋅
=
:=
τR
τb
<
τbmax
<
0.38MPa
1.688MPa
<
4.75MPa
<
Przekrój należy zbroić na ścinanie
PRZEKRÓJ-A
Siła poprzeczna:
Va
Ta
2.559
10
3
×
kN
⋅
=
:=
Nośność betonu na ścinanie:
AaL
0.04024m
2
:=
pole przekroju zbrojenia podłużnego
μ
AaL
b h1
⋅
0.021
=
:=
Mo
0
:=
Mmax
8374
:=
Siła poprzeczna przenoszona przez beton:
∆Vb
τR 1
50 μ
⋅
+
(
)
⋅
b
⋅
z
⋅
1
Mo
Mmax
+
⋅
1.329
10
3
×
kN
⋅
=
:=
Siła poprzeczna przenoszona przez strzemiona( conajmniej 50% siły poprzecznej
muszą przenieść strzemiona):
∆Vs
Va
∆Vb
−
1.23
10
3
×
kN
⋅
=
:=
∆Vs
0.5Va
<
Przyjęto strzemiona sześciotocięte ϕ10mm ze stali A-IIIN:
ϕ
10mm
:=
Raw
375MPa
:=
Faw
6ϕ
2
π
⋅
4
4.712
10
4
−
×
m
2
=
:=
Wyznaczenie rozstawu strzemion:
s
Faw Raw
⋅
z
⋅
0.5 Va
⋅
0.111 m
=
:=
smax
0.7 h1
⋅
0.664 m
=
:=
smax
300
:=
Przyjęto s=110mm
smax
80mm
150mm
−
:=
strefa podporowa
Siła poprzeczna:
V0.8a
Va 0.8
⋅
2.047
10
3
×
kN
⋅
=
:=
Siła poprzeczna przenoszona przez strzemiona( conajmniej 50% siły poprzecznej
muszą przenieść strzemiona):
−
⋅
=
:=
∆Vs
V0.8a ∆Vb
−
718.092 kN
⋅
=
:=
∆Vs
0.5V0.8a
<
Wyznaczenie rozstawu strzemion:
s
Faw Raw
⋅
z
⋅
0.5 V0.8a
⋅
0.139 m
=
:=
Przyjęto s=140mm
V0.6a
Va 0.6
⋅
1.536
10
3
×
kN
⋅
=
:=
Siła poprzeczna:
Siła poprzeczna przenoszona przez strzemiona( conajmniej 50% siły poprzecznej
muszą przenieść strzemiona):
∆Vs
V0.6a ∆Vb
−
206.219 kN
⋅
=
:=
∆Vs
0.5V0.6a
<
Wyznaczenie rozstawu strzemion:
s
Faw Raw
⋅
z
⋅
0.5 V0.6a
⋅
0.186 m
=
:=
Przyjęto s=185mm
Przyjęto s=300mm - z warunku konstrukcyjnego na pozostałej części dźwigara
PRZEKRÓJ-C
Siła poprzeczna:
Vc
Tc
2.635
10
3
×
kN
⋅
=
:=
Nośność betonu na ścinanie:
AaL
0.04024m
2
:=
pole przekroju zbrojenia podłużnego
μ
AaL
b h1
⋅
0.021
=
:=
Mo
0
:=
Mmax
8374
:=
Siła poprzeczna przenoszona przez beton:
∆Vb
τR 1
50 μ
⋅
+
(
)
⋅
b
⋅
z
⋅
1
Mo
Mmax
+
⋅
1.329
10
3
×
kN
⋅
=
:=
Siła poprzeczna przenoszona przez strzemiona( conajmniej 50% siły poprzecznej
muszą przenieść strzemiona):
∆Vs
Vc
∆Vb
−
1.306
10
3
×
kN
⋅
=
:=
∆Vs
0.5Vc
<
Przyjęto strzemiona sześciocięte ϕ10mm ze stali A-IIIN:
ϕ
10mm
:=
Raw
375MPa
:=
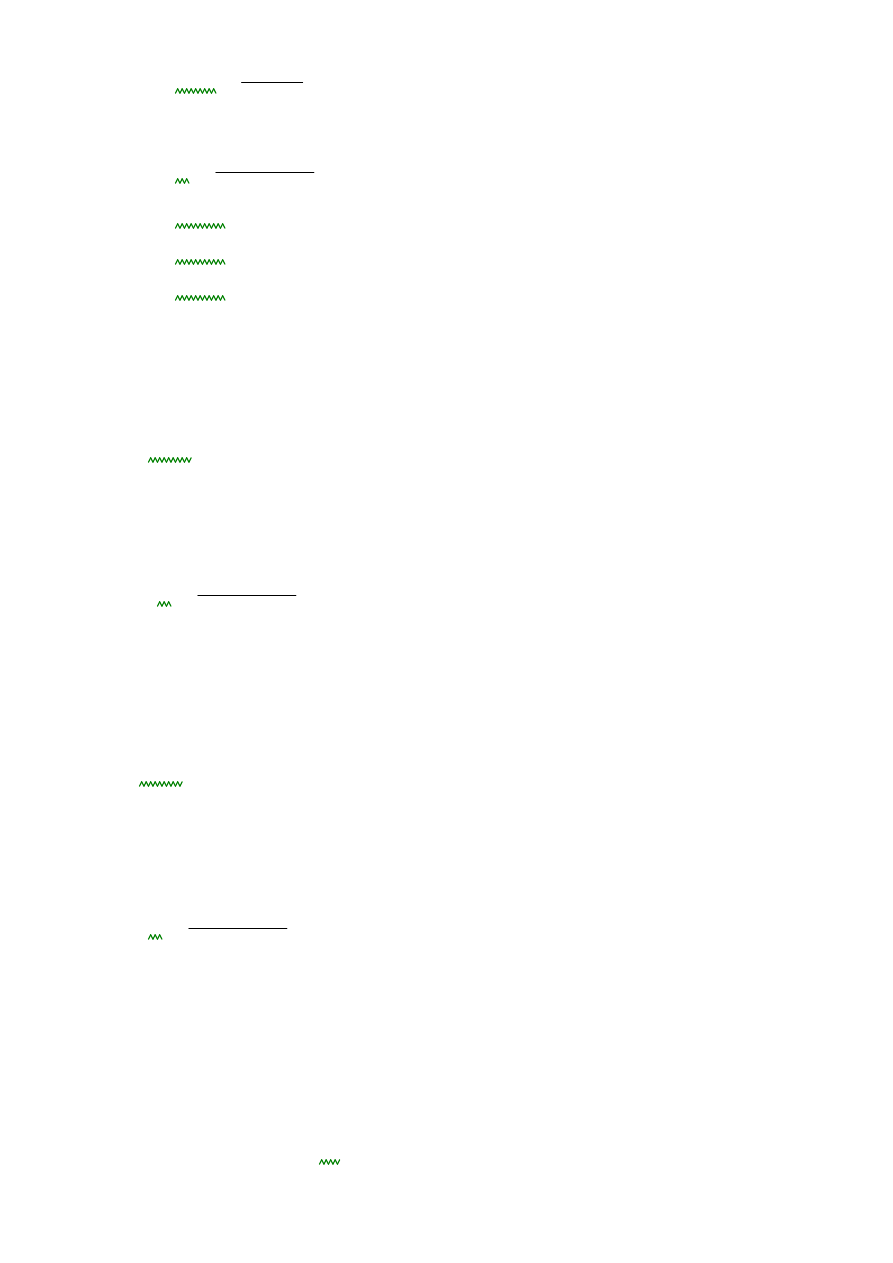
Faw
6ϕ
2
π
⋅
4
4.712
10
4
−
×
m
2
=
:=
Wyznaczenie rozstawu strzemion:
s
Faw Raw
⋅
z
⋅
0.5 Vc
⋅
0.108 m
=
:=
smax
0.7 h1
⋅
0.664 m
=
:=
smax
300
:=
Przyjęto s=105mm
smax
80mm
150mm
−
:=
strefa podporowa
Siła poprzeczna:
V0.8c
Vc 0.8
⋅
2.108
10
3
×
kN
⋅
=
:=
Siła poprzeczna przenoszona przez strzemiona( conajmniej 50% siły poprzecznej
muszą przenieść strzemiona):
∆Vs
V0.8c ∆Vb
−
778.783 kN
⋅
=
:=
∆Vs
0.5V0.8c
<
Wyznaczenie rozstawu strzemion:
s
Faw Raw
⋅
z
⋅
0.5 V0.8c
⋅
0.135 m
=
:=
Przyjęto s=135mm
V0.6c
Vc 0.6
⋅
1.581
10
3
×
kN
⋅
=
:=
Siła poprzeczna:
Siła poprzeczna przenoszona przez strzemiona( conajmniej 50% siły poprzecznej
muszą przenieść strzemiona):
∆Vs
V0.6c ∆Vb
−
251.737 kN
⋅
=
:=
∆Vs
0.5V0.6c
<
Wyznaczenie rozstawu strzemion:
s
Faw Raw
⋅
z
⋅
0.5 V0.6c
⋅
0.18 m
=
:=
Przyjęto s=180mm
Przyjęto s=300mm - z warunku konstrukcyjnego na pozostałej części dźwigara
7. Stan graniczny rozwarcia rys:
Wysokość strefy współpracującej betonu ze stalą:
x
0.217m
:=
ϕ
32mm
:=
a
0.051 m
=
heff
h
x
−
0.783 m
=
:=
:=
heff
200mm
:=
heff
a
ϕ
+
20mm
+
7.5ϕ
+
0.343 m
=
:=
Przyjęto min:
heff
200mm
:=
Średni rozstaw rys
s
65mm
:=
rozstaw prętów podłużnych
χ
1
0.5
heff
h
x
−
⋅
−
0.872
=
:=
sR
1.27 χ
⋅
s
⋅
60mm
+
0.132 m
=
:=
Dopuszczalne rozwarcie rys
wk
0.2mm
:=
Naprężenia zastępcze:
σared
wk Ea
⋅
sR
318.164 MPa
⋅
=
:=
Maksymalny moment zginający od obciążeń charakterystycznych w przęśle:
Mbk
gk
∆gk
+
(
) F1
F2
+
(
)
qzk
qztk
+
(
) F1
( )
⋅
+
Kzk η1
η2
+
η3
+
η4
+
(
)
⋅
+
:=
Mbk
5.55
10
3
×
kN m
⋅
⋅
=
Naprężenia maksymalne:
Aa
AaL
0.04 m
2
=
:=
σamax
Mbk
Aa h1
x
3
−
⋅
157.312 MPa
⋅
=
:=
σamax
σared
<
Warunek spełniony
8. Sprawdzenie ugięć:
Ugięcie dopuszczalne od obc. ruchomych dla mostu drogowego:
L
17m
:=
f
L
600
28.333 mm
⋅
=
:=
Maksymalny moment charakterystyczny od obciążeń ruchomych:
Mmax
qzk
qztk
+
(
)F1
Kzk η1
η2
+
η3
+
η4
+
(
)
⋅
+
2.88
10
3
×
kN m
⋅
⋅
=
:=
Ugięcie od obc. charakterystycznych ruchomych
kf
1.56
:=
wg tabl. 18 dla ρ
ρ
Aa
b h
⋅
0.02
=
:=
stopie
ń
zbrojenia
Ib
b h
3
⋅
12
0.167 m
4
=
:=
fp
5
48
Mmax L
2
⋅
Eb Ib
⋅
⋅
kf
⋅
20.811 mm
⋅
=
:=
fp
f
<
Warunek spełniony