03 stykowe multisim

POLITECHNIKA RADOMSKA

WYDZIAŁ TRANSPORTU I ELEKTROTECHNIKI

LABORATORIUM

Podstaw Techniki Cyfrowej

Ćwiczenie 3

Temat: Realizacja układów kombinacyjnych na

elementach stykowych

POLITECHNIKA RADOMSKA

WYDZIAŁ TRANSPORTU I ELEKTROTECHNIKI

1. Cel ćwiczenia

Celem ćwiczenia jest wykonanie projektu układu kombinacyjnego zrealizowanego w oparciu o elementy przełączające, jakimi są zestyki np. przekaźników, ze szczególnym uwzględnieniem minimalizacji funkcji logicznych za pomocą metody tablic Karnaugha.

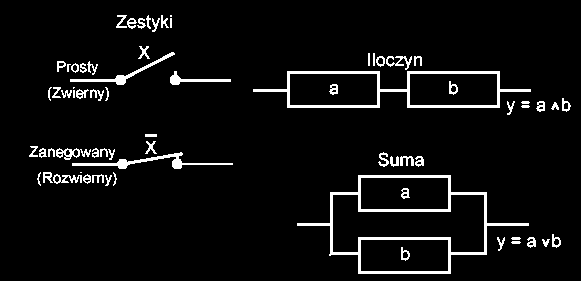
2. Założenia dotyczące realizacji układów elektrycznych na zestykach (przełącznikach)

1 – istnieje droga dla prądu (obwód elektryczny zamyka się

od „+” do „-” zasilania (np. 24V)

0 – brak drogi dla prądu

3. Zasady minimalizacji funkcji.

1. Tablica Karnaugha zawiera 2n pól opisanych kolejnymi słowami kodu Graya. Opis ten jest charakterystyczną właściwością tabeli, wykorzystywaną do przeprowadzenia uproszczeń w oparciu o regułę sklejania.

A•x + A•x = A

(B + x) • (B + x) = B

gdzie: A i B są zmiennymi logicznymi.

Wynika stąd, że zmienną, która w dwóch sąsiednich polach przyjmuje różne wartości można pominąć. Liczbę 2n pól (kratek tablicy) uzyskujemy dzieląc zbiór elementów wejściowych funkcji Z=(x0, x1, .... xn) na dwa podzbiory: Z1=(x0, x1, .... xk-1) oraz Z2=(xk, xk+1,.... xn) przyporządkowujące pierwszemu z nich kolumny tabeli, a drugiemu wiersze. Tak określona tabela zawiera 2k kolumn oraz 2n-k wierszy. Wygodnie jest dzielić zbiór Z w taki sposób, aby k=n/2, czyli uzyskiwać tabelę zbliżoną do kwadratu.

2. W tabelę przygotowaną wg punktu 1 wpisujemy wartości funkcji. W pola odpowiadające kombinacjom zmiennych, dla których wartość funkcji jest nieokreślona wpisujemy umowny znak nieokreśloności np. „-”.

3. Łączymy możliwie największe obszary obejmujące wyłącznie jedynki (dla postaci alternatywnej) lub wyłącznie zera (dla postaci koniunkcyjnej) sąsiadujące ze sobą.

Rysowanie obwiedni tych obszarów odbywa się według następujących zasad: a) Liczba pól elementarnych połączonych ze sobą musi być potęgą dwójki (1, 2, 4, 8, 16 itd.).

b) Łączone pola muszą mieć kształt symetryczny względem osi symetrii tabeli (kwadraty lub prostokąty).

c) Wszystkie jedynki lub wszystkie zera muszą być pokryte połączeniami.

POLITECHNIKA RADOMSKA

WYDZIAŁ TRANSPORTU I ELEKTROTECHNIKI

Jeżeli w tabeli występuje znak nieokreśloności to pola elementarne, w których występuje ten znak można łączyć z jedynkami lub zerami zachowując zasady łączenia przedstawione wyżej.

4. Każdemu obszarowi z jedynkami odpowiada iloczyn elementarny, którego czynniki stanowią pojedyncze zmienne wejściowe, a więc po pokryciu obszarami łączeń wszystkich jedynek wypisujemy funkcję w postaci sumy iloczynów. Analogicznie przez pokrycie wszystkich zer otrzymujemy funkcję w postaci iloczynu sum elementarnych.

4. Przykład

Przedstaw realizację funkcji logicznej F = Σ [3,4,6,7,15 (0,5,11)] w postaci układu elektrycznego wykonanego na elementach stykowych.

Liczby w nawiasach oznaczają stany nieokreślone.

1. Zapisujemy wyróżnione liczby w kodzie binarnym

0 0 0 0

0 0 1 1

0 1 0 0

0 1 0 1

0 1 1 0

0 1 1 1

1 0 1 1

1 1 1 1

2. Budujemy tablicę Karnaugha (zgodnie z zasadami przedstawionymi w pkt. 3)

a2a1

a4a3

3. Minimalizujemy funkcję

F = ā4 a3 + a2 a1

4. Rysujemy schemat połączeń wykorzystując zestyki przekaźników (i założenia z pkt.1) ā

4 a3

+24V

2 a1

POLITECHNIKA RADOMSKA

WYDZIAŁ TRANSPORTU I ELEKTROTECHNIKI

5. Przebieg ćwiczenia

W czasie zajęć laboratoryjnych należy połączyć układ będący rozwiązaniem uprzednio podanego zadania i sprawdzić poprawność jego działania (zgodność działania układu z założeniami zadania i sugestiami prowadzącego zajęcia).

6. Przykłady do samodzielnej realizacji

1) F = ∑ [0,1,3,7,9,10 (11,13,15)]

8) F = ∑ [7,9,11,13 (0,1,15)]

2) F = ∑ [1,2,3,7,10,11 (4,14)]

9) F = ∑ [1,3,5,10,11,12,13,14,15 (0,4)]

3) F = ∑ [2,3,10,11,15 (4,7,12)]

10) F = ∑ [2,3,5,6,7,11 (4,10,13)]

4) F = ∑ [4,5,6,7,10,11 (9)]

11) F = ∑ [2,3,4 (1,5,6,7,11)]

5) F = ∑ [0,1,2,6,10,15 (7,14)]

12) 7) F = ∑ [2,3,5,7,10,14,15 (8,11)]

6) F = ∑ [3,4,6,7,15 (0,5,11)]

13) F = ∑ [0,2,4,5,6,7 (3,8)]

7) F = ∑ [2,5,7,10,14 (6,9,15)]

14) F = ∑ [1,3,5,9,11,13,15 (4,7,12)]

7. Literatura

1. Cegłowski L., Goryca Z., Lewiński A.: Laboratorium układów cyfrowych. Wydawnictwo WSI w Radomiu, Radom 1987.

2. Kruszyński H., Rydzewski A., Śluzek A.: Teoria układów cyfrowych. WPW, Warszawa 1987.

3. Misiurewicz P.: Podstawy techniki cyfrow ej. WNT, Warszawa 1982.

4. Misiurewicz P.: Układy automatyki cyfrowej. WSiP, Warszawa 1984.

5. Majewski W.: Układy logiczne. WNT, Warszawa 1976.

6. Noga K., Radwański M.: Technika cyfrowa. Multisim w przykładach. BTC, Legionowo 2009

7. Perkowski M., Rydzewski A., Misiurewicz P.: Teoria układów logicznych. WPW, Warszawa 1977.

8. Traczyk W.: Układy cyfrowe - podstawy teoretyczne i metody syntezy. WNT, Warszawa 1982.