3. Zaprojektować układ sekwencyjny przechodzący kolejno przez podane stany: 0,1,2,5,6,3,0,....
a) używając przerzutnika T.
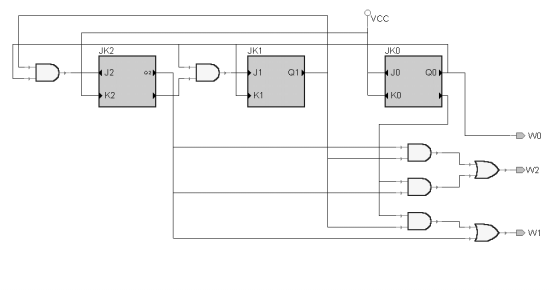
b) używając przerzutnika JK
c) używając przerzutnika D
S0
S1
S2
/0
/1
/2
S5
S4
S3
/3
/6
/5
S0 ! 000
S1 ! 001
S2 ! 010
S3 ! 011
S4 ! 100
S5 ! 101
S
S*
WY
S0
S1
0
S1
S2
1
S2
S3
2
S3
S4
5
S4
S5
6
S5
S0
3
Tablica pobudzeń dla JK
Q
Q*
J
K
0
0
0
X
0
1
1
X
1
0
X
1
1
1
X
0
W2
W1
W0 Q2 Q1 Q0 Q2* Q1* Q0* J2 K2 J1 K1 J0 K0 T2 T1 T0 D2 D1 D0
0
0
0
0
0
0
0
0
1
0
X
0
X
1
X
0
0
1
0
0
1
0
0
1
0
0
1
0
1
0
0
X
1
X
X
1
0
1
1
0
1
0
0
1
0
0
1
0
0
1
1
0
X
X
0
1
X
0
0
1
0
1
1
1
0
1
0
1
1
1
0
0
1
X
X
1
X
1
1
1
1
1
0
0
1
1
0
1
0
0
1
0
1
X
0
0
X
1
X
0
0
1
1
0
1
0
1
1
1
0
1
0
0
0
X
1
0
X
X
1
1
0
1
0
0
0
X
X
X
1
1
0
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
1
1
1
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
0 0 X 1
0 1 X 0
W2=Q0Q1+Q’0Q2
0 1 X 1
0 0 X 1
W1=Q’0Q1+Q2
0 0 X 0
1 1 X 1
W0=Q0
Pobudzenia dla JK
Q0\Q2Q1
0 0 X X
X X X X
0 1 X X
X X X 1
J2=Q0Q1
K2=1
0 X X 0
X 0 X X
1 X X 0
X 1 X X
J1=Q0Q’2
K1=Q0
1 1 X 1
X X X X
X X X X
1 1 X 1
J0=1
K0=1
Pobudzenia dla T
0 0 X 0
0 0 X 0
1 1 X 1
0 1 X 1
1 1 X 0
1 1 X 1
T2=Q0Q1+Q0Q2
T1=Q0Q’2
T0=1
Pobudzenia dla D
0 0 X 1
0 1 X 0
1 1 X 1
0 1 X 0
1 0 X 0
0 0 X 0
D
D
2=Q0Q1+Q’0Q2
1=Q’0Q1+Q0Q’1Q’2
D0=Q’0
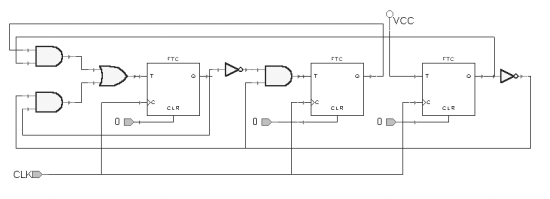
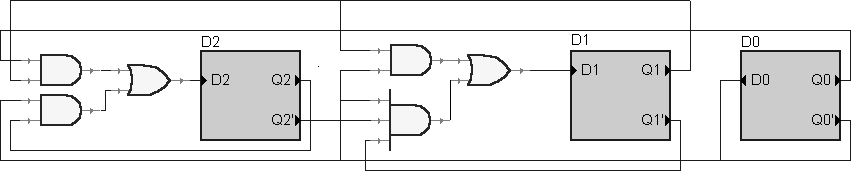
Następne schematy nie posiadają zaznaczonych wyjść (które są takie same dla wszystkich przypadków) b)
c)
Wyszukiwarka
Podobne podstrony:
cwiczenia synchroniczne, uklsek cw2
cwiczenia, synchroniczne uklsek-cw3
cwiczenia synchroniczne, uklsek cw1
cwiczenia, synchroniczne uklsek-cw1
cwiczenia synchroniczne, uklsek cw4
Cw2, Ćwiczenia 17
V semestr, cwiczenie koncowe - Piotr Zając, TEMAT: Silniki synchroniczne
V semestr, cwiczenie koncowe - Piotr Zając, TEMAT: Silniki synchroniczne
MSI cwiczenia Cw2
Przebiegi ćwiczeń, PiU ćw2
Ćwiczenie S1 Prądnica synchroniczna Pomiary parametrów i praca samotna, s1 f
cw2 okladka, Geodezja, Geodezja Inżynieryjna, gin cwiczenia
Ćwiczenie S1, Prądnica synchroniczna. Pomiary parametrów i praca samotna s1 f
SYNTEZA ĆW2, Ćwiczenia
cw2 Golabek, Ćwiczenia - dr Gołąbek
Ćwiczenia, Instrukcja do ćwiczenia 4, Układy sekwencyjne - przerzutniki asynchroniczne i synchronicz
lz-cw2, Logistyka, rok2, logistyka zaopatrzenia, cwiczenia, lz-cw2, lz-cw2
Celem ćwiczenia jest zaprojektowanie własnego układu synchronicznego realizującego taką funkcjęx
Ped społ ćw2, Materiały szkolne, ćwiczenia
więcej podobnych podstron