26.10.2012

Ćwiczenia 2

1. Przepływ fizyczny - jest w przeciwnym kierunku niż przepływ informacyjny. Przepływ informacyjny płynie z rynku.

• Klienci często strzegą informacji

• Informacje o wielkości potrzeb - popyt niezależny (potem przerodzi się w popyt rzeczywisty)

• Popyt zależny - jak już określimy wielkość produkcji

• Dobry biznes wymaga dobrej znajomości tego, co oczekuje rynek

Prognozowanie: - ważny proces biznesowy - wielość metod
Stan istniejący
- niewielka ilość lub brak danych ilościowych - zależność pomiędzy zdarzeniami w przeszłości i przyszłymi nie da się modelować ilościowo lub jest to bardzo trudne	- duża dostępność - dowiedziony związek pomiędzy zmienną zależną a zmiennymi niezależnymi
	Metody ilościowe
Techniki jakościowe: - badanie rynku - prognozy nastrajające - metoda analogii cyklu życia - dyskusje panelowe - metoda delficka	Zmienna zależna określona jest w funkcji czasu Modele oparte na szeregach czasowych	Zmienna zależna określona jest w funkcji innego parametru niż czasu Modle przyczynowo-skutkowe

2. Zmienne:

• Zależne

• Niezależne

• Przykłady:

• Np. popyt na kredyty - zmienne:

• Stopa procentowa

• Dochody gospodarstw domowych

• Wielkość kar za nieterminową spłatę

• Np. szacowanie liczby wypadków w funkcji liczby zarejestrowanych samochodów

Modele prognozowania oparte na szeregach czasowych:

• Wykorzystanie analizy szeregów czasowych w celu opracowania prognozy

• Istotna jest wartość obserwacji, jak również ich uporządkowanie chronologiczne

• Szereg czasowy - złożony jest z obserwacji uporządkowanych w kolejności chronologicznej

• Postać tabelaryczna

• Postać graficzna (x - os czasu, y - popyt)

• Zjawiska obserwowane w szeregu czasowym:

• Losowość - nieprzewidywalne wahania wartości zmiennej z okresu na okres

• Trend - długookresowy wzrost lub spadek wartości w szeregu czasowym

• Sezonowość - powtarzalny schemat wzrostów i spadków związany z konkretnymi okresami

• Przykład - zapotrzebowanie na energie w Polsce

• Rodzaje modeli:

• Metoda naiwna

• Średnia ruchoma

• Średnia ruchoma warzona

• Wygładzanie wykładnicze

• Regresja liniowa

• Metoda naiwna:

• Najprostsza metoda prognozowania oparta na szeregach czasowych

• Prognoza potrzeb F_(t+1)

• 
  

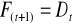
• F_(t+1) - prognoza potrzeb dla następnego okresu (t+1)

• D_t - popyt w bieżącym okresie t

• Średnia ruchoma:

• Metoda wykorzystująca znajomość wartości średniej kilku ostatnich obserwacji

• Prognoza potrzeb F_(t+1)

• 
  

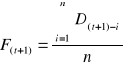
• F_(t+1) - prognoza potrzeb dla następnego okresu (t+1)

• D_(t+1)-i - rzeczywisty popyt w bieżącym okresie

• n - liczba najnowszych obserwacji wykorzystywanych przy sporządzaniu prognozy

• Średnia ruchoma warzona:

• Jest to odmiana metody średniej ruchomej

• Polega na przypisywaniu wag obserwacjom z poprzednich okresów

• Przyjęte wagi mogą się od siebie różnic

• Prognoza potrzeb F_(t+1)

• 
  

• 
  

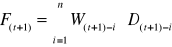
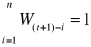
• W_(t+1)-i - waga przypisana popytowi okresu (t+1)-i

• Znaczenia pozostałych symboli podano uprzednio

• Model wygładzania wykładniczego (Model Browna - Simple Brown):

• Szczególna forma metody średniej ruchomej

• Prognoza F_(t+1) na następny okres obliczana jest jako średnia ważona wartości rzeczywistej i prognozy dla okresu bieżącego:

• 
  

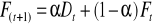
• F_(t+1) - prognoza dla okresu (t+1), najnowsza prognoza

• F_t - prognoza dla okresu t (bieżąca prognoza)

• D_t - rzeczywista wartość popytu dla okresu t

• α - stała wykładnicza użyta do warzenia D_t i F_t, 0 ≤ α ≤ 1

• W najnowszej prognozie F(t+1) są uwzględnione wszystkie wartości rzeczywiste, począwszy od pierwszego okresu

• Liniowy model wygładzania wykładniczego Holta:

• Daje możliwość prognozowania w przypadku, gdy w szeregu czasowym wystąpi trend malejący albo rosnący (otrzymuje się prognozę nieopóźnioną)

• Model Holta opiera się na modelu wygładzania wykładniczego i uwzględnia współczynnik dostosowania o trendu

• Prognoza potrzeb AF_(t+1)

• 
  

• 
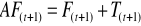
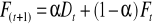
  - prognoza według modelu wygładzania wykładniczego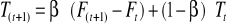

• 
  

• T_(t+1) - współczynnik trendu dla następującego okresu

• T_t - współczynnik trendu dla bieżącego okresu

• β - stała wygładzania dla współczynnika dostosowania do trendu

• Regresja liniowa:

• Technika statystyczna pozwalająca wyrazić prognozowaną zmienną jako funkcje liniowa określonej zmiennej niezależnej

• W przypadku modelu szeregu czasowego zmienną niezależną jest czas

• Prognoza potrzeb ŷ:

• 
  

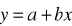
• ŷ - prognoza dla zmiennej zależnej y (potrzeby materiałowe)

• x - zmienna niezależna użyta do prognozowania potrzeb materiałowych (zmiennej zależnej y)

• â - szacowany wolny wyraz funkcji (7)

• b^ - szacowany współczynnik kierunkowy funkcji (7)

• Wartość â i b^ szacuje się na podstawie pierwotnych szeregów czasowych:

• 
  

• 
  

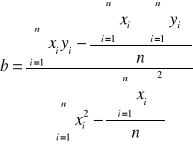
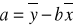
• (x_i, y_i) - przy powiązanych ze sobą obserwacjach wartości zmiennej x i y

• y^ - średnia wartość zmiennej y

• x^ - średnia wartość zmiennej x

• n - liczba par obserwacji

• Wybrane mierniki trafności prognoz:

• błąd prognozy (FE) = wartość rzeczywista - wartość prognozowana

• Średni błąd prognozy

• 
  

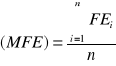
• Średnie odchylenie bezwzględne

• 
  

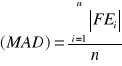
• ΣFE_i - suma błędów prognoz dla okresów 1,2,...,n

Logistyka (inżynierska)	Przedmiot: Logistyka zaopatrzenia (ćwiczenia)
Rok akademicki 2012/2013	Semestr III
Dr R. Janecki	Autor notatki: lic. Krzysztof Podgórski

1

---