statyka.com.pl
Przykład 11
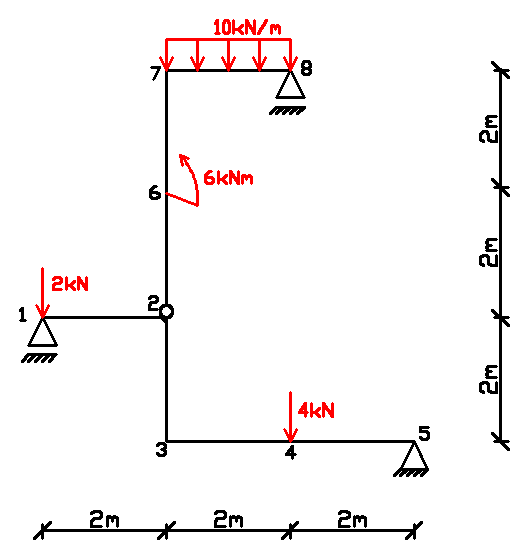
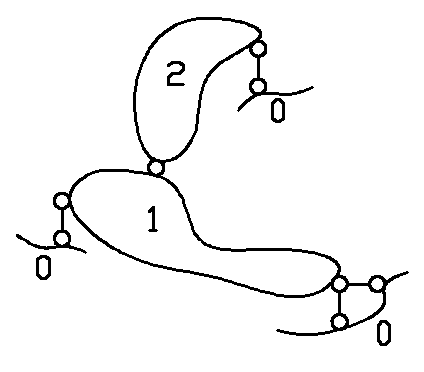
1. Statyczna wyznaczalność i geometryczna niezmienność Liczba tarcz t = 2
Liczba więzi e = 6
e = 3t
6 = 3 · 2
6=6
Układ jest statycznie wyznaczalny Tarcza 1 jest połączona z fundamentem (tarcza 0) za pomocą trzech więzi niezbieżnych i nierównoległych zatem na podstawie twierdzenia o dwóch tarczach tworzą jedną wspólna tarczę (tarcza 0). Tarcza 2 jest połączona z tarczą 0 za pomocą trzech więzi niezbieżnych i nierównoległych zatem na podstawie twierdzenia o dwóch tarczach tworzą jedna wspólną tarczę.
Układ jest geometrycznie niezmienny.
statyka.com.pl
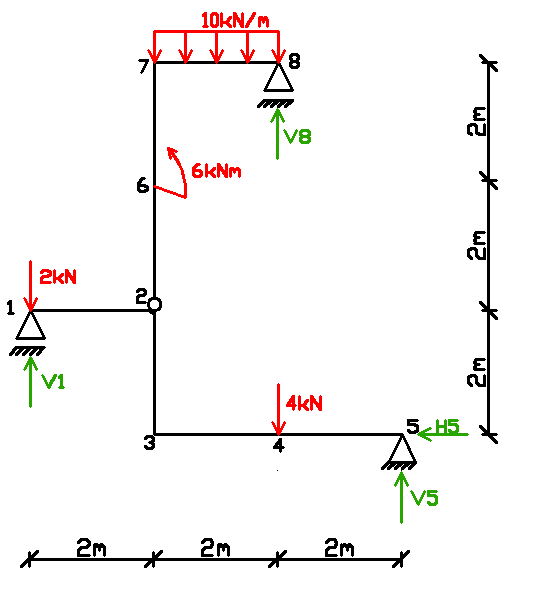
2. Wyznaczenie reakcji podpór Reakcja V8
ΣM G
2 = 0
- 6kNm + 10kN/m · 2m · 1m – V8 · 2m = 0
- 6kNm + 20kNm – V8 · 2m = 0
14kNm – V8 · 2m = 0
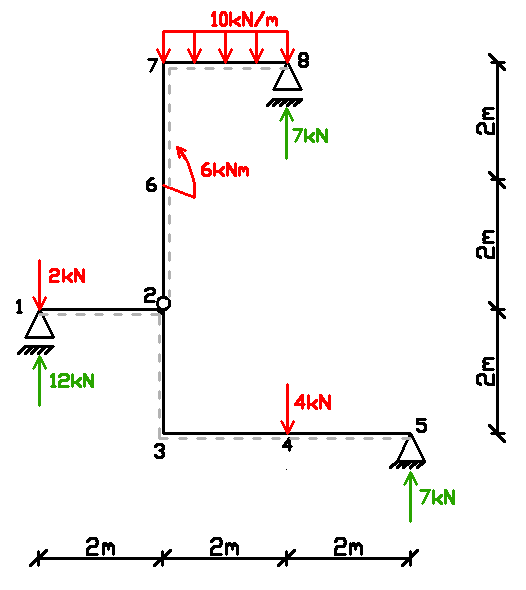
V8 = 7kN
Reakcja H5
ΣX = 0
H5 = 0
Reakcje V5 i V1
ΣY = 0
- V1 + 2kN + 4kN - V5 + 10kN/m · 2m - V8 = 0
- V1 + 2kN + 4kN - V5 + 20kN - 7kN = 0
- V1 - V5 + 19kN = 0
V1 + V5 = 19kN
statyka.com.pl
ΣM D
2 = 0
V1 · 2m – 2kN · 2m + 4kN · 2m – V5 · 4m + H5 · 2m = 0
V1 · 2m – 4kNm + 8kNm – V5 · 4m = 0
V1 · 2m – V5 · 4m = - 4kNm Otrzymujemy układ równań
V1 + V5 = 19
2 · V1 – 4 ·V5 = - 4
Po jego rozwiązaniu otrzymujemy wartości: V1 = 12kN
V5 = 7kN
Sprawdzenie
ΣM6 = 0
- V8 ·2m + 10kN/m · 2m · 1m – 6kNm – 2kN · 2m + V1 · 2m + 4kN · 2m – V5 · 4m + H5 ·4m = 0
- 7kN · 2m + 20kNm – 6kNm – 4kNm + 12kN · 2m + 4kN · 2m – 7kN · 4m = 0
-14kNm + 20kNm – 6kNm – 4kNm + 24kNm + 8kNm – 28kNm = 0
0 = 0
Reakcje policzone poprawnie
3. Siły przekrojowe
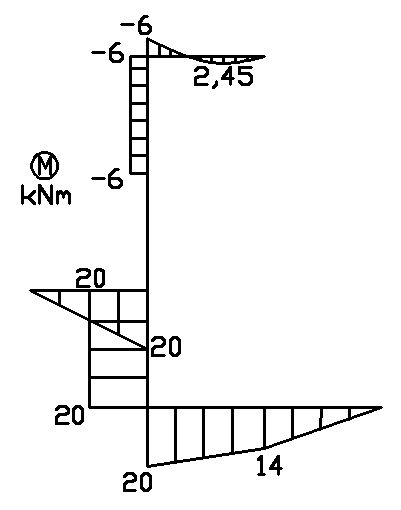
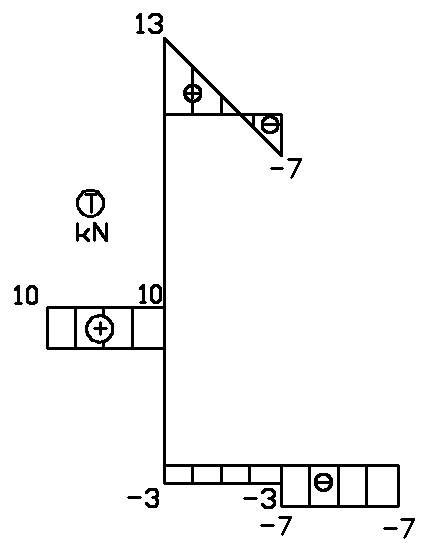
3.1 Momenty zginające
Punkt 5
M5 = 0
Punkt 4
M4 = 7kN · 2m
M4 = 14kNm
Punkt 3
M3 = 7kN · 4m – 4kN · 2m
M3 = 28kNm – 8kNm
M3 = 20kNm
Punkt 2 (od dołu)
M D
2 = 7kN · 4m – 4kN · 2m
M D
2 = 28kNm – 8kNm
M D
2 = 20kNm
Punkt 1
M1 = 0
Przedział 8 – 7, x ε [0, 2m]
M(x) = 7 · x – 10 · x · 0,5 · x M(x) = 7x - 5x2
Ekstremum
M(x) = 7x – 5x2
M'(x) = 7 – 10x
0 = 7 – 10x
x = 0,7m
M(x) = 7x – 5x2
M(0,7) = 7 · 0,7 – 5 · 0,72
M(0,7) = 4,9 – 2,45
M(0,7) = 2,45kNm
Funkcja osiąga ekstremum gdy x = 0,7m i jej wartość w tym punkcie wynosi 2,45kNm
Punkt 8, x = 0
M(x) = 7x - 5x2
M(0) = 0
Punkt 7, x = 2m
M(x) = 7x – 5x2
M(2) = 7 · 2 – 5 · 22
M(2) = 14 – 20
M(2) = - 6kNm
Punkt 6 (z góry)
M G
6 = 7kN · 2m – 10 kN/m · 2m · 1m M G
6 = 14kNm – 20kNm
M G
6 = - 6kNm
Punkt 6 (z dołu)
M D
6 = 7kN · 2m – 10 kN/m · 2m · 1m + 6kNm M D
6 = 14kNm – 20kNm + 6kNm M D
6 = 0
Punkt 2 (z góry)
M G
2 = 0
3.2 Siły tnące
Przedział 5-4
T5-4 = - 7kN
Przedział 4-3
T4-3 = -7kN + 4kN
T4-3 = -3kN
Przedział 3-2
T3-2 = 0
Przedział 1-2
T1-2 = 12kN – 2kN
T1-2 = 10kN
Przedział 2-6
T2-6 = 0
Przedział 6-7
T6-7 = 0
Przedział 8-7
M(x) = 7x – 5x2
M'(x) = 7 – 10x
T(x) = - 7 + 10x
Punkt 8, x = 0
T(x) = - 7 +10x
T(0) = - 7kN
Punkt 7, x = 2m
T(x) = - 7 +10x
T(2) = - 7 + 20
T(2) = 13kN
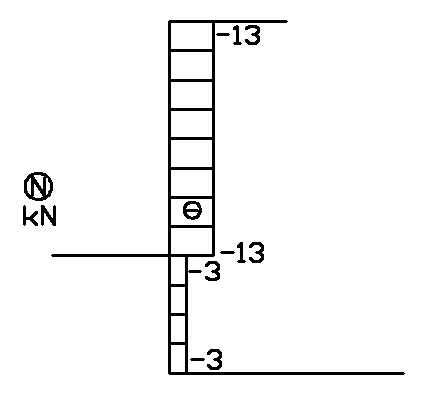
3.3 Siły osiowe
Przedział 5-4
N5-4 = 0
Przedział 4-3
N4-3 = 0
Przedział 3-2
N3-2 = - 7kN + 4kN
N3-2 = - 3kN
Przedział 1-2
N1-2 = 0
Przedział 8-7
N8-7 = 0
statyka.com.pl
Przedział 7-6
N7-6 = 7kN – 10kN/m · 2m
N7-6 = 7kN – 20kN
N7-6 = - 13kN
Przedział 6-2
N6-2 = 7kN – 10kN/m · 2m N6-2 = 7kN – 20kN
N6-2 = -13kN
4. Wykresy sił przekrojowych
statyka.com.pl