2. Dobór wymiarów fundamentu

2.1 Dobór powierzchni technologicznej

x

:=

- minimalna odległość krawędzi fundamentu od korpusu maszyny - pole kr

20cm

technologiczne

a

:=

:=

m

460cm

bm

240cm

a

:=

+

=

tech

am 2xkr 5 m

b

:=

+

=

tech

bm 2xkr 2.8m

2.2 Dobór wysokości części górnej fundamentu h :=

- grubość posadzki

s

50cm

h :=

+

=

- wysokość części górej fundamentu g

hs 10cm 0.6m

2.3 Obliczenie położenia środka ciężkości układu maszyna-część górna fundamentu Współrzędne środka ciężkości układu część górna fundamentu-maszyna Współrzędne

Oznaczenie Ciężar Q

S

i

y z=Qixi

Szx=Qixi

xi

yi

ciężarów

[kN]

[m]

[kNm]

[kNm]

1.

45

2,23

-0,15

100,35

-6,75

2.

26,4

0

0

0

0

3.

210

1,27

0

266,7

0

Σ

281,4

-

-

367,05

-6,75

G :=

:=

:=

1

45kN

G2

26.4kN

G3

210kN

ΣS

:=

⋅

:= −

⋅

:=

yz

367.05kN m

ΣSzx

6.75kN m

ΣQ

281.4kN

ΣSyz

ΣSzx

x :=

=

:=

= −

s

1.3044 m

y

0.024 m

Σ

s

Q

ΣQ

a

=

=

=

tech

5 m

btech 2.8m

hg 0.6m

3

v :=

⋅

⋅

=

⋅

- objętość części górnej fundamentu g

atech btech hg 8.4 m

kN

ρ

:=

żelbetu

25

3

m

Q :=

:=

:=

⋅ =

⋅

1

45kN

Q2

26.40kN

Q3

ρżelbetu vg 210 kN

2.4 Obliczenie wymiarów podstawy fundamentu a

:= (

+

+

⋅ =

⋅

min

103cm

20cm

130.4cm) 2

506.8 cm

b

:= (

+

+

⋅ =

⋅

min

120cm

20cm

2.4cm) 2

284.8 cm

a := 5.10m

b := 2.85m

2.5 Dobór wysokości fundamentu l

:=

śrub

140cm

h :=

+

=

f

lśrub 15cm 1.55 m

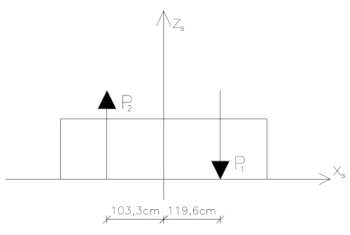
3. Ustalenie wielkości charakterystycznych sił wzbudzających 3.1 Masowe siły bezwładności w mechanizmie korbowym sprężarki P

:=

:=

z1

19.30kN

Py1

19.30kN

3.2 Siła odśrodkowa wirnika silnika G :=

⋅

=

⋅

- ciężar wirnika

w

0.35 G2 9.24 kN

P :=

⋅

=

⋅

z

0.1 Gw 0.924 kN

3.3 Wypadkowe siły wzbudzające P

:=

−

=

⋅

zo

Pz1 Pz 18.376 kN

P

:=

+

=

⋅

yo

Py1 Pz 20.224 kN

3.4 Mimośród działania sił wypadkowych P :=

=

⋅

:=

1

Pz1 19.3 kN

x1

119.6cm

P ⋅

+

⋅

1 x1

P2 x2

P :=

=

⋅

:=

:=

=

2

Pz 0.924 kN

x2

103.3cm

xp

1.1886 m

P +

1

P2

x :=

:=

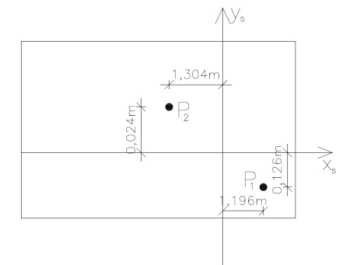
1'

1.196m

y1'

0.126m

P ⋅

−

⋅

1 y1'

P2 y2'

x :=

:=

:=

=

2'

1.304m

y2'

0.024m

yp

0.1191 m

P +

1

P2

x :=

:= −

p

1.038m

yp

0.134m

4. Wyznaczanie dopuszczalnych amplitud ω

>

[obr/min]

Maszyny tłokowe:

obr

200

obr

ω :=

ob

350 min

1

ω := 350⋅

= 5.8333⋅Hz

60s

Dopuszczalne amplitudy:

drgania poziome -

A

:=

pozioma

200μm

drgania pionowe -

A

:=

pionowa

140μm

5. Cechy sprężyste podłoża gruntowego 5.1. Dynamiczne współczynniki podłoża gruntowego 2

Wymiary podstawy fundamentu: F := a⋅b = 14.535 m

Q

:=

+

=

⋅

- ciężar maszyny

m

G1 G2 71.4 kN

Q := (

⋅

⋅ )⋅

=

⋅

g

atech btech hg ρżelbetu 210 kN

Q :=  ⋅ ⋅



( − ) ⋅

=

⋅

d

a b hf hg  ρżelbetu 345.2063 kN

- ciężar fundamentu

Q := (

+

) =

⋅

f

Qg Qd

555.2062 kN

Q

+

m

Qf

p :=

= 43.1102⋅kPa

F

b = 2.85 m

t :=

−

=

1

2.70m

1.55m

1.15 m

t :=

−

=

2

3.52m

2.70m

0.82 m

h :=

=

o

b

2.85 m

t

:= +

−

=

m

b

hf

3.52m

0.88 m

h

:= ⋅

=

o'

b

2

4.0305 m

t := ⋅

+

−

=

n

b

2

hf 3.52m 2.0605 m

 b − 0.5t

 ⋅

−



1 

b

2

0.5t1

p := ⋅

 =

⋅

:= ⋅

 =

⋅

1

p

34.4125 kPa

p

36.96 kPa



1'

p

b





b⋅ 2



b − t

( +

)

 ⋅

− ( +

)

1

0.5t2 

b

2

t1 0.5t2

p := ⋅

 =

⋅

:= ⋅

 =

⋅

2

p

19.513 kPa

p

26.4245 kPa



2'

p

b





b⋅ 2



b − t

( + +

)

 ⋅

− ( + +

)

1

t2 0.5tm 

b

2

t1 t2 0.5tn

p := ⋅

 =

⋅

:= ⋅

 =

⋅

3

p

6.6556 kPa

p

11.0196 kPa



3'

p

b





b⋅ 2



Dynamiczne współczynniki podłoża Współczynnik sprężystego równomiernego pionowego ugięcia



2⋅(a + b)

pi

gdzie "b" - bok prostopadły do kierunku w którym liczymy C

:= C ⋅ +

⋅

zi

Coi 1



i

współczynnik



∆⋅F

 po

Współczynnik sprężystego nierównomiernego pionowego ugięcia



2⋅(a + 3⋅b)

pi

C

:= C ⋅ +

⋅

φi

Co 1



o 

∆⋅F

 po

Współczynnik sprężystego równomiernego poziomego ugięcia C

:=

⋅

xi

0.70 Czi

z

Współczynnik sprężystego nierównomiernego poziomego ugięcia C

:=

⋅

ψi

1.1 Czi

z

MPa

− 1

* ) Ił półzwarty

C

:=

:=

:= ⋅

- współczynnik korygujący

o1

27

po

20kPa

∆

1 m

m



2⋅(a + b)

p1

MPa

C

:=

⋅ +

⋅

=

⋅

z1

Co1 1



74.1592



∆⋅F

 po

m



2⋅(a + 3⋅b)

p1

MPa

C

:=

⋅ +

⋅

=

⋅

φx1

Co1 1



101.9369



∆⋅F

 po

m



2⋅(3a + b)

p1

MPa

C

:=

⋅ +

⋅

=

⋅

φy1

Co1 1



123.8667



∆⋅F

 po

m

MPa

C

:=

⋅

=

⋅

x1

0.7 Cz1 51.9115 m

MPa

C

:=

⋅

=

⋅

ψ1

1.1 Cz1 81.5751 m

----------------------------------------



2⋅(a + b)

p1'

MPa

C

:=

⋅ +

⋅

=

⋅

z1'

Co1 1



76.8551



∆⋅F



po

m



2⋅(a + 3⋅b)

p1'

MPa

C

:=

⋅ +

⋅

=

⋅

φx1'

Co1 1



105.6427



∆⋅F



po

m



2⋅(3a + b)

p1'

MPa

C

:=

⋅ +

⋅

=

⋅

φy1'

Co1 1



128.3697



∆⋅F



po

m

MPa

C

:=

⋅

=

⋅

x1'

0.7 Cz1' 53.7986 m

MPa

C

:=

⋅

=

⋅

ψ1'

1.1 Cz1' 84.5407 m

MPa

* ) glina

C

:=

=

⋅

=

⋅

o2

25

p2 19.513 kPa

p2' 26.4245 kPa

m



2⋅(a + b)

p2

MPa

C

:=

⋅ +

⋅

=

⋅

z2

Co2 1



51.7065



∆⋅F

 po

m



2⋅(a + 3⋅b)

p2

MPa

C

:=

⋅ +

⋅

=

⋅

φx2

Co2 1



71.0742



∆⋅F

 po

m



2⋅(3a + b)

p2

MPa

C

:=

⋅ +

⋅

=

⋅

φy2

Co2 1



86.3645



∆⋅F

 po

m

MPa

C

:=

⋅

=

⋅

x2

0.7 Cz2 36.1946 m

MPa

C

:=

⋅

=

⋅

ψ2

1.1 Cz2 56.8772 m

----------------------------------------



2⋅(a + b)

p2'

MPa

C

:=

⋅ +

⋅

=

⋅

z2'

Co2 1



60.1709



∆⋅F



po

m



2⋅(a + 3⋅b)

p2'

MPa

C

:=

⋅ +

⋅

=

⋅

φx2'

Co2 1



82.709



∆⋅F



po

m



2⋅(3a + b)

p2'

MPa

C

:=

⋅ +

⋅

=

⋅

φy2'

Co2 1



100.5023



∆⋅F



po

m

MPa

C

:=

⋅

=

⋅

x2'

0.7 Cz2' 42.1196 m

MPa

C

:=

⋅

=

⋅

ψ2'

1.1 Cz2' 66.188 m

MPa

* ) żwir

C

:=

=

⋅

=

⋅

o3

26

p3 6.6556 kPa

p3' 11.0196 kPa

m



2⋅(a + b)

p3

MPa

C

:=

⋅ +

⋅

=

⋅

z3

Co3 1



31.4058



∆⋅F

 po

m



2⋅(a + 3⋅b)

p3

MPa

C

:=

⋅ +

⋅

=

⋅

φx3

Co3 1



43.1695



∆⋅F

 po

m



2⋅(3a + b)

p3

MPa

C

:=

⋅ +

⋅

=

⋅

φy3

Co3 1



52.4566



∆⋅F

 po

m

MPa

C

:=

⋅

=

⋅

x3

0.7 Cz3 21.9841 m

MPa

C

:=

⋅

=

⋅

ψ3

1.1 Cz3 34.5464 m

----------------------------------------



2⋅(a + b)

p3'

MPa

C

:=

⋅ +

⋅

=

⋅

z3'

Co3 1



40.4109



∆⋅F



po

m



2⋅(a + 3⋅b)

p3'

MPa

C

:=

⋅ +

⋅

=

⋅

φx3'

Co3 1



55.5476



∆⋅F



po

m



2⋅(3a + b)

p3'

MPa

C

:=

⋅ +

⋅

=

⋅

φy3'

Co3 1



67.4976



∆⋅F



po

m

MPa

C

:=

⋅

=

⋅

x3'

0.7 Cz3' 28.2876 m

MPa

C

:=

⋅

=

⋅

ψ3'

1.1 Cz3' 44.452 m

Współczynniki uśrednione b⋅ 2

MPa

C :=

=

⋅

z

50.6473

t1

t2

t

m

+

n

+

Cz1'

Cz2'

Cz3'

b

MPa

C :=

=

⋅

x

33.5937

t1

t2

t

m

+

m

+

Cx1

Cx2

Cx3

b⋅ 2

MPa

C

:=

=

⋅

φx

69.6182

t1

t2

t

m

+

n

+

Cφx1'

Cφx2'

Cφx3'

b⋅ 2

MPa

C

:=

=

⋅

φy

84.5952

t1

t2

t

m

+

n

+

Cφy1'

Cφy2'

Cφy3'

5.2. Sztywność podłoża K

3

3

a⋅b

4

a ⋅b

4

I :=

=

:=

=

x

9.8384 m

Iy

31.5046 m

12

12

MN

K :=

⋅ =

⋅

z

Cz F 736.1581 m

MN

K :=

⋅ =

⋅

x

Cx F 488.2841 m

K

:=

⋅ =

⋅

⋅

φxz

Cφx Iy 2193.2931 MN m

K

:=

⋅ =

⋅

⋅

φyz

Cφy Ix 832.2793 MN m

6. Obliczenie amplitud drgań wymuszonych fundamentu 6.1. Amplitudy drgań w płaszczyźnie XZ

+

m

Qf

Qm

g = 9.8066

ω = 5.8333⋅Hz

m :=

= 63896.0552 kg

- masa maszyny i fundamentu

2

g

s

h =

:=

f

1.55 m

zs

0.75m

h :=

s'

2.3m

ϕ := 0.0045s

ponieważ głębokość posadowienia > 1,5m i fundament jest posadowiony na gruntach w stanie naturalnej wilgotności γ := ϕ⋅ω = 0.0262

atech

a :=

=

f

2.5 m

2

*) z uwzględnieniem tłumienia drgań Kz

1

λ :=

=

- częstość drgań właśnych

z

107.3368

m

s

ω

η :=

=

=

- ramię działania siły

z

0.0543

x

λ

p

1.038 m

z

x



−

kr

hf xkr 

Q ⋅

+

⋅

+

⋅

−



m hs

Qd

Qg hf

2



2



z :=

=

k

0.4053 m

Q

+

m

Qf

K ⋅

x Kφxz

1

ω

λ :=

=

:=

=

1

85.8617

η

0.0679



1

2



s

λ

m⋅ K ⋅

+



1

x zk

Kφxz

1

v :=

=

- współczynnik dynamiczny

z

1.003



2

2

2

2

1 − η



+

⋅

z 

γ ηz

1

v :=

=

1

1.0046



2

2

2

2

1 − η



+

⋅

1 

γ η1

Pzo

Pzo

Pzo

A

:=

⋅ ⋅ ⋅

=

⋅

:=

⋅ +

⋅ ⋅ ⋅

=

⋅

H.xz

xp hf v1 13.5423 μm

AV.xz

vz

xp af v1 46.8783 μm

Kφxz

Kz

Kφxz

*) bez uwzględnienia tłumienia drgań 1

1

v :=

=

:=

=

1'

1.0046

vz'

1.003

2

2

1 − η

−

1

1

ηz

Pzo

Pzo

Pzo

A

:=

⋅ ⋅ ⋅

=

⋅

:=

⋅

+

⋅ ⋅ ⋅

=

⋅

H.xz'

xp hf v1' 13.5423 μm

AV.xz'

vz'

xp af v1' 46.8784 μm

Kφxz

Kz

Kφxz

6.2. Amplitudy drgań w płaszczyźnie YZ

6.2.1. Amplitudy drgań w płasz czyź nie YZ (siły wzbudzające pionowe)

btech

z =

=

:=

=

k

0.4053 m

m

63896.0552 kg

bf

1.4 m

2

*) z uwzględnieniem tłumienia drgań K ⋅

x Kφyz

1

λ :=

=

=

=

1

83.487

η

v



z

0.0543

z

1.003

2



s

m⋅ K ⋅

+

 x zk

Kφyz

Pyo

Pyo

Pzo

A

:=

⋅ ⋅ ⋅

= −

⋅

:=

⋅ +

⋅ ⋅ ⋅

=

⋅

H.yz

yp hf v1

1.924 μm

AV.yz

vz

xp af v1 49.3961 μm

Kφxz

Kz

Kφxz

*) bez uwzględnienia tłumienia drgań

Pyo

Pyo

Pzo

A

:=

⋅ ⋅ ⋅

= −

⋅

:=

⋅ +

⋅ ⋅ ⋅

=

⋅

H.yz'

yp hf v1

1.924 μm

AV.yz'

vz

xp af v1 49.3961 μm

Kφxz

Kz

Kφxz

6.2.1. Amplitudy drgań w płasz czyź nie YZ (siły wzbudzające pionowe)

h :=

=

s

230cm

bf

1.4 m

*) bez uwzględnienia tłumienia drgań: K ⋅

x Kφyz

1

λ :=

=

1

83.487



2



s

m⋅ K ⋅

+

 x zk

Kφyz

ω

η :=

=

1

0.0699

λ1

1

ν :=

=

1

1.0049059

2

1 − η1



K

( ⋅ ⋅ )

x hs hf 

P

⋅ +

⋅

yo 1

 v1

K



φyz



A

:=

=

⋅

oH

0.1286 mm

Kx

P

⋅ ⋅ ⋅

yo hs bf v1

A

:=

=

⋅

oV

0.0786 mm

Kφyz

*) z uwzględnieniem tłumienia drgań: 1

ν :=

=

1'

1.0049042



2

2

2

2

1 − η



+

⋅

1 

γ η1



K

( ⋅ ⋅ )

x hs hf 

P

⋅ +

⋅

yo 1

 ν1'

K



φyz



A

:=

=

⋅

oH

0.1287 mm

Kx

P

⋅ ⋅ ⋅

yo hs bf ν1'

A

:=

=

⋅

oV

0.0786 mm

Kφyz

7. Obliczenie nacisku fundamentu na podłoże gruntowe P0

q +

=

+

⋅

≤

r

qd

A0 Cz qf

F

P :=

⋅

=

⋅

- obciążenie dynamiczne dla maszyn obrotowych o prędkości obrotowej d

0.1 G2 2.64 kN do 500 obr/min; wg PN-80/B03040

qf

.

− graniczny opór jednostkowy gruntu określony zgodnie z normami obow. przy występowaniu tylko obciążeń statycznych (PN-81/B03020) qr

.

− nacisk statyczny

qd

.

− krawędziowy nacisk na podstawę A

.

− amplituda

Cz .

− współczynnik sprężystości

P ⋅

⋅ ⋅

d v

Pd v Cz

Pd

q :=

= ⋅

=

⋅ ⋅

=

⋅

d

.

ν Cz

A0 Cz

F

C ⋅

z F

Kz

Amplituda pionowa naroża dolnego fundamentu Wykorzystujemy wyniki obliczeń poprzednich w płaszczyźnie XZ

ν :=

=

z

1.0029882

v1 1.0046

Pzo

Pzo

A :=

⋅

+

⋅ ⋅

⋅

v

νz

xp 0.5a v1

Kz

Kφxz

q :=

⋅

=

d

Av Cz 2396.4192 Pa

A =

v

0 m

Wykorzystujemy wyniki obliczeń poprzednich w płaszczyźnie YZ

ν :=

=

z

1.0029882

ν1 1.0049

Pyo

A :=

⋅ ⋅

⋅

v

hs 0.5b ν1

Kφyz

A =

:=

⋅

=

v

0.0001 m

qd

Av Cz 4053.4249 Pa

Porównać amplitudy z dopuszczalnymi i wniosek