PODSTAWOWE DEFINICJE TEORII GRAFÓW
Definicja 1
Grafem skończonym G nazywamy skończony zbiór punktów V
i
, i = l, N, zwanych
wierzchołkami i skończony zbiór linii u
i
, i = l, M, zwanych krawędziami takimi, że każda
krawędź ma dwa (niekoniecznie różne) wierzchołki jako jej punkty końcowe oraz nie prze-
chodzi ona przez inne wierzchołki. Mówimy, że krawędź jest incydentna (powiązana) z
wierzchołkiem, jeśli jest on jednym z jej końców.
Definicja 2
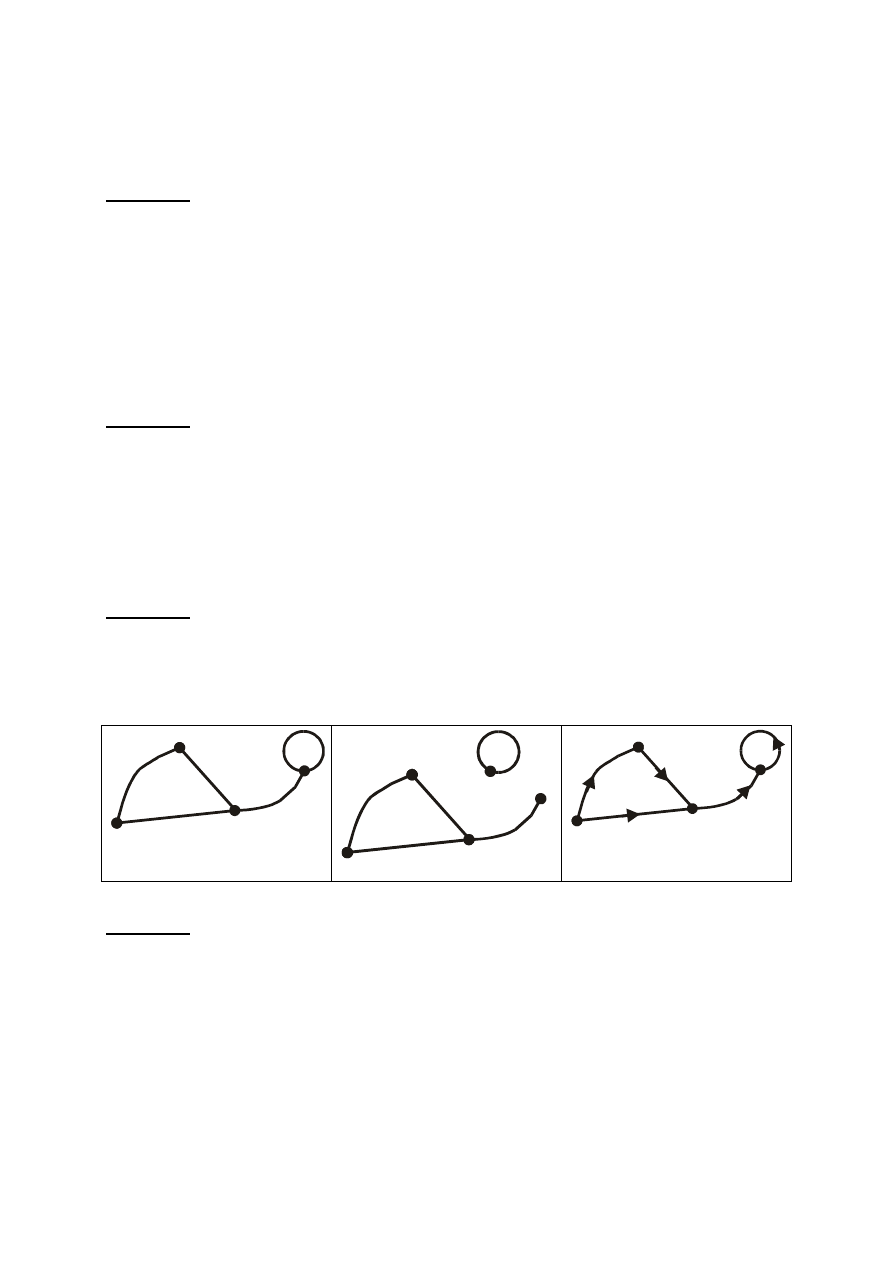
Graf G nazywamy skierowanym, jeśli każda jego krawędź ma określoną orientację.
Zorientowana krawędź „wychodzi” z wierzchołka, który jest jej początkiem i „wchodzi” do
wierzchołka, która jest jej końcem lub inaczej - jest względem obu wierzchołków dodatnio i
ujemnie incydentna.
Definicja 3
Graf G jest grafem spójnym, jeśli nie ma wierzchołków izolowanych, tzn. wierzchoł-
ków, z których nie można przejść po krawędziach grafu do dowolnego innego wierzchołka.
Na rys. 1 przedstawiono graf spójny, niespójny oraz graf spójny skierowany.
u
1
v
1
v
2
v
3
v
4
u
2
u
3
u
4
u
5
u
1
v
1
v
2
v
3
v
4
v
5
u
2
u
3
u
4
u
5
u
1
v
1
v
2
v
3
v
4
u
2
u
3
u
4
u
5
Definicja 4
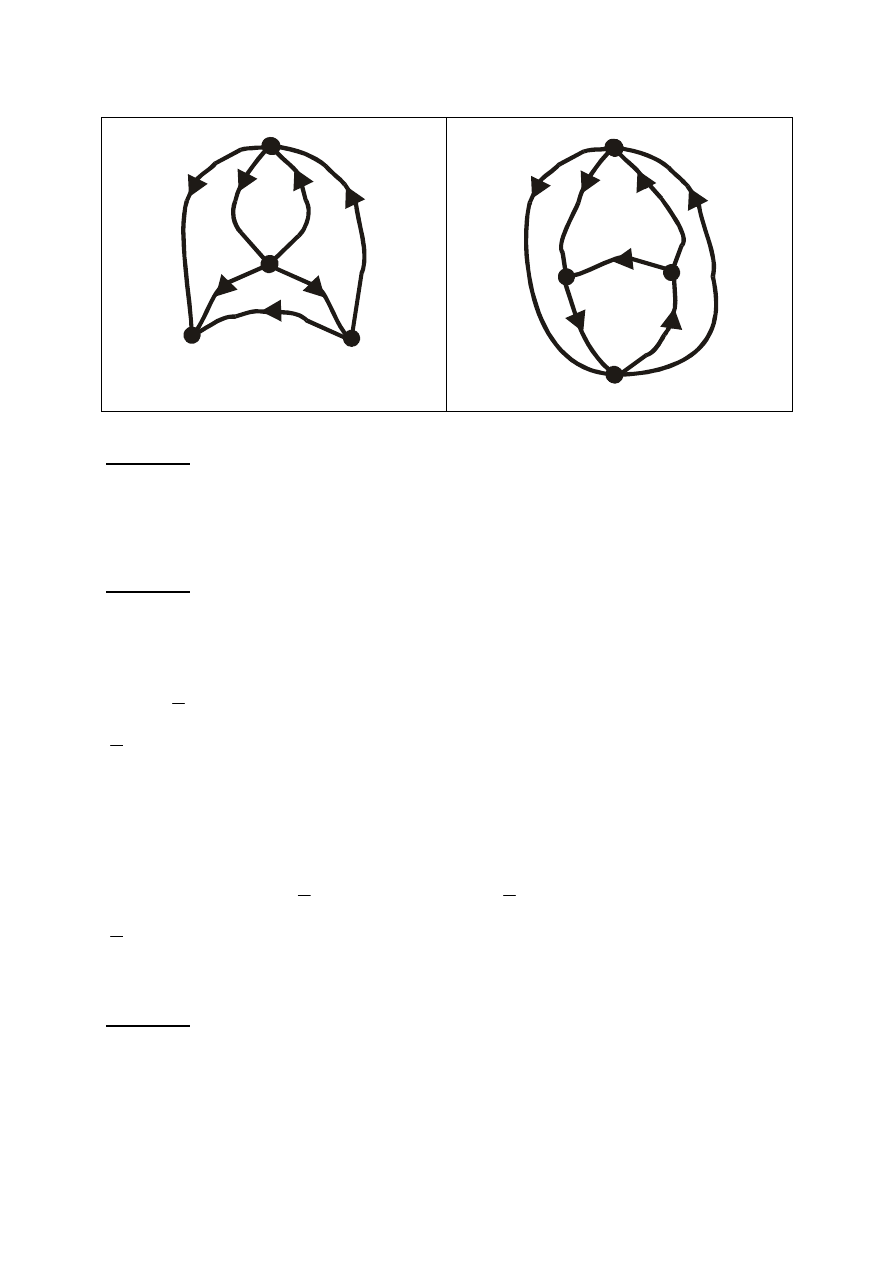
Dwa grafy są izomorficzne jeśli:
1. jest wzajemnie jednoznaczna odpowiedniość między zbiorami wierzchołków,
2. jest wzajemnie jednoznaczna odpowiedniość między ich zbiorami krawędzi,
3. zachowana jest orientacja krawędzi dla grafów zorientowanych.
v
4
v
3
v
2
v
1
u
1
u
6
u
5
u
7
u
2
u
4
u
3
v
4
v
3
v
2
v
1
u
1
u
6
u
5
u
7
u
2
u
4
u
3
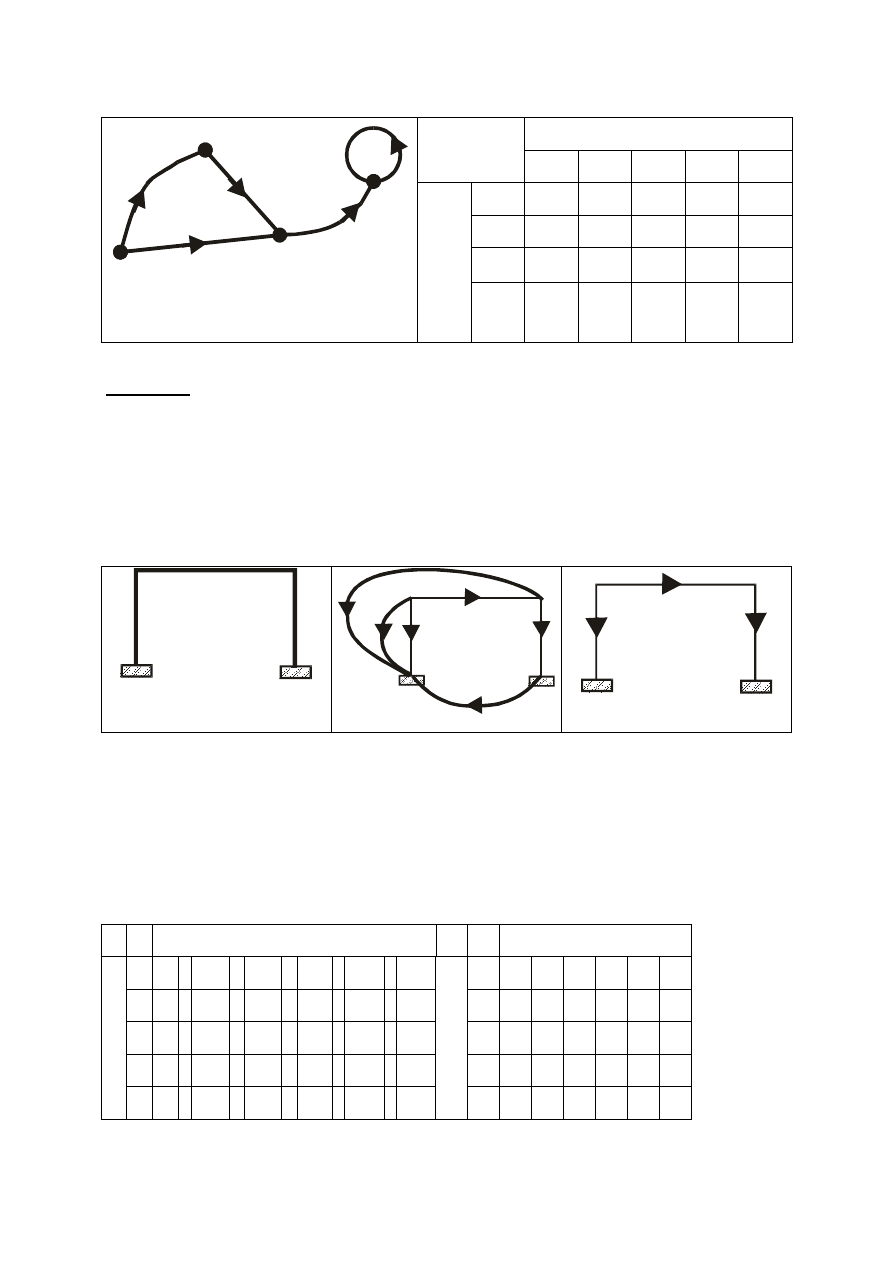
Definicja 5
Ś
cieżką nazywamy ciąg różnych krawędzi takich, że dwie kolejne krawędzie w ciągu
są incydentne względem tego samego wierzchołka.
Definicja 6
Cyklem nazywamy ścieżkę, której początkowy wierzchołek zbiega się z końcowym
wierzchołkiem pierwszej i ostatniej krawędzi.
W grafie spójnym skierowanym mającym N wierzchołków i M krawędzi, każdemu
cyklowi
j
C
przyporządkowano m - wymiarowy wektor
[
]
T
MJ
j
j
C
C
C
,...
1
, gdzie:
−
+
−
i
i
a
α
jeśli krawędź u
i
jest „przechodzona”
+
i
α
razy w kierunku
C
ij
=
zgodnym z jej orientacją oraz
−
i
α
w przeciwnym
0
jeśli u
i
nie jest częścią cyklu
Dla grafu z rys. 2 wektor
j
C
odpowiadający cyklowi
j
C
=
[
u
1
, u
2
, u
3
, u
4
, u
2
, u
6
]
T
jest równy
j
C
=
[
1, -2, -1, 1, 0 , 1, 0
]
T
.
Definicja 7
Macierz T
[
t
ij
]
wymiaru N x M nazywamy macierzą incydencji wtedy, gdy:
-1
gdy u
j
„wychodzi” do wierzchołka V
i
,
t
ij
=
+1
gdy u
j
„wychodzi” z wierzchołka V
i
,
0
gdy u
j
nie ma końca w wierzchołku V
i
.
1
1
2
3
4
2
3
4
5
k r a w ę d z i e
1
2
3
4
5
w
ę
z
ł
y
1
-1
0
1
0
0
2
1
1
0
0
0
3
0
-1
-1
1
0
4
0
0
0
-1
0
Definicja 8
Grafem planarnym nazywamy graf, którego żadna dwie krawędzie nie przecinają się z
wyjątkiem punktów końcowych.
Macierz incydencji = macierz podstawowych przekrojów grafu, zawiera informacje o
sposobie połączeń wzdłuż i prętów oraz o zwrocie prętów konstrukcji.
Np. dla ramy portalowej:
a)
b)
1
1
2
3
4
2
3
4
5
6
1
1
2
3
4
2
3
a) graf podstawowy: linie grube - krawędzie pierwszego rodzaju
linie cienkie - krawędzie drugiego rodzaju
b) graf uproszczony
Macierze incydencji są następujące:
a)
b)
p r ę t y
p r ę t y
w
ę
z
ł
y
1 2
3
4
5
6
w
ę
z
ł
y
1
2
3
1 1
1
1
1
1
1
2
-1
1
1
2
-1
1
3 -1
-1
1
3
-1
4
-1
-1 -1
4
-1
Na podstawie zdefiniowanej macierzy incydencji T określona jest uogólniona macierz
incydencji H, zwana dalej macierzą incydencji.
Elementy macierzy H ustalane są następująco:
element H(i,j) jako macierz jednostkowa:
1
s
I
dla T(i,j) = 1
-
1
s
I
dla T(i,j) = -1
o
s
I
dla T(i,j) = 0
s - wskaźnik oznaczający stopień macierzy:
s = 2 - kratownica 2D
s = 3 – rama 2D
s = 3 - kratownica 3D
s = 6 - rama 3D
Postaci macierzy I są następujące:
1
1 0
1 0 0
0 1
0 1 0
0 0 1
s=1
s=2
s=3
Ogólnie:
f
+
dla T (i,j) = 1
H(i,j) =
f
dla T (i,j) = -1
f
o
dla T (i,j) = 0
f
+
=
[
]
o
s
s
I
I ;
1
,
f
-
=
[
]
1
;
s
o
s
I
I
,
f
o
=
[
]
o
s
o
s
I
I ;
gdzie:
1
s
I
- jest macierzą jednostkową stopnia s,
o
s
I
- jest macierzą zerową stopnia s o wymiarze s x s,
gdzie s - stopień swobody węzła konstrukcji.