Zadania dla Grupy 2
1. Samochód o masie m = 1500 kg ma silnik o mocy P = 50 kW. Oś napędowa tego samochodu jest
obciążona połową ciężaru samochodu. Współczynnik tarcia f = 0.5. Obliczyć największe
przyspieszenie, z jakim może rozpoczynać jazdę ten samochód. Przy jakich prędkościach ruchu
można wywołać poślizg kół? Obliczyć długość drogi rozpędzania samochodu rozpoczynającego
jazdę z poślizgiem i czas trwania poślizgu.
Wskazówka: Samochód uzyskuje przyspieszenie dzięki sile reakcji podczas tarcia kół o podłoże –
więc a < 0.5gf. Moc silnika musi wystarczać na utrzymanie takiego przyspieszenia.
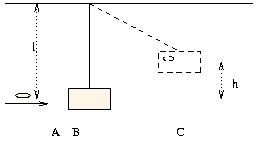
2. Piłka spada z wysokości H = 7.5 m na gładką podłogę. Jaką prędkość początkową v0 należy nadać
piłce, aby po dwóch uderzeniach o podłogę podskoczyła na wysokość pierwotną, jeśli podczas
każdego uderzenia traci 40% energii?
Wskazówka: Oblicz energię całkowitą w chwili początkowej i energie po kolejnych odbiciach.
Skorzystaj z tych zależności, by wyznaczyć prędkość.
3.
Na rysunku pokazano zsuwający się z równi pochyłej blok o masie 12
kg. Kąt nachylenia równi względem podłoża wynosi α=30o. U końca
równi zamontowano sprężynę. Stała sprężystości sprężyny
k=1.35*104N/m. Blok zatrzymuje się po ściśnięciu sprężyny o 5.5 cm.
O ile zsunął się blok z równi? Zaniedbaj tarcie. Odp. l=0.35m
Wskazówka: Skorzystaj z zasady zachowania energii.
4. Łyżwiarz stojący na gładkim lodzie rzuca kamień o masie m = 0.5 kg. Po czasie t = 2 s kamień
spada w odległości s = 20 m. Jaka jest prędkość v łyżwiarza, jeśli jego masa wynosi M = 60 kg?
(nie uwzględniać tarcia).
Wskazówka: Zastosuj zasadę zachowania pędu.
5. Na brzegu poziomej, okrągłej platformy o masie M i promieniu R stoi student o masie m.
Platforma może obracać się bez tarcia wokół pionowej osi. Jaka będzie prędkość kątowa platformy
ω, jeżeli student zacznie chodzić wzdłuż jej brzegu ze stałą względem niej prędkością v. Jaką
drogę przebędzie student względem platformy w czasie jej jednego pełnego obrotu?
Wskazówka: Korzystamy z zasady zachowania momentu pędu układu student-tarcza.
6. Ciało o masie m=1.0 kg i prędkości v=1.0 m/s zderza się czołowo z nieruchomą masą M=2.0 kg.
Jaka jest prędkość każdego z obiektów po zderzeniu, jeśli zderzenie było elastyczne? Jaka byłaby
prędkość obiektów po zderzeniu, gdyby było ono całkowicie niesprężyste? Jaka część energii
kinetycznej zostałaby rozproszona w efekcie tego zderzenia?
7. Wahadło balistyczne. Pocisk o masie mp=0.06 kg został
wystrzelony poziomo w kierunku drewnianego bloku o
masie mb=0.2 kg. Drewniany blok jest zawieszony na
lince w sposób pokazany na rysunku. Zderzenie jest
całkowicie nieelastyczne, a po zderzeniu układ blok-
pocisk unosi się na wysokość h=0.12 m względem
pozycji równowagi. Jaka była prędkość układu po
uderzeniu pocisku w blok? Jaka była prędkość pocisku
po wystrzeleniu?
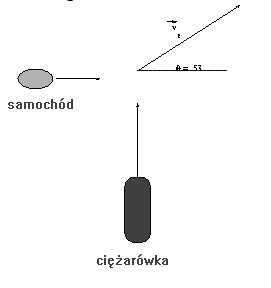
8. Samochód o masie m = 1500 kg zderza się z ciężarówką o
masie M = 2500 kg na środku skrzyżowania. Policyjny
detektyw znajduje po przybyciu oba auta szczepione i
przemieszczone na odległość d = 15 m pod kątem θ = 53o
względem kierunku wschód-zachód (rysunek). Po
przeprowadzeniu serii obliczeń, policjant ukarał kierowcę
samochodu osobowego mandatem za przekroczenie
dozwolonej prędkości (60 km/h). Czy słusznie? Z jaką
prędkością jechał ten samochód przed kolizją?
Współczynnik tarcia kinetycznego między oponami a
nawierzchnią wynosi fk = 0.8.
9. Koło zamachowe o momencie bezwładności I = 0,2 kgm2
obraca się wokół poziomej osi przechodzącej przez jego
środek, wykonując n = 600 obr/min. Przy hamowaniu
koło zatrzymuje się po upływie czasu Δt = 20 s. Znajdź moment siły hamującej i liczbę obrotów do chwili zatrzymania.
Wskazówka: Na koło działa siła tarcia, której moment hamujący M określa II zasada dynamiki dla
ruchu obrotowego. Z kolei przyspieszenie kątowe to dω /dt co można zapisać jako Δω / Δt. Wstaw odpowiednie wartości – obliczysz przyspieszenie i moment siły. Dlaczego pojawia się znak minus?
Oblicz drogę kątową i liczbę obrotów N.
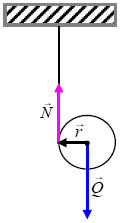
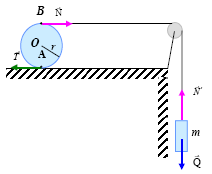
10. Na rurę o cienkich ściankach nawinięto nić, której wolny koniec przymocowano do sufitu. Rura
odkręca się z nici pod działaniem własnego ciężaru (rysunek.). Znajdź
przyspieszenie rury i siłę napięcia nici, jeżeli masę i grubość nici można zaniedbać.
Początkowa długość nici jest dużo większa od promienia rury. Ciężar rury wynosi
Q.
Wskazówka: Na rurę działają dwie siły: siła ciężkości Q i siła naprężenia nici N.
Skorzystaj z drugiej zasady dynamiki dla ruchu postępowego rury, a następnie z II zasady
ruchu obrotowego.
11. Walec o masie M i promieniu r może toczyć się po poziomym stole. Na walec nawinięta jest
nieważka i nierozciągliwa nić, którą przerzucono przez nieważki
bloczek. Na końcu nici zawieszono ciężarek o masie m (rysunek).
Wyznacz przyspieszenie ciężarka i siłę tarcia działającą na walec
przyjmując, że może być on pełen lub wydrążony (cienkościenna rura).
Wskazówki: Nieważkość nici i bloczka pozwala napisać: N = N’.
Przyspieszenie środka masy walca: aO = ε r, gdzie: ε - przyspieszenie kątowe
ruchu obrotowego, r – promień walca; przyspieszenie punktu B: aB = a = aO
+ ε r = 2 aO
Zastosuj: II zasadę dynamiki dla walca dla ruchu postępowego + II zasadę dla ruchu obrotowego,
II zasada dynamiki dla ciężarka.
Rozwiąż układ równań i wyznacz z niego przyspieszenie ciężarka a, siłę tarcia działającego na walec.
Podstaw odpowiednie wartości I.
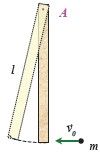
12. Belka o długości l i masie M może swobodnie obracać się wokół poziomej
osi przechodzącej przez jeden z jej końców. W drugi koniec belki uderza kula
o masie m mająca poziomą prędkość v0 (rysunek). Kula grzęźnie w belce.
Znajdź prędkość kątową belki tuż po uderzeniu kuli. W jakie miejsce belki
powinna uderzyć kula, aby składowa pozioma siły reakcji osi w chwili
uderzenia wynosiła zero?
Wskazówki: Na belkę działają dwie siły: siła ciężkości i reakcja osi. Przyjmijmy
oś A za oś odniesienia. Moment reakcji osi wynosi 0, ponieważ jej linia działania
przechodzi przez oś. Moment siły ciężkości również wynosi 0, gdyż zakładamy, iż czas hamowania kuli w belce jest bardzo krótki i belka w tym czasie nie odchyli się znacząco od pionu. Można, więc
przyjąć, że spełniona jest zasada zachowania momentu pędu. Zapisz moment pędu układu kula-belka
przed uderzeniem kuli i po uderzeniu. Skorzystaj z zasady zachowania. Oblicz prędkość kątową.
Składowa pozioma siły reakcji osi jest jedyną siłą zewnętrzną mogącą zmienić pęd układu. Jeżeli siła ta wynosi 0, to spełniona jest zasada zachowania pędu.
Przyjmijmy, że kula uderza w belkę w odległości a od osi obrotu. Wyznacz pęd układu przed zderzeniem i po. Skorzystaj z zasady zachowania momentu pędu i wyznacz p2 - pęd układu po zderzeniu. Znajdź moment bezwładności I, dla którego p1 = p2. Ponieważ tu I musi być równe Ml2/3
(pręt), to możesz wyznaczyć a. Jest to warunek spełnienia zasady zachowania pędu i wówczas składowa pozioma siły reakcji osi wynosi zero.
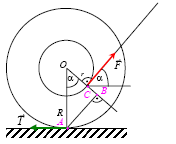
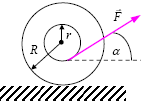
13. Kołowrót o masie m, momencie bezwładności I0 i promieniach
zewnętrznym R oraz wewnętrznym r leży na płaszczyźnie poziomej
(rysunek). Na kołowrót nawinięta jest nić, do której przyłożono siłę F.
Opisz ruch kołowrotu w zależności od kąta α jaki tworzy nić z kierunkiem
poziomym.
Wskazówki: Wygodnie jest traktować ruch kołowrotu jako obrót wokół
chwilowej osi A, przechodzącej przez punkty, w których kołowrót styka się z podłożem. Taki obrót uwarunkowany jest tylko momentem siły F względem osi A. Momenty pozostałych sił: tarcia T oraz ciężkości i reakcji podłoża (niezaznaczonych na rysunku) wynoszą 0. Zatem: M = F x = IA ε, Oblicz x korzystając z zależności trygonometrycznych.
Wyznacz moment bezwładności względem osi A korzystając z twierdzenia Steinera. Oblicz z wzoru na
moment siły przyspieszenie liniowe a (jaka jest zależność między przyspieszeniem liniowym a kątowym?).
Przeanalizuj, przy jakich kątach a > 0, < 0, = 0. Kiedy przyspieszenie kątowe = 0? Rozważ ruch postępowy szpuli w takich warunkach.
14. Na szczycie gładkiej kuli o promieniu R położono monetę, która będąc w położeniu równowagi chwiejnej zaczęła się zsuwać. W którym miejscu, licząc od wierzchołka luki, moneta oderwie się
od niej (moneta zsuwa się bez tarcia)?
Wyszukiwarka
Podobne podstrony:
Projekt grupa 3 2
ZARZĄDZANIE PROJEKTAMI grupa TVN
szablon opisu projektu 27-02-2012, 6 new BDiA
PROJEKT grupa 04
Logika projekt informacje, Uczelnia, II semestr, Logika Przywara Projekt grupa GPLog01, SPLog01, SPL
projekt 188 02 01 DMR 2011
grupa 02 zajecia nr 33
PROJEKT grupa 05
zarządzanie projektem pkt 02
Budownictwo ogólne projekt Model (02)
PMG PROJEKT 1 grupa
mechanika budowli projekt (28 02 2010 r )
grupa 02 zajecia nr 1
projekt 12 02
grupa 02 zajecia nr 44
więcej podobnych podstron