1

1.1 Opis układów dynamicznych liniowych stacjonarnych w przestrzeni stanów postać równań stanu

•

=

+

x( t)

Ax( t)

Bu( t)

y( t) = Cx( t) + Du( t)

A-macierz stanu n/n

m- liczba wejść

B- macierz wejść n/m

p- liczba wyjść

C- macierz wyjść p/n

n- rząd zmiennych stanu, równy rzęd.

D- macierz transmisyjna p/m

1.2 postać rozwiązania

A t − t

A t

0

τ

x( t)

(

)

( )

= e

x

0 +

e

Bu( t)

∫ −

τ

d

1.3 pojęcie biegunów

miejsca zerowe wielomianu charakterystycznego o postaci:

n

n 1

W ( s) = det( sI − )

A = s + a s −

−

+ ...+ a s + a

n 1

1

0

1.4 wartości własne i wektory własne macierzy stanu A

są to miejsca zerowe wielomianu charakterystycznego

n

n 1

W ( s) = det( sI − )

A = s + a s −

−

+ ...+ a s + a

n 1

1

0

wartości własne macierzy stanu A oznaczane są:

si (i=1,2,3…n)

1.5 Wektory własne macierzy stanu A (mody):

Jeżeli si jest wartością własną macierzy stanu A to odpowiadający jej wektor własny vi obliczamy ze wzoru: ( s I

A v

i

− ) i = 0

przy czym βi (i=1,2,3…n) są to współczynniki rzeczywiste, natomiast vi są to wektory własne macierzy A

2. Sterowalność i obserwowalność układów dynamicznych liniowych stacjonarnych 2.1 Pojęcie sterowalności

UKŁAD 1 NAZYWAMY CAŁKOWICIE STEROWALNYM (KRÓTKO STEROWALNYM), JEŻELI STOSUJĄC

OGRANICZONE

PRZEDZIAŁAMI

CIĄGŁE

STEROWANIE

U(T)

MOŻNA

GO

PRZEPROWADZIĆ Z DOWOLNEGO ZADANEGO STANU POCZĄTKOWEGO X0 DO ZADANEGO

STANU KOŃCOWEGO XK = X(TK) W SKOŃCZONYM CZASIE ZWYKLE PRZYJMUJE SIĘ XK=0.

Układ jest sterowalny ó rząd macierzy S jest równy „n”, gdzie macierz S liczy się ze wzoru:

S

[

2

n 1

B

AB

A B

A −

=

K

B]

dla układów jednowymiarowych warunek sterowalości: det(S)≠0

Para macierzy AB jest nazywana parą sterowalną.

2.2 Pojęcie sterowalności:

UKŁAD NAZYWAMY OBSERWOWALNYM, JEŻELI ISTNIEJE TAKA SKOŃCZONA CHWILA TK, ŻE

NA PODSTAWIE ZNAJOMOŚCI STEROWANIA U(T); TЄ[T0;TK] I ODPOWIEDZI Y(T); TЄ[T0;TK], MOŻNA WYZNACZYĆ STAN POCZĄTKOWY X0 W CHWILI T0.

Układ liniowy 1 jest obserwowalny ó rząd macierzy O jest równy n gdzie: PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

2

 C 





 CA 

O = 

2

CA 





 M 

 n−1

CA







Warunek podany w powyższym twierdzeniu można zapisać w postaci: rząd O = n.

Parę macierzy (C;A) dla których spełniony jest powyższy warunek nazywamy parą obserwowalną.

Warunek O=n jest spełniony ó w macierzy O istnieje n dowolnie wybranych wierszy, z których można utworzyć macierz nieosobliwą o wymiarach n na n.

Dla układów jednowymiarowych warunek obserwowalności: det O≠0

2.3 DEKOMPOZYCJA KALMANA

- Postać kanoniczna Kalmana równań stanu. Dzieli układ na częśći

 A

A

A

A 

 B 

33

34

31

32

3





 

0

A

0

A

B

44

42

4

A = 

 B =  

C = [0 C

0

C

4

2 ]

 0

0

A

A 

 0 

11

12





 

0

0

0

A

0



22 

 

Z punktu widzenia sterowalności i obserwowalności dowolny układ dynamiczny można podzielić na cztery rozłączne części:

1. część niesterowalna i nieobserwowalna

2. część niesterowalna i obserwowalna

3. część sterowalna i nieobserwowalna

4. część sterowalna i obserwowalna

Macierz transmitancji operatorowej G(s) układu 1 zależy tylko od macierzy A44 B4

−1

−

C

=

−

+ =

4

−

1

44

4 +

4 i D to znaczy: G( s)

C( sI

A) B D C ( sI

A ) B

D

Macierz transmitancji operatorowej G(s) daje informacje tylko o właściwościach dynamicznych części sterowanych i obserwowanych. Nie daje żadnych informacji o właściwościach pozostały5ch trzech części.

3. Przesuwanie biegunów za pomocą sprzężeń zwrotnych od wektora stanu

Warunkiem przesuwania biegunów jest sterowalność obiektem:

S

[

2

n 1

B

AB

A B

A −

=

K

B]

rząd S=n, lub dla układów jednowymiarowych: det(sI – A)!=0

Istnieją 2 metody przesuwania biegunów:

1. Analityczna:

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

3

Liczymy

WC ( s)

n

n 1

= s +

−

a

s

.....

n 1

−

liczymy A

- Bk = uzyskująz

X

macierz

liczym det

y

(sI-(A-Bk) uz

i

ykujemy

z

równanie

porównujemy „z” współczynniki ze współczynnikami Wc(s) i mamy k1

k2 itd

2. Metoda Ackerman’a

Liczymy:

−

W

=

+

1

−

...

1

+

1

+

C ( s )

s n

a

s n

a s

a

n

0

Podstawiając za

"

uz

A

macirz

s"

yskuj

W

emy

C ( A)

−

Stosująt

K

wzór

= [0 0 ... ]

1 ⋅ S 1 ⋅ WC ( A)

Wyliczamy wektor sprzężeń K

4. Obserwator układów liniowych stacjonarnych.

4.1 podstawowe założenia, postać obserwatora pełnego rzędu

Warunki:

a) rank(S) = n gdzie S jest macierzą sterowalności i ma postać:

S

[ A AB A 2

=

B]

b) rank( O) = n jest równy n gdzie O ma postać:

 C 





O =  CA 



M





n−1 

 CA 

Równanie obserwatora (ogólne)

x

~&( t) = x

F~( t) + Gu( t) + Hy( t)

x

~

0 = x

~( t 0 )

~

n

x ∈ R

ε( t) = x( t) ~

− x( t) - błąd estymacji

Równanie stanu obserwatora:

x& = ( A − HC)~ x + ( H + Bu( t) + Hy (8)

Aby układ obserwatora odtwarzał wektor stanu x(t) należy tak dobrać macierze F, G, warunek aby spełniały warunek: lim ε ( t) =

( x( t) ~

lim

− x( t) = 0

t→∞

t→∞

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

4

Warunek ten jest spełniony ⇔ wartości własne macierzy F mają ujemne części rzeczywiste (leżą w OLP). Wartości własne macierzy F są miejscami zerowymi jej wielomianu charakterystycznego WF(S)=det(sI-F)

ε&( t) = Fε( t)

Oznaczmy przez:

F

F

F

S , S , S

wartości własne macierzy F

1

2

n −

Podstawiając wzory (9) do równania obserwatora (5) otrzymamy:

~

x& ( t) = ( A − HC)~ x + Bu( t)+ Fy

~

x& ( t)

~

= x

A ( t)+ Bu( t)+ H ( y( t)

~

− Cx( t)

( )

13

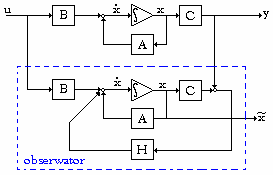
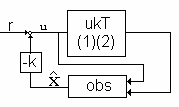
Równanie (13) jest równaniem obserwatora pełnego rzędu dla układu opisanego równaniami (1) (2). Schemat blokowy układu (1) (2) z obserwatorem (13) przedstawia poniższy rysunek.

Przy projektowaniu obserwatora (13)

należy tak dobrać macierz H, aby

wartości własne macierzy F=A-HC

leżały w OLP na lewo od biegunów

układu (1) (2) (wartości własnych

macierzy A). Jest to związane z

szybkością zanikania przebiegu ε(t) czyli

szybkością z jaką x

~( t)→ x( t)

0

 

− 0

w celu wyznaczenia obserwatora stosujemy wzór Ackerman’a: H = W

F ( A) ⋅

1

O  

M

 

1

4.2 Obserwator zredukowany

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

5

xa ( t) = x t = y t

1 ( )

( )

 x t 

2 ( )

x

M

b ( t )





= 



 xn( t)

Równania

napiszem

(2)

(1)

stanu

w

y

postaci

:

x& t   A

A

aa

ab 

 x t

a

  Ba 

a ( )

( )



u t

 x& b( t) =

⋅

 

 

  A

A

ba

bb   xb ( t ) +

⋅

   ( )

(22)



B

4

1

4

2 3

{

 b 

A

b

y( t) = [

 x t

a



1 0 ... 0 ]

( )

⋅ ⋅  xb( t)

(23)



Powyższe równanie (22) można napisać w postaci dwóch równań:

x& = A x + A x + B u

22

b

ba a

bb b

b

( a)

x& = A x + A x + B u

22

a

aa a

ab b

a

( b)

Równanie (22a) przekształcamy do postaci:

& x = A x +

A x + B u

b

bb b

ba

a

b

(24)

4

43

42

1

wielkośi

mo

znana,

żoż

ją traktowa

ć

wej

jako

śwej

Przekształcając (22b) otrzymamy:

y& − A x

B u

A x

aa

a −

a

= ab b − możoż traktowa ćj

w

ako

yjśwyj

(25)

Równania (24) i (25) można traktować jako równania stanu dla którego obserwator pełnego rzędu będzie obserwatorem zredukowanym.

~

~

X = A ⋅ x + A y + B u + H y& − A y − B u − A x B

BB

b

ba

b

(

aa

a

)

~

ab

b

(26)

oznaczmy przez ε = x

x

~

− błąd obserwacji

b

b

b

0

 

−

0

Stosując metodę Ackerman’a obliczamy: H = Wε ( A

W

bb ) ⋅

1

O

⋅  



ε(s) - zadany wielomian

M 

 

1

charakterystyczny obserwatora

Przekształcając równanie (26) otrzymamy:

~

x& =

−

+

−

+

−

+ &

b

( A H

ab

ab )~

xb ( A

HA

ba

aa ) y

( B HB

b

a ) u

Hy

(32)

Ab unikn

y

ąn ró

żóżniczk ania

odpowiedzi

y(t)stosu

je si

ę now

y

r

wekto

~

x = x − Hy

c

b

(33)

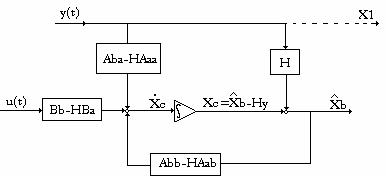
Przy oznaczeniu (33) równanie obserwatora (32) napiszemy w postaci:

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

6

x =

−

~

&

+

−

+

−

- równaniem różniczkowe

c

( A

H

ab

ab ) xb

( A

HA

ba

aa ) y

( B HB

b

a ) u

obserwatora zredukowanego dla układu (1) (2) przy p = m = 1.

5. Przesuwanie biegunów z zastosowaniem obserwatora

Założenie: Układ jest sterowalny i obserwowalny.

Jeżeli są dostępne zmienne stanu to do przesuwania biegunów stosuje się sprzężenie zwrotne u = - kx. Jeżeli nie wszystkie zmienne stanu są niebezpośrednio dostępne i układ jest obserwowalny to możemy zastosować obserwator (lub obserwator zredukowany) do odtworzenia niedostępnych zmiennych stanu.

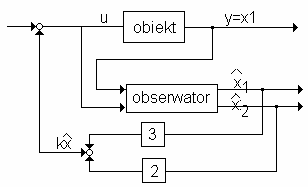
Przy zastosowaniu obserwatora pełnego rzędu do przesuwania biegunów w układzie (2) stosujemy sprzężenie zwrotne:

~

u = − x

k + r( t)

( )3

gdzie x

~ jest to estymata wektora x.

Równanie stanu ze sprzężeniem zwrotnym ma postać:

~

x& = Ax −

x

Bk + r

(4)

Przyjmujemy: ε = x − x~ → x~ = x − ε

Równanie (4) możemy zapisać w postacie:

x& = Ax − Bk( x − ε ) = ( A − Bk) x +

ε

Bk

(5)

Jest to równanie układu zamkniętego.

Dla obserwatora spełnione jest następujące równanie:

ε& = ( A − HC) ε

(6)

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

7

Za zmienne stanu układu z obserwatorem przyjmujemy zmienne stanu układu (1) (2) oraz elementy wektora ε.

Nowy wektor stanu układu zamkniętego ma postać:

 x

 

 ε 

Równanie (5) i (6) można napisać w postaci:

 x&  A − Bk

Bk

  x

=

⋅

  

  

 ε&  0

A − HC  ε 

1

4

4

4

2

4

4

4

3

macierze

ukadu

stanu

zamkni

ę

o

amk

em

obserwator

z

Wielomian układu zamkniętego z obserwatorem:



 A − Bk

Bk



det⋅ sI

 − 



0

A − HC 







 sI − ( A − Bk)

− Bk



det =

=

sI − A − Bk ⋅

sI − A − HC





0

sI



− ( A − HC) det(

(

) det(

(

)

(7)

1

4

4

4 2

4

4

4 3 1

4

4

4

2

4

4

4

3



WC ( s)

WF ( s)

Wielomian charakterystyczny układu zamkniętego można przedstawić w postaci (7) Równanie stanu obserwatora:

x& = ( A − HC)~ x + ( H + Bu( t) + Hy (8)

Ze wzoru (7) wynika, że synteza sterowania modalnego przesuwającego bieguny układu (1) (2) do zadanych położeń oraz synteza obserwatora (8) można przeprowadzić niezależnie.

Macierz H sterowania modalnego wybieramy tak, aby wielomian charakterystyczny Wc(s)=det⋅(sI-(A-Bk)) układu zamkniętego bez obserwatora miał zadane miejsca zerowe, będące biegunami układu (1) (2) bez obserwatora.

Macierz H dobieramy tak aby wielomian charakterystyczny WF(s)=det⋅(sI-(A-HC)) obserwatora miał zadane miejsca zerowe będące zadanymi biegunami obserwatora. Należy pamiętać aby bieguny obserwatora leżały w otwartej lewej półpłaszczyźnie, na lewo od biegunów układu zamkniętego (miejsc zerowych wielomianu WC(s).

Przesuwanie:

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

8

•

x( t) = Ax( t) + Bu( t)

y( t) = Cx( t)

0



1

0

A =

B =

C =





 

[1 0]

0

0

1





 

y( t) = x t

1 ( )

−

W ( s)

s

= det( sI − A)

1

2

=

= s

0

s

przyjmujemy, że chcemy przesunąć bieguny układu do położeń:

2

s

= 1

− ± 2

,

1 2

Sprawdzamy Sterowalność: rank(O) i (S) = n

Aby wielomian charakterystyczny A-Bk miał zadane miejsca zerowe s c

11

det⋅(sI-(A-Bk)) = (s-s 2

2

1 )⋅(s-s2 ) = s2+2s3 i jest to Wc(s)

stosując wzór Ackerman’a;k=[0 1]⋅s-1⋅Wc(A)

Przeprowadźmy syntezę obserwatora pełnego rzędu:

Należy tak dobrać macierz H:

 h 1 

H =  

 h 2 

Przyjmujemy bieguny obserwatora:

sF = − 5

,

2 ± j 3

,

4

,

1 2

W ( s) = det( sI − ( A − HC) = ( s − sF

F

⋅ s − sF = s + s +

1 ) (

2 )

2

5

74

,

24

Stosując wzór Ackerman’a otrzymamy:

0

5

}

1

  



H =

−

W

⋅

⋅

=

1

F ( A)

h

O

  



1

,

24 74

h

  

} 2

 −

5

1  x~

8

1 ( t )





A − HC =

⋅

⋅

+

⋅



  ~ 





− ,

24 74

0

x



  ( t) u( t)

y( t)



 ,

24 74

1

G( s) =

− obiekt

s 2

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

9

6. Sterowanie optymalne przy kwadratowych wskaźnikach jakości (sterowanie optymalne)

Weźmy pod uwagę wskaźnik jakości sterowania o postaci:

∞

I = ∫ ( xT ( t) Qx( t)+ uT ( t) Ru( t)) dt (2)

0

Gdzie macierz Q i R są to rzeczywiste symetryczne dodatnio określone macierze, przy czym Q∈Rnxn

R∈Rmxn

Często przyjmuje się, że są to macierze diagonalne (zerowe elementy poza głównej przekątną):

 a 0 0





0 a 0

0 0 c





Macierz x jest dodatnio określona ⇔ są dodatnie wszystkie jej główne podwyznaczniki, tzn.: D = x > 0

1

11

 x

x 

11

12

D =

> 0





2

 x

x

21

22 

.............................

D = det x > 0

4

Zadanie:

Należy wyznaczyć macierz K sprzężenia zwrotnego

U(t) = - kx(t)

(3)

Tak, aby sterowanie (3) minimalizowało wskaźnik jakości (2). Będziemy przyjmować, że na sterowanie u(t) nie nakłada się żadnych ograniczeń.

Problem wyznaczenia (3), które minimalizuje wskaźnik (2) nazywa się syntezą regulatora LQR (Linear Quadratic Regulator)

Przeanalizujemy bliżej wskaźnik jakości (2).

∞

xT ( t) Qx( t)

∫

dt Przedstawia ważoną sumę kwadratów odchyleń zmiennych stanu od początku układu 0

współrzędnych współrzędnych. W przestrzeni stanu wagami są elementy macierzy Q. Fizycznie przedstawia straty sterowania.

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

10

∞

Wyrażenie uT ( t) Ru( t) dt

(5)

∫

0

Przedstawia ważoną sumę kwadratów wielkości sterującej. przedstawia wydatek energii sterowania (koszt sterowania). Stosuje się je we wskaźniku w celu zapobieżenia zbyt dużym wartościom amplitud optymalnych sygnałów sterujących.

Rozwiązanie postawionego problemu jest zawarte w poniższym twierdzeniu:

Macierz K sprzężenia zwrotnego (3), które minimalizuje wskaźnik jakości (2) przy zadanych macierzach Q i R oblicza się ze wzoru:

1

−

K = R

B T P

(6)

gdzie macierz P jest macierzą symetryczną dodatnio określoną będącą rozwiązaniem macierzowego równania Riccatie’go o postaci:

T

1

A P + PA −

−

PBR BT P + Q = 0

(7)

Równanie (7) nazywane jest ZREDUKOWANYM RÓWNANIEM RICCATIEG’O.

W pewnych przypadkach macierz P będącą rozwiązaniem równania (7) może nie być dodatnio określona. Postawione zadanie ma rozwiązanie gdy macierz P jest dodatnio określona.

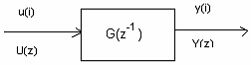
7. Model transmitancyjny dyskretnego obiektu liniowego stacjonarnego

U(i)=u(iTp) Tp- okres próbkowania

Ogólna postać transmitancji G(

1

−

z ) ma postać

Y ( z)

−

− d B(

1

−

z

1

)

= G( z ) = z

(1)

U ( z)

( 1

−

A z )

−1

−1

− n

B( z ) = b 0 + b z

1

+ .... + b z

n

(2)

−1

−1

− n

A( z ) = 1 + a z

1

+ .... + a z

n

d- dyskretny czas opóźnienia

Relacja pomiędzy wejściem i wyjściem w dyskretnych chwilach czasu może być zapisana w postaci :

y( i)

d B(

1

−

−

z )

= z

gdzie

1

−

z to operator opóźnienia o Tp

u( i)

( 1

−

A z )

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

11

Z powyższej zależności wynika równanie różnicowe,które odpowiada transmitancji dyskretnej (1)

y( i) + a y( i − )

1 + ... + a y( i − n) = b u( i − d ) + b n( i − d − ) 1 + ... + b n( i − d − n)

(3)

1

n

0

1

n

Charakterystyka impulsowa g(i) jest to odpowiedź obiektu dyskretnego na impuls Kroneckera δ(i) przy zerowych warunkach początkowych

1

dla

i = m

δ(i-m)= 

0

dla

i ≠ m

Zachodzi zależność

g(i)=

1

−

z { G( 1

−

z ) }

(4)

Odpowiedź układu dyskretnego na dowolne wymuszenie u(i) można wyrazić wzorem (splot dyskretny )

g(i)= ∑

∞

g( m) u( i − m)

(5)

m=0

Transmitancja (1)można napisać w postaci

n

−

b

( z

z )

1

n

−1

0 ∏

− k

−1

(

)

(

)

G( z ) = − B z

z B z

d

z

= − d

z

=

k =0

−

(6)

1

n

−

A( z )

z A( z 1 )

d

z ∏

n

( z − p )

k

z - zera transmitancji dyskretnej G(z 1

− )

k

p

bieguny transmitancji dyskretnej G(

1

−

z )

k −

Układ dyskretny jest :

=

a) asymptotycznie stabilny ó gdy p

,

1 k

,

1 2 ... n

k

b) stabilny ó gdy p ≤ ,

1 k = ,

1

n

...

2

k

c) niestabilny ógdy istnieje przynajmniej jeden biegun p

k

> 1

W zależności od zer rozróżnia się obiekty

a) minimalnofazowe dla których z ≤ ,

1 k = ,

1

n

..

2

k

b) nieminimalnofazowe jeżeli przynajmniej jedno zero spełnia warunek z k

> 1

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

12

7. Modele dynamiczne ciągów czasowych

7.1 Model AR

1

V ( i) =

−

D( z 1) e( i)

V

(i) = − d V

1

( i − )1−...− d V − +

p

( i p) e( i)

7.2 Model MA

V ( i) =

−

C( z 1 )⋅ e( i)

V ( i) = e( i) + C e( i − )

1

1

+ ... + C

−

q ( i

q)

Aby filtr F(z-1) był stabilny asymptotycznie jego wielomian charakterystyczny: musi mieć wszystkie zera zi położone wewnątrz okręgu jednostkowego.

Warunek minimalnofazowości jest tożsamy z warunkiem odwracalności. Spełnienie warunku odwracalności pozwala na wyznaczenie ciągu e(i) na podstawie znajomości V(i).

7.3 Model ARMA

−1

−

F ( z 1) C( z )

=

−

D( z 1) e( i)

V ( i) = − d

1 ( V −1 − ... −

− +

+ 1 −1 +...+

−

i

)

d V

p

( i p) e( i) C e( i )

C e

q ( i

q)

Jest to dynamiczny model różnicowy pobudzany szumem białym.

D – operator autoregresyjny

9. Modele dynamiczne obiektów dyskretnych

9.1 MODEL ARARX (ang. AutoRegressive, AutoRegressive with eXogenous variable):

−

− d B(

1

z

)

1

y( k) = z

u( i)+

ε( i)

−

−

−

;

(

1

A z )

D(

1

z ) (

1

A z )

9.2 MODEL ARX (ang . AutoRegressive with eXogenous variable):

−

− d B(

1

z

)

1

y( k) = z

u( i)+

ε( i)

−

−

;

(

1

A z )

(

1

A z )

9.3 MODEL ARMAX (ang. AutoRegressive Moving Average with eXogenous variable):

A(z-1) y(i) = B(z-1) u(i-d) + C (z-1) ε (i) ;

9.4 MODEL BJ (model Boxa-Jenkinsa):

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

13

−

−

− d B(

1

z )

C(

1

z )

y( k) = z

u( i)+

ε( i)

−

−

;

(

1

A z )

D(

1

z )

10. Identyfikacja charakterystyk statycznych metodą najmniejszych kwadratów.

Identyfikacja ma charakter iteracyjny i obejmuje:

1) Wybór struktury modelu z określonej klasy modeli na podstawie aktualnej znajomości obiektu

2) Estymacje wartości liczbowych parametrów modelu na podstawie pomiarów wielkości wejściowych i wyjściowych podczas doświadczeń identyfikacyjnych

3) Sprawdzenie dokładności przewidywań za pomocą wyznaczonego modelu.

Wykorzystujemy przy tym zbiór wielkości wejściowych i wyjściowych najczęściej różne od zbiorów użytych przy doświadczeniach identyfikacji

4) Przeprowadzenie estymacji parametrów dla modelu algorytmów odmiennej strukturze, jeżeli dokładność przewidywań za pomocą wyznaczonego modelu okaże się nie

wystarczająca.

Metoda najmniejszych kwadratów: (Least Swuare)

MNK najczęściej stosuje się do estymacji modelów parametrycznych. Metoda ta umożliwia estymację parametrów takich modeli statycznych, w których wielkość wyjściowa jest liniową funkcją estymowanych parametrów. Nie musi być ona liniowa ze względu na wielkości wyjściowe.

Model statyczny algorytmów wymienionej powyżej własności można napisać w postaci: y = b + b

+

+ ... +

1

0

ϕ

1 1 ( u )

b ϕ

2

2 ( u )

b ϕ

m

m ( u )

( )

 u 

1

 

u

gdzie u

2

=  

j

wektor we

-

śść

ϕ

− funkcje

bo

liniowe

ąoą

wej

nieliiowe

ś u

w

i ( u )

 M 

 

u

 r 

b 

0

 

b =

M

ϕ( u) = [1 ϕ 1( u) L ϕm ( u)]

 

b 

 m 

Uwzględniając powyższe oznaczenia wzór (1) napiszemy w postaci y = ϕ(u)⋅b

(2)

b – wektor estymowanych parametrów modelu

przykład:

jeżeli np. model jest liniowy względem wejść to wzór (4) przyjmie postać:

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

14

 a 

ϕ

=

0

1 ( u )

u 1

 

a

ϕ

=

1

2 ( u )

u

b

2

=  

ϕ

= 1



M 

ϕ

=

3 ( u )

( u) [ u u u

1

2

r ]

u 3

 

a

ϕ u

 

= u

r

r ( )

r

Najczęściej dysponujemy pomiarami zakłóconymi. Wobec tego zamiast (2) należy zastosować: y = ϕ(u)⋅b + z

(3)

Gdzie z jest zakłóceniem sprowadzonym na wyjście obiektu.

Celem identyfikacji jest określenie parametrów modelu (2) (tj. określenie elementów wektora b na podstawie wyników N – doświadczeń identyfikacyjnych, N>>(m + 1).

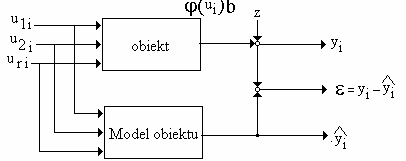
Doświadczeniem identyfikacyjnym i-tym nazywa się ustalenie wielkości wejściowych obiektu na wartościach u1i, u2i, uri oraz pomiar odpowiadającej im w stanie ustalonym wartości wyjściowej yi.

Dla każdego doświadczenia identyfikacyjnego definiuje się błąd identyfikacji εi jako różnicę wartości wielkości wejściowej obiektu y

~

i oraz wartości wielkości wyjściowej modelu yi .

Parametry modelu należy tak określić aby suma kwadratów błędów identyfikacji dla wszystkich doświadczeń identyfikacyjnych była minimalna:

N

N

N

2

min

2

∑ ε

y

ϕ u b

y

ϕ u b

i

=

∑( i − ( i)⋅ )2 =∑( i − ( i ) ˆ

min

⋅ )

(5)

b

b

i 1

=

i 1

=

i 1

=

 ˆ b 

0

 ˆ 

ˆ  b 1 

b =

j

tzw

est to

na

wedlug

ocena

jmniej y

sz ch

modelu

b

parametrów

kwadratów

 M 

 ˆ 

 bm 

Wyznaczenie wektora b z daszkiem zgodnie ze wzorem (5) nazywa się estymacją według najmniejszych kwadratów.

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

15

Idea algorytmów rekurencyjnych identyfikacji.

Rekurencyjny algorytm najmniejszych kwadratów przy identyfikacji

charakterystyk statycznych

Załóżmy, że mamy k- doswiadczen ident.

bˆ k – wektor ocen parametrów otrzymany w wyniku przeprowadzenia k-doświadczeń ident.

Zgodnie ze wzorem:

ˆ

T

1

−

b = ( U U )

T

U y

mamy

ˆ b

P U y

k =

T

k

k

k

T

1

−

P

U U

k = (

)

k

k

Wykonanie doświadczenia identyfikacyjnego k+1 daje nowy element yk+1 oraz nowy wiersz macierzy U o postaci:

ϕ( u )

ϕ u

ϕ u

k

= 1

[

(

)...

(

)

1

+

1

k 1

+

m

k 1

+

Uwzględnienie doświadczenia k+1 pozwala na uaktualnienie oceny parametrów.

b ^

= b^ + k ( y

− ϕ b^ )

k 1

+

k

k 1

+

k 1

+

k

k 1

+

T

k

= P ϕ

gdzie

k 1

+

k 1

+

k 1

+

T

P ϕ

ϕ P

k

k

k 1

+

k

P

= P

1

+

−

k 1

+

k

T

1 + ϕ

P ϕ

k

k 1

+

k 1

+

Po

eniach

przeksztac

y

otrzymujem

T

P ϕ

k

k

k

1

+

=

k 1

+

T

1 + ϕ

P ϕ

k

k 1

+

k 1

+

W kolejnym doświadczeniu ident na bazie pomierzonych wartości we i wy tworzymy wektor ϕk+1 oraz obliczamy macierz Pk i następnie obliczamy wektor bˆ k+1.

Wraz ze wzrostem indeksu k elementy macierzy Pk maleją monotonicznie (znikają).

• Podany przy identyfikacji charakterystyk statycznych rekurencyjny algorytm najmniejszych kwadratów można bezpośrednio stosować do rekurencyjnych identyfikacji modeli dynamicznych.

Ma on postać:

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

16

^

^

^

b ( i + )

1 = b ( i) + k( i + )[

1 y( i + )

1 − ϕ ( i + )

1 b ( i)]

P( i) T

ϕ ( i + )

1

k( i + )

1 = α + ϕ( i + )1 P( i) T

ϕ ( i + )

1

1

P( i) T

ϕ ( i + )

1 ϕ ( i + )

1 P( i)

P( i + )

1 =

[ P( i) −

α

α + ϕ( i + )

1 P( i) T

ϕ ( i + )

1

α −

k

wspóczynni zapo min ania

T

1

P( i)

( φ φ )−

= i i

W przypadku układów stacjonarnych (parametry stałe w funkcji czasu) α=1. Dla obiektów o powoli zmniejszających się parametrach przyjmuje się najczęściej, że 0,95≤α≤0,995.

Wykład 13

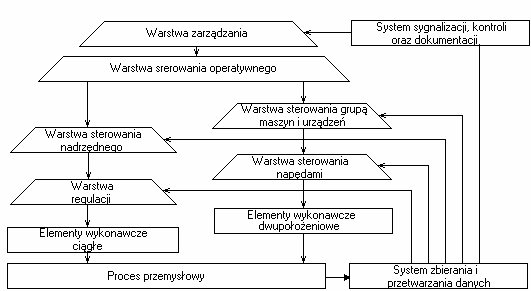
Struktura funkcjonalna systemów automatyki przemysłowej.

-określa zestaw zadań realizowanych przez system oraz powiązania między nimi.

-charakteryzuje się hierarchicznością powiązań miedzy etapami procesu.

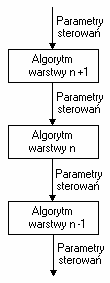
Struktury hierarchiczne:

- w wyniku realizacji algorytmu warstwy wyższej otrzymuje się parametry

niezbędne do realizacji algorytmu warstwy niższej.

a) prosta:

b) piramidalna:

Systemy sterowania

Systemy sterowania

zmiennymi procesowymi

zmiennymi procesowymi

binarnymi

ciągłymi

ad.a) -algorytm wyższej warstwy wypracowuje parametry tylko dla jednej warstwy niższej.

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com

17

ad.b) -algorytm wyższej warstwy wypracowuje parametry dla wielu algorytmów warstw niższych.

W szczególnym przypadku algorytm warstwy wyższej może decydować który z algorytmów warstw niższych ma być aktualnie realizowany. Jest to „Struktura hierarchiczna z priorytetem warstw wyższych”.

W układach automatyki przemysłowej mamy do czynienia ze strukturami piramidalnymi.

PDF created with FinePrint pdfFactory Pro trial version http://www.pdffactory.com