Ćwiczenie projektowe z fundamentowania nr2
- 1 -
_
Politechnika Poznańska
Instytut Inżynierii Lądowej
Zakład Geotechniki i
Geologii Inżynierskiej
Prowadzący: dr inż. J.Rzeźniczak
ĆWICZENIE PROJEKTOWE Z
FUNDAMENTOWANIA
NR 2
Daniel Sworek gr. B8
Rok akademicki 07/08
Semestr 4
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 2 -
_
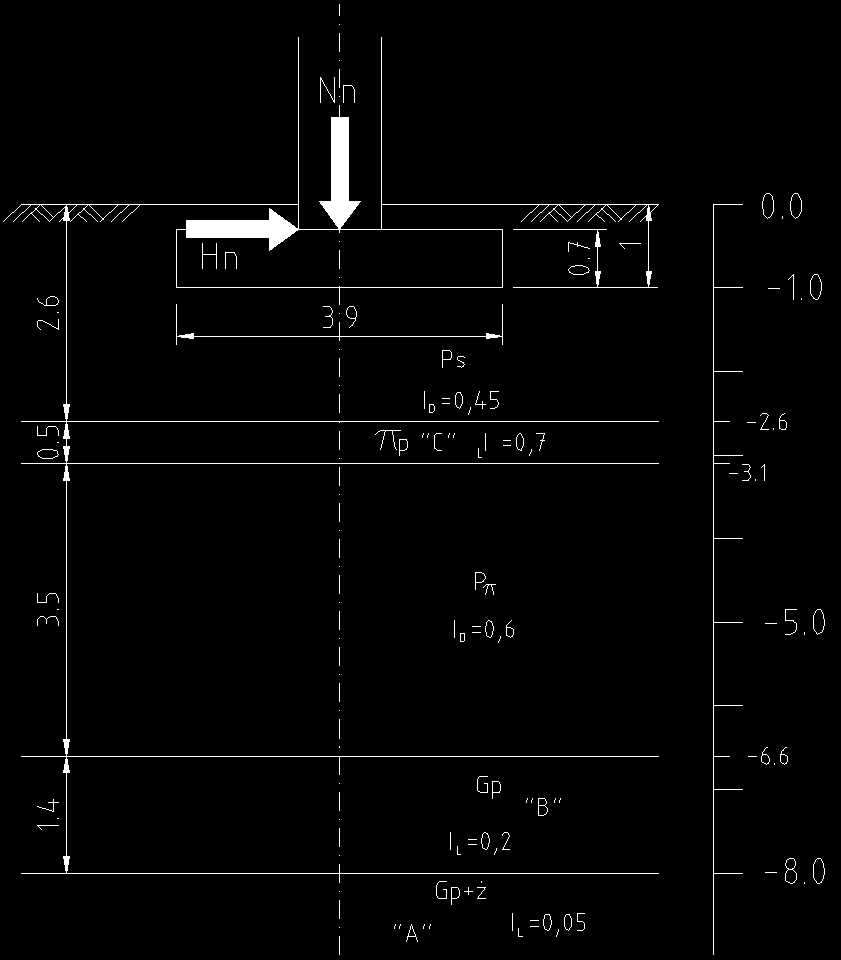
ZADANIE: Zaprojektować posadowienie bezpośrednie (stopy fundamentowe) dla stalowej hali dla podanych obciążeń charakterystycznych (stałych i zmiennych długotrwałych) oraz warunków gruntowo-wodnych.
Charakterystyka gruntów występujących w podłożu:
y
j
er
a
γ
za
tu
p
w
s
n
tu
kN
Φ
m
et.
d
n
n
u
kN
n
γ
u
rstw
I
c
o
ta
3
ru
ru
en
L
ID
Sr
[%]
u
m
[˚]
3
S
ru
N
a
g
w
R
g
G
m
g
w
I
Ps
-
-
0,45
0,5
14,0
26,5
18,5
-
32,6
szg
II
πp
C
0,7
-
-
22,0
26,6
mpl
20,0
6,0
6,8
nw
1 ,
9 0
III
P
π
-
-
0,6
1,0
24,0
26,5
szg
5
,
9 7
-
31,0
IV
Gp
B
0,2
-
-
12,0
26,7
tpl
22,0
31,5
18,3
G
V
p
A
0,05
-
-
12,0
26,7
tpl
22,0
47,0
24,2
+ż
Warstwa 1:
3
γ = 8
,
1 5 ⋅1 ,
0 0 = 18 5
, kN m
Warstwa 2:
3
γ = ,
2 0 ⋅1 ,
0 0 = 2 ,
0 0 kN m
Warstwa 3:
γ
γ − γ
100 ⋅
10 ,
0 0 ⋅ 9
,
1 ⋅1 ,
0 0
' = (γ − γ
⋅ 1− ;
s
d
n =
;
3
=
γ
γ
=
= 15 3
, 2 kN m ;
s
) ( n
w
)
γ
d
100 + w
10 ,
0 0 + 2 ,
4 0
s
γ
γ
s −
26 5
,
d
−15 3
, 2
n =
=
= ,
0 4 [
2 −] γ =
−
⋅ −
=
γ
; ' (26 5
,
1 ,
0 0) (1
,
0 42))
3
5
,
9 7 kN m
26 5
,
s
Warstwa 4:
3
γ = ,
2 2 ⋅1 ,
0 0 = 2 ,
2 0 kN m
Warstwa 5:
3
γ = ,
2 2 ⋅1 ,
0 0 = 2 ,
2 0 kN m
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 3 -
_
Przed przystąpieniem do projektowania fundamentów zlecam wykonanie nasypu w miejscu, gdzie zostanie posadowiona stopa fundamentowa nr 1, do poziomu terenu, gdzie zostanie posadowiona stopa fundamentowa nr 2. W tym celu zostaje przywieziony piasek średni, który po rozplantowaniu zostaje zagęszczony do stopnia zagęszczenia: ID=0,45, aby otrzymać równy poziom terenu oraz jednorodny grunt.
I STAN GRANICZNY:
Stopa nr 1:
Fundament rzeczywisty:
B = 3,9 m (szerokość stopy)
L = 3,9 m (długość stopy)
D = 1,0 m (zagłębienie)
H = 0,7 m (wysokość stopy)
3
γ =
ś
2 ,
2 0 kN m
r
Warunek I:
q
≤ m ⋅ q
rs
f
m = 9
,
0 ⋅ 9
,
0
= 8
,
0 1
N + B ⋅ L ⋅ D
⋅γ
155 ,
0 0 + 9
,
3 ⋅ 9
,
3 ⋅ ,
1 0 ⋅ 2 ,
2 0
kN
n
min
q
śr
=
=
= 123 9
, 1
n
2
B ⋅ L
B ⋅ L
m
kN
q
= 123 9
, 1⋅ ,
1 2 = 14 ,
8 69
rs
2
m
B
B
B
( r )
( r )
( r )
q = 1 + 3
,
0 ⋅
⋅ N ⋅ c
+ 1+ 5
,
1 ⋅
⋅ N ⋅ D
⋅γ + 1− ,
0 25 ⋅
⋅ N ⋅ B ⋅γ
f
C
u
D
min
D
B
B
L
L
L
( r )
φ
;
n
= 3 ,
2 6 ⋅ 9
,
0
= 29 3
, 4°
( r )
c
(grunt niespoisty);
n
= ,
0 0
N
;
N
;
N
;
B =
8
,
6
D = 17 1
, 1
C = 2 ,
8 64
( r )
3
γ
= 18 5
, ⋅ 9
,
0
= 1 ,
6 65 kN m ;
D
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 4 -
_
⋅
+
−
⋅
+
⋅
r
18 5
,
,
1 6
20 10
5
,
0
5
,
9 7
8
,
1
( )
(
)
3
γ
=
⋅ 9
,
0
= 1 ,
3 29 kN m ;
B
9
,
3
9
,
3
9
,
3
q = 1 + 3
,
0 ⋅
⋅ 2 ,
8 64 ⋅ ,
0 0 + 1 + 5
,
1 ⋅
⋅17 1
, 1⋅ ,
1 0 ⋅1 ,
6 65 +
f
9
,
3
9
,
3
9
,
3
kN
+ 1− ,
0 25 ⋅
⋅ 8
,
6 ⋅ 9
,
3 ⋅1 ,
3 29 = 976 5
, 4
3
9
,
3
m
2
2
14 ,
8 69 < 8
,
0 1⋅ 976 5
, 4 ⇒ 14 ,
8 69 kN m < 79 ,
1 0 kN m (warunek spełniony).
Warunek II:
N ≤ m ⋅ Q
;
r
fNB
m = 9
,
0 ⋅ 9
,
0
= 8
,
0 1 ;
G = N + B ⋅ L ⋅ γ
= 1550 + 9
,
3 ⋅ 9
,
3 ⋅ ,
1 0 ⋅ 2 ,
2 0 = 188 ,
4 62
;
ś
kN
n
n
r
N = ,
1 2 ⋅ G = ,
1 2 ⋅188 ,
4 62 = 2261 5
, 4 kN ;
r
n
Sprawdzenie, czy siła działa w rdzeniu przekroju: M = N ⋅ e ;
r
r
B
M = H ⋅ H , gdzie M = H ⋅ H ; r
r
r
r
H r ⋅ H
75 0
, ⋅ ,
1 2 ⋅ 7
,
0
e
;
B =
=
=
B
0
,
0 28 <
= 6
,
0 5
N
2261 5
, 4
6
r
B
( )
B
r
Q
L B 1
3
,
0
N
i
c
1
5
,
1
N
i
D min γ
fNB =
⋅ +
⋅
⋅ C ⋅ C ⋅ n + + ⋅
⋅ D ⋅ D ⋅
⋅ D +
L
L
B
+ 1− ,
0 25 ⋅
⋅ N i B γ
B ⋅ B ⋅
⋅
B
L
L = L = 9
,
3 m ;
B = B − 2 ⋅ e = 9
,
3 − 2 ⋅ ,
0 028 = 8
,
3 44 m ;
B
H
tan δ
tan ( r)
φ
;
tan δ =
r = 0
,
0 3979589 ;
= ,
0 071 ;
n
= 5
,
0 6209217
N
tan ( r)
φ
r
n
i
;
i
;
i
;
B =
9
,
0 3
D =
9
,
0 6
C =
9
,
0 6
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 5 -
_
8
,
3 44
8
,
3 44
Q
= 9
,
3 ⋅ 8
,
3 44 ⋅ 1 + 3
,
0 ⋅
⋅ 28 6
, 4 ⋅ 9
,
0 6 ⋅ 0
,
0
+ 1+ 5
,
1 ⋅
⋅17 1
, 1⋅ 9
,
0 6 ⋅ ,
1 0 ⋅1 ,
6 65 +
fNB
9
,
3
9
,
3
8
,
3 44
+ 1− ,
0 25 ⋅
⋅ 8
,
6 ⋅ 9
,
0 3 ⋅ 8
,
3 44 ⋅1 ,
3 29 = 1381 ,
1 6 k
1 N
9
,
3
2261 5
, 4 < 8
,
0 1⋅13811 6
, 1 ⇒ 2261 5
, 4 kN < 1118 ,
7 40 kN (warunek spełniony).
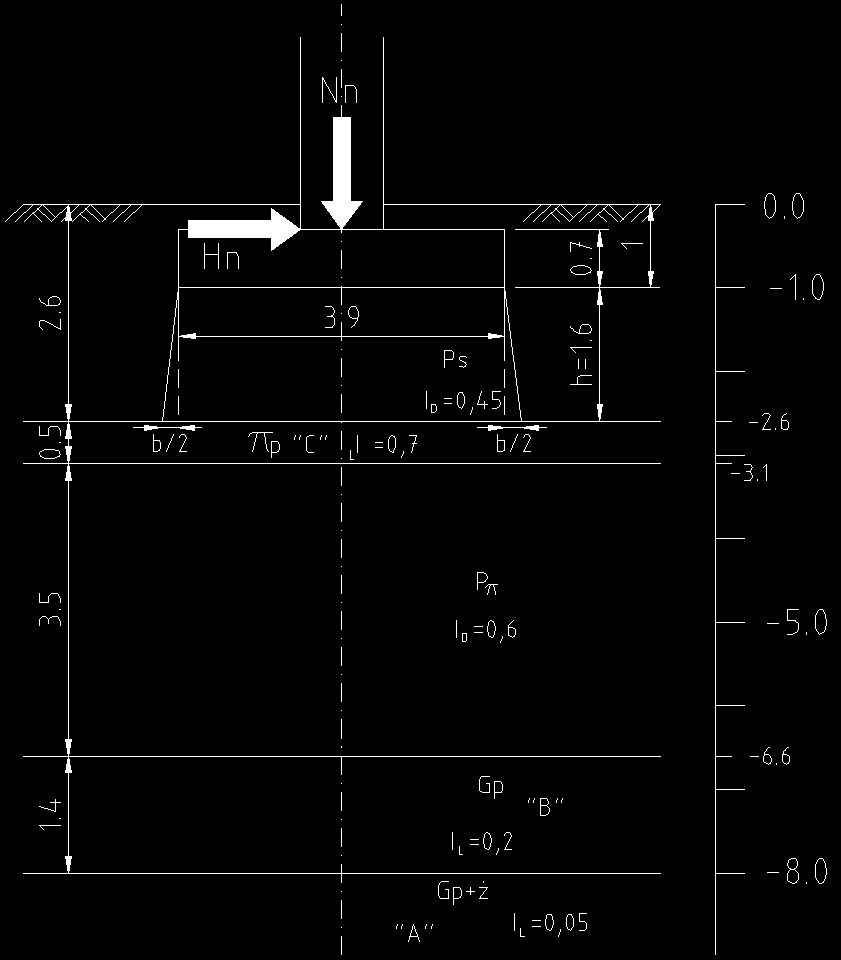
Fundament zastępczy:
B' = B + b ;
L' = L + b ;
h = 6
,
1 m ;
h < B ⇒ b = h 4 = , 0 4 m ;
B' = 9
,
3 + ,
0 4 =
m
3
,
4
;
L' = 9
,
3 + ,
0 4 =
m
3
,
4
;
D'
= 0
,
1 + 6
,
1
= 6
,
2 m ;
min
N ' = N + B'⋅ L' h
⋅ ⋅γ = 2261 5
, 4 + 3
,
4 ⋅ 3
,
4 ⋅ ,
1 6 ⋅16 6
, 5 = 2754 1
, k
1 N ;
r
r
h
Sprawdzenie, czy siła działa w rdzeniu przekroju: N ⋅ e + H ⋅ h
2261 5
, 4 ⋅ 0
,
0 28 + 75 0
, ⋅ ,
1 2 ⋅ 6
,
1
B'
e
r
B
r
' =
=
= 0
,
0 7 m
5
<
= 7
,
0 2 m ;
B
N '
2754 1
, 1
6
r
B' = B' 2
− ⋅ e' = 3
,
4 − 2 ⋅ ,
0 075 = 1
,
4 5 m ;
B
L' = L' =
m
3
,
4
;
( r )
φ
;
( r )
c
;
n
= ,
6 0 ⋅ 9
,
0
= ,
5 4
n
= 8
,
6 ⋅ 9
,
0
= 1,
6 2°
N
;
N
;
N
;
B =
0
,
0 6
D =
7
,
1 4
C =
8
,
6 5
( r )
3
γ
= 18 5
, ⋅ 9
,
0
= 16 6
, 5 kN m ;
D
−
⋅
+
⋅
r
2 ,
0 0 1 ,
0 0
5
,
0
5
,
9 7
,
3 4
( )
(
)
3
γ
=
⋅ 9
,
0
= ,
8 66 kN m ;
B
9
,
3
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 6 -
_
H
tan δ
tan ( r)
φ
;
tan δ =
r
= 0
,
0 326784 ;
= 3
,
0 05 ;
n
= 1
,
0 0722224
N '
tan ( r)
φ
r
n
i
;
i
;
i
;
B =
9
,
0 2
D =
9
,
0 7
C =
9
,
0 25
Warunek I:
q
≤ m ⋅ q ;
rs
f
m = 9
,
0 ⋅ 9
,
0
= 8
,
0 1 ;
N '
2754 1
, 1
3
q
r
=
=
= 148 9
, 5 kN m ;
rs
B'⋅ L'
3
,
4 ⋅ 3
,
4
B'
r
B'
r
B'
( )
( )
( r )
q = 1 + 3
,
0 ⋅
⋅ N ⋅ c
+ 1+ 5
,
1 ⋅
⋅ N ⋅ D' ⋅γ
+ 1− ,
0 25 ⋅
⋅ N ⋅ B'⋅γ
=
f
C
u
D
min
L'
L'
D
L'
B
B
3
,
4
3
,
4
= 1+ 3
,
0 ⋅
⋅ 8
,
6 5 ⋅ ,
5 4 + 1 + 5
,
1 ⋅
⋅ ,
1 74 ⋅ ,
2 6 ⋅1 ,
6 65 +
3
,
4
3
,
4
3
,
4
kN
+ 1− ,
0 25 ⋅
⋅ ,
0 06 ⋅ 3
,
4 ⋅ ,
8 66 = 23 ,
8 07
3
3
,
4
m
2
2
148 9
, 5 < 8
,
0 1⋅ 23 ,
8 07 ⇒ 148 9
, 5 kN m < 192 8
, 4 kN m (warunek spełniony).
Warunek II:
N ' ≤ m ⋅ Q'
;
r
fNB
m = 9
,
0 ⋅ 9
,
0
= 8
,
0 1 ;
B'
( )
'
r
B
Q'
= L'⋅ B'⋅ 1+ 3
,
0
⋅
⋅ N ⋅ i ⋅ c
+ 1+ 5
,
1
⋅
⋅ N ⋅ i ⋅ D' ⋅γ +
fNB
C
C
n
D
D
min
D
L'
L'
B'
+ 1− ,
0 25
⋅
⋅ N ⋅ i ⋅ B'⋅γ =
B
B
B
L'
1
,
4 5
1
,
4 5
= 3
,
4 ⋅ 1
,
4 5 ⋅ 1 + 3
,
0 ⋅
⋅ 8
,
6 5 ⋅ 9
,
0 25 ⋅ ,
5 4 + 1 + 5
,
1 ⋅
⋅ ,
1 74 ⋅ 9
,
0 7 ⋅ ,
2 6 ⋅1 ,
6 65 +
3
,
4
3
,
4
1
,
4 5
+ 1− ,
0 25 ⋅
⋅ ,
0 06 ⋅ 9
,
0 2 ⋅ 1
,
4 5 ⋅ ,
8 66 = 400 ,
5 6 k
1 N
3
,
4
2754 1
, 1 < 8
,
0 1⋅ 4005 6
, 1 ⇒ 2754 1
, k
1 N < 3244 5
, 4 kN (warunek spełniony)
Zatem wymiary stopy nr 1 zostały poprawnie zaprojektowane.
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 7 -
_
Stopa nr 2:
Fundament rzeczywisty:
B = 4,0 m (szerokość stopy)
L = 4,0 m (długość stopy)
D = 1,0 m (zagłębienie)
H = 0,7 m (wysokość stopy)
3
γ =
ś
2 ,
2 0 kN m
r
Warunek I:
q
≤ m ⋅ q
rs
f
m = 9
,
0 ⋅ 9
,
0
= 8
,
0 1
N + B ⋅ L ⋅ D
⋅γ
155 ,
0 0 + ,
4 0 ⋅ ,
4 0 ⋅ ,
1 0 ⋅ 2 ,
2 0
kN
n
min
q
śr
=
=
= 118 8
, 8
n
2
B ⋅ L
,
4 0 ⋅ ,
4 0
m
kN
q
= 118 8
, 8 ⋅ ,
1 2 = 14 ,
2 65
rs
2
m
B
B
B
( r )
( r )
( r )
q = 1 + 3
,
0 ⋅
⋅ N ⋅ c
+ 1+ 5
,
1 ⋅
⋅ N ⋅ D
⋅γ + 1− ,
0 25 ⋅
⋅ N ⋅ B ⋅γ
f
C
u
D
min
D
B
B
L
L
L
( r )
φ
;
n
= 3 ,
2 6 ⋅ 9
,
0
= 29 3
, 4°
( r )
c
(grunt niespoisty)
n
= ,
0 0
N
;
N
;
N
B =
8
,
6
D = 17 1
, 1
C = 2 ,
8 64
( r )
3
γ
= 18 5
, ⋅ 9
,
0
= 1 ,
6 65 kN m
D
⋅
+
⋅
+
−
⋅
+
⋅
r
18 5
,
,
1 0
2 ,
0 0 ,
1 0
20 10
,
0 75
5
,
9 7 ,
1 25
( )
(
)
3
γ
=
⋅ 9
,
0
= 1 ,
3 04 kN m
B
,
1 0 + ,
1 0 + ,
0 75 + ,
1 25
,
4 0
,
4 0
q = 1 + 3
,
0 ⋅
⋅ 2 ,
8 64 ⋅ ,
0 0 + 1 + 5
,
1 ⋅
⋅17 1
, 1⋅ ,
1 0 ⋅1 ,
6 65 +
f
,
4 0
,
4 0
,
4 0
kN
+ 1− ,
0 25 ⋅
⋅ 8
,
6 ⋅ ,
4 0 ⋅1 ,
3 04 = 97 ,
8 22
3
,
4 0
m
2
2
14 ,
2 65 < 8
,
0 1⋅ 97 ,
8 22 ⇒ 14 ,
2 65 kN m < 792 3
, 6 kN m (warunek spełniony)
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 8 -
_
Warunek II:
N ≤ m ⋅ Q
r
fNB
m = 9
,
0 ⋅ 9
,
0
= 8
,
0 1
G = N + B ⋅ L ⋅ γ
= 155 ,
0 0 + ,
4 0 ⋅ ,
4 0 ⋅ ,
1 0 ⋅ 2 ,
2 0 = 190 ,
2 0
ś
kN
n
n
r
N = ,
1 2 ⋅ G = ,
1 2 ⋅190 ,
2 0 = 228 ,
2 4 kN
r
n
Sprawdzenie, czy siła działa w rdzeniu przekroju: M = N ⋅ e ;
r
r
B
M = H ⋅ H , gdzie M = H ⋅ H
r
r
r
r
H r ⋅ H
75 0
, ⋅ ,
1 2 ⋅ 7
,
0
e
B =
=
=
B
0
,
0 28 <
= 6
,
0 7
N
228 ,
2 4
6
r
B
( )
B
r
Q
L B 1
3
,
0
N
i
c
1
5
,
1
N
i
D min γ
fNB =
⋅ +
⋅
⋅ C ⋅ C ⋅ n + + ⋅
⋅ D ⋅ D ⋅
⋅ D +
L
L
B
+ 1− ,
0 25 ⋅
⋅ N i B γ
B ⋅ B ⋅
⋅
B
L
L = L =
0
,
4 m ;
B = B − 2 ⋅ e = ,
4 0 − 2 ⋅ ,
0 028 = 9
,
3 44 m
B
H
tan δ
tan ( r)
φ
;
tan δ =
r = 0
,
0 3943218 ;
= ,
0 07 ;
n
= 5
,
0 6209217
N
tan ( r)
φ
r
n
i
;
i
;
i
;
B =
9
,
0 3
D =
9
,
0 6
C =
9
,
0 6
9
,
3 44
9
,
3 44
Q
= ,
4 0 ⋅ 9
,
3 44 ⋅ 1 + 3
,
0 ⋅
⋅ 2 ,
8 64 ⋅ 9
,
0 6 ⋅ ,
0 0 + 1 + 5
,
1 ⋅
⋅17 1
, 1⋅ 9
,
0 6 ⋅ ,
1 0 ⋅1 ,
6 65 +
fNB
,
4 0
,
4 0
9
,
3 44
+ 1− ,
0 25 ⋅
⋅ 8
,
6 ⋅ 9
,
0 3 ⋅ 9
,
3 44 ⋅1 ,
3 04 = 14561 9
,
k
1 N
,
4 0
228 ,
2 4 < 8
,
0 1⋅14561 9
, 1 ⇒ 228 ,
2 4 kN < 11795 1
,
k
5 N (warunek spełniony)
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 9 -
_
Fundament zastępczy:
B' = B + b ;
L' = L + b ;
h = ,
1 0 m ;
h < B ⇒ b = h 4 = , 0 2 m
5
B' = ,
4 0 + ,
0 25 = ,
4 25 m ;
L' = ,
4 0 + ,
0 25 = ,
4 25 m ;
D'
= 0
,
1 + 0
,
1
= 0
,
2 m
min
N ' = N + B'⋅ L' h
⋅ ⋅γ = 228 ,
2 4 + ,
4 25 ⋅ ,
4 25 ⋅ ,
1 0 ⋅1 ,
6 65 = 2583 1
, 4 kN
r
r
h
Sprawdzenie, czy siła działa w rdzeniu przekroju: N ⋅ e + H ⋅ h
228 ,
2 4 ⋅ 0
,
0 28 + 75 0
, ⋅ ,
1 2 ⋅ 0
,
1
B'
e
r
B
r
' =
=
= 0
,
0 6 m <
= 7
,
0
m
1
B
N '
2583 1
, 4
6
r
B' = B' 2
− ⋅ e' = ,
4 25 − 2 ⋅ ,
0 06 = 1
,
4
m
3
;
B
L' = L' = ,
4 2 m
5
;
( r )
φ
;
( r )
c
;
n
= ,
6 0 ⋅ 9
,
0
= ,
5 4
n
= 8
,
6 ⋅ 9
,
0
= 1
,
6 2°
N
;
N
;
N
B =
0
,
0 6
D =
7
,
1 4
C =
8
,
6 5
( r )
3
γ
= 18 5
, ⋅ 9
,
0
= 16 6
, 5 kN m
D
⋅
+
−
⋅
+
⋅
+
⋅
r
2 ,
0 0 ,
1 0
2 ,
0 0 1 ,
0 0
,
0 75
5
,
9 7 ,
1 25
2 ,
2 0 ,
1 0
( )
(
)
3
γ
=
⋅ 9
,
0
= 13 8
, 3 kN m
B
,
4 0
H
tan δ
tan ( r)
φ
;
tan δ =
r
= 0
,
0 348413 ;
= 3
,
0 25 ;
n
= 1
,
0 0722224
N '
tan ( r)
φ
r
n
i
;
i
;
i
;
B =
9
,
0 2
D =
9
,
0 7
C =
9
,
0 3
Warunek I:
q
≤ m ⋅ q
rs
f
m = 9
,
0 ⋅ 9
,
0
= 8
,
0 1 ;
N '
2583 1
, 4
3
q
r
=
=
= 14 ,
3 01 kN m ;
rs
B'⋅ L'
,
4 25 ⋅ ,
4 25
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 10 -
_
B'
r
B'
r
B'
( )
( )
( r )
q = 1 + 3
,
0 ⋅
⋅ N ⋅ c
+ 1+ 5
,
1 ⋅
⋅ N ⋅ D' ⋅γ
+ 1− ,
0 25 ⋅
⋅ N ⋅ B'⋅γ
=
f
C
u
D
min
L'
L'
D
L'
B
B
,
4 25
,
4 25
= 1+ 3
,
0 ⋅
⋅ 8
,
6 5 ⋅ ,
5 4 + 1 + 5
,
1 ⋅
⋅ ,
1 74 ⋅ ,
2 0 ⋅1 ,
6 65 +
,
4 25
,
4 25
,
4 25
kN
+ 1− ,
0 25 ⋅
⋅ ,
0 06 ⋅ ,
4 25 ⋅13 8
, 3 = 195 5
, 9
3
,
4 25
m
2
2
14 ,
3 01 < 8
,
0 1⋅195 5
, 9 ⇒ 148 9
, 5 kN m < 15 ,
8 43 kN m (warunek spełniony)
Warunek II:
N ' ≤ m ⋅ Q'
;
r
fNB
m = 9
,
0 ⋅ 9
,
0
= 8
,
0 1 ;
B'
( )
'
r
B
Q'
= L'⋅ B'⋅ 1+ 3
,
0
⋅
⋅ N ⋅ i ⋅ c
+ 1+ 5
,
1
⋅
⋅ N ⋅ i ⋅ D' ⋅γ +
fNB
C
C
n
D
D
min
D
L'
L'
B'
+ 1− ,
0 25
⋅
⋅ N ⋅ i ⋅ B'⋅γ =
B
B
B
L'
1
,
4 3
1
,
4 3
= ,
4 25 ⋅ 1
,
4 3 ⋅ 1 + 3
,
0 ⋅
⋅ 8
,
6 5 ⋅ 9
,
0 3 ⋅ ,
5 4 + 1 + 5
,
1 ⋅
⋅ ,
1 74 ⋅ 9
,
0 7 ⋅ ,
2 0 ⋅1 ,
6 65 +
,
4 25
,
4 25
1
,
4 3
+ 1− ,
0 25 ⋅
⋅ ,
0 06 ⋅ 9
,
0 2 ⋅ 1
,
4 3 ⋅13 8
, 3 = 324 ,
6 25 kN
,
4 25
2583 1
, 4 < 8
,
0 1⋅ 324 ,
6 25 ⇒ 2583 1
, 4 kN < 262 ,
9 46 kN (warunek spełniony)
Zatem wymiary stopy nr 2 zostały poprawnie zaprojektowane.
II STAN GRANICZNY (OSIADANIE):
STOPA NR 1.
N + G
1550 + 9
,
3 ⋅ 9
,
3 ⋅ ,
1 0 ⋅ 2 ,
2 0
n
2
q
n
=
=
= 123 9
, 1 kN m
n
B ⋅ L
9
,
3 ⋅ 9
,
3
2
σ γ = σ = γ ⋅ D = 18 5,⋅ 0
,
1
= 18 5
, kN m
0
0 s
Ps
2
σ = q −σ γ = 123 9,1−18 5, = 10 ,541 kN m 0 d
n
0
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 11 -
_
L : B = 9
,
3 : 9
,
3
= ,
1 0
σ = σ
0
⋅η
zs
s
S
σ = σ
0
⋅η
zd
d
S
( i)
( i)
σ ⋅ h
s '
zd
=
i
( i )
M 0
( i)
( i)
σ ⋅ h
s "
zs
= λ ⋅
i
( i )
M
s = s '+ s "
i
i
z
= 3
,
4
m
3
max
Sprawdzam osiadanie dla 7 warstw (do głębokości 5,7 m): Osiadanie w fazie eksploatacji: s(1)=0,14035 cm Dopuszczalne osiadanie dla hal przemysłowych: 5,0 cm.
Zatem 0,14035 cm < 5,0 cm
STOPA NR 2.
N + G
1550 + ,
4 0 ⋅ ,
4 0 ⋅ ,
1 0 ⋅ 2 ,
2 0
n
2
q
n
=
=
= 118 8
, 8 kN m
n
B ⋅ L
,
4 0 ⋅ ,
4 0
2
σ γ = σ = γ ⋅ D = 18 5,⋅ 0
,
1
= 18 5
, kN m
0
0 s
Ps
2
σ = q −σ γ = 118 8,8 −18 5, = 100 3,8 kN m 0 d
n
0
L : B = ,
4 0 : ,
4 0 = ,
1 0
z
= 9
,
3 2 m
max
Sprawdzam osiadanie dla 6 warstw (do głębokości 4,75 m): Osiadanie w fazie eksploatacji: s(2)=0,51643 cm Dopuszczalne osiadanie dla hal przemysłowych: 5,0 cm.
Zatem 0,51643 cm < 5,0 cm
s
∆ = s(2) − s )1( = 5
,
0 1643 − 1
,
0 4035 = 3
,
0 760 c
8 m
∆ s
3
,
0 7608
=
cm = ,0000215 < ,003 (gdzie R to odległość między osiami fundamentów) R
175 ,
0 0 cm
Zatem osiadania, które wystąpią w fazie eksploatacji, zawierają się w dopuszczalnych, umownych wartościach zgodnie z normą PN-81/B-03020.
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 12 -
_
KOMENTARZ I OCENA WYKONANYCH OBLICZEŃ:
1. Charakterystyka warunków gruntowo – wodnych.
W podłożu występują złożone warunki gruntowo-wodne co jest uwarunkowane różnorodnością gruntów zalegających pod fundamentami.
- Stopa fundamentowa nr 1 posadowiona jest w piasku średnim o ID=0,45, którego głębokość sięga do 2,6 m. Kolejnymi warstwami są: pył piaszczysty o IL=0,7 i grubości 0,5 m; piasek pylasty o ID=0,6 i grubości 3,5 m; glina piaszczysta o IL=0,2 i grubości 1,4 m oraz grupie genetycznej „B”; glina piaszczysta ze żwirem o IL=0,05 i nieokreślonej grubości oraz grupie genetycznej „A”. Warstwą słabą jest pył piaszczysty.
Ciśnienie spływowe występuje na całej grubości warstwy pyłu piaszczystego, zatem poziom ustabilizowany wody jest na głębokości 2,6 m, natomiast poziom nawiercony wody na 3,1 m.
- Stopa fundamentowa nr 2 również posadowiona jest w piasku średnim o ID=0,45, którego głębokość sięga do 2,0 m. Kolejnymi warstwami są: pył piaszczysty o IL=0,7 i grubości 1,75 m; piasek pylasty o ID=0,6 i grubości 1,25 m; glina piaszczysta o IL=0,2 i grubości 3,0 m oraz grupie genetycznej „B”; glina piaszczysta ze żwirem o IL=0,05 i nieokreślonej grubości oraz grupie genetycznej „A”. Warstwą słabą również jest pył piaszczysty.
Ciśnienie spływowe występuje tylko na części grubości warstwy pyłu piaszczystego, zatem poziom ustabilizowany wody jest na głębokości 3,0 m, natomiast poziom nawiercony wody na 3,75 m.
2. Opis i ocena nośności podłoża.
Przeprowadzone obliczenia wykazały, że fundamenty o następujących wymiarach:
- stopa 1: 3,9x3,9 m
- stopa 2: 4,0x4,0 m
spełnią normowy warunek, co przedstawiają powyższe obliczenia.
3. Omówienie osiadań.
Wyliczone osiadania całkowite dla stóp odpowiednio 1 i 2 wyszły: 0,71914 cm oraz 1,35495 cm. W fazie eksploatacji (oraz po uwzględnieniu zmax): 0,14035 cm oraz 0,51643 cm. Stosunek róznicy osiadań i odległością między osiami fundamentów spełnia normowy warunek i wynosi: ∆ s R =
0
,
0 00215 <
0
,
0 3 .
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 14 -
_
STOPA NR 1.
Naprężenia w
y
]
Moduły
Osiadanie
Osiadanie
Rodzaj i
ść
[ m
środku warstw
o
y
[ kPa]
z
z
[ cm]
w fazie
arstw
stan
b
η
[ kN/m2]
ru
[ m]
S
B
eksploatacji
r w
gruntu
G
arstw
σ
σ
N
M
s'
s''
s
[c m]
w
0
M
zd
zs
Ps
1
0,8
0,4
0,1
0,93
98,03
17,21
0,08714
0,01377
0,10091
-
ID=0,45
90000,0
100000,0
Ps
2
0,8
1,2
0,31
0,68
71,68
12,58
0,06372
0,01006
0,07378
-
ID=0,45
πp „C”
3
0,5
11000,0
18333,33 1,85
0,47
0,53
55,87
9,81
0,25395
0,02675
0,28070
0,14035
IL=0,7
Pπ
4
0,9
2,55
0,65
0,43
45,33
7,96
0,05589
0,00785
0,06374
-
ID=0,6
Pπ
5
0,9
3,45
0,88
0,32
33,73
5,92
0,04158
0,00584
0,04742
-
ID=0,6
73000,0
91250,0
Pπ
6
0,9
4,35
1,12
0,25
26,35
4,63
0,03249
0,00457
0,03706
-
ID=0,6
Pπ
7
0,9
4,8
1,35
0,18
18,97
3,33
0,02339
0,00328
0,02667
-
ID=0,6
Gp „B”
8
0,7
6,05
1,55
0,15
15,81
2,78
0,02991
0,00394
0,03385
0,01693
IL=0,2
37000,0
49333,33
Gp „B”
9
0,7
6,75
1,73
0,12
12,65
2,22
0,02393
0,00315
0,02708
0,01354
IL=0,2
Gp+ż „A”
10
0,8
7,5
1,92
0,11
11,60
2,04
0,01326
0,00210
0,01536
0,00768
IL=0,05
70000,0
77777,78
Gp+ż „A”
11
0,8
8,3
2,13
0,09
9,49
1,67
0,01085
0,00172
0,01257
0,00629
IL=0,05
0,71914
0,18479
_ _
Daniel Sworek gr. B8
Ćwiczenie projektowe z fundamentowania nr2
- 16 -
_
STOPA NR 2.
y
]
Naprężenia w
Moduły
Osiadanie
Osiadani
ść
[ m
środku warstw
e w fazie
Rodzaj i
o
y
[ kPa]
z
z
[ cm]
arstw
b
η
[ kN/m2]
eksploat
stan gruntu
ru
[ m]
S
B
r w
G
arstw
acji
σ
σ
N
M
s'
s''
s
w
0
M
zd
zs
[c m]
Ps
1
1,0
90000,0
100000,0
0,5
0,125
0,87
87,33
16,00
0,09703
0,01600
0,11303
-
ID=0,45
πp „C”
2
0,9
1,45
0,363
0,63
63,24
11,66
0,51742
0,05724
0,57466
0,28733
IL=0,7
11000,0
18333,33
πp „C”
3
0,85
2,325
0,581
0,47
47,18
8,70
0,36457
0,04034
0,40491
0,20246
IL=0,7
Pπ
4
0,65
3,075
0,769
0,36
36,14
6,66
0,03218
0,00474
0,03692
-
ID=0,6
73000,0
91250,0
Pπ
5
0,6
3,7
0,925
0,3
30,11
5,55
0,02475
0,00365
0,02840
-
ID=0,6
Gp „B”
6
0,75
4,375
1,094
0,23
23,09
4,26
0,04680
0,00648
0,05328
0,02664
IL=0,2
Gp „B”
7
0,75
5,125
1,281
0,2
20,08
3,7
0,04070
0,00563
0,04633
0,02317
IL=0,2
37000,0
49333,33
Gp „B”
8
0,75
5,875
1,469
0,16
16,06
2,96
0,03255
0,00450
0,03705
0,01853
IL=0,2
Gp „B”
9
0,75
6,625
1,656
0,14
14,05
2,59
0,02848
0,00394
0,03242
0,01621
IL=0,2
Gp+ż „A”
10
0,75
7,375
1,844
0,12
12,05
2,22
0,01291
0,00214
0,01505
0,00753
IL=0,05
70000,0
77777,78
Gp+ż „A”
11
0,75
8,125
2,031
0,1
10,04
1,85
0,01076
0,00178
0,01254
0,00627
IL=0,05
1,35495
0,58814
_ _
Daniel Sworek gr. B8