Synteza regulatora cyfrowego - model we/wy obiektu.

REALIZOWANE CELE:

• Zbadanie, w środowisku programowym Matlab/Simulink, rezultatów syntezy regulatora cyfrowego dla obiektu o znanej transmitancji dyskretnej przy zastosowaniu wybranych metod projektowania. W trakcie ćwiczeń są badane:

• układy regulacji projektowane przy orientacji na lokalizację ich biegunów (ang. PPC: pole placement controller, PZPC: pole - zero placement controller).

• układy regulacji projektowane na podstawie modelu zakłóceń losowych przy udziale regulatora minimalnowariancyjnego (ang. MVC: minimum variance controller) - z założenia dysponujemy wówczas modelem parametrycznym odzwierciedlającym właściwości probabilistyczne oddziaływujących zakłóceń.

W trakcie badań symulacyjnych przeprowadzana jest również optymalizacja parametrów regulatora w strukturze PID w układzie stabilizacji wielkości wyjściowej przy silnych zakłóceniach losowych

• Wszechstronny program badań układu regulacji w trakcie którego wylicza się szereg najczęściej stosowanych wskaźników jakości sterowania. Przeprowadzenie na tym tle porównawczej oceny układów regulacji z zastosowaniem reguł optymalizacji wielokryterialnej.

Z założenia, ćwiczenia realizowane są przy komputerze z programem Matlaba w wersji 4.2 (lub wyżej) sprzężonym z językiem symulacyjnym Simulink i pakietem programowym Control.

PRZED ĆWICZENIAMI:

• Należy powtórzyć materiał teoretyczny na temat przekształcania transmitancji liniowego obiektu dynamicznego na transmitancje dyskretną (przy zadanym czasie próbkowania).

Pytania kontrolne. Jakie główne metody uproszczeń są przy tym przekształceniu stosowane? W jakich wersjach uproszczeń możemy zrealizować przekształcanie tego typu w środowisku programowym Matlaba? W jaki sposób uwzględnia się przy transformacji opóźnienie w obiekcie sterowania? Przedstaw zalecenia na temat wyboru czasu próbkowania w układzie regulacji?

• Przed ćwiczeniem na temat regulatorów ustalających położenie (PPC, PZPC) miejsc zerowe wielomianów układu regulacji, należy powtórzyć materiał na temat ich syntezy. Treść zestawień A i B zamieszczonych w dalszej części opracowania traktujemy przy tym jako plan powtórzenia.

Pytania kontrolne. Przedstaw związki między położeniem biegunów układu regulacji i jego własnościami. W jaki sposób uzyskujemy równanie diofantyczne dla układów z tymi regulatorami? Czy rozwiązanie tego równania jest jednoznaczne? Gdzie znajdują się zera układu sterowania z regulatorem PPC?

• Przed ćwiczeniem na temat regulatorów minimalnowariancyjnych MVC należy powtórzyć, przy pomocy zestawienia C, materiał teoretyczny na temat modelowania obiektów znajdujących się pod wpływem silnych zakłóceń o charakterze stochastycznym i syntezy układów regulacji pracujących w tych warunkach.

Pytania kontrolne. Jakie modele obiektów stochastycznych są najczęściej stosowane? Jakiego typu model jest najprostszym? Wymień własności modelu ARMAX (CARMA)? W jakich sytuacjach regulacja minimalnowariancyjna stanowi potencjalnie najbardziej racjonalne rozwiązanie problemu? Wymień istotne wady regulacji tego typu. W jaki sposób możemy je osłabić?

• Przed zadaniem optymalizacji układu regulacji w strukturze PID należy przypomnieć, stosowane w poprzedniej serii ćwiczeń, metody optymalizacji statycznej. Inne, istotniejsze problemy teoretyczne o tematyce związanej z tym zadaniem zgrupowano w zestawieniu D, w dalszej części opracowania.

METODYKA I PROGRAMOWANIE BADAŃ:

Obiekt sterowania w ćwiczeniach jest wyjściowo ustalany za pośrednictwem transmitancji Laplace'a. Model ten należy następnie przekształcić, po uprzednim ustaleniu czasu próbkowania T, do modelu dyskretnego. Przekształcenie to możemy przeprowadzić automatycznie, dokładnie lub metodą przybliżoną, w wyniku realizacji krótkiego programu. Przedstawimy przykład w którym obiekt sterowania jest podwójnym członem inercyjnym ze stałymi czasowymi T1=2s, T2=5 i czasem opóźnienia T0=2s.

Bc = 1; Ac = [10, 7, 1]; % wielomiany transmitancji obiektu:

[ac,bc,c,dd]= tf2ss(Bc,Ac), % model ciągły w postaci zmiennych stanu

% Załóżmy, że za czas próbkowania przyjęto 1s. Otrzymamy wówczas:

[ad,bd] = c2d (ac,bc,1); % dyskretne wersje macierzy stanu i sterowań

[B,A] = ss2tf(ad,bd,c,dd), % wielomiany transmitancji dyskretnej obiektu.

% Zgodność przeprowadzonych działań sprawdzimy na wykresie:

step(Bc,Ac), hold on

dstep(B,A), hold off,

pause, % Po naciśnięciu dowolnego klawisza - cd. programu

% Znormalizujemy wielomian licznika ( cel: niezerowy najstarszy

% współczynnik) zastępując zera odpowiednim opóźnieniem wynikowym:

nb=length(B); na=length(A); d=0;

for i=1:nb,

if B(i)<eps, d=d+1; B=B(2:length(B)); else break; end;

end;

nb=length(B);

d=d+2; % Wprowadzenie opóźnienia 2 taktów.

% Z założenia w torze zakłóceń umieścimy także filtr C/A, gdzie:

C = [1 -.7], nc=length(C);

Równolegle wprowadzana jest tu transmitancja filtru szumu białego w torze zakłóceń kształtująca stochastyczny model addytywnego sygnału zakłócającego na wyjściu obiektu. Podkreślmy, że wśród bloków standartowych Simulinka istnieje w grupie extrcont blok „S domain to Z domain” realizujący analogiczną transformację automatycznie.

Synteza regulatora wiąże się z konstrukcją m-funkcji Matlaba pozwalającą automatycznie skonstruować i rozwiązać odpowiadające wymaganiom równanie wielomianowe. Przedstawimy przykłady programów tego typu rozpoczynając od regulatora cyfrowego lokalizującego bieguny (ang. PPC - pole placement controller) wynikowego układu regulacji.

function [S,R,H] = ppc (A, B, C, bieguny, d);

% Funkcja wylicza wielomiany S, T i R dyskretnego regulatora dla obiektu

% A*y(t) = z^(-d)*B*u(t) + C*e(t);

% umiejscawiającego bieguny wynikowego układu regulacji w "bieguny".

if nargin<5, d=0; else B =[zeros(1,d),B]; end; % uwz. opóźnienia

p = length(A)-1; q =length(B)-1;

T = poly(bieguny); CT = conv(C,T); r=length(CT)-1;

% Rozwiążemy równanie Diofantesa: TC=AF+z^(-d)BG metodą Wołgina [ ]:

if r < p + q, % to otrzymujemy układ (p+q) równań.

% Macierz znanych współczynników w tym układzie:

M=zeros(p+q);

for k=1:q, M(k,k:(k+p))=A; end

for k=q+1:p+q, M(k,k-q:k)=B; end

% wektor prawej strony natomiast:

N = [CT, zeros(1,p+q-length(CT))];

% Rozwiązanie układu równań:

w = N*inv(M);

% należy podzielić na dwie części:

F = w(1:q); G = w(q+1:p+q);

else % otrzymujemy układ (r+1) równań

% z macierzą znanych współczynników:

M=zeros(r+1);

for k=1:1+r-p, M(k,k:(k+p))=A; end

for k=r-p+1:r+1, M(k,k-r+p:k-r+p+q)=B; end

% wektor prawej strony natomiast:

N = CT;

% Rozwiązanie układu równań:

w=N*inv(M);

% należy podzielić na dwie części:

F=w(1:r-p+1); G = w(r-p+2:r+1);

end;

S = G; R = F;

T=((polyval(conv(A,R),1)+polyval(conv(B,S),1))/polyval(B,1))*C;

Równanie uzyskiwanego regulatora przyjmuje postać:

R(z^-1)u(t) = T(z^-1)w(t)-S(z^-1)y(t);

wiążąc oddziaływanie u(t) na obiekt sterowany z pomiarami jego wyjścia y(t) i sygnałem zadającym w(t). Po wywołaniu m-funkcji „ppc” z odpowiednim zestawem argumentów następuje automatyczne wyliczenie współczynników w równaniu różnicowym regulatora. Np., po wprowadzeniu do przestrzeni roboczej Matlaba wektorów A,B,C wielomianów transmitancji dyskretnej sterowanego obiektu i opóźnienia d, wywołując:

[S,R,T] = ppc(A,B,C,[0.5,0.1],d);

otrzymujemy bezpośrednio wielomiany regulatora ustalającego bieguny zamkniętego układu regulacji w punktach: 0,5 i 0,1. Program wyliczający wielomiany licznika i mianownika regulatora minimalnowariancyjnego (ang. MVC- minimal variance controller)może być znacznie prostszy ze względu na istniejącą tu możliwość zastąpienia procesu rozwiązywania układu równań standardową m-funkcją: deconv. Funkcja ta oblicza wynik i resztę z dzielenia dwu wielomianów.

function [LR,MR] = mvc (A, B, C, d)

% Funkcja wylicza wielomiany licznika (LR) i mianownika (MR)

% regulatora minimalnowariancyjnego dla obiektu typu CARMA:

% A*y(t) = z^(-d)*B*u(t) + C*e(t);

if nargin<4, d=0; end; nc=length(C); na=length(A);

if nc < na + d -1, Coblicz = [C,zeros(1,na - nc + d-1)];

else Coblicz = C;

end;

% Z równania definiującego: C = AF + G*z^(-d);

[F,G0] = deconv( Coblicz, A );

MR = conv (B, F); ng=length(G0); k=0;

for i=1:ng,

if abs(G0(i))<.000001, k=k+1; else break, end;

end;

LR = G0(k+1:ng); nl = length(LR); k=0;

for i=1:nl,

if abs(LR(nl-i+1))<.00000000001, k=k+1; else break, end;

end; LR = LR(1: nl-k);

Z założenia zaprojektowany układ z regulatorem MVC realizuje zadanie stabilizacji wielkości regulowanej. Równanie uzyskiwanego regulatora:

u(t) = - LR(z^-1)y(t)/ MR(z^-1);

w którym LR(z^-1), MR(z^-1)są wielomianami zmiennej z^-1, wiąże wartość aktualnego oddziaływania u(t) na obiekt sterowany z aktualnymi wektorami pomiarów jego wyjścia i sterowań.

Badania symulacyjne układu regulacji z zaprojektowanym regulatorem przeprowadzamy programując obliczenia bezpośrednio w Matlabie, lub w środowisku języka symulacyjnego Simulinka. W formie przykładu przedstawimy zwięzły program realizujący obliczenia ukierunkowane na analizę własności uzyskanego układu regulacji..

[S,R,T]= dpp (A,B,C,bieguny,d), % wylicza wielomiany regulatora;

zS = roots(S), zR = roots(R), zT = roots(T), % zera odp.wielomianów;

nlr=length(S); nmr=length(R); dstep(S,R),

pause, % Po obejrzeniu wykresu naciśnij dowolny klawisz

% Połączenie regulatora z obiektem --------------------------------------

Ls=conv(T,B); Lz=[zeros(1,d),Ls]; % Licznik transmitancji układu regulacji

M1=conv(R,A); M2=[zeros(1,d),conv(B,S)];

n1=length(M1); n2=length(M2);

if n1>n2, Mz = M1 + [M2, zeros(1,n1-n2)];

else if n2>n1 Mz = M2 + [M1, zeros(1,n2-n1)];

else Mz = M1+ M2;

end; % Mz = Mianownik transmitancji układu regulacji

end

roots(Mz), % sprawdzamy położenie biegunów i zer układu wynikowego

ys= filter(Lz,Mz,ones(1,30)); plot(ys,'b'), hold on,% i jego ch-kę skokową;

pause, % Po naciśnięciu dowolnego klawisza - cd programu

Lu = conv(A,T); % licznik transmitancji U(z)/W(z) implikuje

% przebieg w tym czasie przebieg na wyjściu regulatora w postaci:

us= filter(Lu,Mz,ones(1,30)); plot(us,'r'), hold off

pause, % Po naciśnięciu dowolnego klawisza - cd programu

PROGRAM ĆW.7. Układ regulacji z ustaleniem jego biegunów (i zer).

1. Wybierz czas próbkowania w układzie regulacji realizującym sterowanie otrzymanym (transmitancja) obiektem, a następnie wyznacz jego transmitancje dyskretną.

2. Przeprowadź program badań ukierunkowany na ilustratywny przegląd podstawowych własności regulatora i uzyskiwanego układu regulacji przy zastosowaniu określonej taktyki wyboru położenia biegunów układu zamkniętego.

Wskazówka 1. Przez „podstawowe własności” należy rozumieć tu zarówno oceny jakościowe przebiegów u(t), y(t) przy typowych (np. skokowe, lub liniowe przestawienie) zmianach wartości zadanej w układzie, jak i ścisłe oceny ilościowe wyliczane na podstawie ustalonych wskaźników, np. wartość niektórych wskaźników integralnych związanych z „odpracowaniem” skutków skokowego zakłócenia. Badamy tu własności trzech - czterech typów układów regulacji, np. „układu szybkiego”, uzyskiwanego w wyniku wybór biegunów rzeczywistych z przedziału: 0 - 0,2; układu z biegunem rzeczywistym z przedziału: 0,85 - 0,95; układu z parą biegunów dominujących typu zespolonego, itp.

Wskazówka 2. Typowy etap programu badań składa się z następujących przedsięwzięć:

Etap 1. Wybierane są bieguny (i ewentualnie zera) badanego układu regulacji.

Etap 2. Obliczane są współczynniki równania różnicowego (tj. wielomiany) regulatora.

Etap 3. Odtwarzana jest (automatycznie - działając w Matlabie) transmitancja układu zamkniętego z tym regulatorem. Równorzędną formą rozwiązania zadania jest zamodelowanie układu w środowisku Simulinka.

Etap 4. Generowane są sygnały oddziaływujące na badany układ i przedstawiany jest, graficznie i w postaci wskaźników ilościowych, rezultat obliczeń (modelowania) zgodny z tematem doświadczenia.

3. W uzupełnieniu programu badań z poprzedniego punktu należy porównać odporność wynikowego układu regulacji na zmiany jednego z parametrów (stała czasowa, opóźnienie, lub współczynnik wzmocnienia) sterowanego obiektu. W tym celu, przy ustalonym regulatorze, zmieniamy badany parametr w przedziale + 50% odnotowując, z podkreśleniem zmian, własności symulowanych układów regulacji. Jaki wskaźnik można zaproponować do kompleksowej oceny odporności układu?

SPRAWOZDANIE POWINNO ZAWIERAĆ teksty programów, lub schematy blokowe układów stosowanych w trakcie badań, przedstawione w miarę możliwości w postaci graficznej wyniki przeprowadzonych badań symulacyjnych, a także wypowiedzi na temat:

• związku uzyskiwanych współczynników sprzężeń zwrotnych z lokalizacją biegunów wynikowego układu regulacji (na podstawie p.2 programu ćwiczenia),

• odporności otrzymywanego układu regulacji na zmiany własności sterowanego obiektu (p.3 ćwiczenia).

PROGRAM ĆW.8. Układ regulacji minimalnowariancyjnej i optymalizacji doboru parametrów regulatora PID dla obiektu działającego na tle silnych zakłóceń stochastycznych.

1. Uzupełnij model sterowanego obiektu z poprzedniego ćwiczenia o tor zakłóceń. W trakcie badań w ćwiczeniu posługujemy się modelem obiektu typu ARMAX (CARMA) z zadanym zbiorem wielomianów C(z^-1):

A(z^-1)y(t) = B(z^-1)u(t-d)-C(z^-1)ε(t).

2. W uzupełnieniu programu badań z poprzedniego ćwiczenia, prowadzonego na tle sygnałów deterministycznych, oceniamy jakościowo ( porównanie przebiegów wielkości zakłócającej i regulowanej przy ustalonej wartości zadanej) zdolność "odpracowywania" przez regulator addytywnych zakłóceń probabilistycznych na wyjściu sterowanego obiektu. Stosujemy przy tym jeden z regulatorów PPC wybrany spośród uzyskanych w trakcie poprzednich badań. Jakie wniosek implikuje wynik tego doświadczenia?

Wskazówka. Przebieg wielkości regulowanej możemy uzyskać za pośrednictwem transmitancji zakłóceniowo - wyjściowej: G_z(z^-1 ) = Y(z^-1 )/Z(z^-1 ); badanego układu regulacji. Tekst odpowiedniego fragmentu programu może wyglądać następująco:

Lzy=conv(R,A); % Licznik transmitancji Z(s)/Y(s):

z=filter(C,A,randn(1,100)); figure(2), plot(z), hold on

yz=filter(Lzy,Mz,z); plot(yz,'b'), hold off

3. Przeprowadź badania symulacyjne ukierunkowane na zbadanie efektu zmniejszenia wariancji wielkości wyjściowej przy zastosowaniu reguł regulacji minimalnowariancyjnej σ_yMV² ( w nieregulowanym obiekcie wynosi ona σ_y² ). Badania przeprowadzamy dla określonego zbioru modeli addytywnych sygnałów zakłócających definiowanych przy pomocy wielomianu C(z^-1). W trakcie badań wyznaczamy również wariancję oddziaływania sterującego σ_u² stanowiącą swoisty wskaźnik „kosztu sterowania minimalnowariancyjnego”. Jakie jest położenie biegunów uzyskiwanych w trakcie obliczeń układów regulacji? Jakiego rzędu są równania uzyskiwanych regulatorów? Czy uzyskiwany poziom wskaźnika regulacyjności zależy od własności oddziaływujących zakłóceń?

Wskazówka. W trakcie badań, do każdej wersji modelu zakłóceń (model toru sterowania obiektu jest ustalony), dobieramy odpowiedni regulator minimalnowariancyjny. Następnie, po zarejestrowaniu przebiegów, m.in. odnotowujemy uzyskiwany wskaźnik regulacyjności:

r_o = (σ_y^{2 -} σ_yMV² ) / σ_y².

4. Sprawdź wyrywkowo, w dwu - trzech sytuacjach (dla różnych wielomianów C_i(z^-1) z poprzedniego programu badań), na ile możemy zbliżyć się do osiąganych tam rezultatów jakościowych przy zastosowaniu mechanizmu optymalizacji parametrów regulatora w ramach struktury PID. Na ile bliskie są, przy jednakowych własnościach obiektów sterowania, parametry uzyskiwanego regulatora PID parametrom regulatora typu MVC?

Wskazówka. W celu sprawdzenia optymalizujemy ( patrz program ćwiczeń poprzedniego rozdziału) parametry regulatora PID orientując się na minimalizację sumy kwadratów błędów regulacji w ciągu określonej liczby taktów pracy systemu.

5. Należy sprawdzić odporność jednego ( np. charakteryzującego się największą regulacyjnością) z układów regulacji badanych w p.3 ćwiczenia na zwiększenie opóźnienia w równaniu sterowanego obiektu o jeden takt. Czy układ zachowuje stabilność? Czy wariancja wielkości wyjściowej rośnie istotnie?

SPRAWOZDANIE POWINNO ZAWIERAĆ oprócz stosowanych programów, schematów blokowych i uzyskanych wyników przeprowadzonych badań symulacyjnych odpowiedzi na wszystkie pytania przedstawione drukiem pochyłym w sformułowaniach zadań badawczych w ćwiczeniu.

Zestawienie A.

Modele obiektów dynamicznych (wejście/wyjście).

Ogólna postać modelu liniowego dyskretnego procesu dynamicznego wyraża się za pośrednictwem wielomianów określających własności torów oddziaływań kontrolowanych i zakłócających:

A(z^-1)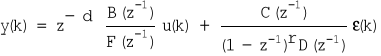
.

Jest to najbardziej ogólne wyrażenie struktury modelu. Przez ε(k) oznaczono tu realizacje białego szumu z zerowym matematycznym oczekiwaniem: E{ε(k)}=0; i funkcją autokorelacji w postaci: R_εε(τ)= σ_ε² δ(τ). W modelu występują wielomiany zmiennej zespolonej z^-1: A(z^-1),B(z^-1),C(z^-1),D(z^-1),F(z^-1), np.

A(z^-1) = a₀+a₁z^-1+ a₂z^-2 + ...+ a_nA z^-nA; jest wielomianem stopnia nA.

Wyraz wolny wielomianu A(z^-1)ustalany jest z reguły na poziomie: a₀=1.Inne wielomiany możemy przedstawić analogicznym wyrażeniem oznaczając ich stopnie odpowiednio poprzez: nB, nC, nD. Pozostałe oznaczenia: r - rząd różnicowania w opisie niestacjonarnego ciągu czasowego zakłóceń (typ ARIMA), d - opóźnienie w torze sterowania. Stosowane podczas syntezy sterowania modele dynamicznych obiektów liniowych powstają w wyniku upraszczania tej struktury najogólniejszej. Przypomnijmy najważniejsze z nich:

Model ARX (ang. AutoRegressive with eXogenous variable):

;

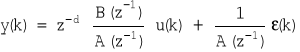
jest najprostszą ze stosowanych wersji modelu parametrycznego dla obiektów dynamicznych. Zwróćmy uwagę na automatyczne przyjmowanie, w wyniku zastosowania danej struktury, arbitralnego założenia o autoregresyjnym modelu AR ciągu addytywnych zakłóceń z(k) na wyjściu badanego obiektu. Umiejscawiany w torze zakłóceń filtr szumu białego ε(k) jest tu ściśle powiązany z transmitancją toru sterowania za pośrednictwem wspólnego wielomianu A(z^-1):

A(z^-1)z(k)= ε(k).

W związku z równoważnością zależności definiującej model ARX z równaniem różnicowym:

A(z^-1)y(k) = B(z^-1)u(k-d) + ε(k);

istnieje tu możliwość bezpośredniego zastosowania estymatora najmniejszych kwadratów (MNK) do estymacji współczynników występujących w nim wielomianów. Równanie to możemy bowiem zapisać w formie wyrażającej wielkość wyjściową obiektu jako liniową kombinację:

yest(k)= ϕ(k-1) c + ε(k);

wejściowych zmiennych regresyjnych w postaci:

ϕ(k-1) = [-y(k-1), ... ,-y(k-nA), u(k-d), ... ,u(k-d-nB)].

Wektor estymowanych parametrów w tej sytuacji jest równy (symbolem (.)^T oznaczono transpozycję):

c = [a₁, a₂,...,a_nA, b₀ , b₁,..., b_nB]^T .

W trakcie estymacji stosuje się często technikę obliczeń związaną ze zmienną instrumentalną (ang. IV - instrumental variable). Najprostsza interpretacja zmiennej instrumentalnej związana jest z zastąpieniem w macierzy doświadczenia U modelu ARX wyników pomiarów wyjścia y(i) wynikami jego estymacji z modelu, tj. ν(i) = yest(k).

Stosuje się struktury modelu z mniej arbitralnym opisem własności toru zakłóceń niż ujmuje to model ARX. Wymienimy kilka z nich w kolejności związanej z rosnącą złożonością modelu sygnału zakłócającego (AR, MA, ARMA), a tym samym według rosnących trudności obliczeniowych przy rozwiązywaniu zadania estymacji parametrów liniowego filtru białego szumu w torze zakłóceń.

Model ARARX (ang. AutoRegressive, AutoRegressive with eXogenous variable):

.

powstaje w wyniku uogólnienia modelu AR oddziaływujących zakłóceń. Model ten możemy wyrazić również poprzez dwa równania różnicowe :

A(z^-1) y(k) = B(z^-1) u(k-d) + v(k);

D(z^-1) v(k) = ε(k).

Identyfikacja obiektu w związku z tym może być przeprowadzana dwustopniowo. W pierwszej fazie obliczeń, metodą zmiennej instrumentalnej, otrzymuje się ocenę współczynników wielomianów charakteryzujących dynamikę toru sterowania A(z^-1) i B(z^-1). Następnie, po wyliczeniu szeregu czasowego błędów równania obiektu (tj. ocen realizacji zakłóceń vest(k) ) następuje identyfikacja jego modelu w strukturze AR, co jest równoważne z oszacowaniem współczynników wielomianu D(z^-1). Postępowanie tego typu jest określane jako uogólnienie MNK.

Model ARMAX (ang. AutoRegressive Moving Average with eXogenous variable):

A(z^-1) y(k) = B(z^-1) u(k-d) + C(z^-1) ε(k);

jest modelem związanym z ważoną średnią ostatnich (nC+1) realizacji białego szumu ε(k). Należy podkreślić, że zera wielomianu odwrotnego do C(z^-1):

C*(z) = C(z^-1) z^nC = z^nC + c₁ z^nC-1 + ... + c_nC ;

powinny leżeć wewnątrz koła jednostkowego.

Struktura modelu w tej postaci jest bardzo popularną, zalecaną w literaturze, formą modelowania procesu dynamicznego. Estymacja parametrów jest tu, obliczeniowo, trudniejsza niż w modelu poprzednim, ze względu na nieliniową zależność wskaźnika jakości identyfikacji od estymowanych parametrów c_i. Wynika to z wyrażenia uogólnionego błędu równania obiektu w postaci:

[ A(z^-1) y(k) - B(z^-1) u(k-d)].

W procesie oceny występujących w równaniu parametrów stosuje się tu algorytmy iteracyjne minimalizacji funkcji wielu zmiennych. Minimalizowany jest przy tym wskaźnik jakości identyfikacji wynikający z metody największej wiarygodności NW (ang. ML - Maximum Likelihood).

Model BJ (model Boxa-Jenkinsa):

;

stanowi bardzo ogólny model parametryczny formułowany dla stacjonarnego procesu dynamicznego, swobodnie, za pośrednictwem modelu ARMA opisując właściwości zakłóceń oddziaływujących na badany, sterowany od strony wejścia u(k) proces dynamiczny.

Za podstawę estymacji współczynników może posłużyć tu metoda błędu predykcji ε(k):

ε(k) = (D(z^-1)/C(z^-1))(y(k) - (B(z^-1)/A(z^-1))u(k-d));

polegająca na zastosowaniu jednego z algorytmów iteracyjnych optymalizacji ( np. metoda Newtona - Raphsona) do minimalizacji wskaźnika:

Pakiet Identyfikacji Matlaba zawiera funkcję „bj.m”, przy pomocy której możemy (posiadając serię pomiarów wejść i wyjść identyfikowanego obiektu) zrealizować to postępowanie automatycznie.

Modele liniowych obiektów wielowymiarowych tworzy się poprzez kombinacje liniowe poszczególnych r torów prowadzących do danego wyjścia. Mieszczą się więc one w klasie opisywanej równaniem:

A(z^-1)y(k)= B₁(z^-1)u(k-d₁)/F₁(z^-1)+...+B_r(z^-1)u_r(k-d_r)/F_r(z^-1)+

+ C(z^-1)ε(k)/D(z)

Podkreślmy, że w zasadzie istotna jest tu liczba wejść - przy wielu wyjściach i jednym wejściu mamy do czynienia z kilkoma równolegle rozpatrywanymi modelami pojedynczego wymiaru SISO (ang. Single Input Single Output ).

Modele nieliniowe formułuje się, ogólnie rzecz biorąc, w torze sterowania obiektu, pozostawiając model liniowy w torze zakłóceń. Deterministyczna część prawej strony wyjściowego nieliniowego równania różnicowego:

y(k) = f ( u(k), u(k-1) , ..., u(k-n) );

zastępowana jest z reguły wielomianem niewysokiego ( tj. drugiego lub trzeciego stopnia) od kolejnych wyrazów ciągu sterowań. Równanie uproszczone uzyskuje się poprzez pozostawienie pierwszych wyrazów rozwinięcia Taylora występującej w tym równaniu funkcji nieliniowej wielu zmiennych: f(.). W wyniku otrzymuje się, np.:

;

tj. model liniowy względem parametrów, lecz kwadratowy względem wejść systemu.

Klasę modeli liniowych względem parametrów, lecz nieliniowych względem wejść, nazywa się modelami Hammersteina. Charakterystyczna cecha liniowości względem parametrów w tych modelach pozwala na ich transformację i w następstwie stosowanie przy analizie metod przeznaczonych do analizy układów liniowych. Np. w modelu Hammersteina o strukturze:

A(z^-1)y(k)= B₁(z^-1)u(k) + B₂(z^-1)u²(k)+...+ B_m(z^-1)u^m(k) + ε(k),

po przyjęciu sztucznego sygnału wejściowego w postaci:

ϕ(k) = [ u(k), u²(k), ... , u^m(k)]^T;

otrzymujemy model pseudo-liniowy i pseudo-wielowymiarowy o m zdefiniowanych wejściach.

Zestawienie B.

Równania wybranych regulatorów cyfrowych.

Ogólna postać równania dyskretnego regulatora dla liniowego procesu dynamicznego wyraża się za pośrednictwem trzech wielomianów : S(z^-1), T(z^-1), R(z^-1) jednoznacznie określających związek między wielkościami: zadaną w(k), regulowaną y(k) i sterującą u(k):

R(z^-1) u(k) = T(z^-1) w(k) - S(z^-1) y(k).

R(z^-1), S(z^-1), T(z^-1) nazywane są w związku z tym wielomianami regulatora.

Będziemy stosować oznaczenia:

R(z^-1) = R = r₀+r₁z^-1+ r₂z^-2 + ...+ r_nR z^-nR; jest wielomianem stopnia nR,

S(z^-1) = S = s₀+s₁z^-1+ s₂z^-2 + ...+ s_nS z^-nS; jest wielomianem stopnia nS.

T(z^-1) = T = t₀+t₁z^-1+ t₂z^-2 + ...+ t_nA z^-nT; jest wielomianem stopnia nT.

Zadanie syntezy regulatora cyfrowego polega na wyznaczeniu równania regulatora (wielomianów R, S, T) dla zadanego obiektu sterowania. Zwykle wyznacza się je za pośrednictwem wielomianów pomocniczych ( oznaczanych w zestawieniu poprzez F(z^-1), G(z^-1)) uzyskiwanych w rezultacie rozwiązania wielomianowego równania diofantycznego. Równanie diofantyczne otrzymujemy w rezultacie sekwencji przekształceń natury algebraicznej powstającej w wyniku ścisłego sformułowania celu sterowania na tle równań obiektu i regulatora, a następnie rozwiązania wynikających stąd równań układu regulacji.

W dalszej części zestawienia przedstawimy stosunkowo często formułowane cele regulacji cyfrowej, wynikające stąd równania diofantyczne i wyrażenia określające wielomiany regulatora. Występujące w tych równaniach wielomiany A(z^-1),B(z^-1),C(z^-1),a także liczba d pochodzą z modelu dynamiki obiektu sterowania (poprzednie zestawienie).

Regulacja z ustalonym położeniem biegunów układu związana jest z zapewnieniem otrzymania wynikowego równania systemu sterowania w postaci:

y(k) = K* B(z^-1)z^-d w(k)/ A*(z^-1).

A*(z^-1) jest tu pożądanym, formułowany a'priori wielomianem charakterystycznym, a przez K* oznaczono współczynnik ustalający jednostkowe wzmocnienie obwodu zamkniętego ( K* = A*(1)/B(1)). W literaturze ten sposób regulacji określany jest jako PP (ang. Pole Placement), a odpowiednie regulatory przez PPC (ang. Pole Placement Controller).

Zauważmy, w związku deterministycznym charakterem rozpatrywanego modelu obiektu, że regulacja tego typu stosowana jest raczej w tych sytuacjach, w których zadaniem podstawowym jest możliwie szybkie, dokładne „odpracowanie” zmian wartości zadanej, natomiast oddziaływujące zakłócenia o charakterze probabilistycznym nie są zbyt istotne. Sytuacja tego typu zachodzi np. w wielu serwomechanizmach.

Sposób rozwiązania zadania PP regulacji wynika bezpośrednio z przekształceń algebraicznych. Z równania obiektu:

A(z^-1) y(k) = B(z^-1) u(k-d);

i przedstawionego wyżej równania regulatora otrzymuje się transmitancję wynikowego układu regulacji w postaci:

G(k)= [z^-d B(z^-1)T(z^-1)]/[ A(z^-1)R(z^-1)+z^-d B(z^-1)S(z^-1)] .

Po przyrównaniu mianownika tej transmitancji do wielomianu wynikającego z celu stawianego w zadaniu: widocznym jest, że wielomiany R(z^-1),S(z^-1) występujące w regulatora PP można uzyskać w wyniku rozwiązania równania wielomianowego:

A(z^-1)R(z^-1)+z^-d B(z^-1)S(z^-1)= A^*(z^-1)A_pom(z^-1);

Obecność z prawej strony równania stabilnego wielomianu pomocniczego A_pom(z^-1) wynika z celowości wprowadzenia stopni swobody na ewentualny wybór postaci trzeciego wielomianu z równania regulatora:

T(z^-1) = A_pom(z^-1)K^*.

Stopnie nR, nS wielomianów uzyskiwanych z rozwiązywania równania diofantycznego określa się następująco:

nR = d - 1 +nB; nS = max {nA-1, nA_pom(z^-1)+nA^*-d-nB}.

Zauważmy, że wielomian mianownika transmitancji sterowanego obiektu A(z^-1) zostaje w rezultacie skompensowany (a więc wyjściowo może być niestabilnym) w wyniku uzyskiwanej reguły generowania sterowania obiektem, wielomian licznika natomiast B(z^-1) pozostaje w transmitancji układu wynikowego. Z założenia oba wielomiany powinny nie zawierać wspólnego czynnika ( tj. być względnie pierwszymi).

Przy stosowaniu metodyki PP obowiązkiem projektanta jest ustalenie racjonalnej lokalizacji zbioru biegunów {z_i[A*]} układu regulacji. Patrząc ze strony jakości uzyskiwanego układu regulacji, problem ten nie jest skomplikowany ze względu na wyraźne związki składowych czasowych przebiegów przejściowych s_i(k) z położeniem biegunów. Składowe te, w układzie stabilnym (bieguny w kole jednostkowym |z_i|<1), mają charakter przebiegów wykładniczo gasnących. Ściśle rzecz ujmując:

s_i(k) = C_i z_i^k ; dla biegunów rzeczywistych (gdzie: C_i -stałe);

s_i(k) = C_i re(z_i)^k sin(im(z_i)k); dla biegunów zespolonych sprzężonych.

Odpowiedź na skok wartości zadanej, minimalnej liczbie taktów możemy uzyskać umiejscawiając wszystkie bieguny projektowanego układu regulacji w początku układu współrzędnych. Układy z taką cechą nazywane są w literaturze jako układy ze skończoną odpowiedzią impulsową (SOI), a sposób regulacji jako DB (ang. dead beat control). Z drugiej strony jednak, zapewnienie szybkości przebiegów może być okupione koniecznością stosowania zbyt dużych, będących nie do przyjęcia w praktyce, oddziaływań sterujących.

W regulacji z ustalonym położeniem zer i biegunów za cel stawia się uzyskanie wynikowego transmitancji układu dynamicznego w postaci:

G*(z^-1) = B*(z^-1)z^-d / A*(z^-1).

Oba wielomiany: A*(z^-1) i B*(z^-1) są tu ustalane przez projektanta. Zadanie tego rodzaju formułuje się dla obiektów minimalnofazowych ze stabilnym wielomianem licznika B(z^-1). W literaturze oznaczane jest ono jako PZP1 (ang. Pole-Zero Placement).

Rozwiązanie zadania PZP1 regulacji sprowadza się, podobnie jak poprzednio rozważane zadanie PP regulacji, do rozwiązania równania wielomianowego. W związku z koniecznością zapewnienia podzielności wynikowego wielomianu mianownika A*(z^-1)przez wielomian B(z^-1) postać tego równania jest jednak nieco inną. Po znalezieniu wielomianów pomocniczych : F(z^-1),G(z^-1), z równania diofantycznego:

A(z^-1)F(z^-1)+z^-d G(z^-1)= A^*(z^-1)A_pom(z^-1);

można określić wielomiany regulatora PZPC:

R(z^-1)=B(z^-1)F(z^-1); S(z^-1)=G(z^-1); T(z^-1)= B^*(z^-1)A_pom(z^-1);

W zadaniach typu PZP1 projektant może zadać swobodnie wzorcowy model układu regulacji, w przypadku sterowania obiektem nieminimalnofazowym natomiast (zadanie PZP2) możliwości kształtowania są ograniczone. Wśród zaleceń na dobór modelu odniesienia można wymienić wielomiany Grahama i Lathropa [3], którzy otrzymali transmitancje wzorcowe minimalizując kryterium całkowe IMTE (granica w nieskończoności całki z iloczynu modułu uchybu regulacji i czasu w zadaniu przestawienia) dla ciągłych dynamicznych układów liniowych różnych rzędów.

W literaturze (np. [2] ) rozpatruje się także wiele modyfikacji zadań regulacji PP i PZP związanych z wprowadzeniem dodatkowych ograniczeń, lub celów sterowania np. w postaci docelowego usunięcia wpływu zakłóceń o charakterze deterministycznym, lub minimalizacji wpływu zakłóceń o charakterze probabilistycznym. Formułowane są również zasady syntezy wielomianów regulatorów adaptacyjnych w zadaniu lokalizacji biegunów, lub zer i biegunów wynikowego układu regulacji.

Wyróżniana jest między innymi wersja tego zadania ( PZP2 ) przeznaczona dla obiektów nieminimalnofazowych. W wersji tej, w równaniu układu regulacji:

y(k) = B^-(z^-1)B*(z^-1)z^-d w(k)/ A*(z^-1),

musi pozostać w liczniku niestabilny, a w związku z tym nie podlegający kompensacji (dlaczego?), składnik wielomianowy B^-(z^-1) w liczniku transmitancji obiektu sterowania.

Otrzymuje się wówczas równanie Diophantesa w postaci:

A(z^-1)F(z^-1)+z^-d B^-(z^-1)G(z^-1)= A^*(z^-1)A_pom(z^-1);

a wielomiany regulatora określa się na podstawie ich związków z wielomianami F(z^-1), G(z^-1) stanowiącymi jego rozwiązanie:

R(z^-1)=B⁺(z^-1)F(z^-1); S(z^-1)=G(z^-1); T(z^-1)= B^*(z^-1)A_pom(z^-1).

Regulacja minimalnowariancyjna jest formułowana dla obiektów modelowanych stochastycznie (np. model w strukturze ARMAX) w dwu wersjach:

• W wersji prostej celem jest generowanie ciągu sterowań u(k) minimalizującego wariancji wielkości regulowanej :

min E { y²(k+d)}.

• W wersji ważonej celem generowanego ciągu sterowań u(k)jest minimalizacja liniowej kombinacji ( współczynnik ważący r) wariancji wielkości regulowanej i sterującej:

min E { y²(k+d) + r u²(k)}.

W literaturze ten sposób regulacji i realizujące je regulatory określane są jako MVC (ang. Minimum Variance Control i Minimum Variance Controller).

Regulacja tego typu stosowana jest w tych układach stabilizacji wielkości zadanej, w których problem podstawowym jest obecność modelowanych np. przy pomocy wielomianu C(z^-1)w modelu CARMA zakłóceń stochastycznych. Sytuacja tego typu może zachodzić np. w układach wytłumiania silnych przypadkowych drgań (pojazdy, taśmociągi, itp).

Rozwiązanie zadania regulacji MV związane jest możliwości kompensacji tych zaburzeń wielkości regulowanej, które wynikają z zakłóceń wygenerowanych przez otoczenie sterowanego procesu w przedziale czasowym sprzed taktu o numerze (k-d)- przypomnijmy, że k określa moment aktualny, d natomiast reprezentuje opóźnienie w równaniu obiektu. Przedstawimy zarys tego rozwiązania.

Z równania obiektu typu ARMAX (zakładamy stabilność wielomianów A,B) wynika, że:

y(k+d) = B u(k)/A + C ε(k+d)/A.

Wprowadzimy wielomiany pomocnicze: F(z^-1)=1+f₁z^-1+f₂z^-2+...+f_d-1z^-(d-1);

G(z^-1)=g₀+g₁z^-1+g₂z^-2+...+g_nG z^-nG;

spełniające równanie diofantyczne z prawą stroną równą wielomianowi C określającemu model zakłóceń (stopień wielomianu G jest tu równy : nG = max{nA-1, nC-d} ):

A(z^-1)F(z^-1)+z^-d G(z^-1)= C(z^-1).

Możemy wówczas, po kilku przekształceniach algebraicznych, wyrazić wielkość regulowaną równaniem zmodyfikowanym w postaci:

y(k+d)=[B(z^-1)F(z^-1)u(k)/C(z^-1)+G(z^-1)y(k)/C(z^-1)] + F(z^-1)ε(k+d);

w której wyraźnie widoczny jest, ujęty w nawiasy kwadratowe, składnik określający predykcję tej wielkości (oznaczaną przez y_P(k+d|k)) na moment czasowy (k+d) wyrażaną przy pomocy danych posiadanych w momencie k. W momencie k-tym nie możemy znać bowiem wartości przyszłych realizacji zakłóceń ε(k+i) i w związku z tym realizacji wartości zmiennej losowej wyrażanej przez:

F(z^-1)ε(k+d) = ε(k+d) + f₁ ε(k+d-1) +...+ f_d-1 ε(k+1);

Wiemy jedynie, że matematyczne oczekiwanie tej zmiennej ma wartość zerową. Zero jest więc jednocześnie najlepszą predykcją wartości tego wyrażenia na przyszłość. Celem regulacji minimalnowariancyjnej jest minimalizacja wyrażenia E{y²(k+d)}.Optymalną wartość tego wyrażenia uzyskamy przy wyzerowaniu predykcji y_P(k+d|k), tj. wspomnianego składnika w nawiasach kwadratowych. Prowadzi to do prawa sterowania w postaci:

u(k)= - G(z^-1)y(k)/ B(z^-1)F(z^-1);

i w związku z tym wielomianów regulatora: R(z^-1)= B(z^-1)F(z^-1);

S(z^-1)= G(z^-1); G(z^-1)=0;

Wartość minimalizowanej wariancji wskazuje na graniczne możliwości wytłumiania zakłóceń w ramach regulacji minimalnowariancyjnej:

E{y²(k+d)} = σ² (1 + f₁² +...+ f_d-1² ).

Obok regulacji minimalnowariancyjnej prostej, związanej z minimalizacją wariancji wyjścia układu regulacji stosowana jest czasem nieco inna zasada sterowania (regulator typu GMVC, tj. ang. general minimal variance controller)) oparta na regule minimalizacji wskaźnika zbudowanego na sumie ważonej wariancji wyjścia i wariancji sterowania. Optymalizacja tego typu może zapewnić racjonalny kompromis między jakością sterowania, a jego kosztem.

Należy podkreślić, że zarówno regulatory, jak i własności układów regulacji uzyskiwane w wyniku rozwiązania zadania GMVC różnią się istotnie od uzyskiwanych w rezultacie stosowania metody MVC. Metodyka projektowania obu regulatorów jest natomiast zbliżona. Główna różnica formalna związana jest z koniecznością wprowadzenia (przy zastosowaniu metody uogólnionej) poprawki do równania Diophantesa [ ].

---