Odsetki proste.

gdzie:
- kapitał końcowy,

- kapitał początkowy,

- stopa procentowa (roczna) [%].

Po dwóch latach mamy:

Po trzech latach mamy:

Po
latach mamy:

Jeśli w roku jest
okresów oprocentowania, a czas trwania lokaty obejmuje
okresów to:

Oczywiście można wyznaczyć jaki powinien być kapitał początkowy:

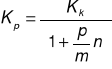
Można również wyznaczyć ilość okresów oprocentowania, po których kapitał początkowy osiągnie określoną wartość:

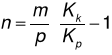
Procent składany.

Kapitał + odsetki biorą udział w wyznaczaniu odsetek dla kolejnego okresu.

gdzie:
- liczba lat utrzymywania lokaty.

Jeśli w roku mamy
okresów kapitalizacji to dla jednego roku utrzymywania lokaty mamy:

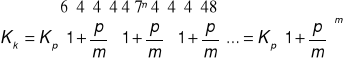
Jeśli w roku mamy
okresów kapitalizacji to dla
okresów utrzymywania lokaty mamy:

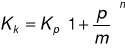
W celu obliczenia przyszłej wartości kapitału dla oprocentowania składanego można posłużyć się funkcją FV (Future Value).

Funkcja FV oblicza przyszłą wartość lokaty przy założeniu stałych płatności (spłata), danej wartości początkowej (pv) i stałej stopie procentowej (stopa).

Składnia: FV(Stopa ; Npr ; Spłata ; Wartość_aktualna ; Typ)

Stopa stopa procentowa stała w okresie spłaty.

Npr jest łączną liczbą okresów płatności i kapitalizacji (liczba lat).

Spłata jest wpłatą dokonywaną okresowo, nie ulega zmianie w czasie trwania kredytu. Rata obejmuje zazwyczaj kapitał i odsetki z wyłączeniem innych opłat i podatków.

Wartość_aktualna określa kapitał początkowy. Może to być przykładowo wielkość lokaty. Jeśli argument ten zostanie pominięty, domyślnie przyjmuje się wartość 0.

Typ jest liczbą 0 lub 1 i wskazuje kiedy przypada płatność (0 - koniec okresu, 1 - początek okresu)

Dla naszego przykładu 1.1.2 mamy:

FV(E4; E6; 0; E2; 0)

gdzie:

E4 - adres komórki ze stopą procentową dla okresu (u nas dla roku),

E6 - adres komórki z liczbą okresów utrzymywania kapitału,

Spłata=0 ponieważ my nic nie spłacamy,

E2 - adres komórki z kapitałem początkowym,

Typ=0 ponieważ zakładamy, że odsetki są dopisywane na koniec okresu.

W celu obliczenia niezbędnego kapitału początkowego dla uzyskania określonego kapitału końcowego można posłużyć się funkcją PV.

Funkcja PV pozwala, obok funkcji FV, PMT, NPER, RATE na rozwiązanie tzw. Równania Bankierów, które jest połączeniem zagadnienia rachunku rentowego i procentu składanego. Funkcja PV pozwala obliczyć wartość bieżącą szeregu płatności (spłata) oraz opcjonalnie obliczyć wartość bieżącą przyszłej wartości (fv).

Składnia: PV(Stopa ; Lpr ; Spłata ; Fv ; Typ )

Stopa jest stopą procentową stałą we wszystkich okresach; na przykład, jeśli uzyskano pożyczkę na samochód na 10% rocznie i dokonano miesięcznych spłat, to miesięczna stopa procentowa wynosi 10%/12, czyli 0,83%. Do formuły jako stopa można wprowadzić 10%/12 lub 0,83% albo 0,0083.

Npr jest liczbą płatności oraz kapitalizacji lokaty; na przykład, jeśli otrzymano czteroletnią pożyczkę i dokonano miesięcznych spłat, to pożyczka ma 4*12 (lub 48) okresów. Można wprowadzić 48 do formuły jako npr.

Spłata jest to płatność dokonywana w każdym okresie i nie może być zmieniana w ciągu całej spłaty pożyczki. Zwykle spłata zawiera kapitał i odsetki bez innych opłat czy podatków; na przykład miesięczne spłaty czteroletniej pożyczki wynoszącej 10 000 zł oprocentowanej na 12% rocznie wynoszą 263,33 zł. Jako spłatę wprowadza się do formuły wartość -263,33.

Fv jest wartością końcową lub poziomem finansowym, jaki chce się uzyskać po ostatniej spłacie. Jeśli fv i spłata są różnych znaków to wartości nawzajem się znoszą. Jeżeli argument jest pominięty, to jako jego wartość przyjmuje się 0 (przyszła wartość pożyczki na przykład wynosi 0). Na przykład, jeśli chce się zaoszczędzić 50 000 zł w ciągu 18 lat na określony cel, to 50 000 zł jest wartością przyszłą.

Typ to liczba 0 lub 1 wskazująca, kiedy płatność ma miejsce (0 - koniec okresu, 1- początek okresu)

Parametr Fv jest kwotą jaką chce się uzyskać (kapitał końcowy).

1

2

---