Sprawozdanie z wykonania ćwiczenia nr 401.

TEMAT : WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA ŚWIATŁA ZA POMOCĄ REFRAKTOMETRU ABBEGO.
IMIĘ I NAZWISKO : SEBASTIAN GOS
WYDZIAŁ : Elektryczny	SEMESTR : zimowy	ROK AKADEMICKI : 1999/2000
ZESPÓŁ : nr 7	DATA WYKONANIA : 15 listopad 1999
OCENA :	PODPIS :

Na granicy dwóch ośrodków izotropowych
i
, w których światło rozchodzi się z różnymi prędkościami
i
, promień świetlny wchodzący z ośrodka
do ośrodka
zmienia kierunek swojego biegu. Jeżeli np. wiązkę promieni świetlnych skierujemy z powietrza na powierzchnię wody , wówczas część promieni świetlnych ulegnie odbiciu , a część wejdzie do wody , tworząc tzw. wiązkę załamaną. Doświadczalnie stwierdzono , że jeżeli ośrodek
jest optycznie rzadszy od ośrodka 2, wówczas kąt załamania jest mniejszy od kąta padania oraz
. Gdy zaś o środek
jest optycznie gęstszy od ośrodka 2 , promień załamuje się od prostopadłej i wówczas
oraz
.

Stałą wartość stosunku sinusów kątów padania i załamania), równą stosunkowi prędkości rozchodzenia się światła w ośrodkach
i
, nazywamy współczynnikiem załamania ośrodka
względem ośrodka
i oznaczamy przez
.

Obok współczynnika załamania światła charakterystyczną wielkością każdego ośrodka jest jego dyspersja optyczna. Miarą dyspersji danego ośrodka jest różnica współczynników załamania dla linii F i C Fraunhofera , przy czym linia F leży w krótkofalowej części widma , linia C w długofalowej :

Zdolność łamiącą danego ośrodka charakteryzuje współczynnik załamania
dla żółtej linii Fraunhofera
. Stosunek :

naywano zdolnością rozszczepiającą względną danego ośrodka. Pomiar kąta granicznego może być wykorzystany do wyznaczania współczynnika załamania. Jeżeli mierzymy kąt graniczny
przy przechodzeniu światła z ośrodka badanego o nieznanym współczynniku załamania
do ośrodka o współczynniku znanym
, to szukany współczynnik

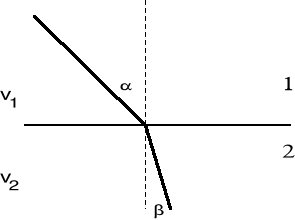
Rys.1.Załamanie światła na pograniczu dwu ośrodków:
. Promień padający , załamany i normalny do granicy ośrodków wystawiona w punkcie padania, leżą w jednej płaszczyźnie. Stosunek sinusa kąta padania do sinusa kąta załamania równy jest stosunkowi prędkości fazowej
światła w ośrodku pierwszym do prędkości fazowej
światła w ośrodku drugim.

TABELA 1

NUMER POMIARU
	1	2	3
1	1,3345	1,3344	1,33445	1,33445
2	1,425	1,425	1,425	1,425
3	1,337	1,3365	1,3365	1,3366
4	1,363	1,363	1,363	1,363
5	1,447	1,447	1,447	1,447

TABELA 2

NUMER POMIARU
	1	2	3					10^-3
1	43,5	43	43,5	43,33	1,33445	0,02473	0,03225	4,444
2	44	44,5	44,5	44,33	1,425	0,02437	0,03004	4,273
3	43,5	43,5	43	43,33	1,3366	0,02473	0,03225	4,444
4	43,5	43,5	44	43,66	1,363	0,02459	0,03165	4,682
5	43,5	43,5	44	43,66	1,447	0,02431	0,02938	5,829

WNIOSKI:

Dokładność pomiarów zależy przede wszystkim od czystości powierzchni pryzmatu. Należy uważać, aby po każdym pomiarze powierzchnię dokładnie oczyścić, osuszyć i nie poryzować powierzchni pryzmatu. Przyczyną błędów jest również niedokładność ustawienia linii granicznej na skrzyżowaniu nici pajęczych. Obraz nici powinien być bardzo ostry, ułatwi to dokładne ustawienie.

---