Sprawozdanie z wykonania ćwiczenia nr 515.

TEMAT : BADANIE CHARAKTERYSTYKI LICZNIKA GEIGERA-MÜLLERA
IMIĘ I NAZWISKO : SEBASTIAN GOS
WYDZIAŁ : Elektryczny	SEMESTR : zimowy	ROK AKADEMICKI : 1999/2000
ZESPÓŁ : nr 7	DATA WYKONANIA : 10 styczeń 2000
OCENA :	PODPIS :

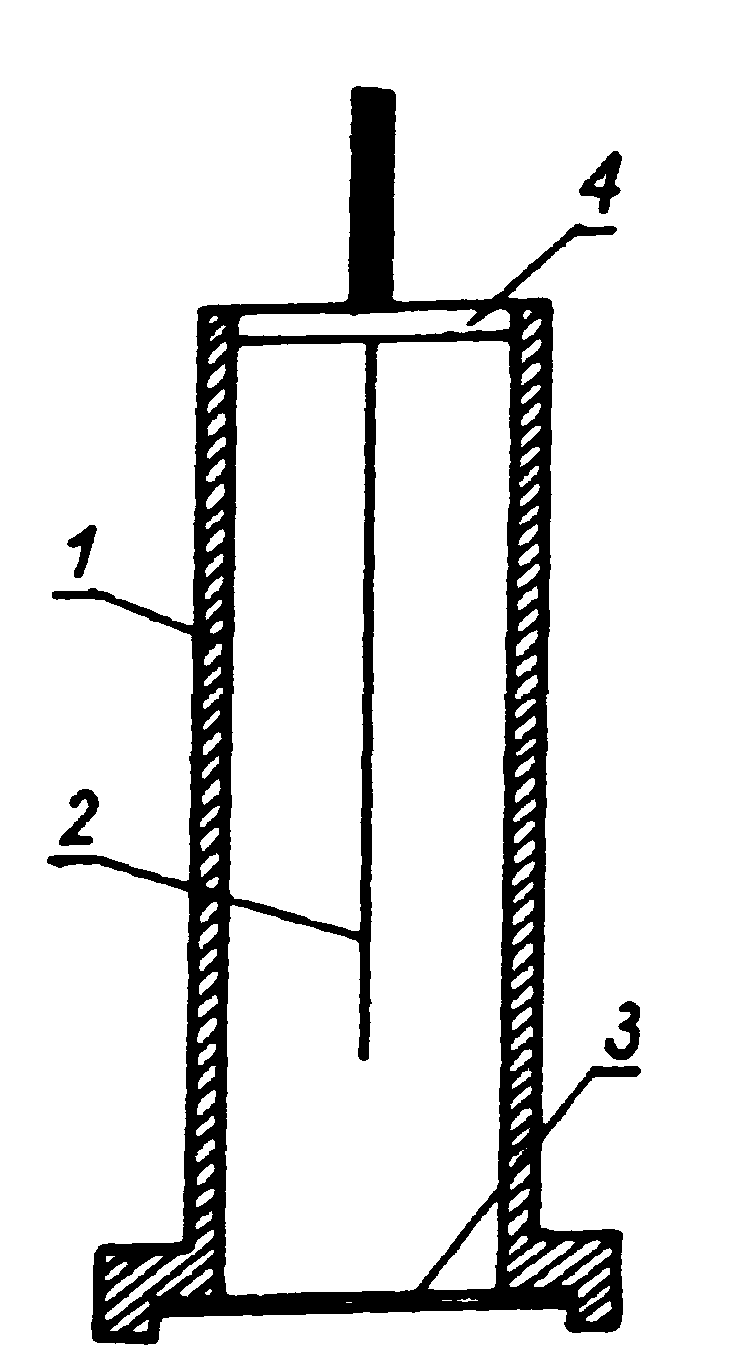
Licznik Geigera-Mullera składa się z cylindrycznej katody i anody w postaci nici metalowej przeciągniętej wzdłuż osi cylindra. Katoda jest odizolowana od anody dielektrykiem o dobrych własnościach izolujących. Przestrzeń między elektrodami wypełniona jest gazem rozrzedzonym. Gazem tym jest zwykle argon z domieszką par alkoholu (przy licznikach chlorowcowych w skład gazu wypełniającego wchodzi brom). Liczniki przeznaczone do pomiaru cząstek muszą mieć cienki ścianki, aby cząstki te mogły przedostać się do środka licznika (do jego objętości czynnej). Licznik, którego katoda wykonana jest z aluminium o grubości 0,1mm nie przepuszcza do swego wnętrza około 30% cząstek promieniowania o maksymalnej energii widma 2MeV. Aby usunąć to pochłanianie cząstek w ściankach, buduje się liczniki, które mają w swych katodach okienka osłonięte cienką folią. Jednym z tego rodzaju rozwiązań konstrukcyjnych jest licznik Geigera-Mullera okienkowo-ostrzowy użyty w naszym ćwiczeniu (rys.1). Okienko w tym liczniku jest wykonane z miki o grubości 2,7 ± 0,3 mg/cm². Katoda zbudowana jest z mosiądzu.

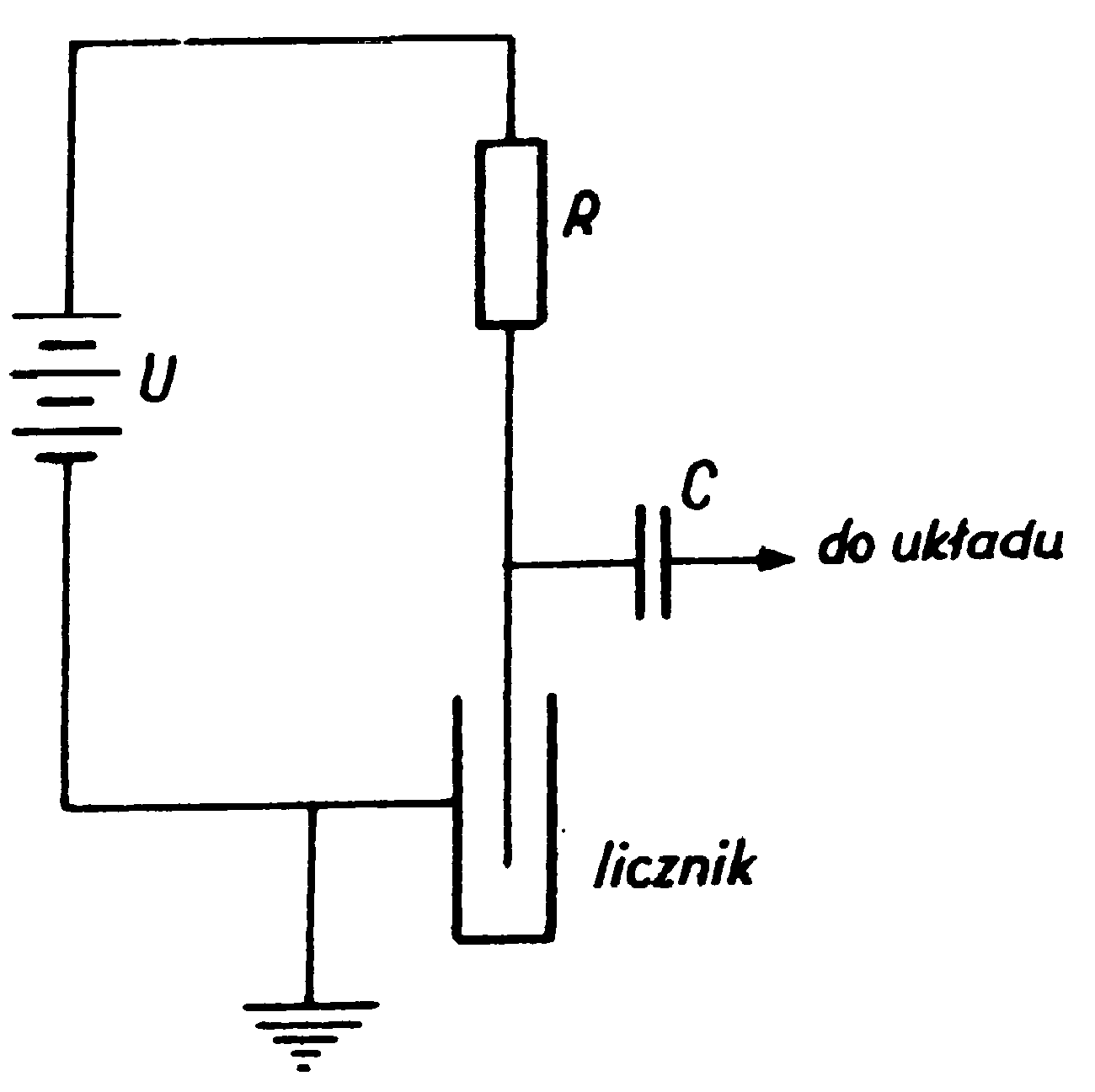
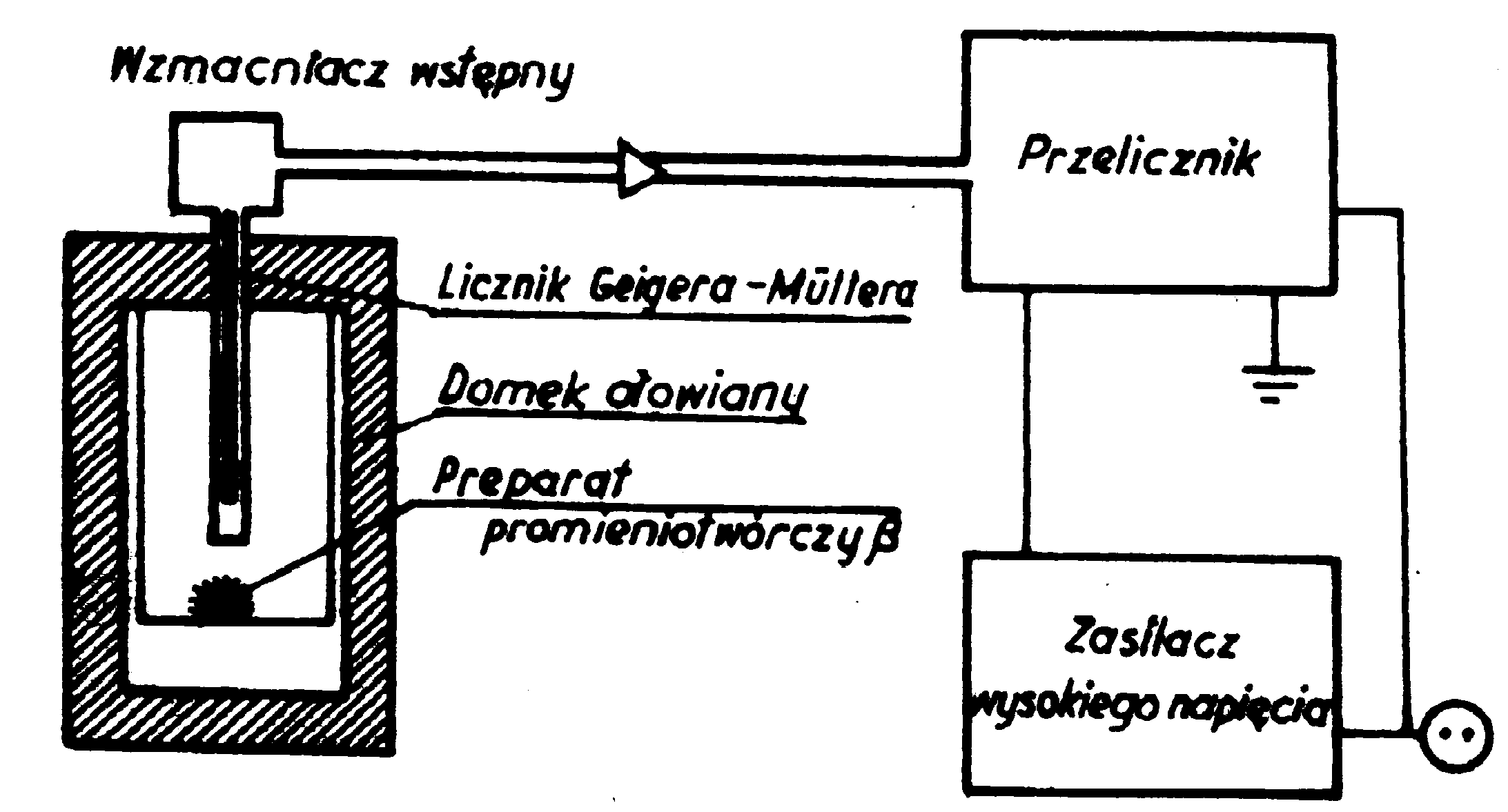
Do elektrod licznika przykłada się stałe napięcie, które wytwarza między nimi pole elektryczne. Cząstka promieniowania wchodząc do wnętrza licznika jonizuje gaz i zapoczątkowuje wyładowanie lawinowe, które przebiega pod wpływem pola elektrycznego licznika. Wyładowanie to jednak nie trwa długo, gdyż licznik dzięki swym właściwościom w małym ułamku sekundy gasi wyładowanie i znowu jest gotowy na przyjęcie następnej cząstki. W czasie tego bardzo krótko trwającego wyładowania płynie przez licznik prąd elektryczny. Prąd ten płynie przez szeregowo z licznikiem połączony opór R dając na nim krótkotrwały spadek napięcia. Otrzymujemy impuls napięciowy. Impulsy takie są przez dalsze urządzenia elektroniczne wzmacniane i liczone (rys. 2).

Przy posługiwaniu się licznikiem Geigera-Mullera bardzo ważna jest znajomość jego charakterystyki. Jest to zależność liczby impulsów rejestrowanych przez licznik w jednostce czasu od napięcia U przyłożonego do licznika. Zależność tę podaje się dla stałej liczby cząstek padających na licznik. Przy napięciu Up zaczynają się pojawiać impulsy w liczniku. Napięcie to nazywa się napięciem progu Geigera. Ze wzrostem napięcia liczba impulsów rejestrowana w jednostce czasu szybko rośnie. Przy napięciu U1 krzywa zagina się i utrzymuje małe nachylenie aż do napięcia U2. Przy wyższych napięciach tworzą się impulsy wielokrotne i dlatego ich liczba w jednostce czasu szybko wzrasta. Część krzywej odpowiadającą przedziałowi napięć od U1 do U2 nazywamy plateau charakterystyki. Długość i nachylenie plateau charakteryzuje dobroć licznika. Im długość jest większa i nachylenie jest mniejsze, tym licznik jest lepszy.

Schemat układu pomiarowego:

Zależność liczby impulsów rejestrowanych przez licznik w jednostce czasu od napięcia przyłożonego do licznika (przy czasie pomiaru t=40s):

U [V]	N [impuls]
450	637
460	767
470	845
480	865
490	797
500	780
510	732
520	733
530	774
540	796
550	816
560	787
570	901
580	920
590	1010
600	993
610	989
620	1100
630	1294
640	1284
650	1340

Zależność liczby impulsów od napięcia przedstawia wykres (odczytujemy z niego wartość napięcia Uw - 1/3 wykresu):

Przyjmujemy napięcie Uw = 500V a pomiary liczby impulsów przy tym napięciu zawiera tabela:

Pomiar tła				Pomiar preparatu
czas [s]	Ntł [imp]	Itł [imp/s]	mtł	czas [s]	N [imp]	I [imp/s]	m	I0=I-Itł
400	184	0,46	0,034	400	7699	19,247	0,219	18,787	0,222
400	154	0,385	0,031	400	7614	19,035	0,218	18,65	0,22
400	176	0,44	0,033	400	7778	19,445	0,22	19,005	0,223

Opracowanie wyników pomiarów:

W przypadku rozpadu radioaktywnego wartość mierzonej wielkości nie jest stała. Liczba cząstek wysyłanych z preparatu promieniotwórczego w różnych odstępach czasu nie jest stała, lecz fluktuuje w pobliżu pewnej wartości średniej według prawa wielkości statystycznych. Dlatego przy pomiarach promieniowania jonizującego należy określić z jak najmniejszym błędem tę średnią wartość. Statystyczną dokładność pomiarów charakteryzuje się średnim błędem kwadratowym m.

Natężenie promieniowania, wyrażające szybkość liczenia impulsów, obliczamy ze wzoru:

gdzie: N- liczba impulsów, t- czas pomiaru N impulsów

Z podobnego wzoru obliczamy natężenie promieniowania pochodzące od tła:

Średni błąd kwadratowy pomiaru natężenia tła i natężenia pochodzącego od preparatu i tła obliczamy na podstawie wzorów:

Otrzymujemy więc:

I₁=( 19,247 ±0,219) imp/s Itł₁=( 0,46 ± 0,034 ) imp/s

I₂=( 19,035 ±0,218) imp/s Itł₂=( 0,385 ± 0,031) imp/s

I₃=( 19,445 ± 0,22 ) imp/s Itł₃=( 0,44 ± 0,033 ) imp/s

Natężenie promieniowania pochodzące od samego preparatu obliczamy ze wzoru:

a błąd samego źródła:

stąd:

Io₁=( 18,787 ± 0,222 ) imp/s

Io₂=( 18,65 ± 0,22 ) imp/s

Io₃=( 19,005 ± 0,223 ) imp/s

Ostatecznie więc, otrzymujemy natężenie promieniowania samego preparatu i jego błąd (obliczając wartości średnie z trzech pomiarów):

Io=( 18,814 ± 0,222 ) imp/s

Rys. 2 Schemat połączeń obwodu licznika Geigera-Mullera

Rys. 1 Schemat licznika Geigera-Mullera (okienkowo-ostrzowego):

1-cylindryczna katoda, 2-anoda, 3-okienko, 4-izolacja

---