Ćwiczenie 56

Badanie wpływu temperatury na przewodnictwo elektryczne

przewodników i półprzewodników

Przyrządy:

Termostat, płytka z badanymi elementami w kąpieli olejowej, cyfrowe mierniki uniwersalne, termometr cyfrowy z sondami temperaturowymi.

Opór elektryczny przewodników w temperaturach dużo wyższych od temperatury Debye'a rośnie liniowo wraz ze wzrostem temperatury:

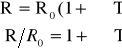
(1)

gdzie: R₀ - opór elektryczny przewodnika w temperaturze otoczenia

ΔT - przyrost temperatury

α - temperaturowy współczynnik oporności elektrycznej

Dla półprzewodników w tym zakresie temperatur opór elektryczny maleje ekspotencjalnie ze wzrostem temperatury:

(2)

gdzie: E - szerokość pasma wzbronionego

k - stała Boltzmana

R_p0 - stała oporności zależna od koncentracji nośników ładunku w stanie podstawowym i

ich ruchliwości

Logarytmując obustronnie równanie (2) otrzymamy liniową zależność lnR od odwrotności temperatury w skali bezwzględnej 1/T [K^-1]:

(3)

Jak wynika ze wzorów (1) i (3) temperaturowy współczynnik oporności α badanego przewodnika, szerokość pasma wzbronionego E i stałą R_po dla badanego półprzewodnika, wyznaczyć można w oparciu o parametry prostych regresji (y= ax +b) dopasowanych do wyznaczonych eksperymentalnie zależności:

1. R/R_o= f(ΔT) - dla przewodnika




2. R = f (1/T) - dla półprzewodnika

Przebieg ćwiczenia

1. Do wyprowadzeń badanych elementów umieszczonych na płycie pomiarowej przyłączyć odpowiednie mierniki oporności a końcówki sond temperaturowych do wejść T₁ i T₂ termometru cyfrowego.

2. Zanurzyć płytę pomiarową z badanymi elementami w kąpieli olejowej, przemieszać olej i po czasie około 2 min odczytać: temperaturę początkową kąpieli olejowej panującą w otoczeniu badanych elementów oraz wartości oporności zmierzoną w układzie pomiarowym: przewodnika (R₁) i półprzewodnika (R₂).

3. Włączyć grzałkę pomocniczą i grzałkę termostatu (moc H3) i odczytywać wartości oporności badanych elementów, co około 5°C, w zakresie od temperatury początkowej do około 80°C kąpieli olejowej (zwykle 12 pomiarów).

4. Wyniki pomiarów zestawić w tab.1 wraz z wynikającymi wprost z tych pomiarów wartościami pozostałych wielkości, tj. przyrosty oporności ΔR₁ = R_1n - R_1n-1 i ΔR₂ = R_2n - R_2n-1 ( n - numer kolejnego pomiaru), wartości ilorazów R₁/R₀₁ (dla przewodnika), wartości temperatury i odwrotności temperatury w skali bezwzględnej (dla półprzewodnika).

5. Obliczyć parametry prostych korelacji na podstawie eksperymentalnych wartości:

y =R₁/R₀₁, x=ΔT - dla przewodnika

y =lnR₂, x=1/T - dla półprzewodnika

i zestawić ich wartości w odpowiednich jednostkach pod tab.1.

6. Obliczyć: szerokość pasma wzbronionego E w elektronowoltach i wartość stałej R_p0. Oszacować błąd bezwzględny ΔE i ΔR_p0.

7. Wypełnić tab.2 wyznaczonymi doświadczalnie wartościami.

8. Sporządzić wykresy:

1. R/R_o = f(ΔT) - dla przewodnika

2. lnR = f(1/T) - dla półprzewodnika

3. R = f(T) - dla półprzewodnika

9. Na wykresach a) i b) wykreślić odpowiednie proste korelacji, a na wykresie c) krzywą
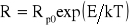
   , dla której wartości R_p0 i E wyznaczono na podstawie wykonanych pomiarów. [W przypadku regresji liniowej należy zaznaczyć dwa punkty, których płożenie określone jest przez wartości parametrów a i b, i przeprowadzić przez nie prostą. W przypadku krzywej c) nanieść punkty teoretyczne i wykreślić przy pomocy krzywika przechodzącą przez nie krzywą].

Tab.1.

t [^oC]	przewodnik				półprzewodnik
		ΔT [K]	R1 [Ω]	ΔR1 [Ω]	R1/Ro	T [°K]	1/T 10^-3[K^-1]	R2 [kΩ]	ΔR2 [kΩ]	lnR2

ΔR₁ = R_1n - R_1n-1 ; ΔR₂ = R_2n - R_2n-1 (n - numer kolejnego pomiaru)

a = [ ] b = [ ] a = [ ] b = [ ]

Δa = [ ] Δb = [ ] Δa = [ ] Δb = [ ]

Tab.2.

przewodnik		półprzewodnik
R/Ro (ΔT=0) ± Δ(R/Ro)	α ± Δα 10^-3[ ]	Rp0 ± ΔRpo [ ]	E/k [ ]	E ± ΔE [ ]

Wymagania:

• Omówić model pasmowy przewodnictwa elektrycznego przewodników oraz półprzewodników samoistnych i domieszkowych.

• Omówić wpływ temperatury na oporność elektryczną ciał stałych i przedstawić wyprowadzenie równania (2).

• Wyjaśnić znaczenie wielkości: temperatura Debye'a, poziom Fermiego, opór resztkowy

• Omówić zjawisko nadprzewodnictwa i podstawowe własności nadprzewodników.

---