7. Metody badania asocjacji i sekwencji

Analiza asocjacji ma na celu identyfikację i opis związków pomiędzy zjawiskami występującymi jednocześnie (czy klienci supermarketu kupujący mleko zaopatrują się również w płatki kukurydziane, czy klienci posiadający ubezpieczenia AC zawierane przez pewnego pośrednika nie zgłaszają znacznie częściej niż inni klienci firmy ubezpieczeniowej faktu kradzieży pojazdu). Badanie sekwencji uwzględnia czynnik czasu i ma na celu określenie związków pomiędzy zjawiskami uszeregowanymi w czasie (czy nabywcy magnetowidów kupują kamery; czy użytkownicy telefonii komórkowej, którzy wykonują niewiele, ale stosunkowo długich rozmów telefonicznych częściej wypowiadają umowę operatowi niż użytkownicy rozmawiający częściej, ale krócej).

1. Analiza zawartości koszyków sklepowych

Metoda analizy zawartości koszyków sklepowych (ang. market-basket analysis) jest chyba najpopularniejszą metodą badania asocjacji. Nazwa metody nawiązuje do jej pierwotnego przeznaczenia badania, które towary kupowane są przez klientów łącznie. Taka informacja może być przydatna przy planowaniu sposobu rozlokowania towarów w sklepie, przy projektowaniu akcji promocyjnych, czy też przy planowaniu zaopatrzenia. Współczesne zastosowania metody są znacznie szersze i obejmują wszystkie te dziedziny, w których istotne jest badanie współwystępowania pewnych zjawisk.

Aparat matematyczny służący opisowi łącznego występowania pewnych zjawisk jest bardzo prosty i obejmuje zwykle metody szacowania prawdopodobieństwa zajścia pewnych zjawisk na podstawie informacji zgromadzonych w bazie danych. Poszukiwanie rzeczywiście istniejących zależności odbywa się zwykle metodą prób i błędów - rozpatrywane są wszelkie możliwe związki, dla nich wszystkich szacowane są prawdopodobieństwa ich wystąpienia i wybierane są te, które znajdują potwierdzenie w danych. Taki sposób postępowania powoduje, że liczba powtórzeń realizacji prostej procedury obliczeniowej bardzo szybko rośnie i powoduje, że czas niezbędnych obliczeń może przekroczyć wartość akceptowalną przez użytkownika.

W celu zaprezentowania idei analizy zawartości koszyków sklepowych posłużymy się prostym przykładem nawiązującym do pierwotnego obszaru zastosowań metody. Niech obiektem naszych zainteresowań będzie supermarket oferujący swoim klientom n różnych towarów: X₁, X₂, …, X_n. Celem badań będą reguły, którymi kierują się klienci kupując łącznie pewną grupę towarów. W trakcie badań będziemy chcieli zidentyfikować te prawidłowości i je zweryfikować na podstawie danych dotyczących realizowanych w sklepie transakcji. Niech K oznacza łączną liczbę transakcji zrealizowanych w sklepie w badanym okresie (każda z transakcji polega na zakupie jednego lub kilku towarów - liczba transakcji jest równa liczbie paragonów kasowych). Prawidłowości badane za pomocą przedstawianej metody analizy mają postać:

jeżeli A to B

gdzie A oraz B są zdarzeniami polegającymi na zakupie jednego towaru bądź pewnej ich grupy. Przykładowa reguła może mieć postać

jeżeli (X₂ i X₇₇ i X₁₂₃) to X₁₂

jej interpretacja jest następująca: klienci kupujący towary X₂, X₇₇ oraz X₁₂₃ kupują również towar oznaczony symbolem X₁₂.

Punktem wyjścia do przeprowadzanych analiz jest określenie liczby transakcji zawierających każdy z towarów. Niech K(X_i) oznacza liczbę transakcji, w trakcie których kupiono (wyłącznie bądź też między innymi) towar X_i. Dzieląc wyznaczone wartości przez K oszacować można prawdopodobieństwo tego, że wśród zakupionych towarów znajdzie się interesujący nas towar. Na przykład obliczone tą metodą prawdopodobieństwo zakupu towaru X_i wynosi:

. (1)

Na podobnej zasadzie obliczyć można liczbę transakcji, w trakcie których zakupiony został pewien zbiór towarów. Analizując fakt łącznego zakupu dwóch towarów wyznaczyć można wartości K(X_i, X_j) będące liczbą transakcji obejmujących jednocześnie towary X_i oraz X_j. W podobny sposób można zliczać liczbę transakcji obejmujących określony trójki towarów, bądź też ich zbiory o jeszcze większej liczebności. Wyznaczone liczebności mogą służyć do szacowania prawdopodobieństw, na przykład:

(2)

jest oszacowanym na podstawie danych prawdopodobieństwem zdarzenia polegającego na tym, że w trakcie dokonywania zakupów klient jednocześnie kupi towary X_i oraz X_j. Przeprowadzając powyższe obliczenia można określić, które zestawienia towarów występują najczęściej w koszykach klientów supermarketu.

Wspomniane powyżej reguły dokonywania zakupów mają postać „jeżeli A to B” i do ich opisu posłuży pojęcie prawdopodobieństwa warunkowego p(B|A), które mówi nam, jakie jest prawdopodobieństwo zajścia zdarzenia B pod warunkiem, że wystąpiło zdarzenie A. Do oszacowanie tego typu prawdopodobieństw wykorzystywać będziemy częstości względne:

, (3)

na przykład:

.

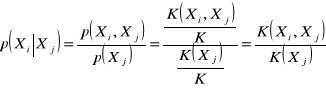
wyznaczoną wartość
można zinterpretować jako prawdopodobieństwo zakupu towaru X_i przez klienta, który kupił towar X_j. Wyrażona w ten sposób wartość określa poziom zaufania do reguły: jeżeli X_j to X_i. Im wyższym poziomem zaufania charakteryzuje się dana reguła, tym mocniej potwierdzają ją zgromadzone dane.

Wyznaczone dla poszczególnych reguł poziomy zaufania są miarami o charakterze względnym - pozwalają określić, która z dwóch reguł jest lepsza, ale nie pozwalają na stwierdzenie, czy nawet ta lepsza jest naprawdę przydatna i czy warto ją stosować. O rzeczywistej wartości reguły świadczyć może porównanie wartości
oraz
. Daną regułę można uznać za przydatną, gdy poziom zaufania do niej wyrażony przez prawdopodobieństwo warunkowe
jest większe od prawdopodobieństwa
- inaczej mówiąc, że prawdopodobieństwo tego, że klient, który kupił towar X_j kupi również towar X_i jest większe od prawdopodobieństwa zakupu towaru X_i.

Uogólniając przedstawione powyżej rozumowanie dotyczące dwóch towarów sformułować można miarę jakości reguły decyzyjnej jeżeli A to B w postaci wskaźnika δ:

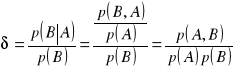
. (4)

Tylko reguły charakteryzujące się wskaźnikiem δ większym od jedności stanowią wartościową informację o zasadach postępowania klientów.

Oprócz reguł typu jeżeli A to B często przydatne mogą być również formuły o postaci jeżeli A to nieprawda, że B. Sposób oceny reguł tego typu jest analogiczny jak formuł scharakteryzowanych powyżej.

Uwzględniony w ramach analizy zbiór rozpatrywanych towarów obejmujący X₁, X₂, …, X_n jest często rozszerzany o zbiór towarów wirtualnych V₁, V₂, …, V_m. Można wskazać na dwie podstawowe przesłanki wprowadzenia towarów wirtualnych:

1. asortyment rzeczywistych towarów dostępnych dla klientów supermarketu (czyli X₁, X₂, …, X_n) jest często bardzo szeroki, co powoduje możliwość wygenerowania olbrzymiej liczby potencjalnych reguł postępowania klientów, których sprawdzenie wymaga bardzo dużych, praktycznie niemożliwych do zaakceptowania, nakładów czasowych. W celu zmniejszenia liczebności pierwotnego zbioru towarów zastępuje się je towarami wirtualnymi reprezentującymi nie pojedyncze produkty, ale ich grupy (np. pieczywo, sery topione, owoce, proszki do prania). Rozpatrywanie grup towarów zamiast pojedynczych produktów jest wskazane z dwóch powodów: zmniejsza liczbę rozpatrywanych przypadków oraz likwiduje (często niepotrzebne z praktycznego punktu widzenia) uszczegółowienie asortymentu (np. oddzielne rozpatrywanie każdego rodzaju proszku do prania lub też każdego gatunku papierosów);

2. wprowadzone do analizy towary wirtualne mogą reprezentować inne informacje przydatne w czasie analizy (np. dzień tygodnia, godzinę zakupu, sposób dokonania płatności /gotówka, karta płatnicza, bon towarowy/, ogólną wielkość dokonanej transakcji). Uwzględnienie tego typu informacji w trakcie analizy może znacząco wzbogacić wiedzę o sposobie postępowania klientów.

Jak już wskazano we wcześniejszej części tekstu zaprezentowana metoda analizy zawartości koszyków sklepowych posiada potencjalnie nieograniczony obszar zastosowań. Może być przydatna we wszystkich tych przypadkach, w których badaniu podlega współwystępowanie pewnych zjawisk.

1. Badanie sekwencji

W przedstawionej powyżej metodzie analizy przyjęto założenie, że badanie dotyczy zjawisk występujących jednocześnie - nie uwzględnialiśmy zatem upływającego czasu. Aspekt czasu odgrywa natomiast zasadniczą rolę przy badaniu sekwencji, czyli prawidłowości związanych z uporządkowaniem pewnych zjawisk w czasie. W badaniach sekwencji uwaga skupiona jest na prawidłowościach związanych z kolejnością, w jakiej zachodzą pewne zjawiska, natomiast mniejsze znaczenie odgrywają informacje pozwalające na dokładną lokalizację w czasie rozpatrywanych zjawisk.

Eksploracja danych mająca na celu identyfikację i opis występujących sekwencji może mieć bardzo znaczenie przy próbach rozwiązania problemów o charakterze ekonomicznym. Chcąc wskazać na przykładowe dziedziny jej zastosowań można wymienić:

• identyfikację i analizę prawidłowości związanych z zachowaniem się klientów dokonujących zakupów (np. klient, który kupił komputer po pewnym czasie decyduje się na zakup drukarki); wykrycie tego typu reguł umożliwia prognozowanie i ułatwia planowanie działalności handlowej;

• rozpoznanie sposobów postępowania i prognozowanie zachowań klientów korzystających z różnego rodzaju usług (bankowych, telekomunikacyjnych) - tego typu badania mogą być pomocne przy wykrywaniu klientów stwarzających zagrożenie dla usługodawcy (np. klientów chcących zrezygnować z oferty usługodawcy);

• wykrywanie nadużyć;

• analizę sposobu korzystania z serwisów internetowych - np. w celu ich właściwego zaprojektowania.

Stosowane metody badawcze wykorzystywane przy badaniu sekwencji są bardzo zbliżone do narzędzi pozwalających na opisane wyżej badanie asocjacji. Przy czym należy pamiętać, że najpoważniejszym problemem, pojawiającym się przy badaniu sekwencji jest problem wstępnej identyfikacji potencjalnie powiązanych ze sobą zjawisk. W przypadku badań marketingowych problem te sprowadza się do identyfikacji klientów, gdyż powinniśmy analizować zależności pomiędzy operacjami realizowanymi przez tego samego klienta. W sytuacji, gdy klient pozostaje anonimowy (np. klient kupujący w supermarkecie) analiza sekwencji zdarzeń jest bardzo utrudniona, albo wręcz niemożliwa. Bardzo popularnym narzędziem pozwalającym na identyfikację klientów są różnego rodzaju karty klienta, które kupującemu zapewniają różnego rodzaju udogodnienia (np. rabaty), zaś sprzedającemu pozwalają na identyfikację kupujących określone towary lub usługi.

150

---