Wydział Górniczy		Swędrowska Dominika			Budownictwo III
Nr ćw.: 10	TEMAT: Oznaczenie kąta tarcia i spójności skał w próbie trójosiowego ściskania.
Grupa 2/2			Rok akademicki 2002/2003	Data wykonania 09.10.2002		OCENA:

Cel ćwiczenia:

Oznaczenie za pomocą aparatu do trójosiowego ściskania kąta tarcia wewnętrznego i spójności skały.

Opracowanie wyników:

Rodzaj skał						less
Wartość naprężeń głównych σ1 i σ2 dla próbki nr						1
Czas pomiaru min	Zmiana wysokości próbki 10^-2 mm	Wskazanie dynam. Δx 10^-2 mm	Stała dynam. k N/10^-2 mm	Siła pionowa F N	Powierzchnia próbki S m^2	Napręż. pionowe σ1 MPa	Napręż. poziome σ3 MPa
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 5,5 6,0 6,5 7,0 7,2	6 22 33 37 39 37 38 38 38 35 37 35 35 32 13	6 28 61 98 137 174 212 250 288 323 360 395 430 462 475	8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305	49,83 232,54 506,61 813,89 1137,79 1445,07 1760,66 2076,25 2391,84 2682,52 2989,80 3280,48 3571,15 3836,91 3944,88	0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335	0,04 0,21 0,45 0,72 1,00 1,27 1,55 1,83 2,11 2,37 2,64 2,89 3,15 3,39 3,48	0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1

Rodzaj skał						less
Wartość naprężeń głównych σ1 i σ2 dla próbki nr						2
Czas pomiaru min	Zmiana wysokości próbki 10^-2 mm	Wskazanie dynam. Δx 10^-2 mm	Stała dynam. k N/10^-2 mm	Siła pionowa F N	Powierzchnia próbki S m^2	Napręż. pionowe σ1 MPa	Napręż. poziome σ3 MPa
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 5,5 6,0 6,5 7,0 7,5 8,0 8,3	3 18 28 36 36 36 36 38 37 36 39 34 37 36 30 31 12	3 21 49 85 121 157 193 231 268 304 343 377 414 450 480 511 523	8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305	24,92 174,41 406,95 705,93 1004,91 1303,89 1602,87 1918,46 2225,74 2524,72 2848,62 3130,99 3438,27 3737,25 3986,40 4243,86 4343,52	0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335	0,02 0,15 0,36 0,62 0,89 1,15 1,41 1,69 1,96 2,23 2,51 2,76 3,03 3,30 3,52 3,74 3,83	0,2 0,2 0,2 0,2 0,2 0,2 0,2 0,2 0,2 0,2 0,2 0,2 0,2 0,2 0,2 0,2 0,2

Rodzaj skał						less
Wartość naprężeń głównych σ1 i σ2 dla próbki nr						3
Czas pomiaru min	Zmiana wysokości próbki 10^-2 mm	Wskazanie dynam. Δx 10^-2 mm	Stała dynam. k N/10^-2 mm	Siła pionowa F N	Powierzchnia próbki S m^2	Napręż. pionowe σ1 MPa	Napręż. poziome σ3 MPa
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 5,5 6,0 6,5 7,0 7,5 8,0 8,5 8,7	4 24 30 29 27 32 33 34 34 35 35 36 35 35 35 29 30 13	4 28 58 87 114 146 179 213 247 282 317 353 388 423 458 487 517 530	8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305	33,22 232,54 481,69 722,54 946,77 1212,53 1486,60 1768,97 2051,34 2342,01 2632,69 2931,67 3222,34 3513,02 3803,69 4044,54 4293,69 4401,65	0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335	0,03 0,21 0,42 0,64 0,84 1,07 1,31 1,56 1,81 2,07 2,32 2,59 2,84 3,10 3,36 3,57 3,79 3,88	0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3 0,3

Rodzaj skał						less
Wartość naprężeń głównych σ1 i σ2 dla próbki nr						4
Czas pomiaru min	Zmiana wysokości próbki 10^-2 mm	Wskazanie dynam. Δx 10^-2 mm	Stała dynam. k N/10^-2 mm	Siła pionowa F N	Powierzchnia próbki S m^2	Napręż. pionowe σ1 MPa	Napręż. poziome σ3 MPa
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 5,5 6,0 6,5 7,0 7,5 8,0 8,5 9,0 9,5 10,0 10,5 10,6	5 12 23 27 27 29 29 27 31 35 36 31 41 36 36 36 35 35 30 30 22 2	5 17 40 67 94 123 152 179 210 245 281 312 353 389 425 461 496 531 561 591 613 615	8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305 8,305	41,53 141,19 332,20 556,44 780,67 1021,52 1262,36 1486,60 1744,05 2034,73 2333,71 2591,16 2931,67 3230,65 3529,63 3828,61 4119,28 4409,96 4659,11 4908,26 5090,97 5107,58	0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335 0,0011335	0,04 0,12 0,29 0,49 0,69 0,90 1,11 1,31 1,54 1,80 2,06 2,29 2,59 2,85 3,11 3,38 3,63 3,89 4,11 4,33 4,49 4,51	0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4 0,4

Wyznaczanie kąta tarcia wewnętrznego i spójności metodą analityczną:

Ze względu na niejednorodność badanej skały oraz brak identyczności próbek, wartości φ i c należy określić analitycznie.

Dla każdej pary naprężeń ścinających (σ₁ i σ₃) obliczamy:

oraz

gdzie:

p_i - odcięta punktu maksymalnych naprężeń stycznych (współrzędna środka koła Mohra), Pa

q_i - rzędna punktu maksymalnych naprężeń stycznych (promień koła Mohra), Pa

i - numer próbki

Na wykresie q = f(p) uzyskujemy 4 punkty dla których znajdujemy równanie prostej:

q = ptgδ + b

gdzie:

δ - kąt nachylenia prostej,

b - odcinek rzędnej od początku układu do przecięcia z prostą, Pa,

pozostałe symbole jak poprzednio

Obliczenia δ i b należy przeprowadzić sposobem analitycznym, stosując zasadę aproksymacji liniowej metodą najmniejszych kwadratów:

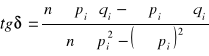
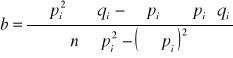
gdzie:

n - liczba uwzględnianych punktów na wykresie q = f(p),

p_i - odcięta punktu maksymalnych naprężeń, Pa,

q_i - rzędna punktu maksymalnych naprężeń, Pa.

Uzyskane wartości δ i b pozwalają określić szukane parametry kąta tarcia wewnętrznego φ i spójności c z następujących prostych zależności:

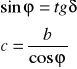
Maksymalne wartości naprężeń stycznych w układzie osi współrzędnych p - q.
Nr próbki i		σ1 MPa	σ3 MPa	pi MPa	qi MPa		pi^2	pi • qi
1 2 3 4		3,48 3,83 3,88 4,51	0,1 0,2 0,3 0,4	1,79 2,02 2,09 2,45	1,69 1,82 1,79 2,05		3,20 4,08 4,37 6,00	3,03 3,68 3,74 5,02
Σ				Σpi=8,35	Σqi=7,35		Σpi^2=17,66	Σpiqi=15,47
								(Σpi) ^2=69,73
tg δ -	tanges kąta nachylenia prostej p - q,					0,5456
b -	odcinek rzędnej odcięty przez prostą p - q					0,69
φ -	uśredniony kąt tarcia wewnętrznego dla danego rodzaju skały					33,05
c -	uśredniona spójność dla danego rodzaju skały, MPa					0,84

Wnioski:

Badanie obejmowało cztery próbki lessu. Wyznaczono graficznie i analitycznie spójność i kąt tarcia wewnętrznego. W przypadku graficznym jednak nie można jednoznacznie określić obwiedni kół Mohra, gdyż koła te różnią się od siebie bardzo wielkością. Przyjąć można, że w przypadku graficznym spójność c równa się

8,6•10⁵ Pa a kąt φ=31°.

Porównując wyniki analityczne z graficznymi mamy:

31°<φ<33,5°

0,84<c<0,86 [Mpa]

Są to wartości zbliżone do siebie, więc można uznać poprawność wykonania ćwiczenia. Spoistość c jest związana z siłą kohezji czyli przyczepnością międzycząsteczkową. Less jak widać nie posiada dużej spoistości, gdyż nie jest skałą zwięzłą, dla których „c” osiąga znacznie większe wartości.

---