PRACOWNIA ZAKŁADU FIZYKI TECHNICZNEJ POLITECHNIKI LUBELSKIEJ |
|||||
Nazwisko i imię Adamek Tomasz studenta |
Instytut i symbol grupy ED 3.1 |
||||
Data wykonania ćw 29-10-98 |
Symbol ćwiczenia 4.2 |
Temat: Wyznaczanie współczynnika osłabienia oraz energii maksymalnej promieniowania β |
|||
Zaliczenie: |
Ocena: |
Data: |
Podpis: |
||
1.Tabele pomiarów i obliczenia:
Pomiar tła
Lp. |
Ntł |
Ntł |
LnNtł |
t |
-- |
-- |
-- |
-- |
s |
1 |
149 |
|
|
|
2 |
156 |
145.75 |
4.98 |
200 |
3 |
140 |
|
|
|
4 |
138 |
|
|
|
Pomiary dla Ss-90(131)
Lp. |
xi |
t |
R0 |
RAli |
Ri |
Ni |
yi=LnNi |
-- |
cm |
s |
g/cm2 |
g/cm2 |
g/cm2 |
-- |
-- |
1 |
0 |
|
|
0 |
0.00487 |
3035 |
8.01 |
2 |
0.02 |
|
|
0.054 |
0.05887 |
2048 |
7.62 |
3 |
0.04 |
|
|
0.108 |
0.11288 |
1485 |
7.3 |
4 |
0.06 |
200 |
0.00487 |
0.162 |
0.16687 |
1106 |
7 |
5 |
0.08 |
|
|
0.216 |
0.22087 |
752 |
6.62 |
6 |
0.1 |
|
|
0.27 |
0.27487 |
537 |
6.28 |
7 |
0.12 |
|
|
0.324 |
0.32887 |
383 |
5.94 |
8 |
0.14 |
|
|
0.378 |
0.38287 |
313 |
5.74 |
|
|
|
|
|
|
|
|
Rfs=10-3g/cm2 hpow=3cm ρpow=1.29 10-3g/cm3 ρAl.=2.7g/cm2
Rpow=hpowρpow=3cm 1.29 10-3g/cm3=3.87 10-3g/cm2
R0=Rpow+Rfs=3.87 10-3g/cm2+ 1 10-3g/cm2=4.87 10-3g/cm2
xi=0.02
Ral=ρAlxi=2.7g/cm30.02=0.054g/cm2
Ni=2048
yi=LnNi=7.62
Ri=R0+Rali=4.87 10-3g/cm2+54 10-3g/cm2=58.87 10-3g/cm2
2.Cel ćwiczenia.
Celem ćwiczenia jest wyznaczenie aktywności preparatu promieniotwórczego β na podstawie zmierzonych częstości zliczeń impulsów, energii maksymalnej promieniowania β użytego izotopu, maksymalnego zasięgu Rmax cząsteczek β oraz współczynników: liniowego i masowego.
3.Obliczenia.
Aby wyznaczyć μ oraz N0 zastosujemy metodę najmniejszych kwadratów, sprawdzając równanie N=N0e-μx do postaci liniowej. Logarytmując stronami otrzymamy: LnN=LnNo-μx. Jeśli wprowadzimy oznaczenia: y=LnN, a=-μ, b=LnN0, to otrzymamy równanie prostej y=ax+b.
Lp. |
xi |
Ni |
yi=LnN |
xi2 |
xiyi |
Wi |
μ=-a |
b=LnN0 |
N0 |
||
-- |
cm |
-- |
-- |
cm2 |
cm |
-- |
1/cm |
-- |
-- |
||
1 |
0 |
3035 |
8.01 |
0 |
0 |
1 |
|
|
|
||
2 |
0.02 |
2048 |
7.62 |
0.0004 |
0.1524 |
1 |
|
|
|
||
3 |
0.04 |
1485 |
7.3 |
0.0016 |
0.292 |
1 |
|
|
|
||
4 |
0.06 |
1106 |
7 |
0.0036 |
0.42 |
1 |
16.6 |
7.9758 |
2909.77 |
||
5 |
0.08 |
752 |
6.62 |
0.0064 |
0.528 |
1 |
|
|
|
||
6 |
0.1 |
537 |
6.28 |
0.01 |
0.628 |
1 |
|
|
|
||
7 |
0.12 |
383 |
5.94 |
0.0144 |
0.7128 |
1 |
|
|
|
||
8 |
0.14 |
313 |
5.74 |
0.0196 |
0.8036 |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
D=
=8 0.056-0.562=0.1344cm2
a===
b===
LnN=LnN0-μx ⇒y=-ax+b, y=LnN, a=-μ, b=LnN0⇒N0=eb
Wartość liniowego współczynnika osłabienia wynosi:
μ=-a=16.6cm-1
N0=e7.97583=2909.77
Lp. |
xi |
b |
a |
yi' |
yi |
|
|
|
|
-- |
cm |
-- |
cm-1 |
-- |
-- |
-- |
-- |
cm-1 |
-- |
1 |
0 |
|
|
7.97583 |
8.01 |
0.03417 |
0.0011 |
|
|
2 |
0.02 |
|
|
7.6438 |
7.62 |
0.02383 |
0.0005 |
|
|
3 |
0.04 |
|
|
7.3118 |
7.3 |
0.01183 |
0.0001 |
|
|
4 |
0.06 |
7.9758 |
-16.6 |
6.9798 |
7 |
0.02017 |
0.0004 |
0.3726 |
0.0311 |
5 |
0.08 |
|
|
6.6478 |
6.62 |
0.02783 |
0.0007 |
|
|
6 |
0.1 |
|
|
6.3158 |
6.28 |
0.03583 |
0.0012 |
|
|
7 |
0.12 |
|
|
5.9838 |
5.94 |
0.04383 |
0.0019 |
|
|
8 |
0.14 |
|
|
5.6518 |
5.74 |
0.08817 |
0.0077 |
|
|
|
|
|
|
|
|
|
|
|
|
Obliczenia dla Lp.=1:
yi'=axi+b
yi'=-16.6 0.02+7.97583=7.64383
=yi'-yi=7.64383-7.62=0.02383
Aby oszacować błąd przy wyznaczaniu μ oraz N0 należy obliczyć błędy wielkości a i b.
===0.3726
===0.0311
natomiast LnN0=b, N0=e0.0311=1.0315
Równanie prostej zapiszemy w postaci:
y=(a+/-a)x+(b+/-b)
w tym przypadku:
LnN=LnN0-μx zatem LnN=(7.97583+/-0.0311)+(-16.6+/-0.3726)x
Współczynnik osłabienia promieniowania β przez aluminium wynosi:
μ=+/-a
μ=(16.6+/-0.3726)cm-1
16.2274cm-1<μ<16.9726cm-1
Błąd względny wyznaczenia współczynnika osłabienia będzie mieć wartość:
δμ==0.022 i procentowo δμ%=2.2%
Liczba zliczeń N0 wyniesie więc:
N0=2909.77+/-1.0315⇒2908.7385<N0<2910.0315
Błąd względny wyznaczenia N0 będzie następujący:
δNo= =0.0003 tzn. δNo%=0.03%
Masowy współczynnik osłabienia otrzymamy dzieląc liniowy współczynnik osłabienia przez gęstość absorbentu:
μm.=μ/ρAl.=6.14cm2/g
Wyznaczanie Rmax:
Z wykresu funkcji: LnN=LnN0-μx odczytujemy xmaxalbo obliczamy na podstawie równania prostej wiedząc, że LnNtł=4.98
LnNtł=axmax+b ⇒ xmax==0.1804cm
Teraz możemy obliczyć zasięg Rmax cząsteczek β
Rmax=R0+ρAlxmax=0.00487+2.7 0.1804=0.49195g/cm2
Wykres funkcji LnN=LnN0-μx
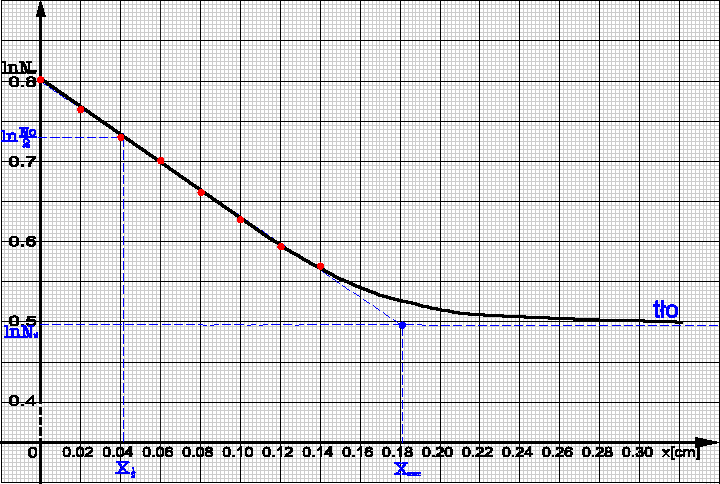
Energia maksymalna promieniowania β użytego izotopu wynosi:
Rmax>0.4g/cm2
Emax=1.75 Rmax+0.281=1.1419MeV
Analiza korelacyjna.
Lp. |
xi |
x |
rxi=xi-x |
yi |
y |
ryi=yi-y |
rxi2 |
ryi2 |
rxiryi |
-- |
cm |
cm |
cm |
-- |
-- |
-- |
cm2 |
-- |
cm |
1 |
0 |
|
-0.07 |
8.01 |
|
1.2 |
0.0049 |
1.44 |
-0.084 |
2 |
0.02 |
|
-0.05 |
7.62 |
|
0.81 |
0.0025 |
0.6561 |
-0.0405 |
3 |
0.04 |
|
-0.03 |
7.3 |
|
0.49 |
0.0009 |
0.2401 |
-0.0147 |
4 |
0.06 |
0.07 |
-0.01 |
7 |
6.81 |
0.19 |
0.0001 |
0.0361 |
-0.0019 |
5 |
0.08 |
|
0.01 |
6.62 |
|
-0.19 |
0.0001 |
0.0361 |
-0.0019 |
6 |
0.1 |
|
0.03 |
6.28 |
|
-0.53 |
0.0009 |
0.2809 |
-0.0159 |
7 |
0.12 |
|
0.05 |
5.94 |
|
-0.87 |
0.0025 |
0.7569 |
-0.0435 |
8 |
0.14 |
|
0.07 |
5.74 |
|
-1.07 |
0.0049 |
1.1449 |
-0.0749 |
|
|
|
|
|
|
|
|
|
|
σx==0 ⇒ rxy==0
Ponieważ współczynnik korelacji (rxy=0) jest równy zero nie ma związku statycznego między badanymi wielkościami lub zjawiskami i odwrotnie.
Drugi sposób wyznaczania współczynnika liniowego i masowego.
Współczynnik μ można również wyznaczyć wprost z zależności N=N0e-μx
biorąc pod uwagę, że grubość warstwy absorbentu powodująca zmniejszenie natężenia wiązki o połowę (tzw. Grubość połówkowego osłabienia x1/2) wynosi:
x1/2= a więc 1454.885, ⇒ =7.282
dla tej wartości odczytujemy z wykresu x1/2lub obliczamy z równania prostej
=ax1/2+b ⇒ x1/2==0.04
a więc współczynnik liniowy wynosi:
μ==17.32cm-1
Natomiast współczynnik masowy wynosi:
μm.==6.41cm2/g
Błąd względny maksymalny pomiaru wielkości μ liczonej ze wzoru μ= ,
gdzie wielkością zmienną jest x1/2. Za błąd bezwzględny maksymalny x1/2
przyjmujemy wartość najmniejszej działki na osi x z wykresu: LnN=LnN0-μx
x1/2=0.002cm
δm.(μ)===0.05 procentowo δm.(μ)%=5%
Błąd bezwzględny maksymalny wynosi:
μm.=δm.(μ) μ=0.05 17.32=0.866cm-1
4.Wynik:
μ=(μ+/-μm.)=(17.32+/-0.866)cm-1 16.454cm-1<μ<18.186cm-1
5.Wnioski:
Wartości współczynnika masowego wyznaczone zarówno jedną jak i drugą metodą są prawie identyczne(μm.=6.41, μm.=6.14).Wartości współczynnika liniowego wyznaczone pierwszą metodą są dokładniejsze gdyż
μm.(1)< μm.(2).Błąd względny maksymalny pomiaru wielkości μ jest mniejszy przy metodzie pierwszej i wynosiδμ%=2.2%.
Wyszukiwarka
Podobne podstrony:
Wyznaczanie współczynnika osłabienia oraz energii maksymal(2), Pracownia Zak˙adu Fizyki Technicznej
Wyznaczanie współczynnika lepkości cieczy metodą Os, Pracownia Zak˙adu Fizyki Technicznej Politech
Wyznaczanie napięcia zapłonu i gaśnięcia lamp y jarzeniowej, Pracownia Zak˙adu Fizyki Technicznej P
Wyznaczanie długości fal świetlnych przepuszczanych przez (2), Pracownia Zak˙adu Fizyki Technicznej
Wyznaczanie współczynników osłabiania promieniowania gamma 1, Pracownia Zak˙adu Fizyki Technicznej P
Wyznaczanie współczynników osłabienia promieniowania g, Pracownia Zak˙adu Fizyki Technicznej Polite
Wyznacznie współczynnika osłabiania promieniowania gamma, Pracownia Zak˙adu Fizyki Technicznej Polit
Wyznaczanie współczynników osłabienia promieniowania, Pracownia Zak˙adu Fizyki Technicznej Politechn
Wyznaczanie współczynnika napięcia powierzchniowego cieczy m, Pracownia Zak˙adu Fizyki Technicznej
Wyznaczanie wspó czynnika lepko ci cieczy metod Ostwalda, Pracownia Zak˙adu Fizyki Technicznej Polit
Wyznaczanie elementów LC metodą rezonansu, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelsk
Wyznaczanie ogniskowych soczewek na podstawie pomiarów odl(2), Pracownia Zak˙adu Fizyki Technicznej
Wyznaczanie stałej Verdeta, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
Wyznaczanie elementów LC obwodu metodą rezonansu - DUDA, Pracownia Zak˙adu Fizyki Technicznej Polite
WYZNACZANIE R WNOWA NIK W E4, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
Wyznaczanie przyspieszenia ziemskiego wahadłem matematycznym, Pracownia Zak˙adu Fizyki Technicznej
więcej podobnych podstron