Pytania na egzamin z fizyki I semestr Budownictwo

1. Międzynarodowy układ jednostek miar SI.

2. Podaj i scharakteryzuj wielkość fizyczną opisaną, iloczynem skalarnym i wektorowym.

3. Wyjaśnij różnicę pomiędzy przemieszczeniem i drogą oraz wyznacz przemieszczenie i drogę dla ruchu opisanego wektorem
   .

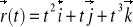
4. Zbadaj ruch ciała opisany przykładowym wektorem
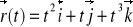
   , (prędkość, przyspieszenie, położenie)

5. Wyznacz położenie, prędkość, przyspieszenie oraz graficznie przyspieszenie styczne i dośrodkowe w dowolnej chwili czasu w rzucie poziomym i ukośnym,

6. Określ równania ruchu w rzucie poziomym i ukośnym i na ich podstawie wyznacz równania toru.

7. Zasady dynamiki Newtona oraz definicja i przykłady układów inercjalnych i nieinercjalnych.

8. Podaj definicję środka masy i wyznacz wektor środka masy dla układu punktów na płaszczyźnie.

9. Udowodnij, że środek masy jednakowych ciał umieszczonych w narożnikach dowolnego trójkąta wypada w punkcie przecięcia środkowych.

10. Wyznacz przyspieszenie dowolnego układu ciał połączonych linkami, zaznacz wszystkie wektory sił, uwzględnij masę bloczków.

11. Opisz siły tarcia, siłę dośrodkową i siłę Coriolisa.

12. Siła Coriolisa. Opisz ruch ciała, które zostało upuszczone z wysokości 100m nad powierzchnią ziemi, na szerokości geograficznej północnej 60⁰ z punktu widzenia obserwatora znajdującego się na powierzchni ziemi.

13. Scharakteryzuj siły bezwładności.

14. Zbadaj całkowitą drogę przebytą przez ciało, poruszające się z przyspieszeniem a = - kv z prędkością początkową v₀.

15. Podaj definicję energii potencjalnej i kinetycznej w polu sił grawitacyjnych i sprężystych.

16. Zasada zachowania pędu - przykład zastosowania w napędzie odrzutowym. Rakieta porusza się w przestrzeni kosmicznej z prędkością V₀. Masa Rakiety wraz z paliwem wynosi M. W celu zmiany prędkości rakieta wyrzuca paliwo o masie m ze stałą prędkością (dm/dt = const). Wyznacz prędkość końcową rakiety.

17. Zderzenie sprężyste - wyprowadzenie wzorów na prędkości ciał po zderzeniu, analiza przypadków omawianych na wykładzie.

18. Moment siły, przyspieszenie kątowe i prędkość kątowa.

19. Równania ruchu obrotowego jako konsekwencja II zasady dynamiki Newtona.

20. Moment pędu oraz prawo zachowania momentu pędu..

21. Moment bezwładności, Twierdzenie Steinera, wyprowadź wzory ma momenty bezwładności walca, rury, kuli, pręta, stożka.

22. Wykaż, że moment bezwładności układu składającego się z dwóch mas m₁ i m₂ odległych o r od siebie względem osi prostopadłej do odcinka łączącego m₁ i m₂ i przechodzącej przez środek masy układu wynosi μr², μ jest masą zredukowaną układu
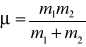
    . Oblicz moment bezwładności molekuły CO względem osi prostopadłej do wiązania przechodzącej przez środek masy molekuły. Długość wiązania C-O wynosi 1,13*10^-10 m.

23. Wyjaśnij doświadczenia prezentowane na wykładzie: koło krzesło, walec pusty i pełny na równi, szpulka babuni, koło sznurek-precesja.

24. Maszyny proste.

25. Drgania harmoniczne.- równanie i rozwiązanie.

26. Położenie, prędkość i przyspieszenie w ruchu harmonicznym.

27. Energia w ruchu harmonicznym.

28. Zasada zachowania energii mechanicznej w ruchu drgającym i w polu grawitacyjnym.

29. Równanie ruchu harmonicznego tłumionego i rozwiązanie.

30. Logarytmiczny dekrement tłumienia i częstość drgań w ruchu harmonicznym tłumionym.

31. Drgania wymuszone - równanie i rozwiązanie, zjawisko rezonansu.

32. Składanie drgań równoległych.

---