KIERUNKI NA MORZU.

W celu wyznaczenia kierunku na morzu służą dwa urządzenia:

• Żyrokompas

• Kompas magnetyczny

Mapy nawigacyjne, pozwalają na bezpośrednie naniesienie lub odczytanie tylko kierunków rzeczywistych, gdyż jedynie południki rzeczywiste ,a nie inne są naniesione na mapy.

Rozpatrując kierunki na morzu możemy wyróżnić:

1. Kurs

2. Namiar

3. Kąt kursowy

4. Kierunek wiatru

RODZAJE KURSÓW.

Kurs rzeczywisty ( KR ) - jest to kąt zawarty między północną częścią południka rzeczywistego (N_R ) a dziobową częścią linii symetrii statku.

Kurs kompasowy ( KK ) - jest to kąt zawarty między północną częścią południka kompasowego (N_K ) a dziobową częścią linii symetrii statku

Kurs magnetyczny ( KM ) - jest to kąt zawarty między północną częścią południka magnetycznego (N_K )a dziobową częścią linii symetrii statku.

Kurs żyrokompasowy (KŻ ) - jest to kąt zawarty między północną częścią południka żyrokompasowego (N_Ż ) a dziobową częścią linii symetrii statku.

N_R

N_M N_Ż N_K

Rys.1. Rodzaje kursów.

ZAMIANA KURSÓW.

Często zachodzi konieczność przeliczenia wartości poszczególnych kursów znając zależności między nimi.

N_M

N_R

N_K KK N_Ż +δ ......... KM

+ d

...........

KR

KŻ

+pż

....... d+ δ= cp

KR

KR

- d

KK ........

+cp KM

........ - δ

KR ....... KK

Poprawki: deklinacja d, dewiacja δ, cp , pż- uwzględniamy ich znaki algebraiczne

cp - całkowita poprawka kompasu magnetycznego jest sumą algebraiczną deklinacji i dewiacji. Jest kątem zawartym pomiędzy północną częścią południka rzeczywistego a północną częścią południka kompasowego

d+ δ= cp

( + ) ( - )

Zamiana kursu rzeczywistego (KR ) na kurs żyrokompasowy ( KŻ ) i odwrotnie.

Aby dokonać zamiany między kursem rzeczywistym i kursem żyrokompasowym koniecznym jest znajomość wartości poprawki żyrokompasu ( pż ).

Poprawka żyrokompasu (pż) jest kątem zawartym pomiędzy północną częścią południka rzeczywistego i północną częścią południka żyrokompasowgo

Znak poprawki żyrokompasu:

Jeżeli północna część południka żyrokompasowego odchylona jest w prawo od północnej części południka rzeczywistego , poprawka żyrokompasu przyjmuje znak plus (+).

Natomiast, jeżeli północna część południka żyrokompasowego odchylona jest w lewo od północnej części południka rzeczywistego poprawka żyrokompasu ma znak (-).

N_R

N_Ż N_Ż

(-pż) (+pż)

Rys.2. Znak poprawki żyrokompasu.

Wartość poprawki żyrokompasu.

Poprawka żyrokompasu składa się z dwóch elementów:

1. błędu stałego żyrokompasu A;

2. dewiacji prędkościowej żyrokompasu δ_ż

Znając wartość błędu stałego i wartość dewiacji prędkościowej żyrokompasu określa się pż jako ich sumę algebraiczną :

pż = A + δ_ż

A- błąd stały żyrokompasu;

δ_ż - dewiacja prędkościowa żyrokompasu

Błąd stały żyrokompasu najczęściej nie istnieje lub przyjmuje wartości małe rzędu plus , minus 1 stopień

Dewiacja prędkościowa żyrokompasu jest funkcją szerokości geograficznej, prędkości statku i kursu rzeczywitego:

• wraz ze wzrostem prędkości statku i szerokości geograficznej dewiacja prędkościowa rośnie.

• Kurs statku wpływa na znak dewiacji prędkościowej

Kursy od 000 do 090 i od 270 do 360 - znak δ_ż dodatni (+)

Kursy od 090 do 180 i od 180 do 270 - znak δ_ż ujemny (-)

Na kursach 090 i 270 δ_ż osiąga wartość 0°

Na kursach 000 i 180 δ_ż osiąga największe wartości.

Żyrokompasy nowszej generacji wyposażone są w korektor eliminujący wartość dewiacji prędkościowej żyrokompasu. Przy starszy kompasach ,aby określić wartość dewiacji prędkościowej należy skorzystać z tabeli ( ),gdzie argumentami wejściowymi są:

• Szerokość geograficzna ( Lat.)

• Kurs rzeczywisty

• Prędkość statku

KR - pż = KŻ

gdzie: pż - poprawka żyrokompasu

Kurs żyrokompasowy obliczamy jako różnicę algebraiczną między kursem rzeczywistym i poprawką żyrokompasu.

Kurs rzeczywisty równa się sumie wartości kursu żyrokompasowego i poprawki żyrokompasu z uwzględnieniem jej znaku (+) lub (-).

KŻ + pż = KR

N_R

N_Ż

(+pż)

ZAMIANA NAMIARÓW

N_M

N_R

N_K NK N_Ż +δ ......... NM

+ d

...........

NR

NŻ

+pż

....... d+ δ= cp

NR

NR

- d

NK ........

+cp NM

........ - δ

NR ....... NK

Poprawki: deklinacja d, dewiacja δ, cp , pż- uwzględniamy ich znaki algebraiczne

RODZAJE NAMIARÓW.

Namiar rzeczywisty ( NR ) - jest to kąt zawarty między północną częścią południka rzeczywistego (N_R ) a linią namiaru.

Namiar kompasowy ( NK ) - jest to kąt zawarty między północną częścią południka kompasowego (N_K ) a linią namiaru.

Namiar magnetyczny ( NM ) - jest to kąt zawarty między północną częścią południka magnetycznego (N_K )a linią namiaru.

Namiar żyrokompasowy (NŻ ) - jest to kąt zawarty między północną częścią południka żyrokompasowego (N_Ż ) a linią namiaru.

Linia namiaru jest linią łączącą obserwatora z obiektem namierzanym

ZAMIANA KURSÓW I NAMIARÓW

DANE : KK = 230º, d= 5ºW , ,NK_A= 140º, NK_B= 280º

OBLICZYĆ: KM,KR, NM,NR,

N_R

N_K

N_M

d+ δ= cp

1. Wybór dewiacji z tabeli dewiacji, gdzie argumentem wejściowym jest KK= 230 . NIE wchodzimy do tabeli namiarem kompasowym -dewiacja zależy od kursu i jest stała dla wszystkich namiarów

2. Obliczenia:

KK + δ	= 230 º = + 1º		NK + δ	= 140º = + 1º	= 280º = + 1º
KM +d	= 231º = - 5º			NM +d	= 141º = - 5º	= 281º = - 5º
KR	=226º			NR	= 136º	= 276º

KORZYSTANIE Z TABELI DEWIACJI PRZY BRAKU KURSU KOMPASOWEGO ( NP. AWARIA ŻYROKOMPASU)

Z mapy odczytujemy KDd, który odpowiada KR gdy statek nie jest dryfowany przez wiatr i nie jest znoszony przez prąd. W celu ustalenia kursu na ster ( przy awarii żyrokompasu, kursu kompasowego) należy KR poprawić o deklinację i dewiację. Deklinację uaktualnimy z mapy , dewiację należy wybrać z tabeli dewiacji. Problem polega na tym, że tabela dewiacji wykonana jest dla kursu kompasowego, a nie KR. Można zastosować dwie metody korzystania z tabeli.

I Dwukrotne wejście do tabeli dewiacji:

1. Kursem magnetycznym zamiast kursem kompasowym

(np. KR= 012º, d= -5º; KM = KR - d= 012º- (-5º) = 017º

KK	δ
000º	-2º
010º	-6º
020º	-7º
030º	-4º

Odczyt dewiacji : δ = - 6 ½ º

Obliczenie kursu kompasowego KK= KM - δ = 017º-(-6,5 º)= 023 ½ º

2. Ponowne wejście do tabeli KK i odczyt dewiacji 2: δ₂= -6º

obliczenie kursu kompasowego właściwego

KK_WŁ= KM- δ₂=017º-(-6º) = 023º

( dwukrotne wejście do tabeli dewiacji jest konieczne, kiedy zmiana dewiacji jest większa od 5º)

II Wejście do tabeli kursem magnetycznym w kolumnę KM

1. Zbudowanie w tabeli dewiacji kolumny kursów magnetycznych

KM= KK+ δ

KK	δ	KM= KK+ δ
000º	-2º	358º
010º	-6º	004º
020º	-7º	013º
030º	-4º	026º

3. Wejście do tabeli wyliczonym kursem magnetycznym

(KM = KR - d= 012º- (-5º) = 017º) i odczyt dewiacji

-7º	013º
x	017º
-4º	026º

δ = - 6º

Obliczenie kursu kompasowego KK= KM - δ =017º -(-6º)= 023º

KONTROLA DEWIACJI KOMPASU MAGNETYCZNEGO

1. Porównanie wskazań kompasu magnetycznego i żyrokompasu

2. Przecięcie linii nabieżnika

3. Wejście w nabieżnik

4. Metody astronawigacyjne- wykorzystanie ciał niebieskich

5. Wzajemne namierzanie

1- namiernik 2- podziałka 3- przegub Cardana 4- kreska kursowa 5- tarcza róży kompasowej 6- szyba	7- pływak róży kompasowej 8- czup przegubu Cardana 9- kociołek 10- membrana 11- wlew płynu 12- ciężar stateczności

www.zaglowce.ow.pl/zegluga/kompas/kompas.html

1. Porównanie wskazań kompasu magnetycznego i żyrokompasu




Odczyt z kompasów: KŻ, KK




• KK z kompasu magnetycznego




• KŻ z żyrokompasu




• d -uaktualniona deklinacja z mapy,

• pż =A+ δ_v

δ_v -dewiacja prędkościowa żyrokompasu (tabela: v, KŻ, φ),

1. błąd stały żyrokompasu ustalony wcześniej

2. Przecięcie linii nabieżnika





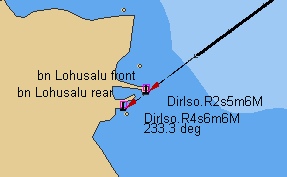
1.Wybór 2 stałych, umieszczonych na mapie, dobrze widocznych obiektów

2. Pomiar (z mapy) lub odczyt kierunku rzeczywistego na obiekty ( NR)

3.Odczyt z mapy i uaktualnienie deklinacji d







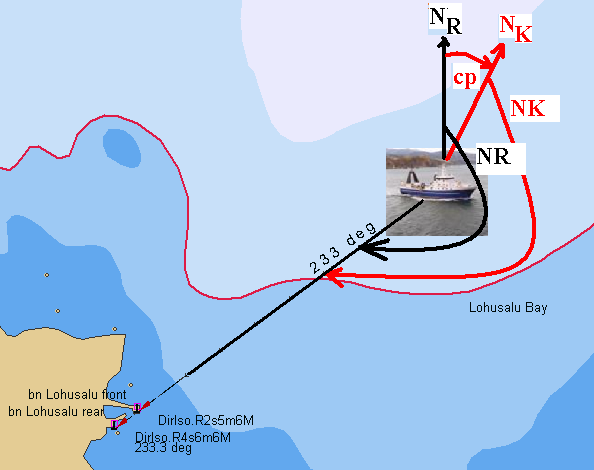
4. W momencie zamknięcia nabieżnika ( przecięcia linii prowadzącej nabieżnika) wykonanie namiaru kompasem magnetycznym ( NK) na znaki nabieżnika, które podczas pomiaru są widoczne w jednej linii

5. Obliczenie dewiacji dla trzymanego podczas pomiaru kursu kompasowego.





6. W celu określenia dewiacji dla poszczególnych kursów i opracowania tabeli dewiacji należałoby położyć statek na poszczególne kursy kompasowe

000º - w momencie przecięcia linii nabieżnika odczytać i zanotować NK

015º - w momencie przecięcia linii nabieżnika odczytać i zanotować NK

030º - w momencie przecięcia linii nabieżnika odczytać i zanotować NK

045º - w momencie przecięcia linii nabieżnika odczytać i zanotować NK itd




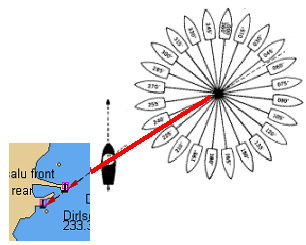
7. Następnie sporządzić tabelę i wykres dewiacji





http://www.globalsecurity.org/military/library/policy/army/fm/55-501/chap6.htm

3. Wejście w nabieżnik


Statek przemieszczając się po linii prowadzącej nabieżnika widzi oba znaki w jednej linii ( nabieżnik zamknięty; KDd=Ldg). Jeżeli występuje prąd i wiatr, to w celu utrzymania się w linii prowadzącej koniecznym jest przeciwdziałanie znoszeniu przez prąd i dryfowaniu wskutek działania wiatru, stąd w takich warunkach KR nie będzie równał się KDd, a i KR będzie różny od NR na nabieżnik.

W celu kontroli dewiacji:

• wykonujemy NK na znaki widoczne w jednej linii,

• odczytujemy KK,

• odczytujemy NR na znaki i deklinację z mapy.

Można również skontrolować błąd stały żyrokompasu (A) wykonując NŻ.





4. Metody astronawigacyjne- wykorzystanie ciał niebieskich

1. wszystkie zidentyfikowane ciała niebieskie ( słońce, księżyc, planety, gwiazdy) do wysokości 25-30˚

2. wschody i zachody słońca

































Należy:

• namierzyć ciało niebieskie kompasem magnetycznym (NK )

• odczytać kurs kompasowy z kompasu magnetycznego (KK)

• uaktualnić deklinację z mapy (d)

• określić azymut na ciało niebieskie wykorzystując metody i pomoce astronawigacyjne ( Az )

Azymut (Az) = namiar rzeczywisty (NR)




5. Wzajemne namierzanie

• Ze statku A, posiadającego dobrą tabelę dewiacji wykonujemy NK na statek B, dla którego chcemy określić dewiację.

NK_AB=070˚

• Statek B wykonuje jednocześnie namiar kompasowy na statek A

NK_BA =259˚

Kontr-namiar kompasowy ≠ NK+180˚, gdyż dewiacja dla obu kompasów ma różne wartości i zależy od kursów. Każdy statek ma własną tabelę dewiacji.

NK_AB = 070˚

+ δ_A = + 5˚

NM_AB = 075˚

+180˚ ( deklinacja w akwenie jednakowa- można zamienić na kontr-namiar)

NM_BA = 255˚

-NK_BA = 259˚

δ_B = - 4˚ dla KK na którym leżał statek B w momencie pomiaru.





























































Gdyby namierzanie wykonywane było kompasem usytuowanym z dala od elementów ferromagnetycznych ( poza statkiem) wówczas dewiacja tego kompasu równałaby się zeru, a więc NK_AB=NM_AB










http://www.globalsecurity.org/military/library/policy/army/fm/55-501/chap6.htm

6

KK

KŻ

KM

KR

KŻ

KR

KK

KM

KR

KŻ

pż

d

δ

cp

KR

KM

KK

d

δ

cp

pż

δ

d

NK

NM

NR

NŻ

NR_AB

N_R

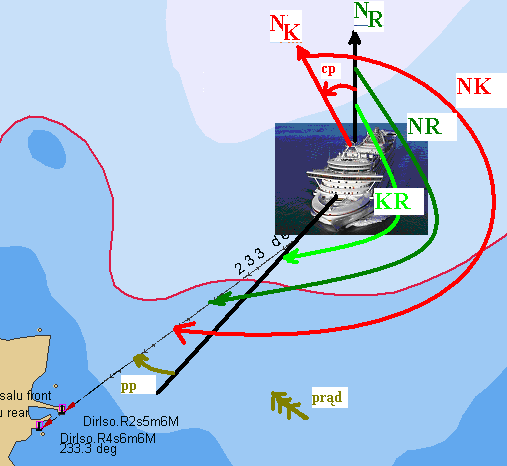
KDd = 233º ( z mapy)

- pp = + 5º

KDw = 228º

-pw = 0º

KR = 228º ≠ NR = 233º




NR = 233º

- NK = 250º

cp = -17º

-d = - 20º

δ = +3 º

NR = 233º

- NŻ = 234º

pż = - 1º

-δ_v = - 1º( z tabeli)

A = 0º




NR = 233º

- NK = 223º

cp = +10º

-d = +1 6º

δ = - 6 º

NR = 087

- NK = 100

cp = -13

-d = - 10

δ = - 3 dla KK










cp

NK

N_K

N_R

A_Z

KŻ = 320º

+pż = -1

KR = 319º

-KK = 330º

cp = - 11º

- d = - 6º

δ = - 5˚

KR

NR

NM

NK

d

δ

KK

NR_BA

cp

N_R

N_M

N_M

d

d

NM_AB

NM_BA

N_K

δ

N_K

NK_AB

NK_BA

δ

---