Tematy teoretyczne na egzamin z

MECHANIKI II

Kinematyka

1. Ruch kulisty (definicja, prędkość i przyspieszenie, aksoidy, dowód, że można traktować jako chwilowy ruch obrotowy).

Ruch kulisty - jeden punkt ciała sztywnego nieruchomy - środek ruchu kulistego

(3 stopnie swobody).

Ruchem kulistym nazywamy taki rodzaj ruchu, w którym jeden punkt ciała sztywnego pozostaje nieruchomy. Na przykład ruchem kulistym poruszać się może aparat fotograficzny, umocowany na przegubie kulistym statywu.

Prędkość:

(prędkość kątowa obrotu własnego)

(prędkość kątowa precesji)

(prędkość nutacji)

Przyspieszenie:

- przyspieszeni obrotowe

- przyspieszenie doosiowe

- ma kierunek niezależny od

-prędkość końca wektora

Aksoidy:

Miejsce geometryczne chwilowych osi obrotu w ruchu kulistym ciała sztywnego nazywamy aksoidą. Chwilowe osie obrotu w układzie ruchomym tworzą aksoidę ruchomą, natomiast w układzie stałym - aksoidę stałą (nieruchomą).

Ruch kulisty ciała sztywnego można traktować jako toczenie się bez poślizgu aksoidy ruchomej po aksoidzie stałej.

Dowód, że ruch kulisty możemy traktować jako chwilowy ruch obrotowy:

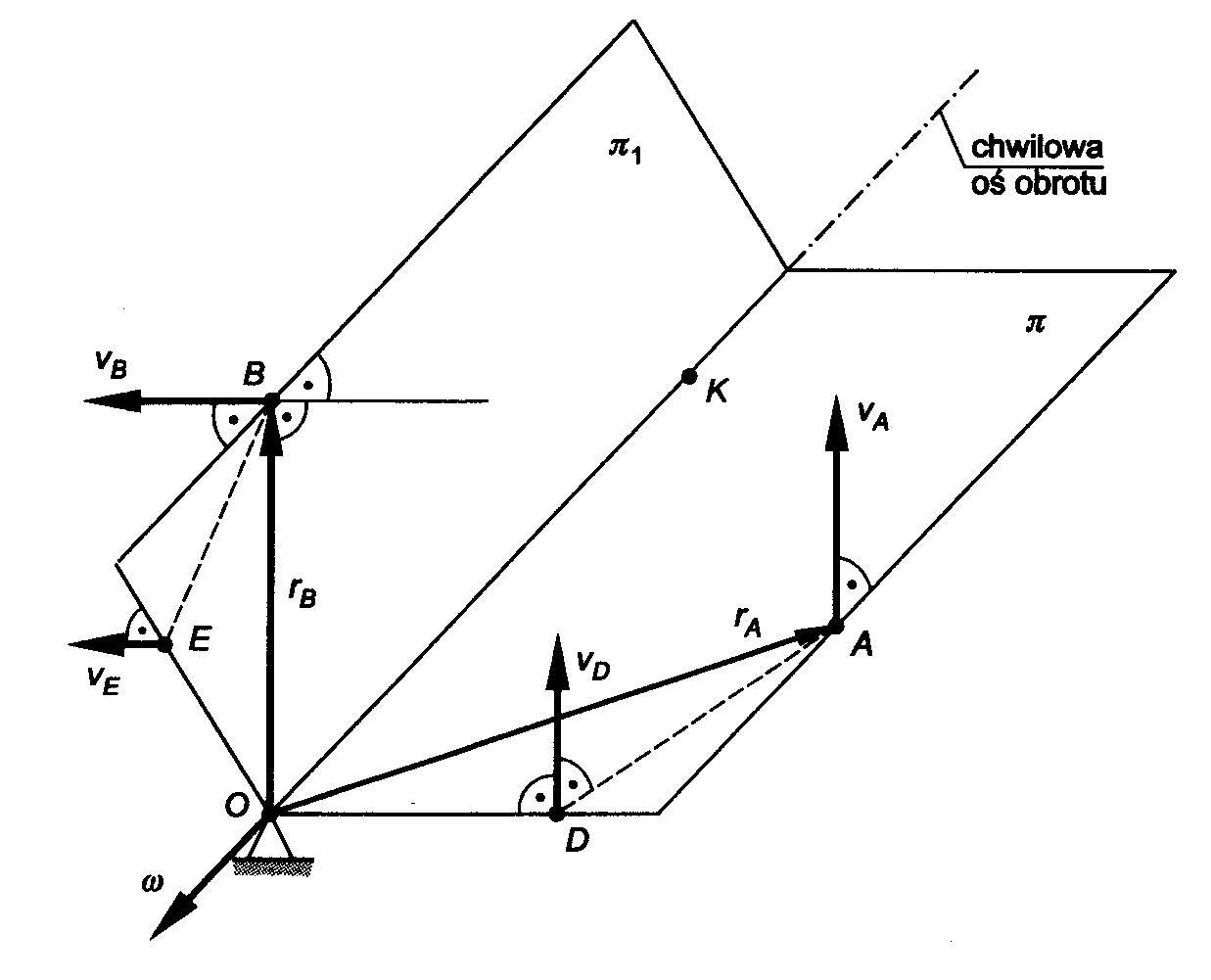
Dane:

2. Wyprowadzić wzory na prędkość i przyspieszenie punktu w ruchu złożonym (przyspieszenie Coriolisa).

Prędkość:

- prędkość bezwzględna

- prędkość unoszenia

- prędkość względna

po podstawieniu otrzymujemy

Przyspieszenie:

Przyspieszenie Coriolisa:

2. Swobodny spadek ciał z uwzględnieniem oporu powietrza.

k - współczynnik oporu powietrza

- ciężar właściwy powietrza (gazu), F - pole rzutu przekroju poprzecznego ciała na płaszczyznę prostopadłą do kierunku ruchu, g - przyspieszenie ziemskie, f - współczynnik zależny od kształtu ciała, np., f = 0,005 - dla kształtu kropli wody, f = 1,3 - dla płytki kwadratowej, ustawionej prostopadle do kierunku ruchu.

Po podstawieniu otrzymujemy

Zgodnie z tym równaniem prędkość spadania stale rośnie, aż osiągnie pewną wartość graniczną, przy której przyspieszenie
staje się równe 0. Tę wartość oznaczamy c i nazywamy prędkością graniczną. Wówczas otrzymujemy:

po podstawieniu otrzymujemy

, skąd

a po rozdzieleniu zmiennych

.

Aby to równanie doprowadzić do postaci całkowalnej, zastosujemy tożsamościowe podstawienie:

,

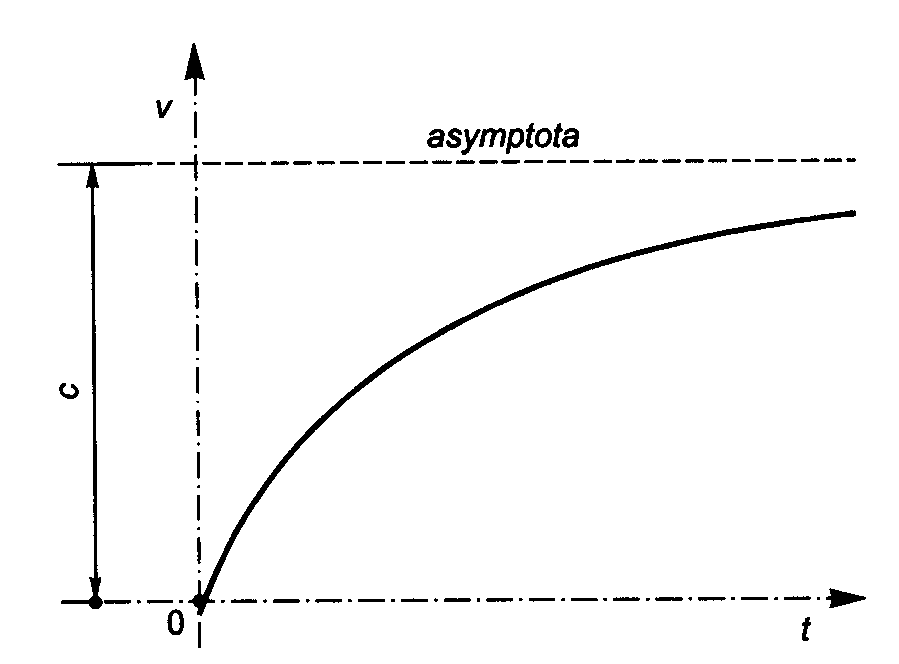
po scałkowaniu

t = 0, A = 0

, lub

4. Pęd punktu i układu materialnego, (definicja, twierdzenie o pochodnej względem czasu, zasada zachowania pędu)

Pęd punktu materialnego:

Pędem (lub ilością ruchu) punktu materialnego nazywamy iloczyn masy punktu przez jego prędkość.

po zróżniczkowaniu zależności względem czasu:

i podstawieniu zależności:

,

otrzymujemy

Pochodna geometryczna wektora pędu jest równa sile działającej na dany punkt materialny.

Pęd układu materialnego:

równanie wektorowe rzutuje na oś x

Pęd (ilość ruchu) układu materialnego jest równy iloczynowi masy całego układu przez prędkość środka masy.

Twierdzenie o pochodnej względem czasu:

Zasada zachowania pędu:

Pęd układu izolowanego jest stały.

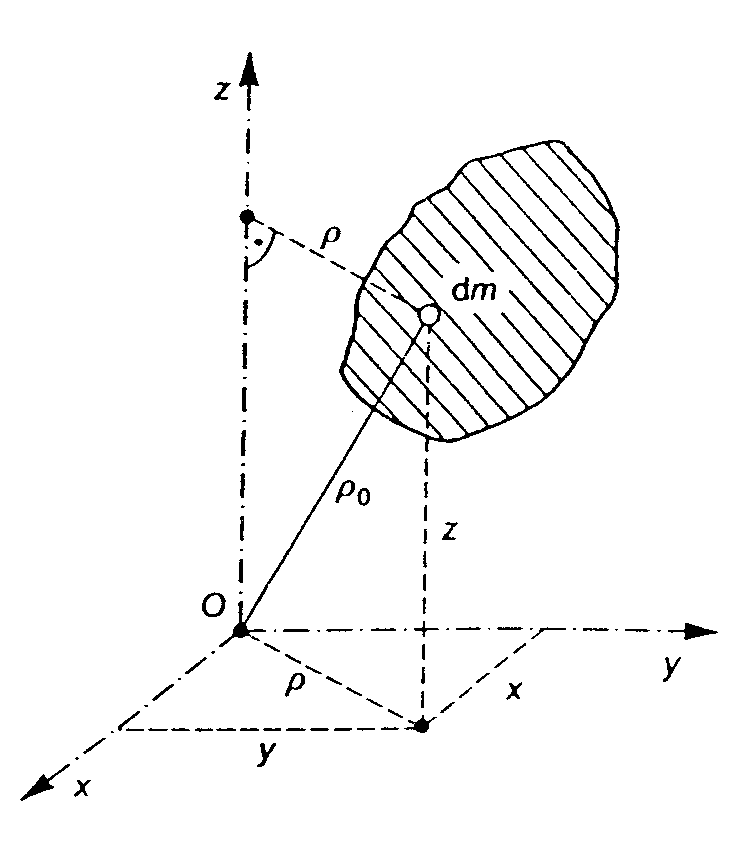
5. Momenty bezwładności względem płaszczyzny, osi, punktu. Moment bezwładności odśrodkowy. Twierdzenie Steinera. Obrót osi.

Moment bezwładności względem płaszczyzny

Moment bezwładności względem osi

,

Moment bezwładności względem punktu

Moment bezwładności odśrodkowy

Twierdzenie Steinera

,

,

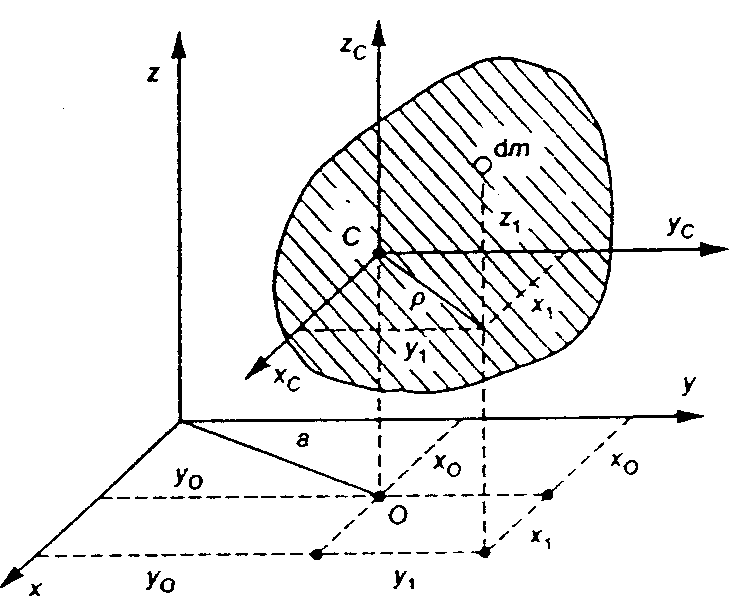
zgodnie ze wzorem

Wzory na określenie współrzędnych środka masy w zapisie całkowym przyjmują postać

po podstawieniu zależności otrzymujemy wzór Steinera

Moment bezwładności względem dowolnej osi z jest równy sumie momentu bezwładności względem równoległej osi centralnej i iloczynu masy ciała przez kwadrat odległości między osiami.

6. Moment bezwładności walca, kuli, prostopadłościanu i stożka.

Walec:

,

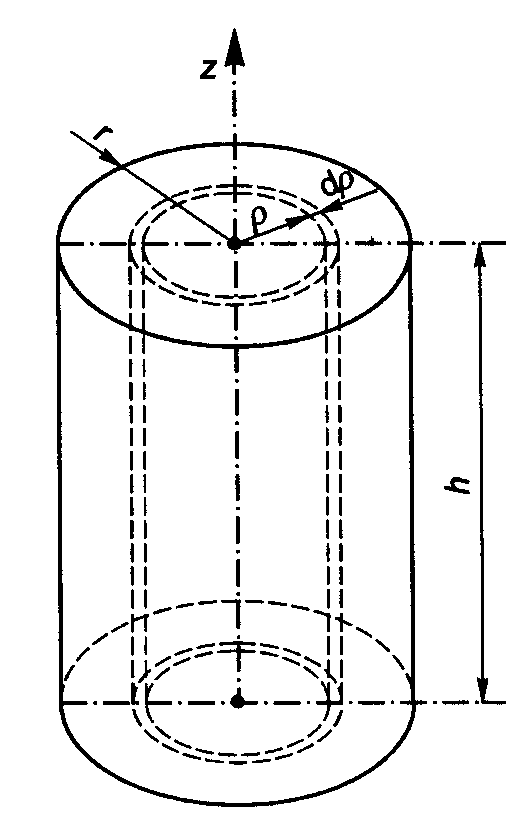
- ciężar właściwy

Wydzielając z otrzymanego wyrażenia masę walca

otrzymujemy

Kula:

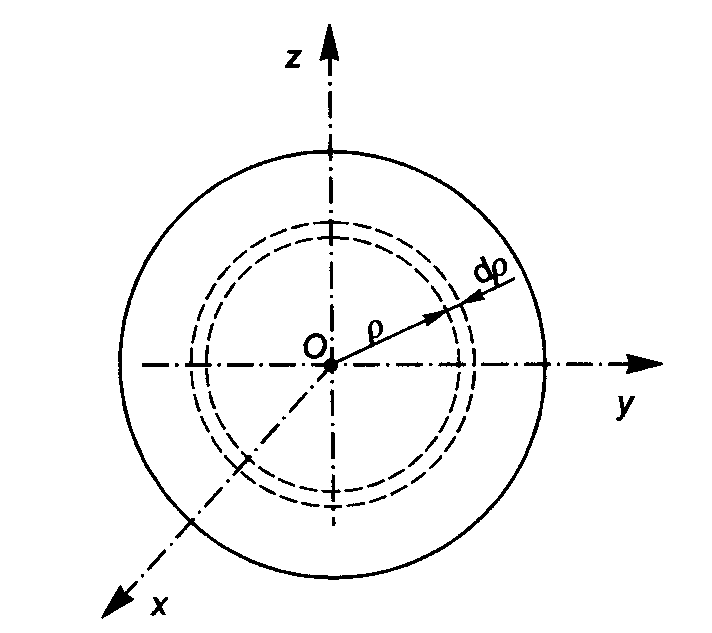
po wydzieleniu masy kuli:
, otrzymujemy

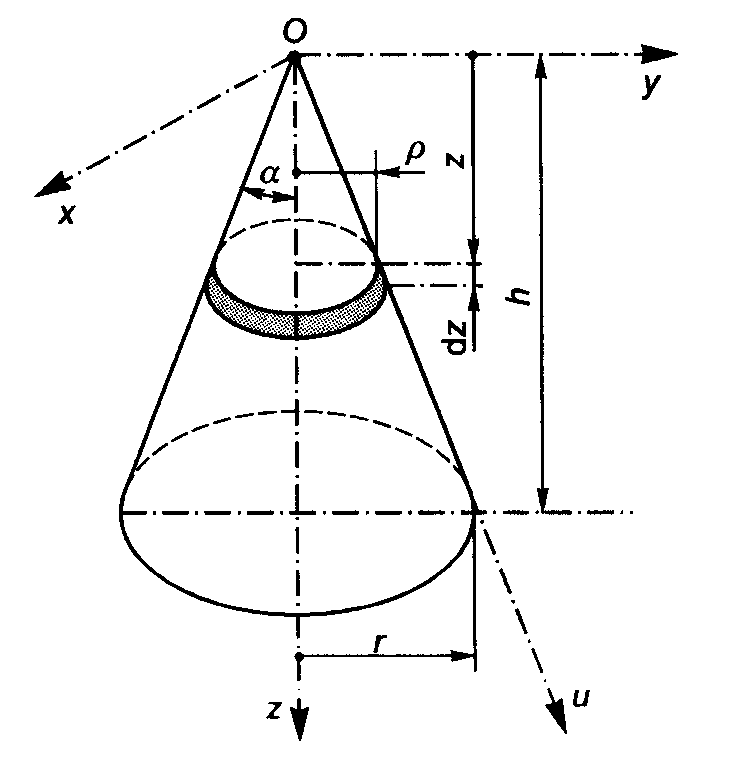
Stożek:

po wyodrębnieniu masy stożka

,

.

7. Kręt punktu materialnego. Twierdzenie o pochodnej krętu względem czasu.

Kręt punktu materialnego:

Twierdzenie o pochodnej krętu względem czasu:

10. Twierdzenie Koeniga o energii kinetycznej układu mechanicznego oraz ciała sztywnego.

Energia kinetyczna układu mechanicznego:

Twierdzenie Koeniga:

Energia kinetyczna układu materialnego równa jest sumie energii kinetycznej punktu o masie całego układu i prędkości równej prędkości środka masy oraz energii kinetycznej tego układu w jego ruchu względem środka masy.

Energia kinetyczna ciała sztywnego:

- w ruchu postępowym v = const.

- w ruchu obrotowym dookoła stałej osi

- w ruchu płaskim z twierdzenia Koeniga

14. Efekt żyroskopowy. Zastosowanie żyroskopów.

Efekt żyroskopowy:

Chcemy obrócić dookoła osi y:

w płaszczyźnie x y

Zastosowanie żyroskopów:

Przykładem zastosowania jest busola żyroskopowa, (która wskazuje kierunek północny, wykorzystując ruch obrotowy ziemi wokół osi), stabilizator okrętowy.

15. Uderzenie (klasyfikacja, współczynnik restytucji). Środek uderzenia.

Linia uderzenia: wspólna normalna do powierzchni styku ciała.

Uderzenie proste, prędkość względna punktu uderzenia leży na linii uderzenia lub ukośne jeżeli nie leży.

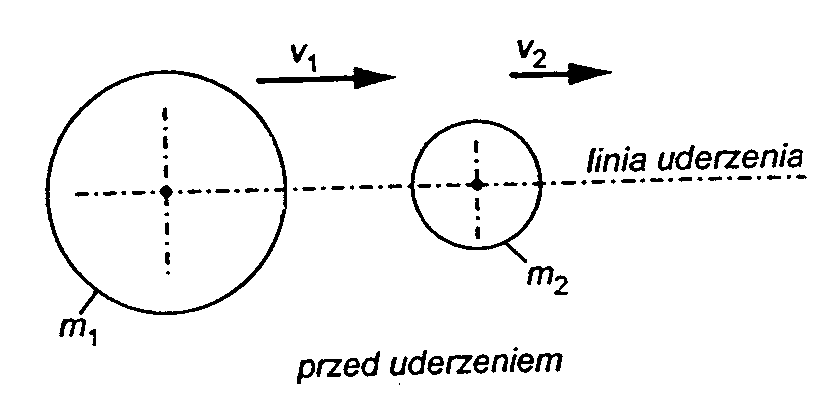
Uderzenie centralne, linia uderzenia przechodzi przez środek masy lub mimośrodowe jeżeli nie leży.

1) zasada zachowania pędu:

2) wzór Newtona

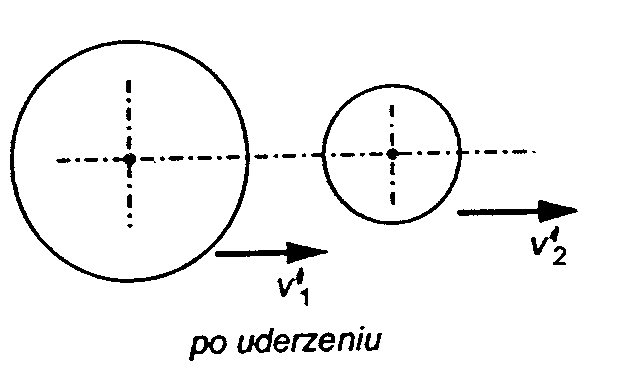
k - współczynnik restytucji

Uderzenie o ścianę:

- idealnie sprężyste

- idealnie plastyczne

Środek uderzenia:

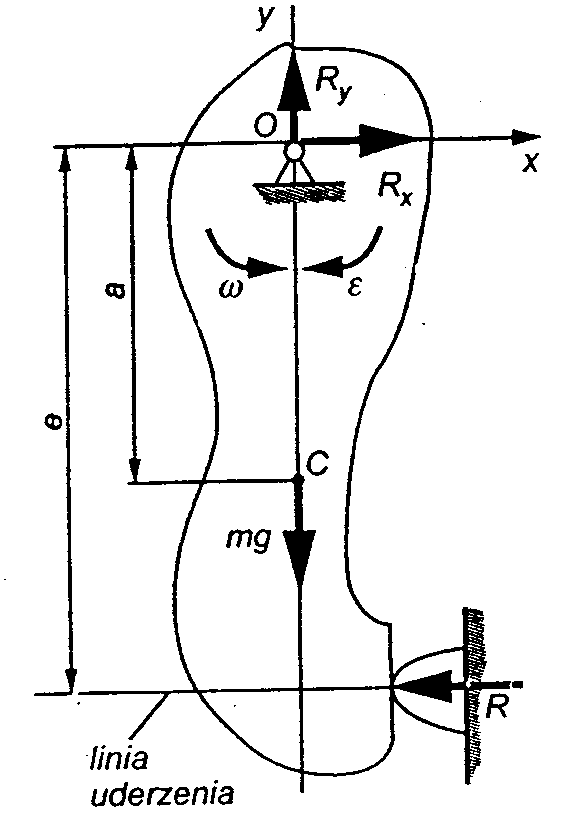
- prędkość kątowa tuż przed uderzeniem

- przyspieszenie kątowe w czasie 1 fazy uderzenia

- przyspieszenie środka masy w czasie 1 fazy

Dynamiczne równanie ruchu obrotowego w czasie 1 fazy:

Dynamiczne równanie ruchu ciała (w kierunku osi x):

gdy

16. Zasada prac przygotowanych. Twierdzenie Dirichleta. Analiza stanów równowagi.

- przesunięcie przygotowane (wirtualne) - dowolnie małe przesunięcie

zgodne z nałożonymi więzami.

wektor
leży w płaszczyźnie stycznej

A. Zasada prac przygotowanych dla punktu materialnego

Jeżeli punkt materialny jest w równowadze, to praca przygotowana sił zewnętrznych i reakcji jest równa zeru.

B. dla układu materialnego

C. dla więzów idealnych

Równowaga w potencjalnym polu sił

Zasada prac przygotowanych dla więzów idealnych, gdy pracę wykonują siły określone potencjałem:

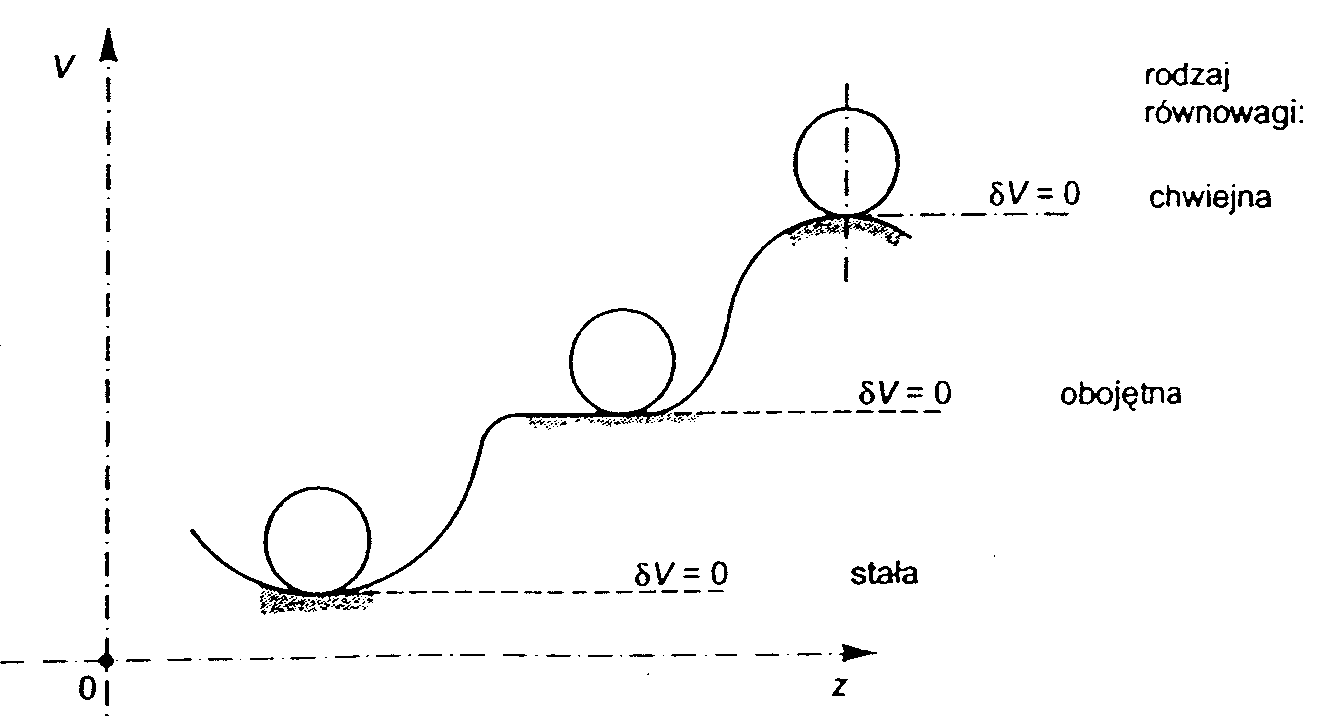
Zasada Dirichleta

Gdy układ materialny znajduje się w równowadze w zachowawczym polu sił, wówczas położenie w którym energia potencjalna osiąga minimum jest położeniem równowagi stałej.

tor względny

Tor unoszenia

tor bezwzględny

- wariacja funkcji V

---