Imię i nazwisko:	Ćwiczenie nr C5 Wyznaczanie ciepła właściwego metodą kalorymetryczną.
Kierunek i rok:	Ocena z kolokwium: ....................................... data ....................... podpis...........................	Ocena ze sprawozdania: ....................................... data ....................... podpis...........................	Ocena końcowa: ....................................... data ....................... podpis...........................
Nazwisko prowadzącego zajęcia:

Ciepło i pojemność cieplna.

Ciepło (cieplny przepływ energii) Q - ta część energii wewnętrznej ∆U, którą ciało o temperaturze wyższej przekazuje ciału o temperaturze niższej bez wykonywania pracy W

Q = ∆U, gdy W = 0.

Jednostką ciepła jest kaloria, cal - pozaukładowa jednostka energii używana przy określaniu ilości ciepła, równa ilości ciepła, jakiej potrzeba do ogrzania 1g czystej wody o 1˚C. 1cal = 4,1868J.

Ciepło właściwe substancji c - stosunek ilości ciepła Q pobranego przez ciało do iloczynu masy m substancji i przyrostu jego temperatury ∆T wywołanego pobraniem tego ciepła:

Jednostką ciepła właściwego jest dżul na kilogram i kelwin:

.

Jest to ciepło właściwe ciała o masie 1 kg, którego temperatura wzrasta o 1 K po pobraniu przez nie ciepła w ilości 1 J.

Ciepło molowe c_m - stosunek ilości ciepła Q pobranego przez ciało do iloczynu liczności materii (wyrażonej przez liczbę moli) n ciała i przyrostu temperatury ∆T wywołanego jej pobraniem:

Ciepłem molowym posługuje się głównie w przypadku gazów. Ponieważ gazy charakteryzują się dużą ściśliwością istotny jest sposób przepływu ciepła (ciepło molowe zależy od przemiany termodynamicznej). Z tego względu posługujemy się ciepłami molowymi:

• ciepło molowe przy stałej objętości (dla przemiany izochorycznej):

• ciepło molowe przy stałym ciśnieniu (dla przemiany izobarycznej):

Jednostką ciepła molowego jest dżul na mol i kelwin:

Jest to ciepło molowe 1 mola substancji, którego temperatura wzrasta o 1 K po pobraniu przez niego 1 J ciepła.

Zależności między ciepłem molowym przy stałej objętości c_v i ciepłem molowym przy stałym ciśnieniu c_p:

Równanie Mayera - określa związek między c_p, c_v i R mówiący, że dla każdego gazu doskonałego różnica ciepła molowego przy stałym ciśnieniu i ciepła molowego przy stałej objętości jest równa uniwersalnej stałej gazowej:

c_p jest większe od c_v, ponieważ przy stałym ciśnieniu (a zmiennej objętości) nie cała energia dostarczona na sposób ciepła ma wpływ na wzrost temperatury gazu - część energii zostaje zużyta na wykonanie pracy.

Pojemność cieplna C - stosunek ilości ciepła Q dostarczonego ciału (układowi), do zmiany jego temperatury ∆T:

Pojemność cieplna C ciała o masie m zawierającego n moli substancji jest równa:

c - ciepło właściwe,

c_m - ciepło molowe substancji tego ciała.

Pierwsza zasada termodynamiki:

Zasadę zachowania energii można sformułować ogólnie w sposób następujący:

W układzie odosobnionym, w którym zachodzą dowolne zjawiska mechaniczne, cieplne, elektryczne, magnetyczne, chemiczne, czy też przemiany jądrowe, nie można w żaden sposób zmienić całkowitej energii układu. Jeśli natomiast mogą zachodzić wymiany energii układu z otoczeniem, to przyrost (lub ubytek) całkowitej energii układu równa się doprowadzonej z zewnątrz (lub odprowadzonej na zewnątrz) energii.

Weźmy pod uwagę dowolny układ. Układ ten ma energię w różnych postaciach: energie kinetyczną, potencjalną, chemiczna, elektryczną, magnetyczną lub jądrową. W dalszym ciągu będziemy abstrahować od energii kinetycznej, gdyż będziemy rozpatrywać układ znajdujący się w spoczynku. Wszystkie pozostałe energie będziemy obejmować nazwą energii wewnętrznej układu U. Pojęcie energii wewnętrznej układu zostało wprowadzone po raz pierwszy do nauki przez Kelwina. Możemy teraz sformułować matematycznie pierwszą zasadę termodynamiki. Oznaczymy przez Q ciepło dostarczone naszemu układowi z zewnątrz, pracę zaś dostarczoną z zewnątrz - przez L, wówczas, jeśli U₁ oznacza energię wewnętrzną układu w stanie początkowym, U₂ zaś jego energie w stanie końcowym, mamy:

Przy czym energia wewnętrzna ma dla każdego ze stanów jednoznacznie określoną wartość.

Zauważymy, że stan układu w najprostszym przypadku (np. stanu gazu)jest w zupełności określony przez podanie np. wartości temperatury i objętości układu; dla układów bardziej złożonych potrzebne są jeszcze wartości dodatkowych parametrów.

W powyższym równaniu zawarta jest odpowiedź, że zmiana energii nie zależy od drgii, po której przechodzimy ze stanu 1 do 2.

Jeśli rozpatrujemy bardzo małą zmianę układu, przy której energia wewnętrzna doznaje zmiany o dU, to pierwszą zasadę termodynamiki można wyrazić równaniem:

przy czym dU jest różniczką zupełną. Jednakże δQ i δL nie są różniczkami zupełnymi, co zaznaczyłam przez odrębne oznaczenie. Wynika stąd, że w poprzednim wzorze Q i L zależą od drogi, jaką układ nasz przeprowadzamy ze stanu 1 do 2. w związku z tym podkreślić należy, że ciepło nie jest rodzajem energii. Wymiana ciepła miedzy układami - podobnie jak praca wykonywana przez jeden układ nad drugim - jest sposobem przekazywania energii, a w związku z tym praca i ciepło charakteryzują nie stan układu, a proces, jakiemu poddajemy układ. Warto zaznaczyć, że terminologia dotycząca procesów termicznych i używana dotychczas pochodzi jeszcze z okresu panowania teorii cieplika i dlatego może być myląca.

Tak więc bilans cieplny możemy zdefiniować:

Bilans cieplny - zestawienie ilości ciepła doprowadzonego do układu i ilości ciepła odprowadzonego z układu.

Jeżeli między ciałami o różnych temperaturach, które są w kontakcie termicznym między sobą i tworzą układ odizolowany termicznie od otoczenia, następuje wymiana energii tylko na sposób ciepła, to jej ilość Q jest równa (co do wartości) przyrostowi energii wewnętrznej ∆U_n ciała o temperaturze niższej od pozostałych i jest równa zmniejszeniu energii wewnętrznej ∆U_w ciał o temperaturze wyższej. Powyższy warunek można zapisać w postaci:

.

Prawo Lenza-Joule'a:

Przepływ prądu elektrycznego przez przewodniki jest połączony z przemianą energii elektrycznej w energię cieplną. Zjawisko to można wyjaśnić na podstawie teorii elektronowej prądu. Swobodne elektrony, trwające w ruchu uporządkowanym, ustawicznie zderzają się z innymi cząstkami przewodnika (jonami siatki krystalicznej metalu) i oddają im część energii kinetycznej nagromadzonej przez elektrony podczas ich ruchu w polu elektrycznym przewodnika. Wskutek tych zderzeń wzmagają się drgania siatki krystalicznej przewodnika powodujące wzrost jego temperatury.

Jeśli przez przewodnik lub odbiornik o oporności R płynie prąd o natężeniu I, to na zasadzie zachowania energii dostarczona do tego przewodnika energia elektryczna zmienia się w całości na energię cieplną. Wartość tej energii znajdujemy ze wzoru:

podstawiając w nim na podstawie prawa Ohma U = IR:

wartość tej energii wyrażona jest w dżulach (watosekundach). Chcąc wyrazić wartość tej energii w jednostkach energii cieplnej posługujemy się elektrycznym równoważnikiem cieplnym wyznaczonym przez Lenza-Joule'a:

albo:

A zatem ilość ciepła wydzielona w przewodniku o oporności R, przez który płynie prąd o natężeniu I w ciągu czasu t, wyrazi się wzorem:

Q - ilość ciepła w kaloriach,

I - natężenie prądu w A,

t - czas w s.

Wzór ten wyraża prawo Lenza-Joule'a wykryte jednocześnie przez uczonych rosyjskiego Lenza i angielskiego Joule'a.

Z prawa Lenza-Joule'a wynika, że ilość wytworzonego ciepła w przewodniku jest wprost proporcjonalna do kwadratu natężenia prądu, oporności przewodnika i czasu trwania przepływu prądu.

Wartość skuteczna natężenia prądu, napięcia i siły elektromotorycznej:

Posługiwanie się w praktyce wartościami chwilowymi bądź szczytowymi natężenia prądu, napięcia, czy też siły elektromotorycznej sprawia trudności i komplikuje obliczenia. Wprowadzono wobec tego pojęcie wartości skutecznych natężenia prądu, napięcia i sem, którymi najczęściej posługujemy się w elektrotechnice.

Wartością skuteczną natężenia prądu zmiennego nazywamy taki umyślony prąd stały, który płynąc w obwodzie o stałej oporności R wytworzy w ciągu okresu T tę samą ilość ciepła, jaką w tymże czasie wytworzy prąd zmienny. Wartości skuteczne oznaczać będziemy dużymi literami.

Wyznaczymy zależno0ść wartości skutecznej od wartości szczytowej natężenia prądu sinusoidalnie zmiennego. Przypuśćmy, że w obwodzie o oporności R płynie prąd stały o natężeniu I. Po upływie czasu T (trwania jednego cyklu prądu zmiennego) w obwodzie tym wydzieli się pewna ilość ciepła, którą możemy wyznaczyć na podstawie prawa Joule'a-Lenza:

Jeśli do tego samego obwodu doprowadzimy prąd zmienny, to będzie on również wytwarzał ciepło. Chcąc wyznaczyć ilość ciepła wytworzoną przez prąd zmienny natrafimy na trudność polegającą na tym, że w rozpatrywanym obwodzie natężenie prądu w każdej chwili ma inną wartość. Wobec tego na poniższym wykresie sinusoidy prądu:

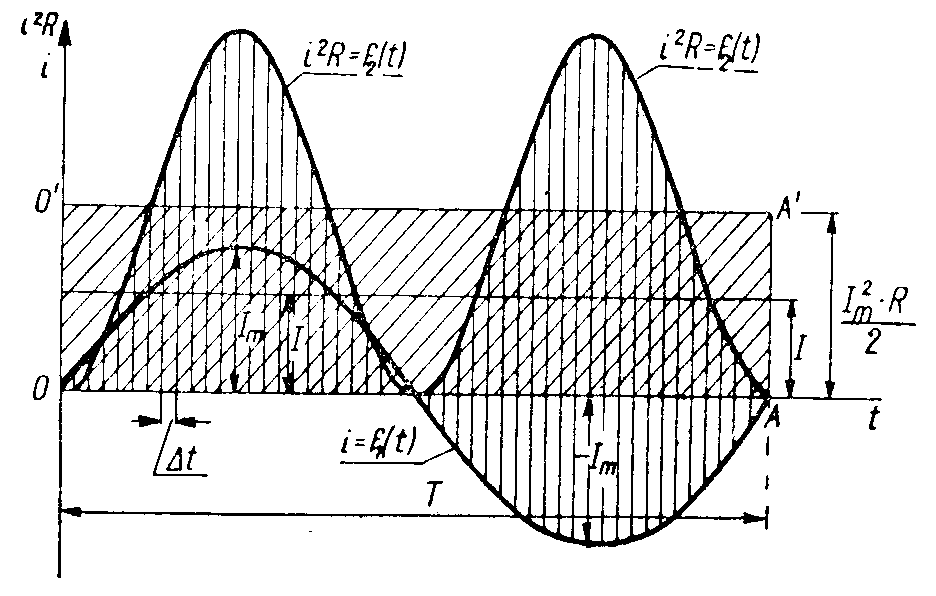
dzielimy okres T na możliwie dużą liczbę odcinków czasu tak małych, aby można było uważać, że w ciągu takiego odcinka czasu oznaczonego przez ∆t wartość chwilowa prądu i jest stała.

Wówczas ilość ciepła wydzielonego w czasie ∆t wyniesie:

Sumując te wydzielone ilości ciepła w ciągu całego okresu T otrzymamy ilość ciepła wytworzonego przez prąd zmienny w ciągu jednego okresu T:

I - wartość skuteczna prądu zmiennego.

Zależność wartości skutecznej od szczytowej wyznaczymy metodą wykreślną. Na wyżej zamieszczonym rysunku przedstawiono wykres i = f₁(t) prądu zmiennego sinusoidalnego. Na osi czasu (odciętych) dokonujemy podziału okresu T na odstępy ∆t. Następnie na rzędnych otrzymanych z podziału rozpoczynając od punktu zerowego odkładamy wartości i²R. końce rzędnych utworzą krzywą i²R = f₂(t), która przedstawia przebieg zmienności mocy prądu zmiennego wydzielonej w postaci ciepła. Krzywa ta jest również sinusoidą zawierającą jedynie rzędne dodatnie. Pole ograniczone tą krzywą i osią poziomą przedstawia ilość energii prądu zmiennego wydzielonej w postaci ciepła w ciągu okresu T. Podzielimy wartość szczytowa krzywej na pół i przez punkt podziału poprowadzimy prostą O'A', równoległą do osi czasu (odciętych). Kreśląc następnie rzędne w punktach O i A otrzymamy prostokąt O A A'O'. Pole tego prostokąta jest równe polu ograniczonemu krzywą i²R = f₂(t) i osią czasu (odciętych). A zatem pole prostokąta wyraża również ilość energii prądu zmiennego wydzielone w postaci ciepła w obwodzie w ciągu okresu T. Wysokość prostokąta I_m²R/2 przedstawia średnią mc prądu zmiennego wydzieloną w postaci ciepła w ciągu okresu T.

Wobec podanej wartości skutecznej prądu zmiennego możemy napisać:

i wreszcie:

otrzymaliśmy zależność pomiędzy wartością skuteczną prądu zmiennego, a jego wartością szczytową. Taka sama zależność zachodzi w odniesieniu do wartości skutecznych napięcia i siły elektromotorycznej prądu sinusoidalnie zmiennego:

podkreśla się, że liczba √2 = 1,42 wyrażająca stosunek między wielkościami szczytową i skuteczną jest właściwa jedynie dla wielkości o przebiegu sinusoidalnie zmiennym. Przyrządy przeznaczone do pomiarów prądu zmiennego wskazują wartości skuteczne.

Tabela wyników pomiarów:

Lp.	mk [kg]	m [kg]	mw [kg]	U [V]	I [A]	t [s]	Tp [K]	Tk [K]	Q [J]	Q/∆T [J/K]
1	0,0688	0,2746	0,2058	12,00	2,30	379,32	296,15	306,15	10469,232	1046,9232
2			0,2647	0,1959	12,25	2,20			372,00			10025,400	1002,5400
3			0,2771	0,2083	12,50	2,15			378,00			10158,750	1015,8750
4			0,3231	0,2543	12,50	2,10			436,20			11450,250	1145,0250
5			0,3837	0,3149	12,50	2,10			545,40			14316,750	1431,6750
Wartości średnie		0,30464	0,23584	12,35	2,17	422,184	∆T = 10 K		11284,0764	1128,40764

∆m_k; ∆m; ∆m_w = ± 0,0005 kg

Wyznaczam niepewność pomiaru Q/∆T metodą pochodnej logarytmicznej:

∆t = ± 0,2 s

dT = ± 0,5 K

Zakres I = 5A; Klasa I = 0,5; Działka = 0,1

∆I = ± 0,125A

Zakres U = 30V; Klasa U = 0,5; Działka = 0,5

∆U = ± 0,65V

Wyznaczam niepewność procentową:

Np = 13,87%

Ponieważ zależność Q/∆T = f(m_w) jest liniowa można zastosować metodę regresji liniowej.

Lp.	mw [kg]	Q/∆T [J/K]	mw^2 [kg]	(Q/∆T)^2 [J/K]	mw · (Q/∆T) [J/K]
1	0,2058	1046,9232	0,04235364	1096048,187	215,4567946
2	0,1959	1002,5400	0,03837681	1005086,452	196,3975860
3	0,2083	1015,8750	0,04338889	1032002,016	211,6067625
4	0,2543	1145,0250	0,06466849	1311082,251	291,1798575
5	0,3149	1431,6750	0,09916201	2049693,306	450,8344575
n = 5	Σ mw = 1,1792	Σ (Q/∆T) = 5642,0382	Σ mw^2 = 0,28794984	Σ (Q/∆T)^2 = 6493912,212	Σ mw · (Q/∆T) = 1365,475458

Wyznaczam ciepło właściwe:

c_w =3539,764862 J/kg·K

Wyznaczam pojemność cieplną:

C = 293,5894993 J/K

Wyznaczam odchylenie standardowe od średniej wartości ciepła właściwego:

S_cw = 368,2900434 J/kg·K

Wyznaczam odchylenie standardowe od wartości średniej pojemności cieplnej:

S_C = 88,38191282 J/K

Wyznaczam punkty do wykreślenia prostej teoretycznej o równaniu:

Q/∆T = 3539,764862 · m_w + 293,5894993

Za m_w przyjmuje wartości:

m_w = 0,18 kg

Q/∆T = 930,7471745 J/K

m_w = 0,32 kg

Q/∆T = 1426,314255 J/K

Wyznaczam proste (Q/∆T)₁ i (Q/∆T)₂:

(Q/∆T)₁ = 3908,054905 · m_w + 381,9714121

(Q/∆T)₂ = 3171,474819 · m_w + 205,2075865

Wyznaczam punkty do wykreślenia prostych (Q/∆T)₁ i (Q/∆T)₂:

Za m_w przyjmuje wartości:

m_w = 0,18 kg

(Q/∆T)₁ = 1085,421295 J/K

m_w = 0,32 kg

(Q/∆T)₁ = 1632,548982 J/K

Za m_w przyjmuje wartości:

m_w = 0,18 kg

(Q/∆T)₂ = 776,0730538 J/K

m_w = 0,32 kg

(Q/∆T)₂ = 1220,079528 J/K

WNIOSKI I UWAGI:

Celem ćwiczenia było wyznaczenie ciepła właściwego wody i pojemności cieplnej kalorymetru.

Po wykonaniu pomiarów i dokonaniu obliczeń otrzymałam następujące wyniki:

Ciepło właściwe wody wynosi c_w= 3539,764862 J/kg*K

Pojemność cieplna kalorymetru C = 293,5894993 J/K

Porównując otrzymane w ćwiczeniu wartości ciepła właściwego wody z podanymi w tablicach:

Ciepło właściwe wody c_w= 4200 J/kg*K.

Można powiedzieć, że uzyskane wyniki nie pokrywają się z tablicowymi, jednak rząd wielkości jest zachowany. Może to być spowodowane niedokładnością przeprowadzonych pomiarów, wadami sprzętu pomiarowego, a także czynnikami niezależnymi od człowieka, jak warunki otoczenie, czy drgania budynków.

---