Akademia Techniczno-Humanistyczna

w Bielsku-Białej

Ćwiczenie 78

Wyznaczanie długości fali świetlnej metodą pierścieni Newtona.

WBiM - semestr V

1) Wawawrzyczek Przemysław

2) Zieliński Tomasz

3) Wroński Adam

Przyrządy:

Mikroskop z przesuwanym stolikiem, szklana płytka płasko - równoległa, lampa sodowa.

Światło padając na soczewkę płasko - wypukłą częściowo odbija się od jej wewnętrznej powierzchni, częściowo zaś przenika przez cienką warstwę powietrza i odbija się od płytki szklanej (rys.1). Dzięki tej różnicy dróg tworzą się prążki interferencyjne w kształcie pierścieni (rys.2). Prążki te obserwuje się przez mikroskop ustawiony tak, by jego oś

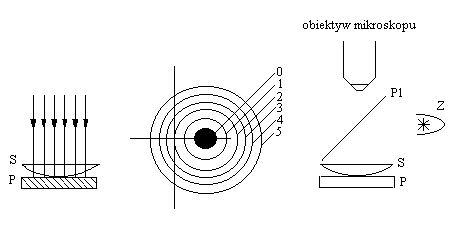
Rys.1. Rys.2. Rys.3

optyczna była równoległa do osi optycznej soczewki. Średnice pierścieni zależne są od promienia R krzywizny soczewki oraz od długości fali światła padającego na soczewkę. Zależność tę opisuje poniższy wzór

(1)

gdzie: d_k - średnica k-tego pierścienia

R - promień krzywizny soczewki

k - kolejny numer pierścienia

Ze wzoru (1) wynika również, że zależność pomiędzy kwadratami średnic kolejnych pierścieni d_k² i ich numerami k, jest zależnością liniową.

Dopasowując zatem do eksperymentalnej zależności d_k²=f(k) prostą regresji liniowej y=ax+b można, na podstawie współczynnika a tej prostej, wyznaczyć długość fali świetlnej. Współczynnik a prostej regresji, jak wynika ze wzoru (1), będzie wówczas określony jako:

(2)

Długość fali λ, po odpowiednim przekształceniu równania (2), wyznacza się ze wzoru:

(3)

gdzie: a - współczynnik prostej regresji,

R - promień krzywizny soczewki.

Przebieg ćwiczenia:

1. Umieścić na stoliku mikroskopu szklana płytkę P wraz z soczewką S (rys.3).

2. Lampę sodową Z ustawić w odległości 0,2 ÷ 0,4 m od mikroskopu.

3. Włączyć lampę sodową.

4. Płytkę szklaną P₁ ustawić pod kątem π/4 rad od osi mikroskopu (patrz rys.3), aby kierowała światło na soczewkę równolegle do jej osi optycznej.

5. Ustawić mikroskop w ten sposób, by widać było ostro górną powierzchnię płytki P.

6. Przesuwając płytkę P wraz z soczewką ustawić ją w takim położeniu, by widać było pierścienie Newtona ułożone centralnie względem środka pola widzenia.

7. Zmierzyć średnicę kilku pierścieni, dla których k>2.W tym celu należy za pomocą śruby przesunąć stolik mikroskopu w takie położenie, by jedna z nici krzyża widocznego w polu obserwacji była styczna do wybranego pierścienia (rys.2). Po odczytaniu położenia a₁ stolika należy przesunąć go w takie położenie, by nitka była styczna do tego samego pierścienia z przeciwnej strony (prostopadła do niej nitka musi stale przebiegać przez środek układu pierścieni). Po odczytaniu położenia a₂ stolika średnicę pierścienia znajdziemy z zależności:

Wyniki pomiarów oraz obliczeń :

Zestawienie pomiarów I :

	a1	a2	Dk [mm]	Dk^2[mm^2]
	4,7	3,5	1,2	1,44
	4,73	3,46	1,27	1,61
	4,76	3,41	1,35	1,82
	4,92	3,52	1,4	1,96
	5,04	3,40	1,64	2,69
	5,08	3,49	1,59	2,52
	5,12	3,5	1,62	2,62
	5,15	3,41	1,74	3,03
	5,18	3,35	1,83	3,35
	5,12	3,39	1,73	2,99
	5,15	3,42	1,73	2,99
	5,18	3,23	1,95	3,80

R= 0,122 +/- 0,01 [m] = 122 +/- 10[mm]

Parametry prostej regresji :

a = 1,91 * 10^-1 = 0,191 [mm²]

b = 7,5473 * 10^-1 = 0,755 [mm²]

Δa = 2,1 * 10^-2 = 0,021 [mm²]

Δb = 2,1 * 10^-1= 0,21 [mm²]

λ= a / 4R = 391 [nm]

Błąd pomiaru

Δλ = ( 0,11 + 0,082) * (391 * 10^-6) = 0,000075 [mm] = 75, 3 [nm]

Wynik końcowy

λ =391 nm ± Δ75nm

Zestawienie pomiarów II :

	a1	a2	Dk [mm]	Dk^2[mm^2]
	0,9	1,53	0,63	0,4
	0,83	1,63	0,8	0,64
	0,76	1,69	0,93	0,86
	0,68	1,77	1,09	1,19
	0,63	1,82	1,19	1,42
	0,59	1,86	1,27	1,61
	0,55	1,91	1,36	1,85
	0,47	1,96	1,49	2,22
	0,38	2	1,62	2,62
	0,3	2,05	1,75	3,06
	0,26	2,08	1,82	3,31
	0,2	2,11	1,91	3,65
	0,15	2,14	1,99	3,96
	0,10	2,18	2,08	4,33
	0,05	2,21	2,16	4,67
	0	2,24	2,24	5,02

R= 0,122 +/- 0,01 [m]

Parametry prostej regresji :

a = 3,1299 * 10^-1 = 0,313 [mm²]

b = -1,1005 * 10^-1 = - 0,110 [mm²]

Δa = 6,5 * 10^-3 =0,0065 [mm²]

Δb = 6,5 * 10^-2 =0,065[mm²]

λ= a / 4R = 641 [nm]

Błąd pomiaru

Δλ = ( 0,0208 + 0,082) * (391 * 10^-6) = 0,0000402 [mm] = 40 [nm]

Wynik końcowy

λ =641 nm ± Δ40nm

Wnioski:

-Przy większej liczbie pomiarów zwiększa się dokładność

-Przy pomiarach przeszkadzały mały rozmiar pierścieni i odległości między nimi oraz światło padającę na mikroskop

---