Politechnika Gdańska Łukasz Majkowski

Wydział Budownictwa Wodnego Grupa B 2

i Inżynierii Środowiska Rok I, semestr II

Katedra Hydrauliki i Hydrologii

POMIAR LEPKOŚCI WISKOZYMETREM HÖPPLERA

CEL I ZAKRES ĆWICZENIA

Opisywane ćwiczenie odbyło się dnia 8 marca 2004 w hali WBWiIŚ. Miało ono na celu wyznaczenie dynamicznego współczynnika lepkości μ w funkcji temperatury dla wybranego płynu.

Wszystkie czynności zawarte w tym doświadczeniu odbywały się w oparciu o czas opadania kulki w glicerynie za pomocą wiskozymetru Höpplera.

WYZNACZENIE WSPÓŁCZYNNIKA LEPKOŚCI

Lepkość - opór przeciw płynięciu gazów i cieczy, wywołany tarciem wewnętrznym. Tarcie stawia opór warstwie płynu, przypływającej wzdłuż powierzchni stałej lub między innymi warstwami płynu.

Lepkość płynu można też określić jako jego zdolność do przenoszenia naprężeń stycznych (naprężeń tarcia wewnętrznego) τ, które dla przypadku przepływu ścinającego związane są z rozkładem prędkości i przedstawia się wzorem:

,

gdzie współczynnik proporcjonalności μ jest miarą lepkości i nazywa się dynamicznym współczynnikiem lepkości i wyraża się jednostką [
].

Siła oporu, która działa na ciało poruszające się w płynie przedstawia się tzw. wzorem Stokesa:

F₀ = 3π∙μ∙u∙d,

ważny dla
, gdzie:

F₀ - siła oporu

μ - dynamiczny współczynnik lepkości

γ - kinematyczny współczynnik lepkości

u - prędkość opadania kulki w cieczy

d - średnica kulki (15,655mm)

Związek między kinematycznym i dynamicznym współczynnikiem lepkości przedstawia się następującą zależnością:

μ = ρ ∙ γ

Lepkość dynamiczna słabo zależy od ciśnienia ale maleje wraz ze wzrostem temperatury.

W warunkach ustalonego opadania kulki II prawo Newtona przyjmuje następującą postać:

F₀ = F_g - F_w

- siła ciężkości

- siła wyporu

ρ - gęstość kulki

ρ_c - gęstość cieczy

g - przyspieszenie ziemskie

Porównując ze sobą wzór Stokesa i równanie II prawa Newtona otrzymujemy zależność:

Na tak przedstawionej zasadzie oparte jest działanie wiskozymetru Höpplera. Powyższy wzór odnosi się do nieograniczonego obszaru cieczy, przez byłyby potrzebne obserwacje opadania kulki w dość dużym naczyniu. W związku z tym w praktyce badaną ciecz umieszcza się w rurce o średnicy niewiele większej od średnicy kulki i obowiązuje poniższy wzór:

μ = 0,102t(γ_k - γ_c) K∙10^-5

0,102 [m] - przelicznik o wymiarze liniowym

t [s] - czas opadania kulki

γ_k
- ciężar właściwy kulki

γ_c
- ciężar właściwy badanej cieczy

K - bezwymiarowa stała kulki

OPIS STANOWISKA BADAWCZEGO - SCHEMAT WISKOZYMETRU HÖPPLERA

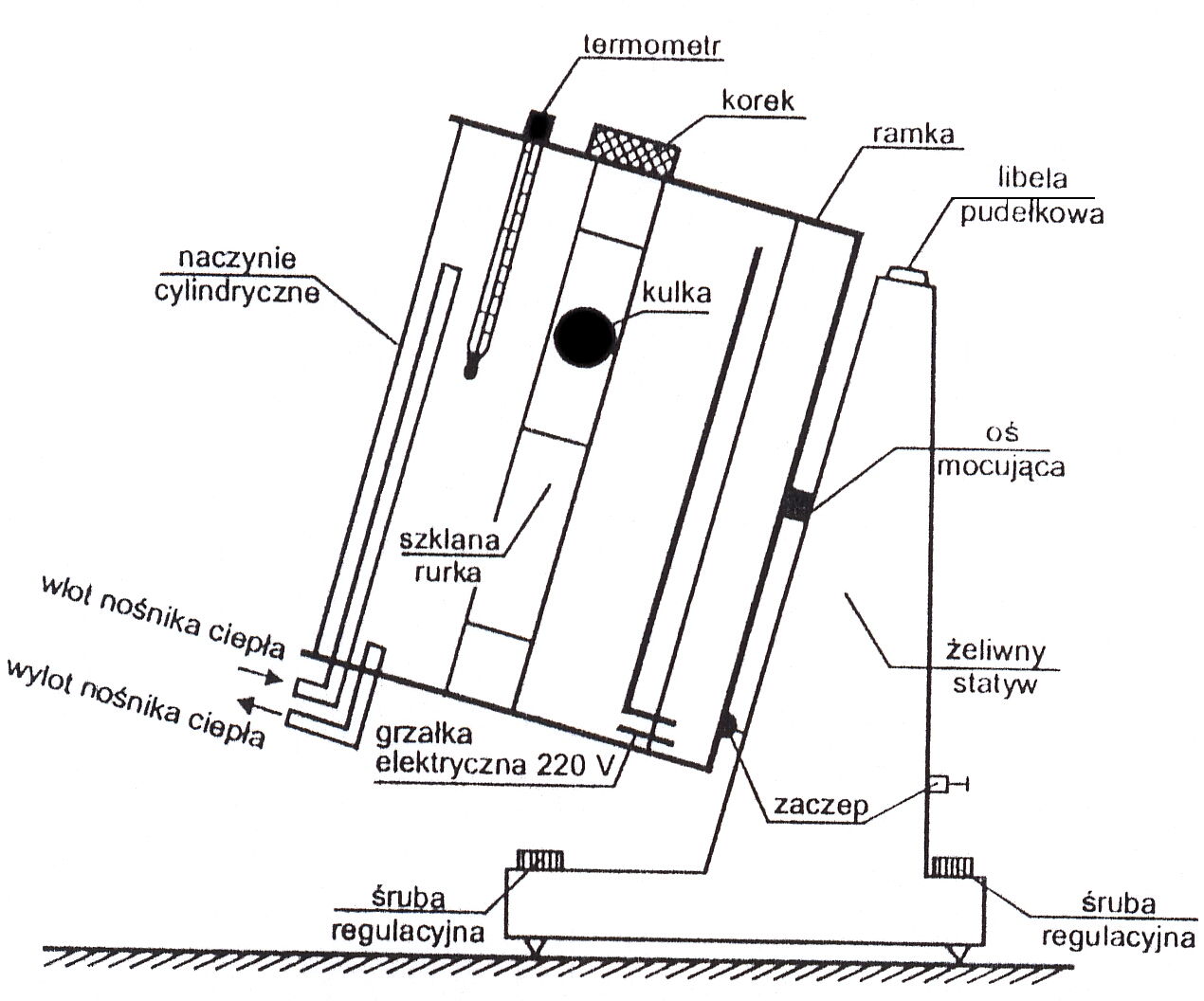
Podczas wykonywania doświadczenia używaliśmy wiskozymetru Höpplera, dwóch stoperów i termostatu. Naczynie cylindryczne, w którym znajduje się szklana rurka wypełniona badaną cieczą nachylone jest pod kątem 10º do pionu. Naczynie to pełni rolę pojemnika umożliwiającego utrzymanie i pomiar stałej temperatury badanej cieczy. Nośnik ciepła dopływał z termostatu. Całość była ujęta w obrotową ramkę, zamocowaną na statywie, który zaopatrzony był w libelę pudełkową. Przed wykonaniem doświadczenia sprawdziliśmy spoziomowanie urządzenia.

PRZEBIEG ĆWICZENIA

1. Zdjąć korek, wypełnić rurkę badaną cieczą (gliceryną), ostrożnie wprowadzić kulkę do rurki i założyć korek. Ważne jest, aby kulka była dobrana w ten sposób, żeby jej czas opadania w rurce wynosił przynajmniej 25 sekund.

2. Ustawić przyrząd na stole, napełnić płaszcz wodny i podłączyć termostat w celu ogrania badanej cieczy do odpowiedniej temperatury. Ponieważ u nas nośnikiem ciepła jest woda destylowana, temperatury pomiarowe mogą być w zakresie od 1ºC do 95ºC.

3. Spoziomować libelę pudełkową.

4. Gdy termometr wskaże żądaną temperaturę, zwolnić zaczep i obrócić cylinder o 180º wokół osi, a gdy kulka opadnie w dół - obrócić naczynie do położenia wyjściowego i zamknąć zatrzask. Podczas opadania kulki dokonać pomiarów czasu stoperami i uśrednić wyniki.

5. Pomiary lepkości gliceryny wykonać dla 22 różnych temperatur T, zaczynając od temperatury bliskiej otoczeniu (tu 16,5ºC), stopniowo zwiększając i kończąc na 62,5ºC.

6. Ze wzoru: μ = 0,102t(γ_k - γ_c) K∙10^-5 obliczyć wartość współczynnika μ dla poszczególnych temperatur T.

7. Otrzymane 22 punkty pomiarowe nanieść na wykres w układzie współrzędnych μ=f(T).

8. W oparciu o uzyskaną konfigurację punktów założyć rodzaj funkcji aproksymującej zależność μ(T) dla gliceryny, wyznaczyć współczynniki najmniejszych kwadratów, narysować wykres otrzymanej funkcji μ(T).

9. Wyznaczyć pozorny błąd względny pomiaru μ metodą różniczki zupełnej:

1. obliczyć pozorny błąd bezwzględny pomiaru temperatury przyjmując, że jest on równy średniemu odchyleniu standardowemu ΔT_p = s

, dla n=22

2. obliczyć |μ'(T)| różniczkując otrzymaną funkcję μ(T) (patrz punkt 8)

3. obliczyć pozorny błąd bezwzględny pomiaru współczynnika μ

Δμ_p = |μ'(T)|ΔT_p

4. na wykres μ(T) nanieść wokół punktów pomiarowych prostokąty, które przedstawiają dokładność pomiarów

OBLICZENIA

Wyniki pomiarów:

Temperatura [ºC]	Czas opadania kulki [min,s,ss]	Czas opadania kulki [s]
16,5	3,42,81	222,81
22	2,33,75	153,75
24	2,12,92	132,92
25,5	2,04,85	124,85
26,5	1,53,39	113,39
27	1,55,40	115,40
29	1,37,39	97,39
29,5	1,29,47	89,47
30	1,34,09	94,09
35,5	1,07,07	67,07
37	1,05,88	65,88
40	0,54,23	54,23
41,5	0,49,31	49,31
43	0,50,53	50,53
45	0,42,45	42,45
46	0,38,17	38,17
48	0,35,73	35,73
51	0,30,74	30,74
53	0,29,58	29,58
55,5	0,25,16	25,16
60	0,21,19	21,19
62,5	0,19,35	19,35

Wszystkie obliczenia wykonujemy przyjmując, że stała kulki K=0,1273, a ciężar właściwy kulki γ_k=79610
.

Dla temperatury 16,5ºC czas opadania kulki wyniósł 222,81s. Z wykresu zależności μ(T) dla gliceryny odczytujemy gęstość gliceryny w danej temperaturze:

ρ_gl=1262,125

Następnie wyliczam ciężar właściwy gliceryny ze wzoru:

γ = ρ_gl ∙ g

gdzie g=9,81
- przyspieszenie ziemskie

γ = 1262,125
∙9,81
=12381,446

Ze wzoru na dynamiczny współczynnik lepkości obliczam ten współczynnik:

μ = 0,102t(γ_k - γ_c) K∙10^-5 = 0,102∙222,81∙(79610-12381,446)∙0,1273∙10^-5=1,944988439

W powyższy sposób policzyłem współczynniki lepkości dla pozostałych temperatur i zestawiłem je w tabeli.

Kolejne dane można wyliczyć, jeśli będzie znany wzór funkcji μ(T). Najwygodniejszym i chyba najłatwiejszym sposobem jest metoda najmniejszych kwadratów (MNK), która sprowadza się do warunku, aby suma S kwadratów odchyleń mierzonych wartości y_i od wartości obliczonych f(x_i,a₀,...,a_n) przyjmowała wartość najmniejszą. W ten sposób wyznaczę postać szukanego równania, zależność między zmiennymi i liczbą stałych.

Dla ogólnego przypadku (pomiary funkcji y₁,y₂,...,y_n przeprowadzono z jednakową dokładnością) warunek brzmi:

minimum

Zagadnienie określenia tych wartości parametrów a₀,a₁,a₂,...,a_n, dla których funkcja S=S(a₀,a₁,a₂,...,a_n) przyjmuje najmniejszą wartość, sprowadza się do rozwiązania układu równań:

Rozwiązanie tego układu jest szczególnie proste, gdy funkcja f(x_i,a₀,...,a_n) jest liniowa względem parametrów a_i. Gdy jest nieliniowa, to dla funkcji typu wykładniczego:

y = b ∙ a^x

logy = logb ∙ x ∙ loga

Y = logy

B = logb

A = loga

Y = Ax + B

W związku z powyższym można teraz ograniczyć się do rozważania funkcji liniowych, dla których omawiana metoda prowadzi do zależności:

minimum

Funkcja S=S(a,b) osiąga minimum, gdy jej pochodne cząstkowe względem a i b są równe zero:

Dla naszej funkcji układ przyjmuje postać:

Stąd rozwiązanie tego układu ma postać:

A=loga B=logb

a=0,95 b=4,04

W związku z powyższym wzór szukanej funkcji będzie miał następującą postać:

y = 4,04 ∙ (0,95)^x → μ(T) = 4,04 ∙ (0,95)^T

Następnie obliczam pozorny błąd bezwzględny metodą różniczki zupełnej.

Najpierw liczę pozorny błąd bezwzględny pomiaru temperatury:

, dla n=22

s=0,25ºC

Następnie obliczam μ'(T):

dla 16,5ºC: μ'(T)=4,04 ∙ (0,95)^16,5 ∙ ln(0,95)= - 0,0884

Teraz obliczam pozorny błąd bezwzględny pomiaru współczynnika μ ze wzoru:

Δμ_p = |μ'(T)|ΔT_p, gdzie ΔT_p=s

dla 16,5ºC: Δμ_p = 0,0884 ∙ 0,25=0,0221

Pozostałe wyniki znajdują się w poniższej tabeli.

Otrzymane punkty (błędy) bezwzględne należy nanieść na wykres μ(T) wokół punktów pomiarowych w postaci prostokątów charakteryzujących dokładność pomiarów.

WYNIKI POMIARÓW DLA GLICERYNY:

i	Ti [ºC]	γ	μ	s [ºC]	μ'(T)	Δμ
1	16,5	12381,446	1,944988439	0,25	-0,088421	0,022135788
2	22	12354,223	1,342682394	0,25	-0,066884	0,016720997
3	24	12345,885	1,160920127	0,25	-0,060214	0,015053553
4	25,5	12341,715	1,090504539	0,25	-0,055652	0,013913028
5	26,5	12333,377	0,990529728	0,25	-0,052804	0,013201099
6	27	12329,208	1,008150754	0,25	-0,051436	0,012858914
7	29	12325,038	0,850865574	0,25	-0,046306	0,011576603
8	29,5	12320,869	0,781719476	0,25	-0,045106	0,011276527
9	30	12316,7	0,830874153	0,25	-0,043937	0,010984229
10	35,5	12289,6	0,586277962	0,25	-0,032913	0,007604813
11	37	12279,177	0,575964994	0,25	-0,030419	0,006496117
12	40	12262,5	0,474230693	0,25	-0,025984	0,006003942
13	41,5	12256,124	0,431247084	0,25	-0,024016	0,005549056
14	43	12243,615	0,441998827	0,25	-0,022196	0,004995696
15	45	12241,531	0,371332488	0,25	-0,019983	0,004740066
16	46	12226,939	0,333965397	0,25	-0,01896	0,004267379
17	48	12220,68	0,312645848	0,25	-0,011707	0,003645244
18	51	12199,839	0,269065368	0,25	-0,014581	0,003281734
19	53	12189,416	0,258951991	0,25	-0,013127	0,002877892
20	55,5	12172,739	0,220312498	0,25	-0,011512	0,002272074
21	60	12145,516	0,18562426	0,25	-0,009088	0,001992478
22	62,5	12124,669	0,169558251	0,25	-0,00797	0,001991265

CIECZ STUDENTA

Dla cieczy studenta wykonuję takie same obliczenia jak do tej pory, z tą tylko różnicą, że ciężar właściwy mnożę przez współczynnik 1,66
.

Dla temperatury 16,5ºC:

μ = 0,102t(γ_k - γ_c∙1,66) K∙10^-5 = 0,102∙222,81∙(79610-20553,2)∙0,1273∙10^-5=1,708857

Szukam wzoru funkcji:

y = b ∙ a^x

logy = logb ∙ x ∙ loga

Y = logy

B = logb

A = loga

Y = Ax + B

A=loga B=logb

a=0,88 b=1,49

W związku z powyższym wzór szukanej funkcji będzie miał następującą postać:

y = 1,49 ∙ (0,88)^x → μ(T) = 1,49 ∙ (0,88)^T

Następnie obliczam pozorny błąd bezwzględny metodą różniczki zupełnej.

Najpierw liczę pozorny błąd bezwzględny pomiaru temperatury:

, dla n=22

s=0,25ºC

Następnie obliczam μ'(T):

dla 16,5ºC: μ'(T)=1,49 ∙ (0,88)^16,5 ∙ ln(0,88)= - 0,0884

Teraz obliczam pozorny błąd bezwzględny pomiaru współczynnika μ ze wzoru:

Δμ_p = |μ'(T)|ΔT_p, gdzie ΔT_p=s

dla 16,5ºC: Δμ_p = 0,0884 ∙ 0,25=0,0221

Pozostałe wyniki znajdują się w poniższej tabeli.

Otrzymane punkty (błędy) bezwzględne należy nanieść na wykres μ(T) wokół punktów pomiarowych w postaci prostokątów charakteryzujących dokładność pomiarów.

WYNIKI DLA CIECZY STUDENTA:

Wsp. studenta	i	Ti [ºC]	γ	μ	s [ºC]	μ'(T)	Δμ
1,66	1	16,5	20553,2	1,708857	0,25	-0,02345	0,0058625
1,66	2	22	20508,01	1,179901	0,25	-0,01141	0,0028525
1,66	3	24	20494,16	1,020287	0,25	-0,00883	0,0022075
1,66	4	25,5	20487,25	0,958455	0,25	-0,00729	0,0018225
1,66	5	26,5	20473,4	0,870682	0,25	-0,00642	0,001605
1,66	6	27	20466,48	0,886220	0,25	-0,00602	0,001505
1,66	7	29	20459,56	0,747998	0,25	-0,00466	0,001165
1,66	8	29,5	20452,64	0,687250	0,25	-0,00437	0,0010925
1,66	9	30	20445,72	0,722822	0,25	-0,00410	0,001025
1,66	10	35,5	20400,73	0,515639	0,25	-0,00203	0,0005075
1,66	11	37	20383,43	0,506639	0,25	-0,00167	0,0004175
1,66	12	40	20355,75	0,417241	0,25	-0,00114	0,000285
1,66	13	41,5	20345,16	0,379455	0,25	-0,00093	0,0002325
1,66	14	43	20324,4	0,388979	0,25	-0,00087	0,0002175
1,66	15	45	20320,94	0,326799	0,25	-0,00083	0,0002075
1,66	16	46	20296,71	0,293969	0,25	-0,00080	0,0002
1,66	17	48	20286,32	0,275226	0,25	-0,00076	0,00019
1,66	18	51	20251,73	0,236926	0,25	-0,00072	0,00018
1,66	19	53	20234,43	0,228052	0,25	-0,00065	0,0001625
1,66	20	55,5	20206,75	0,194065	0,25	-0,00058	0,000145
1,66	21	60	20161,55	0,163568	0,25	-0,00049	0,0001225
1,66	22	62,5	20126,95	0,149452	0,25	-0,00044	0,00011

---