1. Obliczam wartość promienia wewnętrznego rury wiskozymetru R.
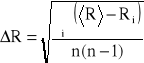
<R>=Σ(d / 2) / 5=3,075 cm
Szacuję niepewność pomiarową ΔR.
Stąd
R=2,8075 cm
ΔR=0 cm
2. Wyznaczam niepewność pomiarową Δm i masy kulek m1, m2, m3.
m1= 0,2196 g
Niepewność pomiarowa związana z dokładnością wagi przyjmuję jako 0,1 mg .
Całkowita niepewność pomiarowa będzie sumą niepewności przyrządu i niepewności przypadkowej.
Δmp=0,1 mg , Δms=0,05 mg
wtedy Δm1= Δmp + Δms=0,15 mg czyli
Δm1=0,00015 g
3. Obliczam wartość średnią promienia kulki <r> oraz Δr.
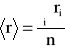
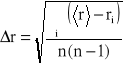
Obliczenia dla kulki nr 1
<r>= 0,2969 cm
Δr= 0,016539 cm
Obliczenia dla kulki nr 2
<r>=0,2855 cm
Δr= 0,01546932 cm
Obliczenia dla kulki nr 3
<r>= 0,2791 cm
Δr= 0,01217128 cm
Δr/r=8,6 %
4. Obliczam wartość średnią prędkości opadania kulki Vk oraz Δ Vk.
<Vk> = ΔS / Δt w [cm / s]
Δ Vk=(ΔS/S - Δt/t) <Vk>
ΔS=0,1 cm
Δt=0,01 s
Obliczenia dla kulki nr 1,2,3.
Droga Δs |
10 cm |
20 cm |
30 cm |
40 cm |
50 cm |
Wartości średnie |
V kulki 1 |
8.5763 |
4.2808 |
2.7502 |
1.9135 |
1.4302 |
12.42 |
V kulki 2 |
17.5131 |
9.7087 |
5.7471 |
4.3591 |
3.1786 |
12.44 |
Prędkości w powyższej tabeli podane są w [cm / s]
Jak widać wyniki wykazują tendencję do spadku wartości, co może być spowodowane tym, że odczyt kolejnych czasów odbywał się na różnych wysokościach wiskozymetru Stokesa i co za tym idzie zmieniał się kąt patrzenia na kulkę względem znaczników na wiskozymetrze.
Obliczam Δ Vk=(ΔS/S - Δt/t) <Vk>
Droga ΔS |
10 cm |
20 cm |
30 cm |
40 cm |
50 cm |
ΔV kulki 1 |
0.0015 |
0.0006 |
0.0003 |
0.0002 |
0.0001 |
ΔV kulki 2 |
0.0024 |
0.0009 |
0.0004 |
0.0003 |
0.0002 |
Wartości w powyższej tabeli podane są w [cm / s]
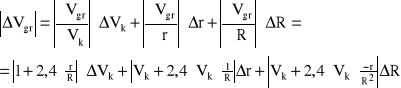
5. Obliczam wartość prędkości granicznej (dla naczynia o nieskończonych rozmiarach) korzystając z wzoru Landenburga Vgr=Vk {1 + 2,4 ⋅ (r / R)}
Stąd : dla kulki nr 1
Vgr=6.4054 [cm / s]
ΔVgr =0,42 [cm / s]
dla kulki nr 2
Vgr = 6.3226 [cm / s]
ΔVgr =0,65 [cm / s]
![]()
6. Obliczam wartość współczynnika lepkości cieczy η korzystając ze wzoru
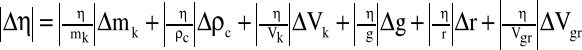
gdzie Vk=4/3 πr3 - objętość kulki.
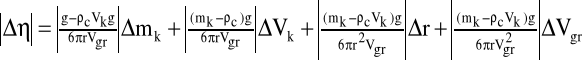
Wartości ρc oraz g zostały wzięte z tablic, zakładam więc, że są one bardzo dokładne, co oznacza ,że przy obliczaniu wartości błędu można je pominąć.
η1=0,306 [g / (s cm)]
η2=0,392 [g / (s cm)]
η3=0,332 [g / (s cm)]
ηśr=0,343 [g / (s cm)]
Po podstawieniu do wzoru :
Δη1=0,13 [g / (s cm)]
Δη2=0,26 [g / (s cm)]
Δη3=0,12[g / (s cm)]
Δηśr=0,17 [g / (s cm)]
Co daje ostatecznie
η1=0,306 ± 0,13 [g / (s cm)]
η2=0,392 ± 0,26 [g / (s cm)]
η3=0,332 ± 0,12 [g / (s cm)]
oraz
ηśr=0,343 ± 0,17 [g / (s cm)]
W porównaniu z wartością tablicową η=4,94 [g /(cm s)] otrzymany wynik nie jest zbyt podobny . Sądzę, że doszło tu do skumulowania się kilku czynników: między innymi niepewności obserwatora jak i niedoskonałości sprzętu.
Wyznaczanie lepkości cieczy metodą Stokesa
Opracowanie wyników
7
![]()
![]()
![]()
![]()
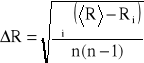
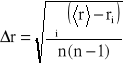
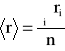
Wyszukiwarka
Podobne podstrony:
Pomiar lepkośći cst, FIZYKA9A, ggggg
Pomiar lepkośći cst, FIZ 1, ˙I˙ PRACOWNIA FIZYCZNA U.˙.
Pomiar lepkośći cst, FIZ 1 1, ˙I˙ PRACOWNIA FIZYCZNA U.˙.
Pomiar lepkośći cst, Lepkość cieczy, Politechnika Śląska
Pomiar lepkośći cst, FIZYK20C, ˙I" PRACOWNIA FIZYCZNA U
Obliczyć wartości głównych ?ntralnych osi?zwładności przekroju
Pomiar lepkości olejów
Obliczanie wartosci wielomianów schemat Hornera
Przyblizone obliczanie wartosci pochodnej metoda numeryczna
Pomiar lepkości1
Pomiar lepkości2
Ćw nr 4, cw36, POMIAR LEPKOŚCI CIECZY 36
Obliczanie wartości obciążenia granicznego układu belkowo słupowego
91 Obliczenie funkcji sił wewnętrznych
Pierwsze strony Pomiar lepkości
Oznaczanie ciepła spalania i obliczanie wartości opałowej
Pomiar lepkości
więcej podobnych podstron