4. Podstawy podejmowania decyzji i inżynierii wiedzy

1. Architektura systemu ekspertowego: definicje systemu ekspertowego, metody reprezentacji wiedzy, metody pozyskiwania wiedzy, metody wnioskowania w systemach ekspertowych, elementy badania poprawności bazy wiedzy.

System ekspertowy to:

• program komputerowy posiadający wiadomości w formie bazy wiedzy i przeprowadzający wnioskowanie z możliwością rozwiązywania problemów i doradztwa.

• program komputerowy, który prezentuje sobą, w pewnej ściśle określonej dziedzinie, stopień doświadczenia w rozwiązywaniu problemów porównywalny ze stopniem doświadczenia i wiedzy eksperta

Cechą charakterystyczną systemu eksperckiego jest wyróżnienie reprezentacji wiedzy o dziedzinie, której dotyczy system oraz mechanizmu rozumowania na podstawie zasobów wiedzy z tej dziedziny. System ekspercki w swej strukturze zawiera takie elementy, które umożliwiają jego działanie w sposób porównywalny z najlepszymi specjalistami tzn. ma zdolność:

• Zadawania pytań w celu uzyskania odpowiednich informacji od użytkownika

• Wyjaśniania sposobu rozumowania na żądanie użytkownika

• Uzasadniania otrzymanych konkluzji

• Modyfikowania sposobu działań

W systemie eksperckim wyróżnia się następujące elementy główne :

1. elementy programu wykonywane podczas współdziałania użytkownika z systemem eksperckim

• procedury sterowania dialogiem pomiędzy użytkownikiem systemu a systemem eksperckim

• procedury wnioskowania

• procedury objaśniania

• procedury aktualizacji bazy wiedzy

2. elementy nie wykonywane stanowiące odpowiednie bazy a więc

• baza wiedzy

• baza danych stałych

• baza danych zmiennych

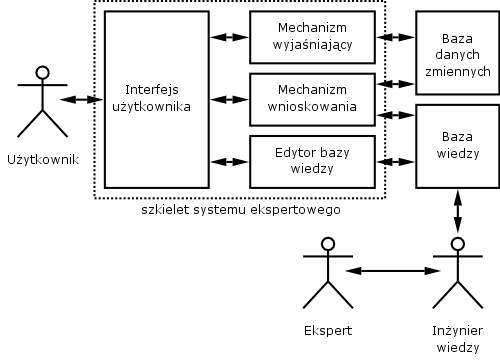
W skład systemu eksperckiego wchodzą:

• baza wiedzy - zawiera reprezentację wiedzy z danej dziedziny niezbędnej w procesie rozwiązywania problemów decyzyjnym. Reprezentacja wiedzy w bazie wiedzy może mieć charakter deklaratywny (reguły, fakty) lub proceduralny (procedury, funkcje)

• moduł wnioskowania - zadaniem moduły jest przeszukiwanie elementów bazy wiedzy, ustalenie kolejności ich analizowania i sprawdzenie warunków ich stosowalności

• baza danych stałych i baza danych zmiennych - stanowią zbiory danych (stwierdzeń) zorganizowanych według ustalonego sposobu. Baza danych zmiennych zawiera odpowiedzi użytkownika oraz wnioski pośrednie wyznaczone przez układ wnioskowania a także wykaz działań zawieszonych ze względu na brak określonych stwierdzeń w bazie

• interfejs użytkownika - umożliwia prowadzenie dialogu użytkownika z systemem. Interfejs użytkownika jest często dzielony na interfejs wejściowy i wyjściowy

• moduł pozyskiwania wiedzy - umożliwia pozyskiwanie i gromadzenie wiedzy w celu zwiększenia efektywności systemu

• moduł objaśniania - uzasadnia decyzje podejmowane przez moduł wnioskowania systemu eksperckiego poprzez przedstawienie toku rozumowania

METODY POZYSKIWANIA WIEDZY:

• bezpośrednie zapisywanie wiedzy tzn. uczenie na pamięć. Metoda ta nie wymaga żadnego działania typu wnioskowanie lub transformowanie wiedzy od uczącego się systemu

• pozyskiwanie wiedzy na podstawie instrukcji. Metoda ta wymaga udziału nauczyciela w procesie pozyskiwania wiedzy i polega na wykorzystaniu źródeł wiedzy wskazanych przez nauczyciela oraz przekształceniu wiedzy do postaci akceptowalnej przez system

• pozyskiwanie wiedzy na podstawie analogii. Metoda ta polega na przekształceniu istniejącej wiedzy w bazie wiedzy w celu umożliwienie opisu faktów podobnych do faktu opisanego uprzednio

• pozyskiwanie wiedzy na podstawie przykładów. Jest to szczególny przypadek uczenia indukcyjnego. Polega na generowaniu ogólnego opisu pojęć na podstawie zbioru przykładów oraz kontrprzykładów obiektów reprezentujących te pojęcia. Przykłady mogą być określone przez eksperta na podstawie wcześniej utworzonych baz danych

• pozyskiwanie wiedzy na podstawie odkrywania i obserwacji. Metoda ta jest często nazywana uczeniem bez nauczyciela i stanowi ogólny przypadek uczenia indukcyjnego który wymaga zwiększonego udziału uczącego w procesie uczenia.

METODY REPREZENTACJI WIEDZY - to metody zapisania pozyskanej wiedzy w maszynach cyfrowych, w sposób najbliższy sposobowi rozumowania człowieka. P

powinna umożliwiać prosty, kompletny (wyczerpujący), zwięzły, zrozumiały i wyraźny zapis wiedzy.

• metody bazujące na bezpośrednim zastosowaniu logiki takie jak: rachunek zadań, rachunek predykatów

• metody wykorzystujące zapis stwierdzeń

• metody bazujące na sieciach semantycznych

• metody wykorzystujące systemy regułowe i zapis reguł

• ramy

• tabele decyzyjne

• drzewa decyzyjne

• metody przybliżonej reprezentacji wiedzy.

Podział reprezentacji wiedzy ze względu na techniki zapisu wiedzy :

• reprezentacja proceduralna - polega na określeniu zbioru procedur których działanie reprezentuje wiedzę o dziedzinie

• reprezentacja deklaratywna - zbiór specyficznych dla danej dziedziny faktów stwierdzeń i reguł(wykłady Piłota)

Wnioskowanie - proces, w którym na podstawie zadań uznanych za prawdziwe dochodzi się do nowego zdanie dotąd nieuznanego (konkluzji).

METODY WNIOSKOWANIA

1. wnioskowanie logiczne

• dedukcja

• abdukcja

• indukcja

• wnioskowanie na bazie niespójności

• wnioskowanie nie monotoniczne

2. wnioskowanie pochodne od logiki

• wstecz

• wprzód

• mieszane

3. algorytmy dopasowania wzorca

4. metody szukania

5. wnioskowanie przez analogię

6. metody uczenia parametrycznego i strukturalnego

Ze względu na metodę prowadzenia procesu wnioskowania systemy ekspertowe dzieli się na:

• z logiką dwuwartościową (Boole'a),

• z logiką wielowartościową,

• zlogiką rozmytą.

 Ze względu na rodzaj przetwarzanej informacji systemy ekspertowe dzielą się na dwie grupy:

• systemy z wiedzą pewną, czyli zdeterminowaną,

• systemy z wiedzą niepewną, w przetwarzaniu, której wykorzystuje się przede wszystkim aparat probabilistyczny.

BADANIA POPRAWNOŚCI BAZY WIEDZY

Spójność - wykrywanie reguł zbędnych, sprzecznych, pochłaniających, ze sprzecznym warunkiem oraz zapętlonych, kompletność bazy reguł - poszukiwanie reguł brakujących.

Spójność reguł:

Sprzeczność: dwie reguły są sprzeczne, jeśli ich części warunkowe są równocześnie spełnione lub nie spełnione we wszystkich możliwych przypadkach oraz ich konkluzje są różne. Przykład: (a,L) ^ (c, 3)=>(d,H), (a,L) ^ (c, 3) =>(d,L)

Reguły pochłaniające - jedna reguła jest pochłaniana wówczas, gdy część warunkowa pierwszej reguły jest spełniona, jeśli jest spełniona część warunkowa drugiej reguły i konkluzje obu reguł są identyczne. Przykład: (a,L) ^ (c, 3)=>(d,H), (c,3)=>(d,H)

Niepotrzebne warunki: dwie reguły mają niepotrzebne warynki, jeśli obie są pochłaniane przez trzecią regułę. Przykład: (a,L)^(b,D)^(c,5)=>(d,H), (a,R)^(b,D)^(c,5)=>(d,H).

Zapętlenie reguł: Zestaw reguł tworzy pętlę jeśli zapętlenie tych reguł jest cykliczne. Przykład: (a,L)^(c,5)=>(d,H), (d,H)=>(f,2), (f,2)^(g,4)=>(c,5)

Wielokrotne odwoływanie do jednego atrybutu: Występuje wtedy, gdy w części warunkowej są człony zawierające ten sam atrybut. Przykład: (a,L)^(a,R)=>(d,H)

1. Teoria zbiorów rozmytych - definicje zbioru, liczby i przykłady operacji, przykład wnioskowania rozmytego.

Teoria zbiorów rozmytych jest uogólnieniem klasycznej teorii zbiorów. Teoria klasyczna mówi ze element należy bądź nie należy do zbioru. Czyli funkcja przynależności według klasycznej teorii zbiorów może przyjmować tylko wartość 0 lub 1. W teorii zbiorów rozmytych element może częściowo należeć do jakiegoś zbioru a przynależność tę można wyrazić z pomocą liczby rzeczywistej z zakresu 0 do 1Tojęcie ZBIORÓW ROZMYTYCH jako uogólnienie zbiorów zwykłych (nie rozmytych) zostało wprowadzone przez L. Zadehaw w 1965r. Tradycyjny sposób reprezentowania elementu x zbioru A odbywa się za pośrednictwem funkcji charakterystycznej μ(x) równej jeden, gdy element należy do zbioru A lub zero gdy element nie należy do tego zbioru. W systemach rozmytych element może należeć do każdego zbioru częściowo. Stopień przynależności do zbioru A stanowiący uogólnienie funkcji charakterystycznej jest zwany funkcją przynależności μ(x), przy czym μ(x) ∈ [0, 1]

Operacje na liczbach rozmytych

Wprowadźmy definicję liczby rozmytej (Zadeh 1965).

Definicja. Liczbą rozmytą A nazywamy zbiór rozmyty określony na zbiorze liczb rzeczywistych R co zapisujemy:

A ⊆ R., μ: R → [0,1]

Podstawowe operacje na liczbach rozmytych można zdefiniować stosując zasadę rozszerzania (Zadeh 1965):

Definicja. Niech dana będzie pewna operacja dwuargumentowa na

liczbach rzeczywistych:

* : R x R → R

Ponadto, niech A i B będą liczbami rozmytymi A, B ⊆ R, wtedy operację `*' można rozszerzyć na argumenty rozmyte A i B w następujący sposób:

μ(z) = min {μ(x), μ(y)}

OPERACJE NA ZBIORACH ROZMYTYCH

• Suma logiczna A ∪ B

μ(x) = μ(x) ∪ μ(y) = Max [A(x), B(x)]

gdzie znak ∪ oznacza operator Max

przykład:

A= {, , , }

B= {, , , }

C = A ∪ B

C = {, , , }

• Iloczyn logiczny zbiorów A ∩B

μ∩ (x) = μ(x) ∩ μ(x) = Min [A(x), B(x)]

przy czym symbol ∩ oznacza operator Min

C = A ∩B

C = {, , , }

• Negacja zbioru A

μ(x) = 1 - μ(x)

w odróżnieniu od zbiorów zwykłych gdzie negacja elementów należących do zbioru tworzyła zbiór pusty, negacja w odniesieniu do zbiorów rozmytych definiuje zbiór niepusty o elementach z funkcjami przynależności należącymi również do przedziału

[0, 1]

• Równość zbioru A i B

Zbiory rozmyte A(x) i B(x) są sobie równe, gdy dla wszystkich elementów xi obu zbiorów zachodzi μ(xi) = μ(xi)

• Operacja koncentracji CON(A)

μ(x) = [μ(x)]²

jest to szczególnie często używana operacja w działaniach na zmiennej lingwistycznej gdzie utożsamia się ja z intensyfikatorem „bardzo”

• Operacja rozciągania DIL(A)

μ(x) = [μ(x)]

operacja ta w znaczeniu lingwistycznym oznacza „mniej więcej”

• Iloczyn algebraiczny A*B

μ(x) = μ(x) * μ(x)

• Suma ograniczona dwu zbiorów rozmytych A|+|B

μ(x) = min {1, μ(x) + μ(x)}

• Różnica ograniczona dwu zbiorów rozmytych A|-|B

μ(x) = max {0, μ(x) - μ(x)}

• Iloczyn ograniczony dwu zbiorów rozmytych A|*|B

μ(x) = max {0, μ(x) + μ(x) - 1}

• Normalizacja zbioru NORM(A)

μ(x) =

Zbiór A zawiera się w zbiorze B to jest A⊂B jeśli dla wszystkich elementów zachodzi nierówność:

μ(xi) ≤ μ(xi)

Zbiory rozmyte (ang. fuzzy sets) są wykorzystywane do formalnego określania nieostrych, nieprecyzyjnych lub wieloznacznych pojęć, np. "wysokie drzewo", "piękny krajobraz", itd. Mają one swoje źródło w rozwoju teorii sterowania, teorii systemów i zw. logik wielowartościowych. Zauważono, bowiem, że chociaż umysł ludzki jest zdolny do rozumowania w kategoriach przybliżonych, to mimo to jest w stanie przetwarzać dane przybliżone i niejednoznaczne oraz wyznaczać przybliżone rozwiązania, czego nie są w stanie zrobić komputery działające w oparciu o ścisłe reguły. W teorii zbiorów rozmytych funkcja charakterystyczna została uogólniona i nazywa się funkcją przynależności. Przyporządkowuje ona każdemu elementowi zbioru wartości z przedziału [0,1], zamiast tylko jedną z wartości z dwuelementowego zbioru {0,1}, jak to jest w klasycznej teorii zbiory.

Logiczną podstawą pojęcia podzbioru rozmytego jest logika wielowartościowa. Podzbiór rozmyty umożliwia opisanie pojęć, których granica między posiadaniem pewnej własności i jej brakiem jest rozmyta.

2. Zadania realizowane przez sieci neuronowe - architektura przykładowych sieci i metody uczenia.

SIEĆ NEURONOWA - jest równoległym systemem wieloprocesorowym, zorganizowanym na wzór struktur przetwarzania w biologicznej sieci neuronowej (w mózgu człowieka). Podstawowym elementem tej sieci jest prosty procesor dokonujący dwuwartościowej selekcji sumarycznego pobudzenia wejść i wytwarzający jedno z alternatywnych wyjść odpowiadających pobudzeniu podprogowemu i ponad progowemu. Wielkość pobudzenia jest funkcją wag poszczególnych wejść, w procesie uczenia wartości wag są modyfikowane. Procesor realizujący taką funkcję jest nazywany neuronem, przez analogię do sieci biologicznej.

ZADANIA REALIZOWANE PRZEZ SIECI NEURONOWE

• Rozpoznawanie wzorców (znaków, liter, kształtów, sygnałów mowy, sygnałów sonarowych) Klasyfikowanie obiektów

• Prognozowanie i ocena ryzyka ekonomicznego

• Prognozowanie zmian cen rynkowych (giełdy, waluty)

• Ocena zdolności kredytowej

• Ocena wniosków ubezpieczeniowych

• Rozpoznawanie wzorów podpisów

• Prognozowanie zapotrzebowania na energię elektryczną

• Diagnostyka medyczna

• Dobór pracowników

• Prognozowanie sprzedaży

• Analizowanie zachowań klienta w supermarketach

• Aproksymowanie wartości funkcji

METODY UCZENIA SIECI

1. Uczenie pod NADZOREM

Przy tym uczeniu każdemu wektorowi wejściowemu towarzyszy zadany wektor wyjściowy. Dane uczące są podane w postaci par uczących.

Celem uczenia pod nadzorem minimalizacja odpowiednio zdefiniowanej funkcji celu, która w wyniku umożliwi dopasowanie wartości aktualnych odpowiedzi neuronów wyjściowych do wartości żądanych dla wszystkich par uczących.

2. Uczenie z KRYTYKIEM

Uczenie z krytykiem jest odmianą uczenia pod nadzorem, w którym nie występuje informacja o wartościach żądanych na wejściu systemu a jedynie informacja czy podjęta przez system akcja daje wyniki pozytywne w sensie pożądanego zachowania systemu czy negatywne.

3. Uczenie samoorganizujące się typu HEBBA

W modelu Hebba wykorzystuje się wynik obserwacji neurobiologicznych zgodnie, z którymi waga powiązań między dwoma neuronami wzrasta przy jednoczesnym stanie pobudzenia obu neuronów w przeciwnym wypadku maleje.

4. Uczenie samoorganizujące się typu KONKURENCYJNEGO

W uczeniu typu konkurencyjnego neurony współzawodniczą ze sobą, aby stać się aktywnymi (pobudzonymi). W odróżnieniu do uczenia Hebba gdzie dowolna liczba neuronów może być aktywna w uczeniu konkurencyjnym tylko jeden z neuronów może być aktywny a pozostałe pozostają w stanie spoczynku z tego powodu uczenie to nosi tez nazwę WTA (Winner Takes All). Uczenie typu WTA nie wymaga nauczyciela i odbywa się zwykle z zastosowaniem znormalizowanych wektorów wyjściowych

Uczenie metodą wstecznej propagacji błędów:

Pierwszą czynnością w procesie uczenia jest przygotowanie dwóch ciągów danych: uczącego i weryfikującego. Ciąg uczący jest to zbiór takich danych, które w miarę dokładnie charakteryzują dany problem. Jednorazowa porcja danych nazywana jest wektorem uczącym. W jego skład wchodzi wektor wejściowy, czyli te dane wejściowe, które podawane są na wejścia sieci i wektor wyjściowy, czyli takie dane oczekiwane, jakie sieć powinna wygenerować na swoich wyjściach. Po przetworzeniu wektora wejściowego, nauczyciel porównuje wartości otrzymane z wartościami oczekiwanymi i informuje sieć czy odpowiedź jest poprawna, a jeżeli nie, to, jaki powstał błąd odpowiedzi. Błąd ten jest następnie propagowany do sieci, ale w odwrotnej niż wektor wejściowy kolejności (od warstwy wyjściowej do wejściowej) i na jego podstawie następuje taka korekcja wag w każdym neuronie, aby ponowne przetworzenie tego samego wektora wejściowego spowodowało zmniejszenie błędu odpowiedzi. Procedurę taką powtarza się do momentu wygenerowania przez sieć błędu mniejszego niż założony. Wtedy na wejście sieci podaje się kolejny wektor wejściowy i powtarza te czynności. Po przetworzeniu całego ciągu uczącego (proces ten nazywany jest epoką) oblicza się błąd dla epoki i cały cykl powtarzany jest do momentu, aż błąd ten spadnie poniżej dopuszczalnego. Jak to już było zasygnalizowane wcześniej, SSN wykazują tolerancję na nieciągłości, przypadkowe zaburzenia lub wręcz niewielkie braki w zbiorze uczącym. Jest to wynikiem właśnie zdolności do uogólniania wiedzy.

Algorytm uczenia Kohonena:

Sieć Kohonena posiada tylko dwie warstwy: warstwę wejściową oraz warstwę wyjściową, składającą się z neuronów radialnych. Warstwa ta znana jest również jako warstwa tworząca mapę topologiczną, ponieważ takie jest jej najczęstsze zastosowanie. Neurony w warstwie tworzącej mapę topologiczną są rozważane w taki sposób, jakby były rozmieszczone w przestrzeni według jakiegoś ustalonego wzoru.

Sieci Kohonena uczone są przy wykorzystaniu algorytmu iteracyjnego. Rozpoczynając od początkowych, wybranych w sposób losowy centrów radialnych, algorytm stopniowo modyfikuje je w taki sposób, aby odzwierciedlić skupienia występujące w danych uczących.

Siec Hopfielda:

Strukturę sieci Hopfielda można opisać bardzo prosto - jest to układ wielu identycznych elementów połączonych metodą każdy z każdym. Jest, zatem najczęściej rozpatrywana jako struktura jednowarstwowa. W odróżnieniu od sieci warstwowych typu perceptron sieć Hopfielda jest siecią rekurencyjną, gdzie neurony są wielokrotnie pobudzane w jednym cyklu rozpoznawania, co uzyskuje się poprzez pętle sprzężenia zwrotnego.

Wagi połączeń wyliczane są w sieci Hopfielda a priori, jej faza uczenia ogranicza się do wyliczenia wartości wag zgodnie zasadą uczenia Hebba.

ZASTOSOWANIE SIECI NEURONOWYCH

Sztuczne sieci neuronowe mają zastosowanie w działaniach wymagających kojarzenia, rozpoznawania i przewidywania na podstawie poznanych wcześniej danych. SSN znajdują zastosowanie również tam, gdzie ze względu na złożoność opisywanego procesu czy obiektu trudno jest sformułować klasyczny model.

Sztuczne sieci neuronowe stosowane są w wielu problemach, głownie takich, gdzie nie sprawdzają się metody tradycyjne i analityczne. Problemy te można sklasyfikować w kilku grupach, nie zawsze rozłącznych:

- aproksymacja

- autoasocjacja

- klasyfikacja

- podobieństwo, rozpoznawanie

- analiza czynników głównych - (przykładem zastosowania może być diagnostyka medyczna. Jeśli na wejściu sieci zaprezentujemy objawy występujące u pacjenta, zdefiniujemy czynniki główne jako jednostki chorobowe związane z pewnymi zespołami objawów, to sieć poda na wyjściu w jakim stopniu każda z określonych jednostek chorobowych dotyczy prezentowanego zbioru objawów rozpatrywanego przypadku klinicznego.)

- kodowanie i dekodowanie

- uogólnienie

- optymalizacja - (szukanie względnego maksimum i minimum pewnej funkcji, gdy inne metody zawodzą lub sa zbyt wolne, a maks czy min globalne nie jest konieczne. Problem komiwojażera. W problemach optymalizacyjnych często wykorzystywane są sieci rekurencyjne Hopfielda. )

ZASTOSOWANIE:

- zastosowanie w sterowaniu

- pożyczki bankowe - ocena ryzyka przed udzieleniem pozyczki.

- giełda - przewidywanie zachowanai się giełdy

- rozpoznawanie pisma ręcznego

- rozpoznawanie znaków drukowanych

- walka z przestępczością (wykrywanie fałszerstw związanych z wykorzystaniem kart kredytowych.)

5. Algorytmy genetyczne, programowanie genetyczne, programowanie ewolucyjne, podstawowe pojęcia , strategie algorytmy.

ALGORYTMY GENETYCZNE

Są to algorytmy optymalizacyjne, których zasady działania oparte są na mechanizmach znanych od stuleci a mianowicie na mechanizmach doboru naturalnego i dziedziczności. Zasada przeżycia najlepszych osobników została przeniesiona wprost do algorytmów genetycznych.

Celem optymalizacji jest zwiększenie efektywności aż do osiągnięcia pewnego optimum, takiego rezultatu, który będzie najbardziej odpowiedni dla badanego przypadku.

Chromosomy są to uporządkowane zbiory genów, ciągi kodowe składające się z genów. W algorytmach genetycznych jako chromosomy będziemy rozumieli binarny ciąg kodowy.

Genem nazywamy cechę, znak, detektor. Jest to pojedynczy element genotypu a w szczególności chromosomu.

Obecnie wyróżniamy 3 metody poszukiwania: metody analityczne, metody enumeracyjne i metody losowego poszukiwania rozwiązań.

Metody enumeracyjne są to metody oparte na przeszukiwaniu całej przestrzeni rozwiązań i obliczanie dla każdego punktu wartości funkcji celu.

Dla każdego punktu w przestrzeni poszukiwań wyliczana jest wartość funkcji przystosowania. Wynikiem jest najlepszy zapamiętany rezultat.

Algorytmy genetyczne wykorzystują elementy losowego wyboru jako przewodnika w prowadzeniu wysoce ukierunkowanego poszukiwania przestrzeni rozwiązań. Takie metody poszukiwań z elementami losowego wyboru nazywamy technikami zrandomizowanymi.

Na klasyczny algorytm genetyczny, nazywanym także elementarnym lub prostym algorytmem genetycznym , składają się następujące kroki:

- inicjacja czyli wybór początkowej populacji chromosomów

- ocena przystosowania chromosomów

- sprawdzanie warunku zatrzymania,

- selekcja chromosomów,

- zastosowanie operatorów genetycznych,

- utworzenie nowej populacji

- wynik w postaci „najlepszego” osobnika.

Inicjacja, czyli utworzenie populacji początkowej, polega na wyborze żądanej liczby chromosomów reprezentowanych przez ciągi binarne określonej długości.

Ocena przystosowania chromosomów w populacji polega na obliczeniu wartości funkcji przystosowania (funkcji celu np. f(x)= x^2) dla każdego chromosomu z tej populacji. Im większa jest wartość tej funkcji, tym lepsza ”jakość” chromosomu.

Sprawdzenie warunku zatrzymania. Określenie warunku zatrzymania algorytmu genetycznego zależy od konkretnego zastosowania tego algorytmu i może nastąpić w przypadkach gdy:

- uzyskamy wartość maksymalną znaną wcześniej

- nie poprawia się uzyskiwana wartość (np. jeśli przez 3 generacje wynik się nie zmieni)

- po określonej liczbie generowanych populacji (np. przetwarzania ma trwać 6 generacji)

Selekcja chromosomów polega na wybraniu, na podstawie obliczonych wartości funkcji przystosowania, tych chromosomów, które będą brały udział w tworzeniu potomków do następnego pokolenia, czyli następnej generacji. Najczęściej stosowana jest metoda ruletki. (na podstawie wzoru wyliczany jest wycinek okręgu dla każdego chromosomu). Selekcja chromosomu może być widziana jako obrót kołem ruletki.

Do operatorów genetycznych zaliczamy krzyżowanie i mutację.

Krzyżowanie polega na wymianie informacji genetycznej (bitów) między parami chromosomów.

- kojarzymy losowo chromosomy w pracy rodziców

- dla każdej pary wybieramy losowo punkt krzyżowania

- i zamieniamy pary potomków

Mutacja polega na wymianie pojedynczego bitu w chromosomie z bardzo małym prawdopodobieństwem.

- dla każdego genu w chromosomach potomków sprawdzamy prawdopodobieństwo mutacji.

Utworzenie nowej populacji. Chromosomy otrzymane w wyniku działania operatorów genetycznych na chromosomy tymczasowej populacji rodzicielskiej wchodzą w skład nowej populacji.

Wprowadzenie najlepszego chromosomu. Jeżeli spełniony jest warunek zatrzymania algorytmu genetycznego, należy wprowadzić wynik działania algorytmu w postaci najlepszego chromosomu.

1

---