Podstawy podejmowania decyzji i inżynierii wiedzy
Pojęcie „badania systemowe”. Role i znaczenie modeli matematycznych w badaniach systemowych.
Model matematyczny to skończony zbiór symboli i relacji matematycznych oraz ścisłych zasad operowania nimi, przy czym zawarte w modelu symbole i relacje mają interpretację odnoszącą się do konkretnych elementów modelowanego wycinka rzeczywistości.
Zadanie optymalizacji i jego zastosowanie w rozwiązywaniu problemów informatycznych.
Optymalizacja to wyznaczanie przy użyciu różnych metod najlepszego, najkorzystniejszego rozwiązania problemu ze względu na wybrane kryteria. Optymalizacja skryptów będzie polegała na skróceniu czasu generowania strony, zmniejszeniu obciążenia serwera, czyli po drodze zmniejszeniu liczby zapytań do bazy danych. Bardzo ważna jest jeszcze optymalizacja kodu, która jest pierwszym krokiem do uzyskania porządnych wyników.
Optymalizacja w informatyce polega na dostosowaniu charakterystyk systemu do aktualnych wymagań aplikacji funkcjonującej na niej. Dzięki temu, z wykorzystaniem systemu o tej samej architekturze można zrealizować większą liczbę zadań.
Prawo Amdahla
Zgodnie z nim istnieje nieprzekraczalne ograniczenie przyspieszenia, które można uzyskać przez optymalizację jednego procesu.
Trzeba sobie zdać sprawę z tego, że np., jeżeli program wykorzystuje 10% czasu procesora i ograniczymy zużycie 2-krotnie, to przyspieszymy działanie tego programu, o 5% - co nie jest raczej warte wysiłku.
Wniosek, jaki się nasuwa to taki, że za pomocą prawa Amdahla (a raczej jego odwrócenia) możemy stwierdzić, kiedy proces optymalizacji nie daje zauważalnych efektów i kiedy doszło się do granicy opłacalności optymalizacji. Kolejnym stwierdzeniem jest to, że optymalizacja jednego procesu powoduje pojawienie się z innego nieoptymalnego fragmentu procesu optymalnego.
Zasada nieoznaczoności Heisenberga.
Głosi ono, że każda obserwacja jakiegoś zjawiska zakłóca jego naturalny przebieg. Dotyczy to również narzędzi, które służą do oceny działalności systemu, gdyż ich użycie powoduje dodatkowe obciążenie i wpływa na zaburzenie wyników pomiaru. Przykładem może być polecenie, vmstat w systemie BSD, które może zużywać do 10% czasu procesora.
Podstawy programowania liniowego i nieliniowego.
Programowanie liniowe to klasa problemów programowania matematycznego, w której wszystkie warunki ograniczające oraz funkcja celu mają postać liniową. Warunki ograniczające mają postać:
Mamy zmaksymalizować lub zminimalizować funkcję celu, również liniową:
Zmienne xi są liczbami rzeczywistymi.
Algorytmy metod numerycznych - interpolacja i aproksymacja, różnice między nimi. Przykład zastosowań. Podstawowe rodzaje i źródła błędów w metodach numerycznych.
Aproksymacja — zastępowanie jednych wielkości innymi, bliskimi w ściśle sprecyzowanym sensie. W skrócie: przybliżenie jednej wartości za pomocą innych.
Aproksymowaniem funkcji nazywamy przybliżanie jej za pomocą kombinacji liniowej tzw. funkcji bazowych. Funkcja aproksymująca - przybliżenie zadanej funkcji nie musi przechodzić przez jakieś zadane punkty, tak jak to jest w interpolacji.
Mówi się, że funkcja przybliżająca wygładza daną funkcję. Przybliżenie takie powoduje pojawienie się błędów, zwanych błędami aproksymacji. Dużą zaletą aproksymacji w stosunku do interpolacji jest to, że aby dobrze przybliżać, funkcja aproksymująca nie musi być wielomianem bardzo dużego stopnia (w ogóle nie musi być wielomianem - interpolacja jest szczególnym przypadkiem aproksymacji).
Przybliżenie w tym wypadku rozumiane jest jako minimalizacja pewnej funkcji błędu. Prawdopodobnie najpopularniejszą miarą tego błędu jest średni błąd kwadratowy, ale możliwe są również inne funkcje błędu, jak choćby średni błąd.
Interpolacja jeden z rodzajów aproksymacji funkcyjnej, polegający na wyznaczaniu w określonym przedziale funkcji y = f(x), która dla danych liczb
z danego przedziału przyjmuje z góry dane wartości
; dla jednoznaczności rozwiązania tego problemu żąda się dodatkowo, by funkcja f(x)) była wielomianem możliwie niskiego stopnia; gdy n = 2 (oraz
) f(x) jest funkcją liniową, co prowadzi do tzw. interpolacji liniowej.
Interpolacja liniowa szczególny przypadek interpolacji za pomocą funkcji liniowej. Jeśli x określa wartość z przedziału x0 < x < x1,a y0 = f(x0) i y1 = f(x1) tablicę wartości danej funkcji, oraz h = x1 − x0 odstęp pomiędzy argumentami, wówczas liniową interpolację wartości L(x) funkcji f otrzymujemy jako:
Błędy metod numerycznych. Numeryczne rozwiązania problemów obliczeniowych zawierają błędy. Powstają one z różnych powodów :
niedokładność modelu matematycznego (model = przybliżenie zjawiska)
niedokładność stałych fizycznych i matematycznych
błędy obliczeń
błąd zaokrągleń (1/3 = 0,33(3))
błąd reprezentacji stałych (∏ = 3,14...)
błędy obcięcia (np. zakończenie obliczeń szeregu matematycznego na konkretnym wyrazie)
błędy operacji matematycznych
błąd stosowanej metody obliczeń
Błąd BEZWZGLĘDNY
Δ = /wartość dokładna - wartość przybliżona
Błąd WZGLĘDNY
δ = (Δ/wartość poprawna) *100%
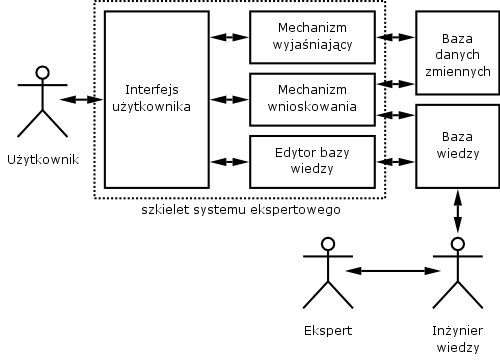
Architektura systemu ekspertowego: definicje systemu ekspertowego, metody reprezentacji wiedzy, metody pozyskiwania wiedzy, metody wnioskowania w systemach ekspertowych, elementy badania poprawności bazy wiedzy.
System ekspertowy to:
program komputerowy posiadający wiadomości w formie bazy wiedzy i przeprowadzający wnioskowanie z możliwością rozwiązywania problemów i doradztwa.
program komputerowy, który prezentuje sobą, w pewnej ściśle określonej dziedzinie, stopień doświadczenia w rozwiązywaniu problemów porównywalny ze stopniem doświadczenia i wiedzy eksperta
Cechą charakterystyczną systemu eksperckiego jest wyróżnienie reprezentacji wiedzy o dziedzinie, której dotyczy system oraz mechanizmu rozumowania na podstawie zasobów wiedzy z tej dziedziny. System ekspercki w swej strukturze zawiera takie elementy, które umożliwiają jego działanie w sposób porównywalny z najlepszymi specjalistami tzn. ma zdolność:
Zadawania pytań w celu uzyskania odpowiednich informacji od użytkownika
Wyjaśniania sposobu rozumowania na żądanie użytkownika
Uzasadniania otrzymanych konkluzji
Modyfikowania sposobu działań
W systemie eksperckim wyróżnia się następujące elementy główne :
elementy programu wykonywane podczas współdziałania użytkownika z systemem eksperckim
procedury sterowania dialogiem pomiędzy użytkownikiem systemu a systemem eksperckim
procedury wnioskowania
procedury objaśniania
procedury aktualizacji bazy wiedzy
elementy nie wykonywane stanowiące odpowiednie bazy a więc
baza wiedzy
baza danych stałych
baza danych zmiennych
W skład systemu eksperckiego wchodzą:
baza wiedzy - zawiera reprezentację wiedzy z danej dziedziny niezbędnej w procesie rozwiązywania problemów decyzyjnym. Reprezentacja wiedzy w bazie wiedzy może mieć charakter deklaratywny (reguły, fakty) lub proceduralny (procedury, funkcje)
moduł wnioskowania - zadaniem moduły jest przeszukiwanie elementów bazy wiedzy, ustalenie kolejności ich analizowania i sprawdzenie warunków ich stosowalności
baza danych stałych i baza danych zmiennych - stanowią zbiory danych (stwierdzeń) zorganizowanych według ustalonego sposobu. Baza danych zmiennych zawiera odpowiedzi użytkownika oraz wnioski pośrednie wyznaczone przez układ wnioskowania a także wykaz działań zawieszonych ze względu na brak określonych stwierdzeń w bazie
interfejs użytkownika - umożliwia prowadzenie dialogu użytkownika z systemem. Interfejs użytkownika jest często dzielony na interfejs wejściowy i wyjściowy
moduł pozyskiwania wiedzy - umożliwia pozyskiwanie i gromadzenie wiedzy w celu zwiększenia efektywności systemu
moduł objaśniania - uzasadnia decyzje podejmowane przez moduł wnioskowania systemu eksperckiego poprzez przedstawienie toku rozumowania
METODY POZYSKIWANIA WIEDZY:
bezpośrednie zapisywanie wiedzy tzn. uczenie na pamięć. Metoda ta nie wymaga żadnego działania typu wnioskowanie lub transformowanie wiedzy od uczącego się systemu
pozyskiwanie wiedzy na podstawie instrukcji. Metoda ta wymaga udziału nauczyciela w procesie pozyskiwania wiedzy i polega na wykorzystaniu źródeł wiedzy wskazanych przez nauczyciela oraz przekształceniu wiedzy do postaci akceptowalnej przez system
pozyskiwanie wiedzy na podstawie analogii. Metoda ta polega na przekształceniu istniejącej wiedzy w bazie wiedzy w celu umożliwienie opisu faktów podobnych do faktu opisanego uprzednio
pozyskiwanie wiedzy na podstawie przykładów. Jest to szczególny przypadek uczenia indukcyjnego. Polega na generowaniu ogólnego opisu pojęć na podstawie zbioru przykładów oraz kontrprzykładów obiektów reprezentujących te pojęcia. Przykłady mogą być określone przez eksperta na podstawie wcześniej utworzonych baz danych
pozyskiwanie wiedzy na podstawie odkrywania i obserwacji. Metoda ta jest często nazywana uczeniem bez nauczyciela i stanowi ogólny przypadek uczenia indukcyjnego który wymaga zwiększonego udziału uczącego w procesie uczenia.
METODY REPREZENTACJI WIEDZY - to metody zapisania pozyskanej wiedzy w maszynach cyfrowych, w sposób najbliższy sposobowi rozumowania człowieka. P
powinna umożliwiać prosty, kompletny (wyczerpujący), zwięzły, zrozumiały i wyraźny zapis wiedzy.
metody bazujące na bezpośrednim zastosowaniu logiki takie jak: rachunek zadań, rachunek predykatów
metody wykorzystujące zapis stwierdzeń
metody bazujące na sieciach semantycznych
metody wykorzystujące systemy regułowe i zapis reguł
ramy
tabele decyzyjne
drzewa decyzyjne
metody przybliżonej reprezentacji wiedzy.
Podział reprezentacji wiedzy ze względu na techniki zapisu wiedzy :
reprezentacja proceduralna - polega na określeniu zbioru procedur których działanie reprezentuje wiedzę o dziedzinie
reprezentacja deklaratywna - zbiór specyficznych dla danej dziedziny faktów stwierdzeń i reguł(wykłady Piłota)
Wnioskowanie - proces, w którym na podstawie zadań uznanych za prawdziwe dochodzi się do nowego zdanie dotąd nieuznanego (konkluzji).
METODY WNIOSKOWANIA
wnioskowanie logiczne
dedukcja
abdukcja
indukcja
wnioskowanie na bazie niespójności
wnioskowanie nie monotoniczne
wnioskowanie pochodne od logiki
wstecz
wprzód
mieszane
algorytmy dopasowania wzorca
metody szukania
wnioskowanie przez analogię
metody uczenia parametrycznego i strukturalnego
Ze względu na metodę prowadzenia procesu wnioskowania systemy ekspertowe dzieli się na:
z logiką dwuwartościową (Boole'a),
z logiką wielowartościową,
zlogiką rozmytą.
Ze względu na rodzaj przetwarzanej informacji systemy ekspertowe dzielą się na dwie grupy:
systemy z wiedzą pewną, czyli zdeterminowaną,
systemy z wiedzą niepewną, w przetwarzaniu, której wykorzystuje się przede wszystkim aparat probabilistyczny.
BADANIA POPRAWNOŚCI BAZY WIEDZY
Spójność - wykrywanie reguł zbędnych, sprzecznych, pochłaniających, ze sprzecznym warunkiem oraz zapętlonych, kompletność bazy reguł - poszukiwanie reguł brakujących.
Spójność reguł:
Sprzeczność: dwie reguły są sprzeczne, jeśli ich części warunkowe są równocześnie spełnione lub nie spełnione we wszystkich możliwych przypadkach oraz ich konkluzje są różne. Przykład: (a,L) ^ (c, 3)=>(d,H), (a,L) ^ (c, 3) =>(d,L)
Reguły pochłaniające - jedna reguła jest pochłaniana wówczas, gdy część warunkowa pierwszej reguły jest spełniona, jeśli jest spełniona część warunkowa drugiej reguły i konkluzje obu reguł są identyczne. Przykład: (a,L) ^ (c, 3)=>(d,H), (c,3)=>(d,H)
Niepotrzebne warunki: dwie reguły mają niepotrzebne warynki, jeśli obie są pochłaniane przez trzecią regułę. Przykład: (a,L)^(b,D)^(c,5)=>(d,H), (a,R)^(b,D)^(c,5)=>(d,H).
Zapętlenie reguł: Zestaw reguł tworzy pętlę jeśli zapętlenie tych reguł jest cykliczne. Przykład: (a,L)^(c,5)=>(d,H), (d,H)=>(f,2), (f,2)^(g,4)=>(c,5)
Wielokrotne odwoływanie do jednego atrybutu: Występuje wtedy, gdy w części warunkowej są człony zawierające ten sam atrybut. Przykład: (a,L)^(a,R)=>(d,H)
Teoria zbiorów rozmytych - definicje zbioru, liczby i przykłady operacji, przykład wnioskowania rozmytego.
Teoria zbiorów rozmytych jest uogólnieniem klasycznej teorii zbiorów. Teoria klasyczna mówi ze element należy bądź nie należy do zbioru. Czyli funkcja przynależności według klasycznej teorii zbiorów może przyjmować tylko wartość 0 lub 1. W teorii zbiorów rozmytych element może częściowo należeć do jakiegoś zbioru a przynależność tę można wyrazić z pomocą liczby rzeczywistej z zakresu 0 do 1Tojęcie ZBIORÓW ROZMYTYCH jako uogólnienie zbiorów zwykłych (nie rozmytych) zostało wprowadzone przez L. Zadehaw w 1965r. Tradycyjny sposób reprezentowania elementu x zbioru A odbywa się za pośrednictwem funkcji charakterystycznej μ(x) równej jeden, gdy element należy do zbioru A lub zero gdy element nie należy do tego zbioru. W systemach rozmytych element może należeć do każdego zbioru częściowo. Stopień przynależności do zbioru A stanowiący uogólnienie funkcji charakterystycznej jest zwany funkcją przynależności μ(x), przy czym μ(x) ∈ [0, 1]
Operacje na liczbach rozmytych
Wprowadźmy definicję liczby rozmytej (Zadeh 1965).
Definicja. Liczbą rozmytą A nazywamy zbiór rozmyty określony na zbiorze liczb rzeczywistych R co zapisujemy:
A ⊆ R., μ: R → [0,1]
Podstawowe operacje na liczbach rozmytych można zdefiniować stosując zasadę rozszerzania (Zadeh 1965):
Definicja. Niech dana będzie pewna operacja dwuargumentowa na
liczbach rzeczywistych:
* : R x R → R
Ponadto, niech A i B będą liczbami rozmytymi A, B ⊆ R, wtedy operację `*' można rozszerzyć na argumenty rozmyte A i B w następujący sposób:
μ(z) = min {μ(x), μ(y)}
OPERACJE NA ZBIORACH ROZMYTYCH
Suma logiczna A ∪ B
μ(x) = μ(x) ∪ μ(y) = Max [A(x), B(x)]
gdzie znak ∪ oznacza operator Max
przykład:
A= {, , , }
B= {, , , }
C = A ∪ B
C = {, , , }
Iloczyn logiczny zbiorów A ∩B
μ∩ (x) = μ(x) ∩ μ(x) = Min [A(x), B(x)]
przy czym symbol ∩ oznacza operator Min
C = A ∩B
C = {, , , }
Negacja zbioru A
μ(x) = 1 - μ(x)
w odróżnieniu od zbiorów zwykłych gdzie negacja elementów należących do zbioru tworzyła zbiór pusty, negacja w odniesieniu do zbiorów rozmytych definiuje zbiór niepusty o elementach z funkcjami przynależności należącymi również do przedziału
[0, 1]
Równość zbioru A i B
Zbiory rozmyte A(x) i B(x) są sobie równe, gdy dla wszystkich elementów xi obu zbiorów zachodzi μ(xi) = μ(xi)
Operacja koncentracji CON(A)
μ(x) = [μ(x)]²
jest to szczególnie często używana operacja w działaniach na zmiennej lingwistycznej gdzie utożsamia się ja z intensyfikatorem „bardzo”
Operacja rozciągania DIL(A)
μ(x) = [μ(x)]
operacja ta w znaczeniu lingwistycznym oznacza „mniej więcej”
Iloczyn algebraiczny A*B
μ(x) = μ(x) * μ(x)
Suma ograniczona dwu zbiorów rozmytych A|+|B
μ(x) = min {1, μ(x) + μ(x)}
Różnica ograniczona dwu zbiorów rozmytych A|-|B
μ(x) = max {0, μ(x) - μ(x)}
Iloczyn ograniczony dwu zbiorów rozmytych A|*|B
μ(x) = max {0, μ(x) + μ(x) - 1}
Normalizacja zbioru NORM(A)
μ(x) =
Zbiór A zawiera się w zbiorze B to jest A⊂B jeśli dla wszystkich elementów zachodzi nierówność:
μ(xi) ≤ μ(xi)
Zbiory rozmyte (ang. fuzzy sets) są wykorzystywane do formalnego określania nieostrych, nieprecyzyjnych lub wieloznacznych pojęć, np. "wysokie drzewo", "piękny krajobraz", itd. Mają one swoje źródło w rozwoju teorii sterowania, teorii systemów i zw. logik wielowartościowych. Zauważono, bowiem, że chociaż umysł ludzki jest zdolny do rozumowania w kategoriach przybliżonych, to mimo to jest w stanie przetwarzać dane przybliżone i niejednoznaczne oraz wyznaczać przybliżone rozwiązania, czego nie są w stanie zrobić komputery działające w oparciu o ścisłe reguły. W teorii zbiorów rozmytych funkcja charakterystyczna została uogólniona i nazywa się funkcją przynależności. Przyporządkowuje ona każdemu elementowi zbioru wartości z przedziału [0,1], zamiast tylko jedną z wartości z dwuelementowego zbioru {0,1}, jak to jest w klasycznej teorii zbiory.
Logiczną podstawą pojęcia podzbioru rozmytego jest logika wielowartościowa. Podzbiór rozmyty umożliwia opisanie pojęć, których granica między posiadaniem pewnej własności i jej brakiem jest rozmyta.
Zadania realizowane przez sieci neuronowe - architektura przykładowych sieci i metody uczenia.
SIEĆ NEURONOWA - jest równoległym systemem wieloprocesorowym, zorganizowanym na wzór struktur przetwarzania w biologicznej sieci neuronowej (w mózgu człowieka). Podstawowym elementem tej sieci jest prosty procesor dokonujący dwuwartościowej selekcji sumarycznego pobudzenia wejść i wytwarzający jedno z alternatywnych wyjść odpowiadających pobudzeniu podprogowemu i ponad progowemu. Wielkość pobudzenia jest funkcją wag poszczególnych wejść, w procesie uczenia wartości wag są modyfikowane. Procesor realizujący taką funkcję jest nazywany neuronem, przez analogię do sieci biologicznej.
ZADANIA REALIZOWANE PRZEZ SIECI NEURONOWE
Rozpoznawanie wzorców (znaków, liter, kształtów, sygnałów mowy, sygnałów sonarowych) Klasyfikowanie obiektów
Prognozowanie i ocena ryzyka ekonomicznego
Prognozowanie zmian cen rynkowych (giełdy, waluty)
Ocena zdolności kredytowej
Ocena wniosków ubezpieczeniowych
Rozpoznawanie wzorów podpisów
Prognozowanie zapotrzebowania na energię elektryczną
Diagnostyka medyczna
Dobór pracowników
Prognozowanie sprzedaży
Analizowanie zachowań klienta w supermarketach
Aproksymowanie wartości funkcji
METODY UCZENIA SIECI
Uczenie pod NADZOREM
Przy tym uczeniu każdemu wektorowi wejściowemu towarzyszy zadany wektor wyjściowy. Dane uczące są podane w postaci par uczących.
Celem uczenia pod nadzorem minimalizacja odpowiednio zdefiniowanej funkcji celu, która w wyniku umożliwi dopasowanie wartości aktualnych odpowiedzi neuronów wyjściowych do wartości żądanych dla wszystkich par uczących.
Uczenie z KRYTYKIEM
Uczenie z krytykiem jest odmianą uczenia pod nadzorem, w którym nie występuje informacja o wartościach żądanych na wejściu systemu a jedynie informacja czy podjęta przez system akcja daje wyniki pozytywne w sensie pożądanego zachowania systemu czy negatywne.
Uczenie samoorganizujące się typu HEBBA
W modelu Hebba wykorzystuje się wynik obserwacji neurobiologicznych zgodnie, z którymi waga powiązań między dwoma neuronami wzrasta przy jednoczesnym stanie pobudzenia obu neuronów w przeciwnym wypadku maleje.
Uczenie samoorganizujące się typu KONKURENCYJNEGO
W uczeniu typu konkurencyjnego neurony współzawodniczą ze sobą, aby stać się aktywnymi (pobudzonymi). W odróżnieniu do uczenia Hebba gdzie dowolna liczba neuronów może być aktywna w uczeniu konkurencyjnym tylko jeden z neuronów może być aktywny a pozostałe pozostają w stanie spoczynku z tego powodu uczenie to nosi tez nazwę WTA (Winner Takes All). Uczenie typu WTA nie wymaga nauczyciela i odbywa się zwykle z zastosowaniem znormalizowanych wektorów wyjściowych
Uczenie metodą wstecznej propagacji błędów:
Pierwszą czynnością w procesie uczenia jest przygotowanie dwóch ciągów danych: uczącego i weryfikującego. Ciąg uczący jest to zbiór takich danych, które w miarę dokładnie charakteryzują dany problem. Jednorazowa porcja danych nazywana jest wektorem uczącym. W jego skład wchodzi wektor wejściowy, czyli te dane wejściowe, które podawane są na wejścia sieci i wektor wyjściowy, czyli takie dane oczekiwane, jakie sieć powinna wygenerować na swoich wyjściach. Po przetworzeniu wektora wejściowego, nauczyciel porównuje wartości otrzymane z wartościami oczekiwanymi i informuje sieć czy odpowiedź jest poprawna, a jeżeli nie, to, jaki powstał błąd odpowiedzi. Błąd ten jest następnie propagowany do sieci, ale w odwrotnej niż wektor wejściowy kolejności (od warstwy wyjściowej do wejściowej) i na jego podstawie następuje taka korekcja wag w każdym neuronie, aby ponowne przetworzenie tego samego wektora wejściowego spowodowało zmniejszenie błędu odpowiedzi. Procedurę taką powtarza się do momentu wygenerowania przez sieć błędu mniejszego niż założony. Wtedy na wejście sieci podaje się kolejny wektor wejściowy i powtarza te czynności. Po przetworzeniu całego ciągu uczącego (proces ten nazywany jest epoką) oblicza się błąd dla epoki i cały cykl powtarzany jest do momentu, aż błąd ten spadnie poniżej dopuszczalnego. Jak to już było zasygnalizowane wcześniej, SSN wykazują tolerancję na nieciągłości, przypadkowe zaburzenia lub wręcz niewielkie braki w zbiorze uczącym. Jest to wynikiem właśnie zdolności do uogólniania wiedzy.
Algorytm uczenia Kohonena:
Sieć Kohonena posiada tylko dwie warstwy: warstwę wejściową oraz warstwę wyjściową, składającą się z neuronów radialnych. Warstwa ta znana jest również jako warstwa tworząca mapę topologiczną, ponieważ takie jest jej najczęstsze zastosowanie. Neurony w warstwie tworzącej mapę topologiczną są rozważane w taki sposób, jakby były rozmieszczone w przestrzeni według jakiegoś ustalonego wzoru.
Sieci Kohonena uczone są przy wykorzystaniu algorytmu iteracyjnego. Rozpoczynając od początkowych, wybranych w sposób losowy centrów radialnych, algorytm stopniowo modyfikuje je w taki sposób, aby odzwierciedlić skupienia występujące w danych uczących.
Siec Hopfielda:
Strukturę sieci Hopfielda można opisać bardzo prosto - jest to układ wielu identycznych elementów połączonych metodą każdy z każdym. Jest, zatem najczęściej rozpatrywana jako struktura jednowarstwowa. W odróżnieniu od sieci warstwowych typu perceptron sieć Hopfielda jest siecią rekurencyjną, gdzie neurony są wielokrotnie pobudzane w jednym cyklu rozpoznawania, co uzyskuje się poprzez pętle sprzężenia zwrotnego.
Wagi połączeń wyliczane są w sieci Hopfielda a priori, jej faza uczenia ogranicza się do wyliczenia wartości wag zgodnie zasadą uczenia Hebba.
Podstawy podejmowania decyzji i inżynierii wiedzy
1
Wyszukiwarka
Podobne podstrony:
Wykład 5 - Podstawy podejmowania decyzji, Podstawy zarządzania(1)
D Podstawy podejmowania?cyzji i inżynierii wiedzy
Podstawowe elementy planowania i podejmowania decyzji
TEORIA PODEJMOWANIA DECYZJI NA PODSTAWIE FIRMY PROFAST
Ściąga TiPPDK cz2, Zarządzanie i inżynieria produkcji, Semestr 8, Teoria i praktyka podejmowania dec
Ściąga TiPPDK cz1, Zarządzanie i inżynieria produkcji, Semestr 8, Teoria i praktyka podejmowania dec
6. Planowanie i podejmowanie decyzji - podstawy zarządzania, I semestr, Prace, podstawy zarządzania
PODEJMOWANIE DECYZJI, PODSTAWY ZARZĄDZANIA
TiPPDK - moj projekt[1], Zarządzanie i inżynieria produkcji, Semestr 8, Teoria i praktyka podejmowan
Noworyta-zagadnienia do egzaminu, podstawy inżynierii chemicznej, zagadnienia z inż
i 31 2 Podejmowanie decyzji w organizacji - problemy podstawowe, na studia, procesy decyzyjne
i 31 0 Podejmowanie decyzji w organizacji problemy podstawowe
5. Podejmowanie decyzji - st[1], Materiały PSW Biała Podlaska, Podstawy zarządzania- ćwiczenia
podejmowanie-decyzji-menagerskich, Podstawy zarządzania
Planowanie i podejmowanie decyzji, Wojskowa Akademia Techniczna - Zarządzanie i Marketing, Licencjat
Zagadnienia na egzamin z Podstaw wiedzy o państwie i prawie1
więcej podobnych podstron