Laboratorium Technik Cyfrowych nr 2
Projektowanie układów logicznych jest ważnym i zarazem trudnym zagadnieniem. Możemy je wykonać np. w następujące sposoby:
Bezpośrednio wg tabeli prawdy.
Minimalizując funkcję algebraicznie.
Metodą tabeli Karnaugha zaznaczając grupy jedynek.
Metodą tabeli Karnaugha zaznaczając grupy zer.
Dowolną metodą z powyższych, przedstawiając rozwiązanie za pomocą jednego rodzaju bramek.
Podstawową rzeczą zatem jest stworzenie tabeli prawdy, z której korzystamy niezależnie od wybranego przez nas sposobu. Pierwszy sposób jest oczywiście najprostszym i zarazem najgorszym rozwiązaniem. Minimalizacja funkcji algebraicznie nie jest łatwa jednakże, jeśli biegle korzystamy z praw i twierdzeń algebry Boole`a, może być bardzo szybką metodą.
Tablice Karnaugha są wygodnym sposobem zapisu funkcji ze względu na łatwość minimalizacji. Dla każdej kombinacji zmiennych do kratek tablicy wpisujemy wartość funkcji: „1”, „0”, a gdy funkcja jest nieokreślona „x” lub „ - ”. Zmienne wejściowe są zapisywane za pomocą kodu Grey'a (a nie systemem dwójkowym), dzięki czemu sąsiednie komórki różnią sie tylko jednym bitem. Ma to znaczenie podczas minimalizacji formuł Boolowskich.
Wykorzystujemy tu regułę sklejania:
Z tego wynika, ze sąsiednie zmienne różniące sie jednym bitem mogą zostać zredukowane.
Postać dysjunkcyjna - zaznaczamy jak największe grupy pól zawierających tylko jedynki, przy czym:
ilość pól w grupie ma być potęga dwójki: 1,2,4,8,...
łączymy tylko pola sąsiadujące lub pola oddzielone krawędzią tablicy
dodatkowo można łączyć pola leżące symetrycznie względem osi symetrii w dwóch częściach diagramu.
wybieramy takie grupy, aby zawierały wszystkie jedynki co najmniej raz (w obrębie kilku grup ta sama jedynka może sie powtarzać). Ilość pól które zawiera pojedyncza grupa ma być jak największa, a łączna ilość grup jak najmniejsza. Zapewnia to minimalizacje formuły.
w przypadku występowania znaków nieokreśloności można (nie jest to konieczne) połączyć je z jedynkami lub zerami. Otrzymamy dzięki temu prostszą formułę, gdyż większy obszar opisuje mniej zmiennych.
Zapis formuły Boolowskiej w przypadku postaci dysjunkcyjnej (suma iloczynów):
Formule zapisujemy w postaci sumy iloczynów. W skład iloczynów wchodzą zmienne wejściowe, które w obrębie jednej grupy maja stała wartość. Gdy zmienna wynosi jeden - nie negujemy tej zmiennej wpisując ją do iloczynu, dla wartości zero - zapisujemy postać zanegowaną.
Postać koniunkcyjna
różni sie od postaci dysjunkcyjnej tym, ze grupujemy zera, oraz ze formułę zapisujemy w postaci iloczynu sum. Zmienne mające stałą wartość negujemy, gdy ich wartość wynosi jeden, dla wartości zero zapisujemy postać niezanegowana.
Zjawisko hazardów
Rzeczywiste bramki zmieniają swój stan z pewnym opóźnieniem. Nazywamy go czasem propagacji bramki. W niektórych przypadkach takie opóźnienie może być niekorzystne. Najprostszym przykładem są wyrażenia: a + a' (równolegle polaczenie styków zwiernego i rozwiernego) oraz aa' (polaczenie szeregowe). Jeżeli zwarcie styku zwiernego i rozwarcie styku rozwiernego (lub odwrotnie) następuje równocześnie, to pierwsze wyrażenie jest równe jedności a drugie zeru także podczas zmiany stanu przekaźnika. Jeżeli jednak czasy, w których następuje zmiana stanu będą różne, to pierwsze z wyrażeń może przybrać wartość zero, a drugie wartość jeden. Zjawisko to nazywamy hazardem.
Hazardy dzielą sie na statyczne i dynamiczne:
Statyczne - kiedy wyjście, które nie ma zmienić stanu krótkotrwale zmienia stan na przeciwny: w zerze kiedy wyjście ma pozostać w 0, w jedynce - gdy wyjście ma pozostać w 1.
Dynamiczne - kiedy występują wielokrotne zmiany stanów na wyjściach które zmieniają stan.
Hazardy mogą w określonych przypadkach powodować nieprawidłowe działanie układów (jeżeli wyjścia, na których pojawiają sie hazardy sż interpretowane asynchronicznie) .
Usuwanie hazardów w sieci dwupoziomowej:
Aby usunąć hazardy w postaci dysjunkcyjnej, należy sprawdzić w tablicy Karnaugha czy wszystkie przylegające jedynki są pokryte wspólna grupa. Jeżeli nie to należy dodać dodatkowe grupy. Aby usunąć hazardy w postaci koniunkcyjnej, należy sprawdzić w tablicy Karnaugha czy wszystkie przylegające zera maja wspólne grupy. Jeśli nie to również należy dodać dodatkowe grupy.
Przykład hazardu statycznego w jedynce:
|
AB |
00 |
01 |
11 |
10 |
CD |
|
|
|
|
|
00 |
0 |
0 |
|
1 |
|
01 |
|
1 |
1 |
1 |
|
11 |
1 |
1 |
0 |
0 |
|
10 |
0 |
0 |
0 |
0 |
|
Rozwiązania zadań:
Zaprojektuj dwuwejściowy układ logiczny realizujący działanie określone następującą tabelą prawdy:
p |
q |
Y |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
Bezpośrednio wg tabeli prawdy:
Y= (~p * ~q) + (~p * q) + (p * q)
Minimalizując funkcję algebraicznie:
Y= (~p * ~q) + (~p * q) + (p * q)
Y= (~p * ~q) + (~p + p) * q
Y= (~p * ~q) + q
Y= (p nor q) + q
Metodą tabeli Karnaugha zaznaczając grupy jedynek.
p\q |
0 |
1 |
0 |
|
|
1 |
0 |
1 |
Y= ~p + q
Metodą tabeli Karnaugha zaznaczając grupy zer.
p\q |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
Y= ~p + q
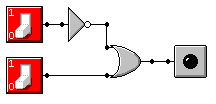
Dowolną metodą z powyższych, przedstawiając rozwiązanie za pomocą jednego rodzaju bramek.
Z podpunktu 2) Y= (p nor q) + q = [(p nor q) nor q] nor [(p nor q) nor q]
Zaprojektuj dwuwejściowy układ logiczny realizujący działanie określone następującą tabelą prawdy:
Zbuduj trzywejściowy układ, który przyjmuje wartość 1 wówczas, gdy co najmniej dwa spośród wejść przyjmują wartość jeden.
Zaprojektuj trzywejściowy układ logiczny realizujący działanie określone następującą tabelą prawdy:
Zaprojektuj trzywejściowy układ logiczny realizujący działanie określone następującą tabelą prawdy:
Zaprojektuj trzywejściowy układ logiczny realizujący działanie określone następującą tabelą prawdy:
Za pomocą tabeli Karnaugha możliwe jest szybkie znalezienie odpowiedniej formuły opisującej układ.
Formuła odczytana z tabeli Karnaugha rzadko jest rozwiązaniem optymalnym.
Podczas tworzenia tabeli ważnym jest odpowiednie zakreślanie grup, tak aby było każda z nich była maksymalnie duża, a zarazem liczba grup była jak najmniejsza.
Tworzenie grup zawierających w sobie inne grupy jest bezcelowe.
W zależności od układu należy rozważyć użycie postaci dysjunkcyjnej lub koniunkcyjnej, w zależności od tego, która da prostszy (bardziej optymalny) układ.
Próba utworzenia układu zbudowanego z jednego typu bramek może sprowadzić układ do postaci bardziej optymalnej (jednak nie musi).
p |
q |
Y |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
|
p\q |
0 |
1 |
|
0 |
|
1 |
|
1 |
0 |
0 |
|
Y= ~p
p |
q |
r |
Y |
||||||
0 |
0 |
0 |
0 |
||||||
0 |
0 |
1 |
0 |
||||||
0 |
1 |
0 |
0 |
||||||
0 |
1 |
1 |
1 |
||||||
1 |
0 |
0 |
0 |
||||||
1 |
0 |
1 |
1 |
||||||
1 |
1 |
0 |
1 |
||||||
1 |
1 |
1 |
1 |
||||||
p \ qr |
00 |
01 |
11 |
10 |
|||||
0 |
0 |
0 |
|
0 |
|||||
1 |
0 |
|
|
1 |
|||||
Y= q * r + p * r + p * q
p |
q |
r |
Y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
p \ qr |
00 |
01 |
11 |
10 |
0 |
|
0 |
|
0 |
1 |
0 |
|
0 |
0 |
Y= (~p * ~q * ~r) + (p * ~q * r) + (~p * q * r)
Y= (~p * ~q * ~r) + r * (p * ~q + ~p * q)
Y= (~p * ~q * ~r) + r * (p XOR q)
p \ qr |
00 |
01 |
11 |
10 |
||||
0 |
|
1 |
1 |
1 |
||||
1 |
0 |
1 |
|
1 |
||||
p |
q |
r |
Y |
|||||
0 |
0 |
0 |
0 |
|||||
0 |
0 |
1 |
1 |
|||||
0 |
1 |
0 |
1 |
|||||
0 |
1 |
1 |
1 |
|||||
1 |
0 |
0 |
0 |
|||||
1 |
0 |
1 |
1 |
|||||
1 |
1 |
0 |
1 |
|||||
1 |
1 |
1 |
0 |
|||||
Y= (q + r) * (~p + ~q + ~r)
Y= (q + r) * ~(p * q * r)
p |
q |
r |
Y |
|||||
0 |
0 |
0 |
0 |
|||||
0 |
0 |
1 |
0 |
|||||
0 |
1 |
0 |
0 |
|||||
0 |
1 |
1 |
0 |
|||||
1 |
0 |
0 |
0 |
|||||
1 |
0 |
1 |
0 |
|||||
1 |
1 |
0 |
1 |
|||||
1 |
1 |
1 |
1 |
|||||
p \ qr |
00 |
01 |
11 |
10 |
||||
0 |
0 |
0 |
0 |
0 |
||||
1 |
0 |
0 |
|
1 |
||||
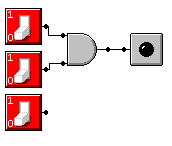
Y= p * q
Wnioski:
Damian Pawlik
WFMiIS
grupa 21
AB + AB' = A( B + B' ) = A lub (A + B) (A + B') = A
Postać dysjunkcyjna (kolor niebieski): y = AC' + A'D.
Przy przejściu z 0101 do 1101 występuje hazard.
W tablicy Karnaugh komórki 0101 i 1101 sąsiadują ze sobą, lecz nie są objęte wspólnym implikantem. To powoduje pojawienie sie hazardu. Dodajemy dodatkowy implikant C'D (kolor czerwony), aby go wyeliminować. Ostatecznie funkcja ma postać: y = AC' + A'D + C'D
~p + p 1
~p * ~q p nor q
(~p * ~q * ~r) NOR z 3 wejściami
(~p + ~q + ~r) NAND z 3 wejściami
p nor p ~p * ~p ~p
Wyszukiwarka
Podobne podstrony:
AIP Lab2 Spr
lab2 spr
lab2 spr
lab2 spr
SPR-ANKI, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab2
NiSHiP spr lab2 MS i MT id 3201 Nieznany
spr lab2
SPRBogdan Racięga IMiU spr. LAB2
spr tst lab2, Mechatronika AGH IMIR, rok 2, Teoria sterowania, lab2 grzybek
moje spr, lab2, Nr ćwiczenia
spr lab2 PA, AGH WIMIR AiR, Semestr 5, Sterowanie dyskretne, projekt SD NAW, z zajec, sprawko lab2 P
spr lab2 PA wer drugostronna
Spr[1] adm i uznanie adm
08 03 KPGO Spr z realizacji
17 Rozp Min Zdr w spr szk czyn Nieznany
I9M1S1 Nawrot Gudanowicz lab2
więcej podobnych podstron