Laboratorium Podstaw automatyki
temat: Matlab i Simulink
Mechatronika	gr. dz. Ib	gr. lab. 3	18.03.2009r

1. Wstęp teoretyczny:

Matlab - Nazwa programu pochodzi od angielskich słów MATrix LABoratory, gdyż początkowo program ten był przeznaczony do numerycznych obliczeń macierzowych. Obecnie program ten potrafi znacznie więcej, cechuje go duża liczba funkcji bibliotecznych oraz duże możliwości rozbudowy przez użytkownika za pomocą pisania własnych funkcji. Posiada on swój język programowania, co umożliwia pisanie w pełni funkcjonalnych programów działających w środowisku Matlaba.

W zakresie grafiki Matlab umożliwia rysowanie dwu i trójwymiarowych wykresów funkcji oraz wizualizację wyników obliczeń w postaci rysunków statycznych i animacji. Możliwe jest pobieranie danych pomiarowych z urządzenia zewnętrznego przez porty w celu ich obróbki. Wszystko to powoduje, że program ten znajduje bardzo szerokie zastosowanie.

Simulink - jest częścią pakietu matematycznego MATLAB firmy The MathWorks i służy do przeprowadzania symulacji komputerowych. Simulink pozwala budować modele symulacyjne przy pomocy interfejsu graficznego i tzw. bloków. Przy pomocy Simulinka można przeprowadzać zarówno symulacje z czasem dyskretnym jak i ciągłym.

Simulink znajduje głównie zastosowanie (poprzez to, że umożliwia symulacje w czasie ciągłym) w cyfrowym przetwarzaniu sygnałów, analizie obwodów elektrycznych i teorii sterowania

2. 
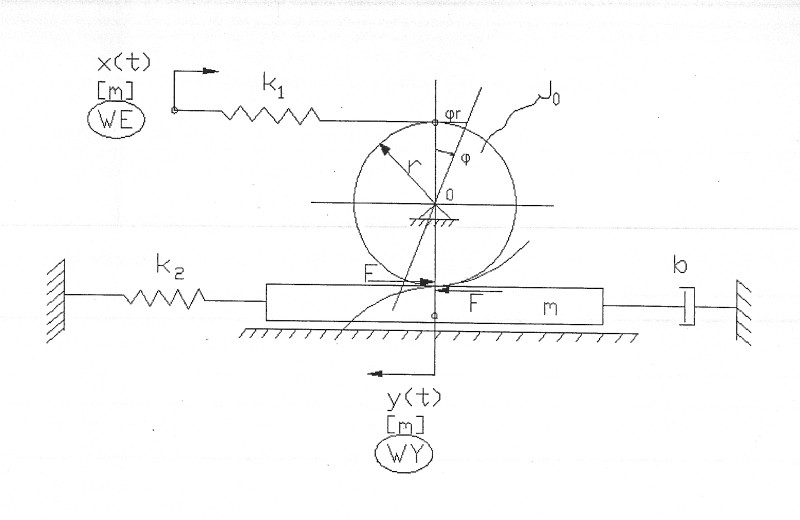
   Opis wykonanego zadania

Rys. 1 - schemat badanego układu

a) Cele ćwiczenia:

- określenie transmitancji operatorowej przy pomocy programu MATLAB

- zamodelowanie działania układu o danej transmitancji operatorowej pomocy

programu SIMULINK

b) Ręczny sposób obliczania transmitancji operatorowej :

3. Wyznaczanie transmitancji oraz modelowanie układu

1. Wyznaczenie transmitancji operatorowej

Do obliczenia transmitancji operatorowej układu w programie MATLAB użyto następujących poleceń:

- printsys(L,M) - wyświetla wyznaczoną transmitancję operatorową układu dla zdefiniowanych wartości L i M, gdzie L jest licznikiem wzoru na transmitancje K(s)=Y(s)/X(s), a M jest mianownikiem tego wzoru.

- bode(L,M) - wykreśla wykres Bode'a dla podanych wartości L i M (gdzie L- licznik [Y(s)] , M- mianownik [X(s)], transmitancji operatorowej K(s)). Wykres Bode'a logarytmiczna zależność amplitudy i fazy od częstotliwości, wyznaczona dla obiektu automatyki lub układu elektronicznego opisanego transmitancją operatorową.

- nyquist(L,M) - wykreśla wykres Nyquist'a dla podanych wartości L i M. Wykres Nyquist'a zwany też charakterystyką amplitudowo-fazową w automatyce, wykres transmitancji widmowej układu na płaszczyźnie zmiennej zespolonej.Można ją wyznaczyć doświadczalnie, dokonując pomiarów (w stanie ustalonym) amplitudy oraz przesunięcia fazowego sygnału wyjściowego układu, gdy sygnałem wejściowym jest sygnał sinusoidalny o stałej amplitudzie i częstotliwości. Na wykresie umieszcza się punkty odpowiadające wartościom transmitancji widmowej dla kolejnych wartości pulsacji
. Kierunek strzałki oznacza kierunek wzrostu ω. Na osi rzędnych odłożona zostaje wartość części urojonej, a na osi odciętych wartość części rzeczywistej transmitancji widmowej. Wykres charakterystyki amplitudowo-fazowej układu realizowalnego fizycznie dąży do początku układu współrzędnych. Składa się z dwóch wykresów: charakterystyki amplitudowej oraz charakterystyki fazowej.

- step(L,M) - wyznacza odpowiedź skokową układu (zdefiniowanego transmitancją operatorową)

- impulse(L,M) - wyznacza odpowiedź impulsową układu (zdefiniowanego transmitancją operatorową)

Kod programu:

% DANE

Jo=2.5;

m=5;

r=0.3;

k1=10000;

k2=7000;

b=67;

L=[k1]

M=[(Jo/r^2+m) b (k1+k2)];

printsys(L,M)

subplot(2,2,1)

bode(L,M)

grid

subplot(2,2,2)

nyquist(L,M)

subplot(2,2,3)

step(L,M)

grid

subplot(2,2,4)

impulse(L,M)

grid

2. Modelowanie układu

4. Wyznaczanie nastawień regulatora PID metodą Zieglera-Nicholsa

a) Ręczny sposób wyznaczania nastawień regulatora PID

- ustawienie regulatora PID na działanie tylko proporcjonalne, dzięki czemu uda się wyznaczyć granicę stabilność układu K_kr (dla naszego układu K_kr>320)

- wprowadzając K_kr uzyskamy odpowiedź dla granicy stabilności, z wykresu której odczytujemy T_kr (dla naszego układu T_kr=1.98)

- obliczamy nastawy regulatora PID wg wzoru

Kp = 0.2*K_kr

Ti = 0.33*T_kr

Td = 0.5*T_kr

b) Program w MATLAB'ie do wyznaczania nastaw regulatora PID

clear all;

clc;

clf;

% TRANSMITANCJA OBIEKTU

L1=[0.5];

M1=[1 20 10 40];

clc;

disp(`transmitancja operatorowa obiektu')

tf(L1,M1)

% TRANSM. UKL. BEZ REGULATORA

[L2,M2]=cloop(L1,M1,-1);

subplot(4,1,1)

impulse(L2,M2)

legend(`uklad bez regulatora')

t=[0:0.01:20];

[y1,x,t]=impulse(L2,M2,t)

grid

% ODPOWIEDZ UKLADU Z WZOCNIENIEM Kkr

Kkr=320;

[L3,M3]=cloop(Kkr*L1,M1,-1);

subplot(4,1,2)

impulse(L3,M3)

legend(`uklad na grabnicy stabilnosci')

grid

% WYZNACZENIE NASTAW REG. PID

Tkr=4.5-2.52;

Kp=0.2*Kkr;

Ti=0.33*Tkr;

Td=0.5*Tkr;

% TRANSMITANCJA REG. PID

[Lr,Mr]=parallel([0 1],[Ti 0],[0 1]);

[L_pid,M_pid]=parallel(kp*Lr,Mr,kp*[1],[1]);

disp(`transmitancja regulatora PID')

tf(L_pid,M_pid)

% TRANSMITANCJA UKŁADU Z REGULATOREM PID

[L4,M4]=series(L_pid,M_pid,L1,M1);

[L_z_reg,M_z_reg]=cloop(L4,M4,-1);

subplot(4,1,3)

impulse(L_z_reg,M_z_reg)

[y2,x,t]=impulse(L_z_reg,M_z_reg,t);

grid

legend('uklad z regulatorem PID')

% POROWANIE

subplot(4,1,4)

plotyy(t,y1,t,y2)

title(`Porownanie odpowiedzi impulsowych')

xlabel(`t[s]')

grid

c) Układ regulatorem PID w programie SIMULINK

5. Wnioski

Program MATLAB jest pomocny przy tworzeniu układów automatyki (m. in. wyznaczaniu transmitancji operatorowej, modelowaniu, wyznaczaniu nastaw regulatora PID ), gdyż umożliwia dla raz podstawionych wartości, wyznaczać wykresy odpowiedzi układu na różne rodzaje sygnałów (skokowych, impulsowych), wyznaczenie charakterystyki Bode'a i charakterystyki Nyquist'a. Poprzez stworzenie modelu w programie SIMULINK można zasymulować działanie układu (wyznaczanie wykresów) , przy różnych rodzajach sygnałów wejściowych. Ułatwia on wykonywanie potrzebny operacji matematycznych (przy wyznaczaniu transmitancji operatorowej i wyznaczania nastaw regulatora PID), oraz zapewnia możliwość stworzenia odpowiednich wykresów w zależności od potrzeb.

---