Laboratorium Podstaw Automatyki
	Ćwiczenie nr 6 Analiza i synteza kombinacyjnych i sekwencyjnych układów logicznych
Data: Ocena	Wydział: Elektryczny Kierunek: Automatyka i Robotyka Rok studiów: II

Część teoretyczna.

Układy logiczne dzieli się na dwie grupy:

• układy kombinacyjne,

• układy sekwencyjne.

Układy kombinacyjne, nazywane również jednotaktowymi, są to układy dyskretne, których stan wyjść jest jednoznacznie określony stanami wejść, tzn. określonej kombinacji wejść odpowiada zawsze ta sama kombinacja wyjść.

Układy te nie zawierają elementów pamięci. Równanie odpowiadające strukturze takiego układu jest następujące:

gdzie: X - zbiór możliwych sygnałów wejściowych (x₁, x₂, ..., x_n), informujących o stanie obiektu regulacji,

Z - zbiór możliwych sygnałów wejściowych zewnętrznych (z₁, z₂, ..., z_l)

Y - zbiór możliwych sygnałów wyjściowych (y₁, y₂, ..., y_m)

Cyfrowe układy sekwencyjne (wielotaktowe) - sekwencyjny układ logiczny to taki, w którym sygnał wyjściowy zależy nie tylko od aktualnych, ale również od poprzednich wartości sygnałów wejściowych. Układy sekwencyjne są więc elementami pamiętającymi. Podstawowymi układami logicznymi sekwencyjnymi są przerzutniki. Najczęściej spotykane układy sekwencyjne to, poza przerzutnikami, układy czasowe, liczniki, rejestry i pamięci.

UK - układ kombinacyjny,

UP - układ pamięci.

Równania opisujące ten układ są następujące:

gdzie: X - zbiór wartości sygnałów wejściowych (x₁, x₂, ..., x_n) występujących w danej chwili

Y - zbiór wartości sygnałów wyjściowych (y₁, y₂, ..., y_m) --------------- | | ------------

Q - zbiór wartości sygnałów wyjściowych układu pamięci (Q₁, Q₂, ..., Q_k) ----| | -------

q - zbiór wartości sygnałów wejściowych układu pamięci (q₁, q₂, ..., q_t) -------| | -------

Najczęściej stosowaną metodą projektowania układów sekwencyjnych jest metoda tablic przejść i wyjść.

Przebieg ćwiczenia.

Zad. 1. Zadany kombinacyjny układ logiczny:

„1” - 0, 1, 4, 10, 14

„0” - 2, 3, 7, 8, 12, 13

Układ zminimalizowaliśmy metodą tablic Karnougha, a następnie zrealizowaliśmy praktycznie z wykorzystaniem bramek typu NAND.

Tablica Karnugha:

1	1	0	0
1	-	0	-
0	0	-	1
0	-	-	1

Na podstawie powyższej tablicy zapisaliśmy normalną postać minimalną sumy:

Aby zrealizować układ na elementach NAND, powyższą funkcję przedstawiliśmy w postaci iloczynów i negacji, aby wyeliminować operację sumowania:

Schemat układu logicznego ma następującą postać:

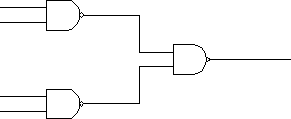
Po zmontowaniu układ działał prawidłowo.

Zad. 2. Zadany jest sekwencyjny układ logiczny o tablicy kolejności łączeń:

		0	1	2	3	4	5	6	7	8	9
2^0	X1	-	+				-
2^1	Y1	-				+		-
2^2	Y2	-			+				-
2^3	Y3	-		+						-
		0	1	9	13	15	14	12	8	4	0

Tablica jest realizowalna, ponieważ nie powtarzają się w niej stopnie łączenia.

Mając powyższe dane zapisaliśmy warunki działania układu w postaci tablic Karnougha:

0	0	-	0
0	-	-	0
0	0	1	1
0	0	-	0

0	0	-	-
0	-	-	1
0	1	1	1
0	0	-	-

0	-	-	0
1	-	-	1
1	1	1	1
-	-	-	-

Po dokonaniu minimalizacji tablic Karnogha otrzymaliśmy:

Schemat układu:

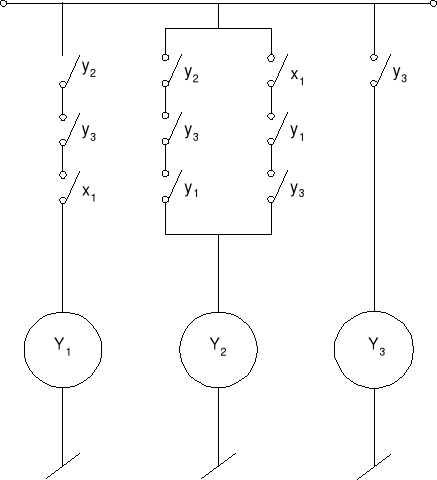
Wnioski.

W przypadku tego ćwiczenia należało sprawdzić czy układy wyliczone teoretycznie będą działały poprawnie po zmontowaniu praktycznym. W naszym przypadku układ z zadania pierwszego działał poprawnie, natomiast drugiego układu nie zdążyliśmy zmontować.

1

Laboratorium Podstaw Automatyki

________________________________________________________________________

___________________________________________________________________________

x₃x₄

x₁x₂

00

01

11

10

00

01

11

10

x₁

x₂

Cykl pracy

10

11

01

00

10

11

01

00

y₂y₃

x₁y₁

10

11

01

00

10

11

01

00

y₂y₃

x₁y₁

10

11

01

00

10

11

01

00

y₂y₃

x₁y₁

X

Y

Z

Układ

kombinacyjny

X

Y

UK

UP

q

Q