Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie modułu sztywności metodą dynamiczną. W tym celu należy wyznaczyć okres drgań wibratora dla kilku rozkładów mas.

Część teoretyczna

Twierdzenie Steinera:

Jeżeli znamy moment bezwładności I_o danego ciała względem pewnej osi przechodzącej przez środek masy tego ciała, to aby obliczyć moment bezwładności I względem dowolnej innej osi, równoległej do niej, należy do momentu bezwładności I_o dodać iloczyn masy ciała i kwadratu odległości d między tymi osiami.

I=I_o+md²

Twierdzenie Hooke'a:

Odkształcenie (wydłużenie lub skrócenie) jest wprost proporcjonalne do przyłożonej siły. Oznacza to, że jeżeli siła wzrasta wraz z nią wzrasta wydłużenie (skrucenie).

P=E ^Δl/_l

E- moduł, l-początkowa długość, Δl -wydłużenie

Własności sprężyste ciał stałych:

Odkształceniem nazywamy sprężystym gdy po usunięciu działającej siły odkształcenie znika. Jeżeli po usunięciu działającej siły odkształcenie nie znika, nazywamy je sprężystym lub trwałym.

Wzór na obliczenie modułu sztywności:

8πlI₁

r⁴(T₁²-T²)

l- długość drutu, T- okres drgań wibratora nie obciążonego lub obciążonego wstępnie,T₁- okres drgań wibratora obciążonego znanymi masami, r- promień drutu.

Rysunki do ćwiczenia

Jedną z metod wyznaczenia modułu sztywności jest metodę dynamiczna. W metodzie tej badany drut przymocowany jest górnym końcem do nieruchomego uchwytu, zaś na dolnym końcu przymocowany jest wibrator. Wibrator składa się z dwóch skrzyżowanych prętów zaopatrzonych w kołki umożliwiające nakładanie dodatkowych obciążeń.

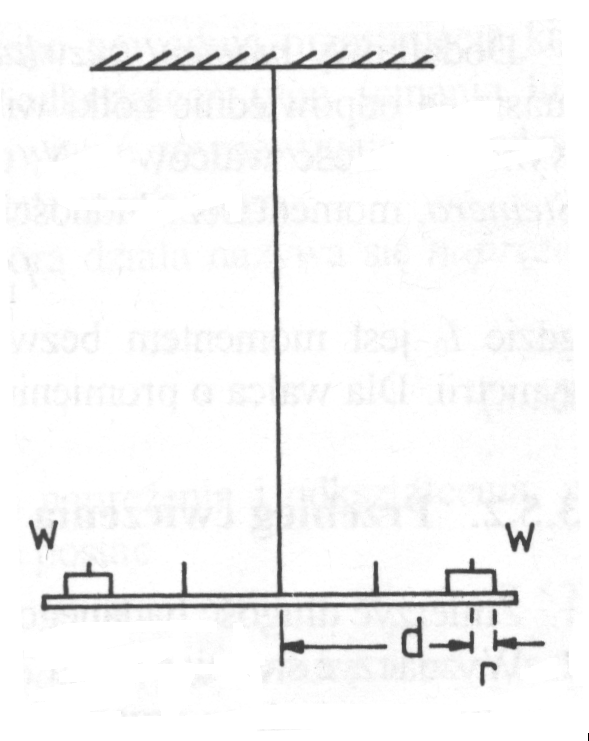
Urządzenie do wyznaczania modułu sztywności metodą dynamiczną

Dla małych walców w odległości d1

		Dla 2 obrotów
Lp.	wymiar	Pomiar 1	Pomiar 2	Wartość średnia
L	[m]	0,883	0,0885	0,884
2r	[m]	0,0008	0,0008	0,0008
T	[s]	0,94	0,9	0,92
2R	[m]	0,041	0,04	0,0405
M	[kg]	0,03561	0,03391	0,03476
D1	[m]	0,078	0,078	0,078
D2	[m]	0,078	0,178	0,173
T1	[s]	1,33	1,39	1,36
G	[Nm^2]	1,73*10^12	1,986*10^12	1,858*10^12

Błąd pośredni = 8,1*10¹⁰ Nm²

Dla małych walców w odległości d2

		Dla 2 obrotów
Lp.	wymiar	Pomiar 1	Pomiar 2	Wartość średnia
L	[m]	0,883	0,85	0,84
2r	[m]	0,0008	0,0008	0,0008
T	[s]	0,94	0,9	0,92
2R	[m]	0,041	0,04	0,0405
M	[kg]	0,03561	0,3391	0,3476
D1	[m]	0,078	0,078	0,078
D2	[m]	0,173	0,174	0,173
T1	[s]	0,158	0,157	0,1575
G	[Nm^2]	3,2*10^12	4,356*10^12	3,78*10^12

Błąd pośredni = 2,3*10¹⁰ Nm²

Dla dużych walców w odległości d1

		Dla 2 obrotów
Lp.	wymiar	Pomiar 1	Pomiar 2	Wartość średnia
L	[m]	0,883	0,885	0,884
2r	[m]	0,0008	0,0008	0,0008
T	[s]	0,94	0,9	0,92
2R	[m]	0,1	0,1	0,1
M	[kg]	0,212	0,212	0,212
D1	[m]	0,078	0,078	0,078
D2	[m]	0,173	0,174	0,173
T1	[s]	1,6	1,64	1,62
G	[Nm^2]	5,332*10^12	5,001*10^12	5,1665*10^12

Błąd pośredni = 1,4*10¹⁰ Nm²

Dla dużych walców w odległości d2

		Dla 2 obrotów
Lp.	wymiar	Pomiar 1	Pomiar 2	Wartość średnia
L	[m]	0,83	0,85	0,84
2r	[m]	0,0008	0,0008	0,0008
T	[s]	0,94	0,9	0,92
2R	[m]	0,1	0,1	0,1
M	[kg]	0,212	0,212	0,212
D1	[m]	0,078	0,078	0,078
D2	[m]	0,173	0,173	0,173
T1	[s]	1,0675	1,685	1,68
G	[Nm^2]	4,26*10^12	6,315*10^12	5,2875*10^12

Błąd pośredni = 3,5*10¹⁰ Nm²

Obliczenia:

3,14*0,041*0,01

4

m = ςv = ς m= 2700	Лd^2h
		4

= 0,03561 kg

I₀= ½ m R²= 0,5*0,356*(0,0205)²=7,123*10^-6 kg*m²

I₁= N I₀+Nmd²= 4*7,123*10^-6 + 4* 0,0339 *(0,078)²= 8,5348*10^-4 kg*m²

8πlI₁

r⁴(T₁²-T²)

8*3,14*0,935*8,5348*10^-4

(1,33^2- 0,92^2)

(0,0004)⁴

G=1,73*10¹²

I₀= ½ m R²=0,5*0,03391*(0,02)² = 6,78*10^-6 kg*m²

I₁= N I₀+Nmd²= 4*6,78*10^-6+4*0,3391*(0,078)²=8,7361*10^-4 kg*m²

Błędy pomiarowe:

∆l= 0,001 m

∆r=0,00005 m

∆R=0,001m

∆T= 0,01s

∆D= 0,001m

Wniosek:

Doświadczenie musi być obarczone bardzo dużym błędem gdyż do pomiaru użyliśmy stopera ręcznego co powoduje obarczenie pomiaru dużym błędem.

Błędy spowodowane są także dużymi zaokrągleniami występującymi kilka miejsc po przecinku. Można jednak stwierdzić, że uzyskane wyniki są do zaakceptowania.

2

---