POLITECHNIKA ŁÓDZKA

BOŻENNA KALUS-JĘCEK ZYGMUNT KUŚMIEREK

WZORCE WIELKOŚCI

ELEKTRYCZNYCH I OCENA

NIEPEWNOŚCI POMIARU

ŁÓDŹ 2000

SPIS TREŚCI

PRZEDMOWA ⁵

1. PODSTAWOWE WIADOMOŚCI O POMIARACH 1

1. Metrologia w nauce i technice 7

2. Istota pomiarów - pojęcia podstawowe 9

3. Organizacja państwowej służby miar 10

4. Układ jednostek miar 12

2. WZORCE JEDNOSTEK MIAR ²⁵

2.1. Wiadomości ogólne 25

1. Definicje 25

2. Hierarchia wzorców 26

2.2. Wzorce siły elektromotorycznej i napięcia 28

1. Ogniwo Westona 28

2. Źródła napięć wzorcowych wykorzystujące efekt Josephsona 32

3. Elektroniczne wzorce napięcia stałego 35

4. Kalibratory napięcia 40

2.3. Wzorce rezystancji 41

2.3.1.. Oporniki wzorcowe jednostopniowe 44

2. Oporniki w/.orcowe regulowane 47

3. Państwowy wzorzec oporu elektrycznego 48

2.4. Wzorce pojemności 49

2.5 Wzorce indukcyjności 53

1. Wzorce indukcyjności własnej 53

2. Wzorce indukcyjności wzajemnej 55

2.6. Źródła częstotliwości wzorcowych 55

3. METODY POMIAROWE 59

1. Ogólna charakterystyka metod 59

2. Metody analogowe i cyfrowe 59

1. Metody bezpośrednie i pośrednie 60

2. Metody porównawcze 60

4. ANALIZA BŁĘDÓW POMIAROWYCH 64

1. Przyczyny i rodzaje błędów 64

2. Teoria błędów 68

1. Błąd pomiaru bezpośredniego 68

2. Błąd pomiaru pośredniego 71

3. Błędy nadmierne i ich wykrywanie 76

5. NIEPEWNOŚCI WYNIKU POMIARU 80

1. Podstawy teorii niepewności 80

2. Prawo propagacji niepewności 84

3. Ocena niepewności w pomiarach bezpośrednich 86

1. Ocena niepewności typu A 86

2. Ocena niepewności typu B 89

3. Ocena niepewności typu A i B 91

5.4. Ocena niepewności w pomiarach pośrednich 94

1. Ocena niepewności typu A 94

2. Ocena niepewności typu B 98

3. Ocena niepewności typu A i B 102

5.5. Sposoby zapisu wyniku pomiaru 105

6. METODY REGRESJI 108

1. Wprowadzenie 108

2. Metoda graficzna 108

3. Metoda najmniejszych kwadratów 110

1. Regresja liniowa 110

2. Regresja wielomianowa ] 13

3. Regresja wielokrotna 114

LITERATURA 116

NORMY H7

PRZEDMOWA

W technice pomiarowej szczególną rolę odgrywają wzorce. Stanowią one podstawę dokładnych pomiarów różnych wielkości fizycznych. W skrypcie przedstawiono i omówiono wzorce podstawowych wielkości elektrycznych, ta­kich jak: wzorce siły elektromotorycznej, napięcia, oporu elektrycznego, pojem­ności, indukcyjności własnej i wzajemnej oraz częstotliwości. Z prezentowanych wzorców na szczególną uwagę zasługuje wzorzec napięcia zbudowany na bazie złącza Josephsona. Wzorzec ten umożliwia uzyskanie napięcia wzorcowego w przedziale od IV do 10V.

Jakość uzyskanego wyniku pomiaru można ocenić bazując na teorii niepew­ności lub teorii błędów. Teoria niepewności jest zalecaną do oceny jakości po­miaru przez międzynarodowe organizacje metrologiczne i europejskie laboratoria akredytowane. Powinna być stosowana wszędzie tam, gdzie wymagają tego prze­pisy. Obliczanie błędów czy niepewności jest procesem dość złożonym. Popraw­ne stosowanie teorii błędów i niepewności wymaga znajomości probabilisty­ki i statystyki matematycznej, a także dobrej znajomości samego zagadnienia pomiarowego. W niniejszym opracowaniu podano jedynie ogólne zasady wyzna­czania błędów i niepewności.

Skrypt przeznaczony jest dla studentów wydziałów elektrycznych i elektro­nicznych. Może być przydatny również dla studentów innych wydziałów.

Autorzy serdecznie dziękują Panu prof. dr hab. Zdzisławowi Nawrockiemu za wnikliwą recenzję skryptu i cenne uwagi.

l

PODSTAWOWE WIADOMOŚCI O POMIARACH

1.1. METROLOGIA W NAUCE I TECHNICE

Postęp nauki i techniki jest nierozerwalnie związany z rozwojem metrologii, reprezentującej wiedzę o miarach i mierzeniu. Szybki rozwój techniki pomiaro­wej wynika stąd, iż znajduje ona zastosowanie we wszystkich dziedzinach dzia­łalności człowieka, a więc w badaniach naukowych, wytwarzaniu dóbr material­nych, automatyzacji, komunikacji itd.

Nie ma takiej gałęzi nauk ścisłych lub stosowanych, w której nie zachodziłaby potrzeba wykonywania pomiarów. O jakimkolwiek zjawisku czy też wielkości można mówić, że jest znane dopiero wówczas, gdy umie się je określić nie tylko jakościowo lecz i ilościowo. Teoria, której nie można sprawdzić eksperymental­nie, może być jedynie hipotezą.

W szerszym ujęciu można powiedzieć, że metrologia ma do spełnienia trzy ściśle ze sobą związane grupy zadań:

• zadania naukowe,

• zadania urzędowo-prawne,

• zadania wynikające z udziału w procesach produkcji.
  Zadania naukowe metrologii obejmują następujące zagadnienia:

ustalenie podstawowych pojęć metrologicznych, terminologii

i symbolistyki,

opracowanie podstaw teorii mierzenia i zasad budowy przyrządów

i urządzeń pomiarowych,

opracowanie kryteriów oceny dokładności otrzymywanych wyników

pomiarów,

- prace nad jednostkami miar - doskonalenie układu jednostek,
realizację, ochronę i doskonalenie podstawowych wzorców wielkości
fizycznych,

opracowanie systemu przekazywania jednostek miar od wzorców podstawowych do narzędzi kontrolnych i użytkowych,

ustalenie dokładnych danych dla stałych fizycznych, chemicznych, astronomicznych, biologicznych i geofizycznych, udział w kształceniu kadr metrologów na wszystkich poziomach szkolnictwa. Zadania urzędowo-prawne metrologii to:

zabezpieczenie jednolitości miar w nauce, technice i gospodarce na­rodowej,

wprowadzenie legalnego układu jednostek i przestrzeganiu jego sto­sowania,

ustalenie obowiązujących wymagań dotyczących przyrządów i urzą­dzeń pomiarowych,

ustalenie wymagań dotyczących laboratoriów pomiarowych, przeprowadzanie badań prototypów przyrządów i urządzeń pomiaro­wych,

dokonywanie urzędowego uwierzytelniania kontrolnych wzorców miar i kontrolnych przyrządów pomiarowych, kontrola jakości produkowanych narzędzi pomiarowych, sprawowanie nadzoru nad służbą miar.

Zadania metrologii wynikające z jej udziału w procesach produkcji przemy­słowej, to:

ustalenie dokładnych danych dotyczących właściwości technicznych surowców i materiałów produkcyjnych, wprowadzanie metod racjonalnego projektowania wyrobów, wprowadzanie technicznie i ekonomicznie uzasadnionych procesów technologicznych,

opracowanie zadań i struktury organizacyjnej nowoczesnej kontroli jakości,

organizowanie służby miar w zakładach przemysłowych i placówkach badawczych.

Odpowiedni poziom i stały rozwój metrologii jest nieodzownym warunkiem unowocześniania produkcji i wzrostu jakości wyrobów. Wymagania stawiane technice pomiarowej stale wzrastają. Mierzy się coraz więcej wielkości o szero­kim zakresie mierzalnych wartości. Mierzone są wielkości o dużej zmienności w czasie. Stosowane przyrządy pomiarowe powinny charakteryzować się dobrymi właściwościami dynamicznymi, dużą czułością i niezawodnością.

Dążenie do centralizacji pomiaru, pozwalającej z pewnej odległości od obiektu kontrolować i regulować proces technologiczny, implikuje rozwój auto­matyzacji pomiarów oraz przyrządów rejestrujących. Budowane są całe systemy pomiarowe, pomiarowo-diagnostyczne itp. Dąży się do uzyskania informacji o coraz większej dokładności, uznając przy tym niemożność dokonania pomiaru

bezbłędnego. Powstaje konieczność określania dopuszczalnych granic błędów i uzależnienia ich od wartości i od konkretnego celu, dla którego prowadzi się po­miar. Udział kosztów aparatury pomiarowej w kosztach inwestycyjnych sięga kilku do kilkunastu procent i ma tendencję rosnącą.

Rozwój technologii wytwarzania aparatury pomiarowej spowodował zmianę treści metrologii. Przestają być problemem: technika odczytu, rola obserwatora, dobór czułości czy zakresu pomiarowego, dobór rezystancji wewnętrznej i inne zagadnienia, które dominowały w metrologii klasycznej. Zamiast tych proble­mów powstają nowe jak np.: eliminacja zakłóceń, odpowiednie zaplanowanie eksperymentu, oprogramowanie systemu itd.

1.2. ISTOTA POMIARU - POJĘCIA PODSTAWOWE.

Pomiar jest zbiorem operacji mających na celu określenie wartości wielkości mierzonej. Według metrologii stosowanej definicja pomiaru jest następująca:

Pomiar jest to zespól czynności poznawczych, których celem jest dostarczenie danych do ilościowego opisu przedmiotów lub zjawisk, polegający na porówna­niu, drogą doświadczenia fizycznego z określoną dokładnością, wielkości mierzo­nej z pewną jej wartością obraną za jednostkę.

W wyniku pomiaru następuje przyporządkowanie badanym cechom przed­miotów lub zjawisk pewnej miary liczbowej, wyrażającej stosunek wielkości mierzonej do jej jednostki. Stosunek ten jest nazywany wartością wielkości mie­rzonej. Definicje pojęć występujących w definicji pomiaru są następujące:

Wartość wielkości mierzonej jest to liczba wyrażająca stosunek wielkości mierzonej do jej jednostki.

Wielkość mierzona (metrologiczna), mezurand jest to cecha zjawiska, dala lub substancji, rozróżnialna jakościowo i możliwa do określenia ilościowo.

Jednostka miary jest to umownie przyjęta wartość danej wielkości, służąca do porównywania ze sobą innych wartości tej samej wielkości.

Pomiar określa stan badanej wielkości w pewnej chwili czasowej i w określo­nych warunkach zewnętrznych.

10

Z matematycznego punktu widzenia można zauważyć, że w pomiarze biorą udział dwa zbiory wielkości:

zbiór X - wielkości x oraz zbiór W- znanej wielkości w.

Elementy zbioru- W są uporządkowane według wartości i oznaczone wskaźnikiem i. Jest to zbiór skończony, utworzony przez wielkość wzorcową, odtwarzaną w procesie pomiaru przez przyrząd pomiarowy. Kolejne elementy tego zbioru w/ i w/+/ różnią się między sobą o wartość 2e > 0. Czyli

w,.-H>.₊₁=2e>0

Wielkość mierzona stanowi skończony lub nieskończony zbiór ograniczony od góry i od dołu. Na tej podstawie, pomiarem można nazwać takie czynności, które podporządkowują elementowi x ze zbioru X element w ze zbioru W. Po­nieważ zbiór W jest dyskretny, podporządkowanie nie może być jednoznaczne; wynikiem podporządkowania pomiaru jest nierówność

_Wi<x< w_m

Mogą istnieć zbiory W tej samej wielkości o różnych wartościach 2e,>0 od­twarzane przez przyrządy pomiarowe o różnych właściwościach metrologicz­nych. Nie istnieje jednak zbiór, dla którego e,=0. Założenie 2ep>0 jest podstawo­wym założeniem metrologii.

Niedoskonałość zmysłów obserwatora nie pozwala odróżnić dwóch sąsiednich elementów zbioru W o różnicy mniejszej niż próg czułości równy 2e₍. Ten próg jest ograniczony kwantowością wielu zjawisk.

1.3. ORGANIZACJA PAŃSTWOWEJ SŁUŻBY MIAR

Podstawą organizacji służby miar w Polsce są przepisy zawarte w usta­wie z dnia 3 kwietnia 1993 r. „Prawo o miarach" (Dziennik Ustaw nr 55, poz.248). Zgodnie z tą ustawą sprawami miar i probiernictwa zajmuje się Główny Urząd Miar (GUM) z siedzibą w Warszawie. Organizację GUM określa statut nadany przez prezesa Rady Ministrów. Na czele Głównego Urzędu Miar stoi pre­zes, który jest powoływany przez premiera Rzeczpospolitej Polskiej. Prezesowi GUM podlegają dyrektorzy Okręgowych Urzędów Miar, a dyrektorom tym - na­czelnicy Obwodowych Urzędów Miar. Okręgowe Urzędy Miar znajdują się w: Bydgoszczy, Gdańsku, Katowicach, Krakowie, Łodzi, Szczecinie i Warszawie.

Główny zakres działań prezesa GUM to:

11

1. wydawanie przepisów metrologicznych określających wymagania,
   jakim podlegają przyrządy pomiarowe, warunki właściwego ich sto­
   sowania oraz okresy ważności dowodów kontroli;

2. określanie metod sprawdzania zgodności właściwości przyrządów
   pomiarowych z wymaganiami przepisów.

Ustawa „Prawo o miarach" określa system miar w Polsce oraz zasady jego stosowania. Naczelną jego zasadą jest współpraca organów administracji miar zapewniająca zgodność i wymaganą dokładność wyników pomiarów dokonywa­nych w kraju oraz ich powiązanie z międzynarodowym systemem miar.

Ustawa „Prawo o miarach określa legalne jednostki miar, którymi są jednostki Międzynarodowego Układu Jednostek Miar (SI) oraz jednostki nie należące do układu SI, lecz dopuszczone do stosowania w drodze rozporządzenia Rady Mini­strów.

Najistotniejszą częścią prawa o miarach jest kontrola metrologiczna przyrzą­dów pomiarowych.

Przyrządami pomiarowymi są urządzenia techniczne przeznaczone do wyko­nywania pomiarów lub odtworzenia wartości danej wielkości.

Według art.9 ustawy „Prawo o miarach" przyrządy pomiarowe podlegają kontroli metrologicznej organów administracji miar w formie:

1. legalizacji;

2. uwierzytelnienia;

3. zatwierdzenia typu.

Legalizacja jest sprawdzeniem, stwierdzeniem i poświadczeniem przez organ administracji miar (GUM, Okręgowy lub Obwodowy UM), że przyrząd spełnia wymagania przepisów metrologicznych. Dowodem legalizacji jest cecha legali­zacyjna umieszczona na przyrządzie lub świadectwo legalizacyjne. Przyrządy pomiarowe powinny być zgłaszane do legalizacji pierwotnej przez wytwórcę, sprzedawcę lub importera przed wprowadzeniem ich do obrotu lub użytkowania. Obowiązek zgłaszania do legalizacji ponownej ciąży na użytkowniku.

Uwierzytelnienie jest sprawdzeniem, stwierdzeniem i poświadczeniem, że przyrząd pomiarowy spełnia wymagania metrologiczne ustalone w przepisach, normach, zaleceniach międzynarodowych lub właściwych dokumentach, a jego wskazania zostały odniesione do państwowych wzorców jednostek miar. Obowiązkowi uwierzytelnienia podlegają przyrządy pomiarowe określone przez prezesa GUM, mające znaczenie dla bezpieczeństwa życia, ochrony zdrowia i środowiska.

Dowodem uwierzytelnienia jest świadectwo albo cecha uwierzytelnienia. Prezes GUM określa okres ważności uwierzytelnienia.

Przyrządy pomiarowe zalegalizowane uważa się za odpowiadające uwierzytel­nieniu.

12

Przyrządy pomiarowe podlegające legalizacji lub uwierzytelnieniu, a także inne przyrządy pomiarowe określone przez prezesa GUM, podlegają zatwierdze­niu typu. Przez typ przyrządu pomiarowego rozumie się ostateczną realizację -w wykonaniu określonego wytwórcy - przyrządu pomiarowego, którego wszyst­kie elementy mające wpływ na właściwości metrologiczne zostały określone w dokumentacji. Decyzje zatwierdzenia typu są podejmowane na podstawie ba­dań prototypów lub egzemplarzy produkcyjnych tych przyrządów sprawdzają­cych zgodność z wymaganiami zawartymi w przepisach metrologicznych, nor­mach, zaleceniach międzynarodowych lub innych właściwych dokumentach. Wykonanie tych badań GUM morze powierzyć Okręgowym lub Obwodowym UM. Przyrządom, które uzyskały zatwierdzenie typu prezes GUM może nadać znak typu. Znak typu składa się z dużych liter RP i T, dwóch ostatnich cyfr roku, w którym nadano typ przyrządu pomiarowego i kolejnego numeru znaku. (Np. RP T 97 5, gdzie 97 - są dwiema cyframi roku 1997, a 5 jest kolejnym numerem nadanego znaku typu).

Większość przyrządów pomiarowych nie podlega legalizacji ani obowiąz­kowi uwierzytelnienia lecz prawie wszystkie przyrządy pomiarowe podlegają obowiązkowi zatwierdzenia typu.

1.4. UKŁAD JEDNOSTEK MIAR

W przyrodzie występuje bardzo duża liczba wielkości mierzalnych. Wielko­ści te są ze sobą powiązane równaniami i definicjami wynikającymi z praw przy­rody. Dlatego definiowanie jednostek dla poszczególnych wielkości bez powią­zania z pozostałymi wielkościami byłoby nieracjonalne. Tworzy się układy jed­nostek, w których jednostki miar wszystkich wielkości powinny być jednoznacz­ne oraz łatwo odtwarzalne.

W procesie tworzenia układu jednostek tworzy się zbiór wszystkich wielko­ści występujących w tych dziedzinach wiedzy, do których będzie stosowany układ.

Zbiór wszystkich wielkości występujących w równaniach danej dziedziny wiedzy nazywa się układem wielkości.

Spośród wielkości należących do układu wyróżnia się kilka wielkości, które umownie przyjmuje się za wielkości podstawowe.

Każda wielkość podstawowa winna spełniać dwa warunki:

• W definicji wielkości podstawowej nie mogą występować pozostałe wielkości podstawowe.

13

• Wraz z pozostałymi wielkościami podstawowymi układu pozwala zdefi­niować wszystkie wielkości danego układu wielkości. Z różnych przyczyn pierwszy warunek nie zawsze bywa spełniony.

Wielkość pochodna jest to wielkość określona za pomocą wielkości podsta­wowych.

Wielkościom układu przypisuje się jednostki miary; przy tym, jednostki przypisane wielkościom podstawowym nazywa się jednostkami podstawowymi, a jednostki miar wielkości pochodnych odpowiednio - jednostkami pochodnymi

Uporządkowany zbiór jednostek miar określonego układu wielkości stanowi układ jednostek miar.

Dla jednego układu wielkości można utworzyć kilka układów jednostek po­nieważ w pewnym stopniu dobór jednostek jest dowolny (np.: układy CGS i MKS z różnymi modyfikacjami). Obecnie w większości krajów świata, w tym również i w Polsce obowiązuje Międzynarodowy Układ Jednostek Miar Sl (Systeme International d'Unites) w skrócie SI. Układ SI został zatwierdzony przez XI Generalną Konferencję Miar w 1960r. Układ ten był kilkakrotnie mody­fikowany i uzupełniany uchwałami kolejnych Generalnych Konferencji Miar (XII - 1964r., XIII - 1967/68r., XIV - 1971r., XV - 1975r. i XVI - 1979r.).

W układzie SI wyróżniono siedem wielkości i jednostek podstawowych oraz dwie wielkości i jednostki uzupełniające.

Lp.	Wielkość	Jednostka	Symbol
1.	długość	metr	m
2.	masa	kilogram	kg
3.	czas	sekunda	s
4.	natężenie prądu elektrycznego	amper	A
5.	temperatura	kelwin	K
6.	światłość	kandela	cd
7.	ilość materii	mol	mol
8.	kąt płaski	radian	rad
9.	kąt bryłowy	steradian	sr

W układzie SI przenikalność dielektryczna próżni e₀ i przenikalność ma­gnetyczna próżni Ho są liczbami mianowanymi; ich wartości i wymiar są nastę­pujące

—10-⁹-,

36n m

= 47i.l(T⁷-m

(1.1)

14

Są one związane z prędkością światła w próżni zależnością

T

(1.2)

Niektóre z jednostek podstawowych układu SI były stosowane już we wcze­śniej używanych układach jednostek miar, jednak wraz z rozwojem nauki i tech­niki pomiarowej zmieniały się ich definicje. Obecnie dąży się do definiowania jednostek podstawowych przy wykorzystaniu zjawisk atomowych, co zapewnia dużą dokładność i powtarzalność wzorców „zbudowanych" według takich defini­cji.

Jednostka długości - metr występowała w wielu wcześniejszych układach jednostek miar. Metr definiowano początkowo w odniesieniu do długości połu­dnika ziemskiego, później - według platynoirydowego wzorca z Międzynarodo­wego Biura Miar i Wag w Sevres. Do 1983 roku metr był odwzorowywany przez porównanie z długością fali świetlnej, pomarańczowej linii widma izotopu kryp­tonu 36⁸⁶Kr. Obecnie metr jest definiowany na podstawie prędkości światła w próżni. Obowiązuje poniższa definicja.

Metr jest to długość drogi przebytej w próżni przez światło w czasie równym

l _s

299792458 '

Obowiązująca definicja metra nie spełnia jednego z warunków stawianych wielkościom podstawowym układu jednostek lecz jej przyjęcie zapewnia lepszą dokładność odtworzenia jednostki, co ma związek z rozwojem pomiarów prędko­ści światła w próżni.

Kilogram -jednostka masy nie doczekał się dotychczas wzorca atomowego, jakkolwiek istnieje propozycja wykorzystania do tego celu izotopu węgla ^I2C (jako masę 50259,36217-10²¹ atomów tego izotopu). Nadal obowiązuje więc kla­syczna definicja.

Kilogram jest masą międzynarodowego wzorca tej jednostki, przecho­wywanego w Międzynarodowym Biurze Miar i Wag pod Paryżem. Jednostka czasu - sekunda początkowo była definiowana w odniesieniu do średniej doby słonecznej, później zaś w odniesieniu do czasu trwania roku zwrot­nikowego. Zgodnie z tendencją do wykorzystywania zjawisk atomowych obecnie sekundę odwzorowuje się za pomocą tak zwanego „wzorca cezowego", a defini­cja sekundy jest następująca.

Sekundajest czasem trwania 9 192 631 770 okresów promieniowania odpowiadającego przejściu między dwoma poziomami nadsubtelnymi stanu podstawowego atomu ^l33Cs (cezu 133).

15

Jednostka natężenia prądu - amper jest definiowana w oparciu o prawo Ampe-re'a dotyczące wzajemnego oddziaływania dwóch przewodów wiodących prąd. Amper Jest natężeniem prądu elektrycznego, nie ulegającego żadnym zmia­nom, który - pfynąc w dwóch przewodach równoległych, prostoliniowych, nieskończenie długich, o przekroju kołowym znikomo małym, umieszczonych w próżni w odległości Im od siebie - wytwarza miedzy tymi przewodami silę 2-10~⁷Nna każdy metr długości przewodu.

Praktyczna realizacja tak zdefiniowanego wzorca jest niemożliwa. Do od­wzorowania wzorca ampera wykorzystuje się tzw. „wagą prądową", w której do wytworzenia siły powodującej wychylenie belki wagi wykorzystuje się wzajemne oddziaływanie dwu połączonych szeregowo cewek (ruchomej i nieruchomej), przez które płynie prąd.

Jednostka temperatury - kelwin - jest definiowany jako jednostka termody­namicznej (rozpoczynającej się od zera bezwzględnego) skali temperatur.

Kelwin jest częścią temperatury termodynamicznej punktu potrój-

273,16

nego wody.

Punkt potrójny wody oznacza stan wody przy takich ciśnieniu i temperatu­rze, że występuje ona w trzech stanach: stałym, ciekłym i gazowym. Ten przypa­dek zachodzi przy temperaturze równej 273,16 K (0,01°C) i ciśnieniu równym 631,163N/m².

Ponieważ kelwin jest równy stosowanemu dotąd stopniowi Celsjusza, do­puszczalne jest przejściowo stosownie skali Celsjusza.

Tę samą nazwę i oznaczenie stosuje się do wyrażania stanu temperatury jak i róż­nicy temperatury.

Jednostka światłości - kandela -do niedawna była realizowana za pomocą wzorca zbudowanego w oparciu o teoretyczne pojęcie „ciała doskonale czarne­go", które całkowicie pochłania padające nań promieniowanie, zaś jako źródło promieniuje najintensywniej ze wszystkich ciał fizycznych. Obecna definicja kandeli jest następująca.

Kandela jest światłością, którą ma w określonym kierunku źródło emitujące promieniowanie monochromatyczne o częstotliwości 540-10^I2Hz i którego

natężenie promieniowania jest równe W/sr.

Mol jako podstawowa jednostka układu SI, służąca do określenia ilości mate­rii, został wprowadzony dopiero w 1971 roku, zaś jego definicja jest następująca.

16

Mol jest to liczność materii występująca, gdy liczba cząstek lub atomów jest równa liczbie atomów zawartych w masie 0,012kg czystego nuklidu węgla ^I2C.

Radian i steradian są jednostkami uzupełniającymi, zaś ich definicje są znane z geometrii.

Radian jest kątem płaskim o wierzchołku w środku koła, wycinającym z ob­wodu tego koła łuk o długości równej jego promieniowi. Steradian jest kątem bryłowym o wierzchołku w środku kuli, wycinają­cym z powierzchni tej kuli pole równe kwadratowi jej promienia. Za pomocą jednostek podstawowych i uzupełniających definiuje się. jednost­ki miar wszystkich wielkości pochodnych. Będą to tzw. jednostki pochodne. De­finicje jednostek pochodnych nie mają urzędowych sformułowań słownych. Są one formułowane indywidualnie na podstawie równań definicyjnych określają­cych związek między daną wielkością pochodną a wielkościami podstawowymi. Wykaz ważniejszych jednostek miar układu SI zestawiono w tabeli 1.1.

Międzynarodowy Układ Jednostek Miar jest układem uniwersalnym i spój­nym.

Uniwersalność układu oznacza, że może on być stosowany zarówno we wszystkich dziedzinach nauki, jak i w technice. Jest to cecha pozwalająca wyeli­minować bałagan i trudność współpracy, wynikające ze stosowania różnych układów jednostek miar, różnych nazw jednostek, różnych ich wymiarów i róż­nych oznaczeń. Koherentność układu, czyli spójność jednostek miar, oznacza, że wszystkie należące do układu główne jednostki miar mają w równaniach defini­cyjnych współczynnik liczbowy równy jedności (zob. Tabela 1.1). W innych .wcześniej stosowanych układach jednostek miar wartości tych współczynników liczbowych bywały różne. Spójność układu SI jest bardzo korzystna, upraszcza bowiem dokonywanie wszelkich obliczeń. W układzie SI określona wielkość ma jedną jednostkę miary, jedną nazwę tej jednostki, jeden symbol i jeden wymiar jednostki.

Wykaz ważniejszych jednostek miar w układzie SI

Tabela 1.1

L.p.	Wielkość	Nazwa jednostki miary	Ozna­czenie jed­nostki	Definicje i relacje między jednostkami	Wymiar w jed­nostkach podsta­wowych	Uwagi
1	2	3	4	5	6	7
1	Długość	metr	m	Metr jest to długość równa drodze, jaką przebywa świa­tło w czasie równym 1/299792458 sekundy
2	Masa	kilogram	kg	Kilogram jest to masa międzynarodowego wzorca tej jednostki przechowywanego w Międzynarodowym Biu­rze Miar w Sevres.
3	Czas	sekunda	s	Sekunda jest to czas równy 9192631770 okresów pro­mieniowania odpowiadającego przejściu między dwoma nadsubtemymi poziomami stanu podstawowego atomu ^I33Cs (cezu!33).
4	Natężenie prądu elek­trycznego	amper	A	Amper jest to prąd elektryczny nie zmieniający się, któ­ry płynąc w dwóch równoległych prostoliniowych, nie­skończenie długich przewodach o przekroju znikomo małym, umieszczonych w próżni w odległości Im (metr) od siebie - wywołałby między tymi przewodami siłę 2-10"^7N (niuton) na każdy metr długości.		Stosuje się również nazwę: prąd elektrycz­ny
5	Temperatu­ra	kelwin	K	Kelwin jest to 1/273,16 temperatury termodynamicznej punktu potrójnego wody.		Dopuszcza się °C
6	Liczność materii	mol	mol	Mol jest to liczność materii występująca, gdy liczba cząstek jest równa liczbie atomów zawartych w masie 0,012 kg (kilogram) ^12C (węgla 12).		Stosowana jest również nazwa: ilość materii

Tabela 1.1 cd

1	2	3	4	5	6	7
7	Światłość	kandela	cd	Kandela jest światłością, którą ma w określonym kie­runku źródło emitujące promieniowanie monochroma­tyczne o częstotliwości 540-10^12Hz i którego natężenie promieniowania jest równe 1/683 W/sr
8	Kąt płaski	radian	rad	Radian jest to kąt płaski, zawarty między dwoma pro­mieniami koła, wycinającym z jego okręgu łuk o długo­ści równej promieniowi tego koła.
9	Kąt bryło­wy	steradian	sr	Steradian jest to kąt bryłowy o wierzchołku w środku kuli, wycinający z jej powierzchni część równą po­wierzchni kwadratu o boku równym promieniowi tej kuli.
10	Pole powierzchni	metr kwadratowy	m^2	Metr kwadratowy jest to powierzchnia równa po­wierzchni kwadratu, którego bok ma długość Im (metr)	Im^2
11	Objętość	metr sześcienny	m^3	Metr sześcienny jest to objętość równa objętości sze­ścianu, którego krawędź ma długość Im (metr)	Im^3
12	Częstotli­wość	herc	Hz	Herc jest to częstotliwość zjawiska okresowego, którego okres jest równy Is (sekunda).	Is'^1
13	Prędkość liniowa	metr na sekundę	m/s	Metr na sekundę jest to prędkość liniowa, z jaką poru­szający się punkt przebywa drogę o długości Im (metr) w czasie Is (sekunda)	Im-s'^1
14	Prędkość kątowa	radian na sekundę	rad/s	Radian na sekundę jest to prędkość kątowa, z jaką poru­szający się po okręgu koła punkt zakreśla łuk odpowia­dający Irad (radian) w czasie Is (sekunda).	ls-'-rad
15	Przyspie­szenie liniowe	metr na kwadrat sekundy	m/s^2	Metr na kwadrat sekundy jest to przyspieszenie liniowe, przy którym prędkość liniowa zmienia się o Im/s (metr na sekundę) w czasie Is (sekunda)	Im-s'^2

Tabela 1.1 cd

1	2	3	4	5	6	7
16	Przyspie­szenie kątowe	radian na kwadrat sekundy	rad/s^2	Radian na kwadrat sekundy jest to przyspieszenie kąto­we, przy którym prędkość kątowa zmienia się o 1 rad/s (radian na sekundę) w czasie Is (sekunda).	ls-^2-rad
17	Gęstość (masy)	kilogram na metr sześcienny	kg/m^j	Kilogram na metr sześcienny jest to gęstość ciała mają­cego masę Ikg (kilogram) i objętość Im^3 (metr sze­ścienny).	lm-^3-kg
18	Pęd	kilogram o-metr na sekundę	kg-m/s	Kilogramometr na sekundę jest to pęd ciała o masie Ikg (kilogram) poruszającego się z prędkością Im/s ( metr na sekund e).	Im-kg-s"'
19	Siła	niuton	N	Niuton jest to siła, która w kierunku jej działania nadaje masie Ikg (kilogram) przyspieszenie Im/s^2	lm-kg-s"^2
20	Moment siły	niutonometr	N-m	Niutonometr jest to moment siły IN (niuton) względem punktu położonego w odległości Im (metr) od kierunku działania tej siły.	Im^2-kg-s-^2
21	Ciśnienie	paskal	Pa	Paskal jest to ciśnienie występujące na powierzchni pła­skiej Im^2 ( metr kwadratowy), na którą działa prostopa­dle siła IN (niuton).	lm-'-kg-s-^2	N/m^2
22	Energia, praca	dżul	J	Dżul jest to energia równa pracy wykonanej przez siłę IN (niuton) w kierunku jej działania, na drodze o długo­ści Im {metr).	Im^2-kg-s-^2	N-m
23	Moc	wat	W	Wat jest to moc, przy której praca U (dżul) wykonana jest w czasie Is (sekunda).	Im^2-kg-s-^3	J/s
24	Gęstość mocy	wat na metr kwadratowy	W/m^2	Wat na metr kwadratowy jest to gęstość mocy wystę­pująca, gdy moc 1W (wat) przypada na powierzchnię Im^2 (metr kwadratowy).	Ikg-s'^3

Tabela 1.1 cd

1	2	3	4	5	6	7
25	Gęstość prądu elektrycz­nego	amper na metr kwadratowy	A/m^2	Amper na metr kwadratowy jest to gęstość prądu elek­trycznego występująca, gdy prąd 1A (amper) rozkłada się równomiernie na powierzchni Im^2 (metr kwadrato­wy), prostopadłej do kierunku tej gęstości elektrycznej.	lm'^2-A
26	Ładunek elektryczny	kulomb	C	Kulomb jest to ładunek elektryczny przepływający w czasie Is (sekunda) przez powierzchnię, gdy prąd elektryczny płynący przez tę powierzchnię wynosi 1A (amper).	ls-A
27	Napięcie elektryczne, różnica po­tencjałów, siła elektro­motoryczna	wolt	V	Wolt jest to napięcie elektryczne występujące między dwiema powierzchniami ekwipotencjalnymi jednorod­nego przewodu prostoliniowego, w którym płynie nie zmieniający się prąd 1A (amper), a moc między tymi powierzchniami jest równa 1 W (wat).	lm^z-kg-s'^3-A°	W/A
28	Natężenie pola elek­trycznego	wolt na metr	V/m	Wolt na metr jest to natężenie równomiernego pola elektrycznego, w którym różnica potencjałów między dwiema płaszczyznami ekwipotencjalnymi odległymi od siebie o Im (metr) wynosi IV (wolt).	Im-kg-s'^3- A'^1
29	Indukcja elektryczna	kulomb na metr kwa­dratowy	C/m^2	Kulomb na metr kwadratowy jest to indukcja elektrycz­na, przy której na powierzchni przewodnika równej Im^2( metr kwadratowy), prostopadłej do linii pola elek­trycznego, indukuje się ładunek elektryczny 1C (ku­lomb).	lnT^2-s-A
30	Pojemność elektryczna	farad	F	Farad jest to pojemność elektryczna, jaką ma konden­sator, w którym między elektrodami występuje napięcie elektryczne IV (wolt), gdy znajdują się na nich różno-imienne ładunki o wartości 1C (kulomb) każdy.	lm-^2.kg-'s^4-A^2	C/V

to

o

Tabela 1.1 cd

1	2	3	4	5	6	7
,^31	Przenikal-ność die­lektryczna	Paradna metr	F/m	Parad na metr jest to przenikalność dielektryczna (bez­względna) środowiska izotropowego, w którym polu elektrycznemu odpowiada indukcja elektryczna IC/m^2(kulomb na metr kwadratowy).	Im^-kg-tf-A^2
32	Opór elek­tryczny, (rezystan­cja, reak-tancja, im-pedancja)	om	n	Om jest to opór elektryczny między dwiema powierzch­niami ekwipotencjalnymi przewodu jednorodnego pro­stoliniowego, gdy niezmienne napięcie elektryczne IV (wolt) występujące między tymi powierzchniami wy­wołuje w tym przewodzie prąd elektryczny 1 A (amper).	lm^2-kg-s-^3-A'^2	V/A
33	Rezystyw-ność, opór elektryczny właściwy	omometr	n-m	Omometr jest to rezystywność jednorodnego przewod­nika, gdy wykonany z niego przewód o przekroju po­przecznym Im^2 ( metr kwadratowy) i długości Im (metr) ma opór elektryczny 1Q (om)	Im^3-kg- s'^3 -A'^2
34	Przewod­ność elek­tryczna	simens	s	Simens jest to przewodność elektryczna przewodu o oporze Ifł (om).	Im-^g-^-A^2	i/n
35	Konduk-tywność	simens na metr	S/m	Simens na metr jest to konduktywność przewodnika jednorodnego o rezystywności Iftm ( omometr)	lm-^3-kg-'s^3-A^2	l/ttm
36	Strumień magnetycz­ny	weber	Wb	Weber jest to strumień magnetyczny, który malejąc jed­nostajnie do zera w czasie Is (sekunda) indukuje siłę elektromotorycznąlY (wolt) w obejmującym ten stru­mień magnetyczny obwodzie zamkniętym jednozwojo-wym wykonanym z przewodu o przekroju kołowym znikomo małym.	lm^2-kg-s°-A^-1	V-s

K> K)

Tabela 1.1 cd

1	2	3	4	5	6	7
37	Indukcja magnetycz­na	tesla	T	Tesla jest to indukcja magnetyczna pola magnetycznego równomiernego, przy której na przekrój poprzeczny Im^2 (metr kwadratowy) przypada strumień magnetycz­ny lWb(weber).	lkg-s-^2.A-'	Wb/m^210^4Gs
38	Natężenie pola ma­gnetyczne­go	amperna metr	A/m	Amper na metr jest to natężenie pola magnetycznego, jakie występuje na powierzchni bocznej walca kołowe­go o obwodzie Im (metr), stycznie do powierzchni bocznej tego walca i prostopadle do jego tworzącej, gdy przez znajdujący się w osi tego walca przewód prostoli­niowy nieskończenie długi o przekroju znikomo małym płynie nie zmieniający się prąd 1 A (amper).	lm-'-A
39	Indukcyj-ność	henr	H	Henr jest to indukcyjność obwodu, w którym indukuje się siła elektromotoryczna IV (wolt), gdy prąd elek­tryczny płynący w tym obwodzie zmienia się jednostaj­nie o 1 A (amper) w czasie Is (sekunda).	lm^z-kg-s-^2-A-^2	Vs/A
40	Przenikal-ność ma­gnetyczna	henr na metr	H/m	Henr na metr jest to przenikalność magnetyczna (bez­względna) środowiska izotropowego, w którym polu magnetycznemu lA/m (amper na metr) odpowiada in­dukcja magnetyczna 1T (tesla).	Ira-kg- s'^2-A-^2	Tm/A
41	Siła ma-gnetomoto-ryczna	amper	A	Amper jest to siła magnetomotoryczna występująca wzdłuż dowolnej krzywej zamkniętej stanowiącej brzeg powierzchni, gdy przez tę powierzchnię przenika jeden przewód z nie zmieniającym się prądem 1 A (amper).	1A

Tabela 1.1 cd

1	2	3	4	5	6	' 7
42	Strumień świetlny	lumen	Im	Lumen jest to strumień świetlny wysyłany w kącie bry­łowym Isr (steradian) przez punktowe źródło światła o światłości Icd (kandela)	lcd-sr
43	Natężenie oświetlenia	luks	lx	Luks jest to natężenie oświetlenia wytworzone przez strumień świetlny llm (lumen) na powierzchni Im^2(metr kwadratowy).	lm"^2-cd-sr	Im/m^2
44	Luminancja	kandela na metr kwa­dratowy	cd/m^2	Kandela na metr kwadratowy jest to luminancja po­wierzchni Im^2 (metr kwadratowy), której światłość w kierunku prostopadłym do tej powierzchni jest równa Icd (kandela).	lm"^2-cd

24

Jeśli jednostki główne są zbyt duże lub zbyt małe do określenia w prosty spo­sób jakiejś wielkości, stosuje się dziesiętne wielokrotności lub podwielokrotności tych jednostek. Są one zapisywane za pomocą przedrostków przed nazwą jed­nostki (por. Tabela 1.2).

Przedrostki oznaczające krotność jednostek miar Tabela 1.2

Przedrostek	Oznaczenie	Krotność
eksa	E	10^18
peta	P	10^15
tera	T	10^12
giga	G	10^9
mega	M	10^6
kilo	k	10^3
hekto	h	10^2
deka	da	10'
decy	d	itr^1
centy	c	io-^2
mili	m	lO'^3
mikro	u	1(T^6
nano	n	io-^9
piko	P	lO'^12
femto	f	io-^15
atto	a	io-^18

2

WZORCE JEDNOSTEK MIAR

2.1.WIADOMOŚCI OGÓLNE

2.1.1. Definicje

Wzorce jednostek miar są to narzędzia pomiarowe lub układy pomiarowe przeznaczone do zdefiniowania, zrealizowania, zachowania lub odtworzenia jed­nostki miary lub jej wielokrotności.

Zbiór wzorców miary, które poprzez ich wspólne zastosowanie tworzą wzo­rzec jednostki miary, jest nazywany wzorcem zespołowym jednostki miary.

Zbiór wzorców jednostki miary o wybranych wartościach, które indywidual­nie lub dzięki kombinacji dostarczają szeregu wartości tego samego rodzaju, jest nazywany wzorcem grupowym jednostki miary.

Wzorzec jednostki miary uznany umową międzynarodową za podstawę do przypisywania wartości innym wzorcom jednostki danej wielkości jest nazywany wzorcem międzynarodowym.

Wzorzec jednostki miary uznany urzędowo w danym kraju za podstawę do przypisywania wartości innym wzorcom jednostki miary danej wielkości jest na­zywany wzorcem państwowym.

Wzorzec jednostki miary, który jest ustalony lub powszechnie uznany jako charakteryzujący się najwyższą jakością metrologiczną i którego wartość jest przyjęta bez odniesienia do innych wzorców miary tej samej wielkości jest nazy­wany wzorcem pierwotnym.

Wzorzec jednostki miary, którego wartość jest uzyskana przez porówna­nie z wzorcem pierwotnym jednostki miary tej samej wielkości jest nazywany wzorcem wtórnym.

Wzorzec odniesienia jest to wzorzec jednostki miary o najwyższej jakości metrologicznej w danym miejscu lub danej organizacji, który stanowi odniesienie dla wykonywanych tam pomiarów.

Wzorzec roboczy jest to wzorzec jednostki miary używany do wzorcowania lub sprawdzania przyrządów pomiarowych.

26

2.1.2. Hierarchia wzorców

Odtworzenie wartości jednostki miary danej wielkości odbywa się za pomocą odpowiednich narządzi pomiarowych oraz według ustalonych procedur nazywa­nych systemami sprawdzań narządzi pomiarowych. Systemy te są opisane praw­nie ustalonymi dokumentami.

W zależności od roli jaką pełnią wzorce w procesach pomiarowych tworzą one swoistą piramidę hierarchiczną. Zasady tworzenia tej piramidy wzorców w Polsce pokazano na rysunku 2.1.

Na wierzchołku tej piramidy znajdują się cztery wzorce o najwyższej dokładno­ści: podstawowy, świadek, odniesienia i porównania.

Wzorzec podstawowy jest najczęściej wzorcem zespołowym, składającym się z kilku do kilkunastu wzorców. Jego wartość określa się jako średnią wartość miar wzorców wchodzących w skład zespołu. Wartość wzorca podstawowego ustala się w wyniku porównań z wzorcem międzynarodowym,, np. w Międzyna­rodowym Biurze Wag i Miar (BIPM -Bureau Internationale des Poids et Measu-res) w Sevres.

Wzorzec świadek służy do kontroli stałości wzorca podstawowego lub zastą­pienia go w przypadku uszkodzenia. Jego właściwości metrologiczne nie są gor­sze niż właściwości wzorca podstawowego. Wzorca świadka nie używa się do innych bieżących zadań metrologicznych, nawet do sprawdzania innych wzorców Przez porównanie z wzorcem podstawowym wyznacza się wartości wzorców od­niesienia i porównania..

Wzorzec odniesienia służy do porównywania z wzorcami niższego rzędu pi­ramidy .

Wzorzec porównania służy do komparacji międzynarodowych oraz kompara-cji z innymi wzorcami, które nie mogą być bezpośrednio porównywane. Te cztery wzorce tworzą Państwowy wzorzec jednostki miary danej wielko­ści i jednocześnie pierwszy poziom schematu przekazywania jednostki miary. Wzorce te znajdują się w Głównym Urzędzie Miar (GUM) w Warszawie. Na drugim poziomie są wzorce I-rzędu, które znajdują się w GUM oraz Okręgo­wych Urzędach Miar (OUM).

Trzeci poziom obejmuje wzorce H-rzędu znajdujące się w Okręgowych i Obwo­dowych Urzędach Miar oraz w Laboratoriach Upoważnionych. Z wzorcami tymi porównywane są wzorce i narzędzia pomiarowe znajdujące się u użytkowników. Wzorce użytkowe biorą bezpośredni udział w procesach pomiarowych.

27

BIPM

Wzorzec podstawowy

I GUM

_L

Wzorzec porównania

Wzorzec odniesienia

Wzorzec świadek

Wzorzec I-rzędu

II GUM OUM

Wzorzec Il-rzędu

III GUM OUM Lab.upoważ

Wzorce niższych rzędów oraz narzędzia użytkowe

Rys.2.1. Układ sprawdzeń wzorców jednostki miary

Wymagania

Wymagania stawiane wzorcom jednostek miar:

• niezmienność w czasie,

• duża dokładność,

• łatwa odtwarzalność,

• łatwa porównywalność,

• łatwość stosowania.

Parametry wzorca podawane na tabliczce znamionowej lub jego metryce:

• nominalna miara wzorca,

• niedokładność miary wzorca,

• okres zachowania niedokładności miary wzorca,

• warunki, w których miara i dokładności są zachowane.

W technice pomiarów wielkości elektrycznych, z największą precyzją odtwa­rzane są jednostki miary następujących wielkości:

• siły elektromotorycznej (napięcia),

• rezystancji,

• pojemności,

• indukcyjności własnej i wzajemnej,

• częstotliwości.

28

2.2. WZORCE SIŁY ELEKTROMOTORYCZNEJ I NAPIĘCIA

2.2.1. Ogniwo Westona

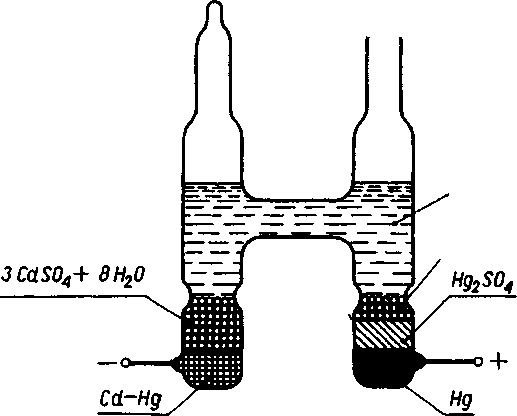
W Polsce wzorcami napięcia stałego (ściślej siły elektromotorycznej) są ogniwa chemiczne Westona. Budowane są dwa typy ogniw: nasycone i nienasy­cone. Budowę ogniwa nasyconego pokazano na rysunku 2.1.

CdSOj 3CdS0₄ + 8H₂0

A

Rys.2. l. Ogniwo Westona

Ogniwo nasycone Westona mieści się w szklanym naczyniu o kształcie zbli­żonym do litery H. Elektrodami ogniwa są druty platynowe wtopione w ramiona naczynia. Biegunem dodatnim ogniwa jest rtęć (Hg), biegunem ujemnym - amal­gamat kadmu (Cd-Hg). Elektrolitem jest nasycony wodny roztwór siarczanu kadmowego (CdSO₄) z nadmiarem kryształów siarczanu kadmu (SCdSCU+SH^O). W całym zakresie użytkowym temperatury elektrolit jest roztworem nasyconym. Biegun dodatni jest pokryty pastą utworzoną z mieszaniny siarczanu kadmu (CdSO4) i siarczanu rtęci (Hg2SO4).Dla ochrony przed wpływem bezpośredniego działania słońca i strumieni ciepła oraz uszkodzeniami mechanicznymi, ogniwa

29

umieszcza się w obudowach wykonanych z masy plastycznej lub metalu. W obu­dowie ogniwa znajduje się gniazdo na termometr umożliwiający pomiar tempe­ratury powietrza wewnątrz obudowy.

Wartość siły elektromotorycznej ogniwa wzorcowego jest zależna, od tempe­ratury.

Dla ogniw nasyconych polska norma PN-80 E-06531 Ogniwa wzorcowe. Wymagania ogólne - podaje wzór pozwalający obliczyć tzw. wartość charaktery­styczną siły elektromotorycznej ogniwa w temperaturze t różnej od temperatury znamionowej t|.

E = E,_i+a(t-ti)+b(t-ti)²+c(t-t_l)³ (2.1)

w którym: E_t - wartość uwierzytelniona, czyli wartość rzeczywista siły

elektromotorycznej, podana w świadectwie sprawdzenia, ti - temperatura znamionowa, t - temperatura ogniwa, a, b, c - stałe, określone oddzielnie dla każdego ogniwa, podane

w świadectwie sprawdzenia.

Np. dla temperatur zawartych w przedziale od 10°C do 30°C, wartości współczynników a, b i c mogą mieć wartości jak we wzorze (2.2)

E, = E₂₀ - 4,06 • 10'⁵ (t - 20)- 0,95 • 10"⁶ (t - 20)² + 0,01 • 10"* (t - 2Qf (2.2)

gdzie: E_t - siła elektromotoryczna ogniwa Westona w temperaturze t °C, E₂o - siła elektromotoryczna ogniwa Westona w temperaturze 20°C.

Wartość uwierzytelniona siły elektromotorycznej w temperaturze równej +20°C wynosi od 1,018540V do 1,018730V, zależnie od jakości użytych mate­riałów.

Temperatura znamionowa ogniwa według normy powinna być wybrana z ciągu wartości: 20°C, 23°C, 25°C lub 28°C.

Wzór (2.1) jest słuszny dla przypadku, gdy „ramiona" ogniwa mają tę samą temperaturę. Ogniwo to ma dużą bezwładność cieplną i stała czasowa ogniwa jest duża, rzędu godzin, zatem wyrównywanie temperatury wszystkich jego elemen­tów może trwać kilkanaście godzin. Z tego powodu z ogniw, które były narażone na zmiany temperatury, można korzystać dopiero po upływie 24 godzin. Okres karencji dotyczy również ogniw narażonych na wstrząsy np. w wyniku transportu.

Z ogniw wzorcowych nie należy pobierać, ani też przepuszczać prądu. Ob­ciążalność ogniw wzorcowych jest bardzo mała. Dopuszczalny krótkotrwały prąd wynosi 1|JA. Dłuższe (już około l minuty) pobieranie prądu o wartości IpA po-

30

woduje odczuwalne zmniejszenie siły elektromotorycznej ogniwa Westona wskutek polaryzacji. Ogniwo odzyskuje właściwą wartość po kilkunastu minu­tach. Przypadkowe zwarcie ogniwa trwające do kilkunastu minut przeważnie nie powoduje trwałego uszkodzenia ogniwa, jednakże przed ponownym użyciem ta­kie ogniwo musi być dokładnie sprawdzone. Pobór prądu o natężeniu większym od lOOfiA trwale uszkadza ogniwo.

Rezystancja wewnętrzna nasyconego ogniwa Westona jest rzędu lk£2. Celem uniknięcia przeciążeń należy dbać o to, by rezystancja obwodu, do którego włą­cza się ogniwo nie była mniejsza niż 9kQ.

Właściwości metrologiczne ogniwa są podstawą do zakwalifikowania go do określonej klasy dokładności. Według normy klasa dokładności to uogólniona charakterystyka ogniw wzorcowych o takiej samej niestabilności czasowej siły elektromotorycznej w czasie, określona po upływie jednego roku od daty pierw­szego sprawdzenia podanej w świadectwie przy spełnieniu warunków przecho­wywania i użytkowania określonych w normie.

Dla ogniw nasyconych norma rozróżnia sześć klas dokładności oznaczonych symbolami:

0,0002; 0,0005; 0,001; 0,002; 0,005; 0,001

lub odpowiednio

2ppm; 5ppm; lOppm; 20ppm; 50ppm; lOOppm.

Liczba będąca wyróżnikiem klasy określa wartość dopuszczalnej rocznej zmiany siły elektromotorycznej ogniwa wyrażonej w procentach wartości nomi­nalnej. Tak określona zmiana nosi nazwę błędu podstawowego ogniwa wzorco­wego.

Definicja błędu podstawowego przybliża ideę oznaczania klasy dokładności za pomocą liter „ppm", które są skrótem od ang. „parts per milion", co w języku polskim oznacza: jedna milionowa (xlO~⁶).

Na obudowie ogniwa wzorcowego umieszcza się następujące dane: znak lub nazwa wytwórcy, typ ogniwa,

numer fabryczny, symbol klasy dokładności, biegunowość zacisków, znamionowa i dopuszczalna pozycja pracy.

Do każdego ogniwa wzorcowego dołącza się świadectwo zawierające nastę­pujące dane:

nazwa lub znak wytwórcy, nazwa i typ ogniwa, numer fabryczny,

31

rodzaj ogniwa (nasycone, nienasycone), symbol klasy dokładności, data sprawdzenia i znak kontroli technicznej,

wartość uwierzytelniona siły elektromotorycznej wraz z niepewnością pomiaru,

temperatura znamionowa,

wartości stałych a, b, c ze wzoru 2. l dla ogniw nasyconych, rezystancja wewnętrzna dla prądu stałego w temperaturze znamionowej. Ogniwa wzorcowe powinny być przechowywane w temperaturze mieszczą­cej się w granicach od 4°C do 40°C.

Źródłem wzorcowego napięcia stałego, niewrażliwym na wstrząsy i wibracje jest ogniwo nienasycone Westona. Elektrolit tego ogniwa jest nienasycony (brak kryształków siarczanu kadmu). Dzięki wkładkom ceramicznym, utrzymującym chemikalia we właściwym miejscu, ogniwo to dobrze spełnia rolę wzorca w urzą­dzeniach przenośnych.

Uwierzytelniona wartość siły elektromotorycznej tego typu ogniw zawiera się w granicach od l,01882 V do 1,01902V w temperaturze 20°C.

Ogniwa nienasycone budowane są w czterech klasach dokładności

0,002; 0,005; 0,01; 0,02 lub

20ppm; 50ppm; lOOppm; 200ppm

Zmiana siły elektromotorycznej ogniwa nienasyconego wraz z temperaturą nie powinna przekraczać 10jiV/⁰C dla temperatur od 4°C do 10°C oraz 5)iV/⁰C dla temperatur powyżej 10°C do 40°C.

Zaletą ogniw nienasyconych jest mała rezystancja wewnętrzna - rzędu 600Q oraz duży dopuszczalny prąd lOOpiA.

Grupowy wzorzec SEM

Jak widać, wymagania stawiane wzorcom jednostek miar lepiej spełniają ogniwa Westona nasycone, dlatego właśnie ogniwa nasycone tworzą Państwowy wzorzec siły elektromotorycznej i napięcia stałego, w skład którego wchodzą: wzorzec podstawowy, wzorzec porównania, wzorzec odniesienia i wzorzec świa­dek (zob. rysunek 2.1).

Wzorzec podstawowy jest wzorcem grupowym (zespołowym) składającym się z grupy 12 ogniw nasyconych, utrzymywanych w stałej temperaturze równej 20°C±0,001°C. Są to ogniwa przechowywane w specjalnych warunkach już od

32

momentu wyprodukowania, tak aby uniknąć wpływu zjawiska histerezy. Zjawi­sko to polega na tym, że wartość SEM ogniwa poddanego zmianom temperatury, wstrząsom nie wraca do uprzedniej wartości.

Jako wartość wzorca jednostki SEM przyjmuje się średnią arytmetyczną wartości sił elektromotorycznych wszystkich ogniw wchodzących w skład grupy. Wartość SEM wzorca ustala się w wyniku porównań w Międzynarodowym Biu­rze Miar i Wag (BIPM) w Sevres, gdzie jej wartość jest odniesiona do wartości ustalonej w oparciu o efekt Josephsona.

Wzorce I-rzędu stanowią pojedyncze ogniwa nasycone Westona.

2.2.2. Źródła wzorcowe wykorzystujące efekt Josephsona

Podstawową wadą ogniw Westona jako wzorców jest to, że są wzorcami sztucznymi, których właściwości zależą od użytych materiałów i technologii wy­konania. Ponadto ich parametry silnie zależą od wpływu warunków otocze­nia, a przede wszystkim zmian temperatury i przyspieszeń. Dlatego dąży się do zdefiniowania jednostki napięcia na podstawie zjawisk molekularnych jako po­wszechnych, praktycznie niezmiennych i prawie nie podlegających wpływom zmian warunków otoczenia. W tym celu prowadzone są intensywne prace nad wykorzystaniem właściwości złącza Josephsona.

Złącze Josephsona składa się z dwóch nadprzewodników rozdzielonych cienką warstwą dielektryka (l-s-2)nm. W temperaturze ciekłego helu 4,2K przez warstwę dielektryczną może przepływać prąd (tzw. prąd tunelowy), będący sumą prądu pojedynczych elektronów i elektronów związanych w pary. Prąd par elek­tronowych i jego oddziaływanie z zewnętrznymi wymuszeniami nadaje złączu wiele interesujących właściwości.

Stałoprądowy efekt Josephsona polega na tym, że przez złącze może prze­pływać prąd stały o wartości mniejszej od pewnej wartości krytycznej Ik nie wy­wołując spadku napięcia na złączu.

Przemiennoprądowy wewnętrzny efekt Josephsona występuje w przypadku umieszczenia złącza spolaryzowanego prądem stałym o wartości większej od wartości krytycznej w słabym (ImT) stałym polu magnetycznym. Wówczas przez złącze, oprócz prądu stałego, płynie również prąd przemienny o częstotliwości zależnej od napięcia U polaryzującego złącze zgodnie z zależnością

(2.3)

w której: e - ładunek elektronu, h - stała Plancka.

33

Szczególnie interesujący z punktu widzenia przydatności złącza do budowy wzorców napięcia jest przemiennoprądowy zewnętrzny efekt Josephsona. Efekt ten występuje po umieszczeniu złącza w polu elektromagnetycznym wielkiej czę­stotliwości f$. W tym przypadku charakterystyka prądowo-napięciowa złącza przybiera kształt schodkowy. Skok prądu występuje przy napięciu U„ spełniają­cym zależność

*tf,=¥-Vn (2-4)

w której: «-kolejny numer schodka.

n=l

U, U₂ U₃ U₄

Rys.2.3. Charakterystyka prądowo-napięciowa złącza Josephsona.

Ostatnia zależność wiąże częstotliwość pola elektromagnetycznego fs z na­pięciem przez stosunek stałych fizycznych e i h. Związek wyrażony równaniem (2.4) jest niezależny od rodzaju nadprzewodnika i dielektryka, od temperatury, od natężenia i intensywności pola magnetycznego. Jest to bardzo istotna cecha tego zjawiska, która predestynuje je do wykorzystania w charakterze wzorca napięcia. Z porównania napięcia U„ z napięciem wzorca (przy znanej częstotliwości) moż­na wyznaczyć stosunek 2e/h i odwrotnie - przy założeniu, że 2e/h ma wartość wyznaczoną z dostateczną dokładnością lub też podaną arbitralnie, złącze można zastosować do odtworzenia i kontroli istniejących wzorców napięcia. Decyzją Międzynarodowego Komitetu Miar i Wag (1.01.1990r.) arbitralnie przyjęto, że:

2e/h=483597,910⁹Hz/V.

Ponieważ częstotliwość fs można zmierzyć stosunkowo łatwo z błędem rzędu 10"⁸%, istnieje więc możliwość bardzo dokładnego porównania „napięcia schód-

34

kowego" U„ z SEM wzorców i wyznaczenia ich zmienności czasowej. Ponadto istnieje możliwość wykorzystania efektu Josephsona do odtwarzania jednostki napięcia. Np. łącząc szeregowo 500 złącz Josephsona można uzyskać napięcie równe 10mV. Zaletą takiego wzorca podstawowego byłaby nie tylko dokładność i stabilność, lecz także to, że byłby on wzorcem absolutnym, tj. wzorcem, którego wartości uzyskane w różnych laboratoriach byłyby jednakowe. Wymagałoby to j ednak zmiany defmicj i j ednostki napięcia.

Stosowanie wzorców ze złączem Josephsona wymaga pokonania trudności technologicznych samego złącza jak również problemów związanych z utrzymy­waniem złącza w temperaturze ok. 4,2K, w której występuje zjawisko nadprze­wodnictwa materiałów złącza, np. stopów niobowo-ołowianych. Także eliminacja sił termoelektrycznych występujących przy tak dużej różnicy temperatur między złączem a otoczeniem , a w szczególności sprawdzanym źródłem, wymaga zasto­sowania odpowiednich środków zaradczych.

Zgodnie z międzynarodowymi zaleceniami wzorce ze złączami Josephsona są coraz szerzej stosowane w laboratoriach Narodowych Biur Miar.

Rys.2.4. Schemat blokowy stanowiska pomiarowego wzorca napięcia ze złączem Josephsona.

Od 1998 roku w Głównym Urzędzie Miar jako wzorzec najwyższego rzędu jednostki miary napięcia elektrycznego wykorzystuje się stanowisko pomiarowe ze złączem Josephsona oraz grupowym wzorcem z diodami Zenera. Uproszczony schemat stanowiska pomiarowego pokazano na rysunku 2.4.

35

Stanowisko pomiarowe wzorca napięcia przedstawione na rysunku 2.4 składa się z następujących podzespołów: naczynia Dewara z ciekłym helem, sondy krio­genicznej ze złączem Josephsona, falowodem i układem mikrofalowym, oscylo­skopu, licznika synchronizującego sterowanego sygnałem zewnętrznej podstawy czasu wzorcowego zegara cezowego, dwóch zestawów wzorców wtórnych oraz komputera z oprogramowaniem NISTYolt.

Znamionowe napięcie wzorca Josephsona jest równe 10V, wzorców wtórnych 10V i 1,018V, a częstotliwość układu mikrofalowego ustalana jest z zakresu (74-77) GHz.

Napięcie we wzorcu Josephsona jest wytwarzane w strukturze około 20 tysię­cy złącz półprzewodnikowych Nb/Al₂O3/Nb z dielektrykiem SiOa. Struktura złącz poddawana jest w temperaturze ciekłego helu (4,2K) działaniu promienio­wania pola elektromagnetycznego o częstotliwości około 75GHz. Promieniowa­nie to jest wytwarzane w generatorze z diodą Gunn'a. Częstotliwość jest mierzo­na licznikiem częstotliwości wysterowanym cezowym wzorcem częstotliwości lOMHz.

W układzie tym uzyskuje się napięcia wzorcowe z zakresu (-10 •*• +10)V. Jed­nostka napięcia przekazywana jest wzorcom wtórnym, którymi są wzorce zbu­dowane na diodach Zenera produkcji firmy Fluke. Jako metodę pomiarową sto­suje się szeregowe przeciwsobne połączenie obu wzorców (Josephsona i Fluke 734A) i pomiar różnicy napięć za pomocą woltomierza cyfrowego.

Stanowisko pomiarowe jest sterowane komputerowo. Program komputerowy NISTYolt umożliwia wykonywanie piętnastu operacji niezbędnych przy stoso­waniu wzorca. Wyniki pomiarów są podawane w postaci tabel i wykresów oraz mogą być drukowane w postaci formalnego raportu.

Według [15] niepewność standardowa względna odtworzenia jednostki napię­cia elektrycznego za pomocą wzorca Josephsona nie przekracza wartości 210"⁹ i wynika z niepewności odtwarzania częstotliwości, natomiast niepewność standardowa względna przekazania jednostki wzorcom wtórnym nie przekracza wartości l O"⁷.

Opisane stanowisko pomiarowe jest produkcji firmy RMC.

2.2.3. Elektroniczne wzorce napięcia stałego

Ogniwo Westona jako źródło napięcia wzorcowego jest mało praktyczne. Mała wartość SEM, niemożność obciążania prądem, delikatna budowa - to wady, które powodują, że coraz częściej jako wzorce użytkowe stosuje się elektroniczne źródła napięcia stałego z diodami Zenera.

36

Dioda krzemowa Zenera jest złączem półprzewodnikowym typu p-n o cha­rakterystyce prądowo-napięciowej jak na rysunku 2.5.

I

AU_Z

U

AI_Z

Rys.2.5. Charakterystyka prądowo-napięciowa diody Zenera.

Dla napięć i prądów dodatnich charakterystyka prądowo-napięciowa jest po­dobna do charakterystyki zwykłej diody krzemowej. Dla napięć i prądów ujem­nych charakterystyka gwałtownie załamuje się przy pewnej wartości napięcia, zwanej napięciem Zenera (Uz). Wartość tego napięcia zależy od typu diody i wy­nosi zwykle od ok. 3V do 27V. W obszarze załamywania się charakterystyki na­stępuje szybki wzrost prądu płynącego przez diodę przy prawie niezmienionym napięciu. Właściwość tę wykorzystuje się do stabilizacji napięcia. Ważnymi parametrami diod Zenera są: współczynnik stabilizacji Sd, rezystancja dynamiczna Rj i współczynnik temperaturowy napięcia stabilizacji (xt.

Współczynnik stabilizacji wyraża stosunek względnych zmian prądu płyną­cego przez diodę do wywołanych przez nie względnych zmian spadku napięcia na diodzie

37

A/,

(2.5)

u,

Dla typowych diod współczynnik ten wynosi ok. 100.

Rezystancja dynamiczna jest to rezystancja dla prądu zmiennego, diody wy-sterowanej prądem stałym o wartości I_z, obliczana według wzoru (2.6)

R -^d ~

(2.6)

Rezystancja ta zależy od wartości napięcia Zenera, zależnej od typu diody i od wartości prądu stabilizacji czyli od punktu pracy. Wartość rezystancji dynamicz­nej wynosi od kilku do kilkudziesięciu omów. Minimalną rezystancję dynamiczną mają diody o napięciu Zenera równym U_z=(6-s-8)V.

Współczynnik temperaturowy napięcia jest zdefiniowany wzorem (2.7).

<x_r =

l At/₂ U₇ AT

•//_z=_c

(2.7)

Współczynnik ten zależy od napięcia Zenera.. Ma on wartość ujemną dla diod o U_Z<5V, a dodatnią dla diod U_Z>7V. Diody o napięciu Zenera U_z=(5-*-7)V mają współczynnik cc_t bliski zeru.

pc']

S-KT¹

10

30

Rys.2.6. Zależność współczynnika temperaturowego od napięcia Zenera

38

Prosty układ wzorcowego źródła napięcia stałego z diodami Zenera przed­stawiono na rysunku (2.7).

-H*

u_we 3

o 1

R₂ R₃

+ -O

D₄

Rys.2.7. Schemat wzorcowego źródła napięcia stałego z diodami Zenera

Napięcie przemienne z transformatora zasilającego jest prostowane przez diody di i Dj, a następnie filtrowane przez filtr składający się z opornika ri i kondensatora d. Oporniki R], R₂ i rs ograniczają prąd płynący przez diody Ze­nera ds i D₄. Przy wzroście napięcia sieci zasilającej wzrasta prąd płynący przez oporniki ri i R₂ oraz diodę ds, zaś napięcie na diodzie da utrzymuje się bez zmian. Dioda D₄ powinna mieć możliwie mały współczynnik temperaturowy oc_t.

Parametrem charakteryzującym jakość elektronicznych źródeł napięcia wzor­cowego jest współczynnik stabilizacji. Określa się go jako stosunek względnej zmiany napięcia wyjściowego do względnej zmiany napięcia wejściowego

A£7

wy

(2.8)

Dla przedstawionego układu przy odpowiednim doborze elementów współczyn­nik ten wynosi od 0,005 do 0,0005.

Na rysunku 2.8 przedstawiono układ wysokostabilnego źródła wzorcowego, wykorzystującego wzmacniacz operacyjny i diodę Zenera. Przy odpowiednim doborze elementów współczynnik stabilizacji tego źródła wynosi ok. l O"⁵. Układ ma zarówno ujemne, jak i dodatnie sprzężenie zwrotne. W chwili włącze­nia wzmacniacz pracuje z silnym sprzężeniem dodatnim, gdyż opornik R\ ma małą rezystancję, a rezystancja początkowa diody D jest duża. W wyniku tego sprzężenia, napięcie na diodzie szybko wzrasta do wartości Uz. Rezystancja dy­namiczna diody jest wtedy mała i wartość sprzężenia dodatniego gwałtownie

39

maleje. W stanie ustalonym wartość napięcia wyjściowego źródła oblicza się z zależności (2.9)

TT _^R2^+R3

(2.9)

Rys.2.8. Schemat wzorcowego źródła napięcia stałego ze wzmacniaczem operacyjnym i diodą Zenera.

Prąd wyjściowy jest ograniczony wartością dopuszczalnego prądu wyjściowego wzmacniacza.

Wzorcowe źródła z diodami Zenera są budowane na różne napięcia znamio­nowe, o wartościach dostosowanych do parametrów układów pomiarowych, z którymi mają współpracować. Prąd wyjściowy (obciążalność prądowa) tych źródeł jest ograniczony tylko parametrami użytych elementów. Zaletą źródeł z diodami Zenera jest niewrażliwość na wstrząsy i wibracje, natomiast wadą tych źródeł-jako wzorców-jest stosunkowo mała stałość w czasie.

Obecnie na świecie wytwarza się półprzewodnikowe źródła napięcia o stabil­ności rocznej dla źródeł o wartości 1,018V około2ppm, a dla źródeł 10V -około l ppm. Źródła te ze względu na łatwość obsługi i przystosowanie do trans­portu są obecnie powszechnie wykorzystywane jako tzw. transfery. Transfery słu­żą do przenoszenia wartości IV lub 10V ze źródeł ze złączami Josephsona na wzorce grupowe zbudowane z ogniw Westona. Również transfery są stosowane

40

w komparacjach międzynarodowych ( porównywanie wartości wzorców pań­stwowych jednostki napięcia różnych krajów), a także przy porównywaniu warto­ści wolta otrzymywanych z różnych stanowisk wykorzystujących złącza Jose-phsona, których bezpośrednie porównanie jest praktycznie niemożliwe.

2.2.4. Kalibratory napięcia

Kalibratory napięcia stałego budowane są jako elektroniczne sterowane źró­dła napięcia stałego, w których wykorzystuje się właściwości wyselekcjonowa­nych diod Zenera. Umożliwiają one otrzymywanie żądanej wartości napięcia z określoną dokładnością bez konieczności mierzenia i ręcznego korygowania nastawień.

Budowane są jako wielozakresowe wzorce użytkowe - np. kalibrator firmy Siemens typu D2300 umożliwia nastawienie napięć w zakresie O-s-lOOOY w czte­rech podzakresach: 0-s-lV, O-IOY, 0-s-100V i (MOOOY, w stopniach co 0,0001 wartości podzakresu. Dopuszczalny pobór prądu dla zakresu pierwszego i drugie­go wynosi lOOmA, dla trzeciego lOmA, dla czwartego zaś ImA. Błąd podstawo­wy kalibratora nie przekracza ±0,008%.

Produkowany w kraju kalibrator typu SQ12 firmy Lumel umożliwia nastawianie napięć w zakresie 0-s-lOY w czterech podzakresach 0-*-10mV, O-s-lOOmY, 0-s-lY i O*l OV, w stopniach co 0,0001 wartości podzakresu. Maksymalne obcią­żenie prądowe dla wszystkich podzakresów wynosi lOOmA.

Schemat strukturalny kalibratora przedstawiono na rysunku 2.9.

Ri U

wy

Rys.2.9. Schemat strukturalny kalibratora napięcia

Żądana wartość napięcia wyjściowego Uwy jest programowana na przełączni­kach bloku nastawy (BN). W zależności od ich położeń wielodekadowy prze­twornik cyfrowo-analogowy (C/A) generuje odpowiednie napięcie wzorcowe,

41

które jest podawane na jedno z wejść komparatora (K). Do drugiego z wejść komparatora jest doprowadzone napięcie sprzężenia zwrotnego. Napięcie sprzę­żenia zwrotnego jest częścią napięcia wyjściowego (dzielnik napięcia ri, R₂). Sy­gnał wyjściowy z komparatora, tzw. sygnał błędu steruje wzmocnieniem wzmac­niacza mocy (W) przez regulator (Reg) i separator transoptorowy (S). Błąd pod­stawowy tego wzorca nie przekracza: ±(0,02% wartości nastawionej +0,005% wartości zakresu +5nV).

Budowane są również precyzyjne kalibratory napięcia przemiennego. Zwykle wykonywane jako uniwersalne, wielofunkcyjne i wielozakresowe wzorce napięć stałych i przemiennych o różnych zakresach częstotliwości. Do czołowych firm produkujących te kalibratory należą J. Fluke, Hewlett-Packard, Siemens, Datron i Lumel.

2.3. WZORCE REZYSTANCJI

Wzorcami rezystancji są bardzo starannie wykonane i dokładnie wywzorco-wane oporniki z drutów i taśm rezystancyjnych. Materiał oporowy z którego wy­konuje się wzorce powinien się charakteryzować poniższymi właściwościami:

duża rezystywność;

mały współczynnik temperaturowy,

mała siła termoelektryczna w styku z miedzią,

stałość oporu w czasie,

duża wytrzymałość mechaniczna i cieplna.

Materiałami spełniającymi te wymagania są stopy miedzi, znane pod nazwami handlowymi manganin i nikrothal. Ich parametry elektryczne są następujące:

manganin nikrothal

współczynnik temperaturowy <2-10"⁵K"' < 1-lO^K"¹

rezystancji

rezystywność ok. 43-10~⁸Qm ok. 133-10'⁸Qm

napięcie termoelektryczne ok. l^Y/K ok. 2jiV/K

w/m miedzi

Dla zapewnienia stałości rezystancji w czasie przeprowadza się sztuczne lub naturalne starzenie materiału oporowego. Starzenie sztuczne polega na wygrze­waniu materiału przez kilkadziesiąt godzin w temperaturze (100-s-150)°C. Starze­nie naturalne polega na wieloletnim przechowywaniu materiału w warunkach znamionowych. Starzenie naturalne jest czasochłonne, a więc kosztowne, jest ono

42

stosowane tylko dla materiałów przeznaczonych do wykonywania wzorców o największej dokładności.

Oporniki wzorcowe powinny mieć następujące właściwości:

dużą dokładność,

stałość rezystancji w czasie,

mała siła elektromotoryczna w styku z miedzią,

mała zależność rezystancji od częstotliwości,

kąt przesunięcia fazowego bliski zeru.

Ostanie dwa wymagania dotyczą wzorców pracujących w układach prądu przemiennego. Spełnienie tych wymagań zależy od konstrukcji opornika ponie­waż przy prądzie przemiennym muszą być brane pod uwagę zjawisko naskórko-wości oraz wpływ resztkowych pojemności i indukcyjności. Naskórkowość zmniejsza czynny przekrój przewodu, a więc zwiększa wartość rezystancji wraz ze wzrostem częstotliwości. Natomiast wpływ resztkowych pojemności i induk­cyjności powoduje, że schemat zastępczy opornika przy prądzie przemiennym ma postać pokazaną na rysunku 2.10.

Rys.2.10. Schemat zastępczy opornika przy prądzie przemiennym Impedancja układu przedstawionego na rysunku 2.10 jest równa

j

(R + j(OL)

₇ jcoC

1

Z = ~ K

JW-L + -

./co -C

gdzie co jest pulsacją prądu przemiennego.

Kąt fazowy między prądem i napięciem oblicza się ze wzoru:

(2.10)

X co(L-/?²c)

= — = — i - i

tf R

(2.11)

43

Przydatność opornika w obwodach prądu przemiennego określa stalą czasowa t.

0)

R

(2.12)

Stała czasowa jest wyrażana w jednostkach czasu. Im mniejsza stała czasowa, tym lepszy jest opornik. Małą wartość stałej czasowej można uzyskać przez od­powiednie ukształtowanie elementu oporowego tak, aby indukcyjność i pojem­ność resztkowa były jak najmniejsze lub przez taki dobór tych wartości, aby speł­niona była zależność (2.13).

L_ ~R

(2.13)

Zmniejszenie indukcyjności resztkowej można uzyskać stosując uzwojenie bifilarne. Przewód oporowy tworzy długą pętlę o małej powierzchni. Kierunki prądu w przewodach leżących obok siebie są przeciwne, tak jak pokazano na ry­sunku 2.11 a.

Rys.2.11. Sposoby nawijania oporników; a) nawinięcie bifilarne, b) nawinięcie Chaperona.

Przy nawinięciu bifilarnym opornik charakteryzuje się dużą pojemnością, dlatego ten sposób nawinięcia można stosować w opornikach o rezystancji mniej­szej lub równej 100Q. W opornikach o większej rezystancji stosuje się uzwojenie Chaperona. Uzwojenie to jest nawinięte w kilku sekcjach na korpusie w kształcie walca, (rysunek 2.11.b). Każda sekcja ma dwie warstwy zwojów, przy czym gór­na warstwa jest nawinięta w kierunku przeciwnym niż dolna, tak że strumienie magnetyczne prądów płynących przez opornik znoszą się. W praktyce stosuje się jeszcze inne rodzaje uzwojeń jak np. uzwojenie Ayrtona czy plecione.

Stała czasowa oporników wzorcowych, w zależności od klasy dokładności, zawarta jest w przedziale 10~⁶s + 10~⁸s.

44

W obwodach prądu przemiennego opornik jest reprezentowany przez impe-dancję Z, tymczasem przyjmuje się ,że ma on tylko rezystancję -/?„. Błąd spowo­dowany zaniedbaniem reaktancji opornika przy prądzie przemiennym, można wyznaczyć za pomocą wzoru

8_T = ^Z~^R" = r-y/l + (w-T)² -1]. 100% (2.14)

R„ L J

Przy częstotliwościach technicznych ( ok. 50Hz) wpływ stałej czasowej jest pomijamy, jednak przy dokładnych pomiarach uwzględnia się go już przy często­tliwościach powyżej lOOHz.

Najczęściej spotykany podział wzorców to: wzorce nienastawne odtwarzają­ce jedną wartość rezystancji - zwane opornikami wzorcowymi, i wzorce nastawne, odtwarzające wiele wartości rezystancji - zwane opornikami dekadowymi.

2.3.1. Oporniki wzorcowe jednostopniowe.

Oporniki wzorcowe powinny spełniać wymagania normy PN-90 E-06509 Oporniki wzorcowe. Ogólne wymagania i badania. Norma ta podaje poniższe określenia.

Opornik wzorcowy jest to rezystor lub zespół rezystorów odwzorowujący określoną wartość rezystancji między zaciskami napięciowymi opornika.

Wartość znamionowa rezystancji R„ - wartość rezystancji podana na oporni­ku.

Wartość umowna rezystancji R_um- wartość rezystancji, w stosunku do której wyznacza się błąd opornika. Za wartość umowną przyjmuje się:

wartość uwierzytelnioną dla oporników o wskaźnikach klas dokład­ności 0,0005-5-0,01, (Sppm-s-lOOppm),

wartość znamionową dla oporników pozostałych o wskaźnikach 0,02-5-0,2 (200ppm-5-2000ppm).

Wartości znamionowe rezystancji R„ oporników wzorcowych są podwielo-krotnością lub wielokrotnością l Q zgodnie ze wzorem

R_n=lO"-lQ, (2.15)

w którym p jest liczbą całkowitą z przedziału (-4-H-7).

45

Jednym z podstawowych parametrów metrologicznych oporników, decydu­jących o ich przydatności w układach pomiarowych prądu stałego, jest bląd pod­stawowy zdefiniowany następująco

§=^R~^R<"» 100% (2.16)

^Rum

gdzie: R - wartość rzeczywista (poprawna) rezystancji opornika, wyznaczona w warunkach znamionowych (odniesienia); Rum - wartość umowna rezystancji opornika.

Warunki odniesienia podaje norma , a dotyczą one wartości takich parame­trów jak:

temperatura otoczenia 23°C, wilgotność względna powietrza 50%, moc obciążenia - wartość dowolna w zakresie znamionowym; rodzaj prądu, pozycja pracy,

natężenie zewnętrznego pola magnetycznego 40A/m, chłodzenie - naturalne.

W zależności od wartości błędów podstawowych norma PN-90/06509 roz­różnia 9 klas dokładności oporników wzorcowych, o wskaźnikach:

0,0005; 0,007; 0,002; 0,005; 0,07; 0,02; 0,05; 0,7 i 0.2. Przy tym, wskaźnik klasy jest równy liczbowo wartości granicznej błędu podstawowego wyrażonego w procentach lub ppm. Np. dla opornika klasy 0,0005 błąd podstawowy wyznaczony w warunkach odniesienia nie powinien przekra­czać ±0,0005%, (lub ±5 ppm), dla opornika klasy 0,001 nie powinien przekraczać ±10 ppm itd.

Elementy te umieszcza się w obudowach wykonanych z metalu lub masy pla­stycznej, mających kształt kubka z pokrywą izolacyjną i zaciskami. Często w pokrywie znajduje się gniazdo umożliwiające umieszczenie termometru. Otwory w obudowie ułatwiają chłodzenie elementu rezystancyjnego po zanurzeniu opor­nika w cieczy chłodzącej (olej, nafta).

Ważnym parametrem oporników wzorcowych jest ich obciążalność, wyraża­na za pomocą dopuszczalnej mocy wydzielanej na oporniku wzorcowym. War­tość mocy dopuszczalnej zależy od warunków chłodzenia. W powietrzu wynosi najczęściej Pd_0p=lW, zaś w kąpieli cieczowej P_dop=3W. Moc ta określa dopusz­czalne wartości prądu jaki może płynąć przez opornik, zgodnie z zależnością

46

(2.17)

Przekroczenie wartości dopuszczalnej prądu może spowodować trwałą zmia­nę rezystancji opornika lub jego zniszczenie. Utrzymanie mocy obciążenia i tem­peratury otoczenia we właściwych granicach jest niezbędnym warunkiem prawi­dłowego użytkowania oporników wzorcowych.

Oporniki wzorcowe mają dwie pary zacisków: dwa zaciski prądowe i dwa zaciski napięciowe. Zaciski prądowe służą do doprowadzenia prądu do opornika, zaś zaciski napięciowe - do pomiaru napięcia na oporniku. Rezystancja opornika jest zawarta między zaciskami napięciowymi.

/ l > o—

Rys.2.12. Schemat elektryczny opornika wzorcowego; 1,2 -zaciski prądowe, 3,4 - zaciski napięciowe.

Stosowanie zacisków prądowych i napięciowych zmniejsza błędy spowodo­wane wpływem rezystancji przejściowych na stykach przewodów łączących i za­ciskach, zwłaszcza tam, gdzie są one porównywalne z wartością rezystancji opor­nika wzorcowego. Oporniki wzorcowe o rezystancji powyżej Ikfi! mogą mieć tylko dwa zaciski.

Zaciski oporników prądu przemiennego powinny być oznaczone literami L i H. Literą L oznacza się zacisk, który w układzie pomiarowym powinien mieć niższy potencjał.

Oporniki wzorcowe są budowane na określoną częstotliwość znamionową prądu. Częstotliwość ta jest wybrana z następującego szeregu:

50, 100, 200, 500 Hz 1,2,5,10,20,50,100 kHz.

Stałe czasowe oporników wzorcowych powinny być mniejsze od wartości podanej przez wytwórcę, wybranej z szeregu:

1,2,5,10 100 ns.

47

2.3.2. Oporniki wzorcowe regulowane

Opornikiem dekadowym nazywa się zespół dekad umieszczonych we wspól­nej obudowie.

Dekada jest to grupa oporników z przełącznikiem (najczęściej pokrętnym lub kołkowym) umożliwiającym nastawianie rezystancji o wartości równej zero oraz z mnożnikiem równym kolejnym liczbom naturalnym od l do 9, 10 lub 11.

Oporniki dekadowe z przełącznikiem pokrętnym mają 10 lub 9 jednakowych elementów oporowych połączonych ze sobą szeregowo. Poniżej przedstawiono układ połączeń opornika czterodekadowego.

Rys.2.13. Układ połączeń opornika dekadowego z przełącznikiem pokrętnym

Oporniki z przełącznikiem kołkowym, mają układ wagowy oporników. W obrębie dekady są cztery oporniki o różnych wartościach, np. (l+2+3+4)xlO^pQ, lub (l+2+2+5)xlO^pQ, gdzie p=±l,+2,+3..., połączone ze sobą szeregowo oraz każdy z nich odpowiednio do gniazda przewodzącego, umożli­wiającego jego zwarcie za pomocą stożkowego kołka wykonanego z mosiądzu (zobacz rysunek 2.14). Regulacja wartości nastawionej polega na zwieraniu koł­kami lub rozwieraniu elementów oporowych o odpowiednich wartościach, tak aby suma rezystancji niezwartych elementów była równa żądanej.

Na stykach między kołkiem a gniazdem występuje zawsze pewien opór (rzę­du lmQ). Jego wartość zależy od siły z jaką kołek został wciśnięty oraz od jako­ści wykonania i stanu stykających się powierzchni. Z tego względu należy bardzo starannie konserwować stykające się powierzchnie.

48

Rys.2.14. Budowa dekady w oporniku kołkowym

Oporniki dekadowe buduje się najczęściej jako zestawy cztero- lub sześcio-dekadowe. Ze względów technologicznych najmniejszy stopień dekady jest rów­ny O, l Q, a największy 1MQ.

Błędy oporników dekadowych, zarówno przy prądzie stałym, jak i przemien­nym, określa się w taki sam sposób jak błędy oporników wzorcowych. W zależ­ności od wartości tych błędów norma PN-90/E-06508 Oporniki dekadowe. Ogól­ne wymagania i badania, rozróżnia dziewięć klas dokładności oporników deka­dowych:

0,01; 0,02; 0,05; 0,1; 0,2; 0,5; 1; 2 i 5.

Klasę opornika dekadowego należy rozumieć w ten sposób, że dekada o najwięk­szej wartości jest wyrażona z błędem (wyrażonym w procentach ) liczbowo rów­nym symbolowi klasy. Dekady o opornikach mniejszych są wykonywane mniej dokładnie.

Ze względu na nienajlepsze warunki chłodzenia elementów oporowych w opornikach dekadowych dopuszczalne obciążenie poszczególnych cewek (ele­mentów oporowych) jest zawarte w przedziale (0,5*l)W/cewkę oporową. Stąd największe ograniczenie prądu mają oporniki (cewki) o największej rezystancji.

2.3.3. Państwowy wzorzec oporu elektrycznego

Państwowy wzorzec oporu elektrycznego składa się z czterech wzorców o najwyższej dokładności: podstawowego, świadka, porównania i odniesienia (zob. rys.2.1). W Polsce w skład wzorca podstawowego wchodzi sześć oporników wzorcowych o wartości nominalnej l Q. Jako wartość oporu wzorcowego przyj­muje się średnią arytmetyczną ze wszystkich wartości oporu oporników wcho­dzących w skład grupy. Wartość tę uznaje się za niezmienną w okresie między dwoma jej wyznaczeniami na drodze porównań z wzorcem międzynarodowym. Wzorzec podstawowy zapewnia odtwarzanie jednostki oporu elektrycznego

49

z odchyleniem średnim kwadratowym wyniku pomiaru nie gorszym niż 1-10"⁷ (przy liczbie pomiarów nie mniejszej niż 10).

Wzorce świadek i porównania są również wzorcami grupowymi, utworzo­nymi z oporników o wartości nominalnej równej l Q.

Wzorzec odniesienia tworzy grupa oporników wzorcowych o wartościach nominalnych od 10"³Ś2 do!0⁷Q.

Wartość jednostki oporu za pomocą precyzyjnych komparatorów, mostków, kalibratorów i multimetrów jest przekazywana wzorcom niższych rzędów ( także wzorcom pracującym w układach prądu przemiennego.

Zgodnie z zasadą aby wzorce miary były określone ze zjawisk molekular­nych jako niezmiennych w czasie, są prowadzone nad budową wzorca rezystancji opartego na kwantowym efekcie Halla (QHR) odkrytym przez Klausa von Klit-zingaw!980r.

Kwantowy efekt Halla występuje w półprzewodnikowych płytkach o struktu­rach np.AlGaAs-GaAs lub InGaAs-InP ochłodzonych do temperatury 0,36K. Je­żeli płytkę taką, zasilaną w kierunku osi x prądem stałym o wartości I=10nA umieści się w silnym polu magnetycznym, którego wektor indukcji (B=12,6T) jest skierowany w kierunku osi z, to rezystancja w kierunku osi y jest równa

_fl

^y 2e²n n gdzie: A-stała Plancka; e-ładunek elektronu; n-2 lub 4.

Ponieważ wartości h i e zostały przyjęte arbitralnie (decyzja Międzynarodo­wego Biura Miar i Wag z 1972r), więc rezystancja płytki jest stała i niezależna od czasu. Wzorce tego typu umożliwiają odtworzenie jednostki rezystancji z błędem od l do 3- 1 0"⁸ (l ppm do 3- 1 0"² ppm ) i służą do kontroli stałości w czasie wzor­ców użytkowych.

2.4. WZORCE POJEMNOŚCI

Wzorcami pojemności są kondensatory wzorcowe. Kondensatorom tym sta­wia się następujące wymagania:

dokładna wartość pojemności, stałość pojemności w czasie, niezależność pojemności od temperatury, niezależność pojemności od częstotliwości, mały współczynnik stratności.

50

Wymagania te najlepiej spełniają kondensatory powietrzne i próżniowe o prostych geometrycznie kształtach. Są to wzorce liczalne, tj. kondensatory wzorcowe, których pojemność jest obliczana na podstawie wymiarów geome­trycznych, wyznaczonych z dużą dokładnością oraz znajomości stałej dielek­trycznej próżni. Najczęściej są to kondensatory płaskie o kolistym kształcie elek­trod lub kondensatory cylindryczne. Elementy konstrukcyjne utrzymujące elek­trody we właściwym położeniu są wykonywane z materiałów o dużej rezystyw-ności (p=10¹⁶Qm) takich jak kwarc lub bursztyn. Elektrody kondensatorów są umieszczane w metalowym ekranie, by ustalić pojemności względem otoczenia, tak jak pokazano na rysunku 2.15.

Rys.2.15. Schemat zastępczy ekranowanego wzorca pojemności

Wzorzec ma trzy zaciski: dwa z nich (l oraz 2) są przyłączone do elektrod, a trzeci (0) do ekranu. Jeśli zacisk O jest połączony z zaciskiem l, to pojemność kondensatora wzorcowego między zaciskami l i 2 jest równa

C — C

*- ~*-

(2.19)

gdzie: C\i - pojemność między elektrodami kondensatora, C₂o - pojemność między elektrodą 2 a ekranem.

Jeżeli połączy się ze sobą zaciski O i 2, to pojemność kondensatora wzorcowego między zaciskami l i 2 jest równa

'10

12

C = C,, + C

(2.20)

51

gdzie: Cio - pojemność między elektrodą l a ekranem.

Wartości pojemności C\2, C\$ oraz €20 są podawane na tabliczce znamionowej wzorca.

W idealnym kondensatorze (bezstratnym) kąt przesunięcia fazowego (p mię­dzy prądem a napięciem wynosi n/2. W kondensatorach rzeczywistych występują straty na histerezę dielektryczną i straty cieplne. Straty te wynikają przede wszystkim z właściwości dielektryka i elementów konstrukcyjnych: izolatorów i doprowadzeń. Jakość rzeczywistego kondensatora określa kąt strat dielektrycz­nych S lub współczynnik strat dielektrycznych tg8.

= TC/2-<p

(2.21)

Kondensator rzeczywisty można przedstawić za pomocą układu zastępczego szeregowego lub równoległego zawierającego pojemność i rezystancję.

a)

b)

u

tg8 =

u>C_pU ti>R_pC„

ooC,

Rys.2.16. Układy zastępcze kondensatora ze stratami; a) równoległy, b) szeregowy

52

Kąt strat dielektrycznych 8, charakteryzujący jakość kondensatora zależy od częstotliwości i od napięcia przyłożonego do kondensatora. Dlatego też tg8 wzor­ców pojemności jest podawany dla znamionowej częstotliwości i znamionowego napięcia.

Właściwości dielektryczne powietrza są zbliżone do właściwości dielektryka doskonałego (bezstratnego), stąd też kondensatory powietrzne charakteryzują się bardzo małym tgd (tgó * 1-lff⁵ przy częstotliwości/ = IkHź).

Budowane są powietrzne kondensatory wzorcowe o wartościach pojemności od kilku pF do lOOOOpF.

Wzorce odniesienia odtwarzają jednostkę pojemności z błędem względnym <H(T⁵%(0,lppm).

Roczne względne zmiany pojemności kondensatorów wzorcowych wynoszą < 0,2ppm.

Zmianę pojemności pod wpływem temperatury określa współczynnik tempe­raturowy pojemności, który dla kondensatorów wzorcowych jest rzędu ok. 2-l(T⁶/K.

Kondensatory powietrzne są budowane na napięcia znamionowe: 250V-500kV.

Wadą kondensatorów powietrznych jest mała wartość pojemności przy jed­nocześnie dużych wymiarach. Dlatego kondensatory wzorcowe o pojemnościach większych od lOOOOpF są budowane z dielektrykiem mikowym. Dzięki dużej przenikalności dielektrycznej oraz dużej wytrzymałości na przebicie, wymiary i masa wzorców mikowych są znacznie mniejsze niż wzorców powietrznych. Wy­konuje się wzorce mikowe o pojemności do 10 pF. Ich tg 6 < 5-1 ff⁴ przy często­tliwości/= 7 kHz.

Obecnie buduje się wzorce polistyrenowe ( styrofleksowe ), których właściwości są zbliżone do właściwości kondensatorów mikowych.

Wzorce mikowe i styrofleksowe są wykonywane jako dekadowe wzorce nastaw­ne. Schemat połączeń dekady wzorca o regulowanej pojemności pokazano na ry­sunku 2.17.

Zwykle największy stopień dekady wzorca pojemności wynosi l [iF, naj­mniejszą dekadą zaś jest obrotowy kondensator powietrzny umożliwiający płynne nastawianie pojemności w zakresie 0+ WOpF. Wzorce nastawne budowane są jako zestawy cztero-, pięcio- lub sześciodekadowe, najczęściej w klasie 0,1 lub 0,5.

HH*

53

Rys.2.17. Schemat połączeń dekady pojemności.

2.5.WZORCE INDUKCYJNOŚCI

2.5.1.Wzorce indukcyjności własnej

Wzorcami indukcyjności własnej są cewki nawinięte jedno- lub wielowar­stwowo na korpusach z materiałów o minimalnym współczynniku rozszerzalności temperaturowej, np. z marmuru, porcelany lub szkła. Ze względu na zjawisko na-skórkowości cewki nawijane są przewodem skręconym z wielu cienkich przewo­dów miedzianych (tzw. lica), izolowanych emalią lub jedwabiem. Wzorce te na­leżą do wzorców liczalnych tzn. takich, których wartość można obliczyć na pod­stawie liczby zwojów i wymiarów geometrycznych uzwojenia.

Budowane są wzorce indukcyjności o wartościach od lOjiH do 10H. Błąd względny odtworzenia jednostki przez wzorzec odniesienia wynosi 5-10"⁴%, (5 ppm). Błędy wzorców użytkowych nie przekraczają zwykle 0,02%. Względne zmiany indukcyjności na skutek zmian temperatury (zmiana wymiarów geome­trycznych ) są mniejsze niż 4 ppm/K.

Indukcyjność wzorca zależy od częstotliwości. Jest to wywołane przede wszystkim przez pojemności międzyzwojowe oraz - w mniejszym stopniu - przez prądy wirowe i straty dielektryczne w izolacji. Pojemności między zwojami moż­na przedstawić w uproszczeniu jako pojemność skupioną włączoną między zaci­ski wzorca. Schemat zastępczy wzorca indukcyjności jest więc taki sam jak schemat zastępczy opornika wzorcowego.

54

Rys.2.18. Schemat zastępczy wzorca indukcyjności własnej

Przy częstotliwościach bliskich częstotliwości rezonansowej reaktancja in­dukcyjna układu wzrasta szybciej niż częstotliwość. Jest to równoznaczne ze zwiększaniem się indukcyjności wypadkowej ze wzrostem częstotliwości. Wzor­ce indukcyjności powinny być używane przy częstotliwościach znacznie mniej­szych niż częstotliwość rezonansowa. Zwykle wartość indukcyjności wzorca jest podawana dla konkretnej częstotliwości, najczęściej dla l kHz.

Jednym z parametrów charakteryzujących jakość wzorców indukcyjności jest dobroć Q, obliczana według wzoru

i= ®L R

(2.22)

Budowane obecnie wzorce mają dobroć od 50 do 200, przy f=lkHz.

Oprócz wzorców jednomiarowych budowane są wzorce indukcyjności na­stawne w postaci zestawów dekadowych. Układ połączeń dekady indukcyjności pokazano na rysunku 2.19.

Rys.2.19. Układ połączeń dekady indukcyjności

55

Szeregowo z cewkami są włączone oporniki, dzięki czemu rezystancja deka­dy ma wartość stałą, prawie niezależną od wartości nastawionej indukcyjności. Wzorce te są nawijane na toroidalnych rdzeniach ferromagnetycznych o stosun­kowo niewielkiej względnej przenikliwości magnetycznej (rzędu 20-5-50). Wartość indukcyjności tych cewek zależy w pewnym stopniu od wartości przepływającego prądu. Dlatego też błędy wzorców nastawnych są większe od błędów wzorców nienastawnych. Wynoszą one od 0,1% do 2%.

2.5.2. Wzorce indukcyjności wzajemnej

Wzorce indukcyjności wzajemnej uzwaja się podobnie jak wzorce indukcyj­ności własnej, ale dwoma przewodami jednocześnie. Istnieją również wzorce, których uzwojenia są umieszczone w oddzielnych przegrodach korpusu. Budo­wane są na wartości od Imffdo l H.

Buduje się również regulowane wzorce indukcyjności wzajemnej. Do takich wzorców należy wariometr. Składa się on z dwu okrągłych cewek: ruchomej i nieruchomej. Cewka ruchoma, którą można obracać dookoła osi, jest umiesz­czona wewnątrz cewki nieruchomej. Indukcyjność wzajemna obu cewek zmienia się w zależności od kąta, pod jakim przecinają się płaszczyzny cewek i równa się zeru, gdy płaszczyzny cewek są prostopadłe względem siebie. Jeśli kąt między płaszczyznami jest większy niż 90°, to indukcyjność wzajemna zmienia znak. Niektóre wariometry umożliwiają zmianę indukcyjności wzajemnej w granicach odO,0004HdoO,2H.

W układach pomiarowych, w które są włączone cewki wzorcowe należy zwrócić uwagę na to, by wartość prądu płynącego przez cewkę nie przekroczyła wartości dopuszczalnej dla cewki, którą podaje producent. Np. cewka wzorcowa indukcyjności własnej produkcji firmy Norma-Wien o L„=1H ma dopuszczalny prąd 0,25A, a cewka indukcyjności wzajemnej tej samej firmy dla L„=10mH ma prąd dopuszczalny l A.

2.6. ŹRÓDŁA CZĘSTOTLIWOŚCI WZORCOWYCH

W zależności od przeznaczenia, źródła częstotliwości wzorcowych dzielą się na wzorce odniesienia, kontrolne i użytkowe.

Wzorcami odniesienia są atomowe wzorce cezowe, rubidowe oraz masery wodorowe.

56

Wzorcami kontrolnymi są generatory kwarcowe oraz zespoły aparatury do nadawania sygnałów wzorcowej częstotliwości drogą radiową i przewodową. Wzorcami użytkowymi są generatory pomiarowe, zegary, stopery itp.

Cezowy wzorzec częstotliwości

Cezowy wzorzec częstotliwości realizuje fizyczną definicję sekundy, czyli jednostki czasu, a zarazem jest wzorcem częstotliwości ponieważ częstotliwość jest powiązana prostą zależnością z czasem.

Sekunda jest to czas równy 9192631770 okresów drgań pola elektromagne­tycznego jednoznacznie odwzorowującego przejście między stanami energetycz­nymi F=4 i F=3 swobodnych atomów cezu 133.

Zgodnie z powyższą definicją, wzorzec ten pracuje na zasadzie porównania częstotliwości drgań bardzo stabilnego generatora kwarcowego z częstotliwością rezonansową linii absorbcyjnej atomów cezu. Linia ta jest uzyskiwana w spek­trometrze masowym, przez który przebiega wiązka atomów tego pierwiastka.

Zasadę działania wzorca odniesienia ilustruje schemat funkcjonalny cezowej lampy promieniowej przedstawiony na poniższym rysunku.

Ekrany magnetyczne

-

":::z:/:::::..

Ki

mim x>&!

ra

Piec cezowy

Selektor magnetyczny I

Selektor magnetyczny II

Detektor promenio-wania

miki

owa

-

,

Powielacz jonów

Spektrometr masowy

1

Wyjście

Wejście mikrofalowe f=9192631770Hz

Rys.2.20. Schemat funkcjonalny cezowej lampy promieniowej

Piec cezowy jest źródłem odpowiednio uformowanej wiązki atomów cezu o wymaganej temperaturze. Wiązka ta, za pomocą kolimatora umieszczone­go tuż za piecem, jest kierowana w obszar oddziaływania selektora magnetyczne­go I. Magnesy tego selektora powodują zmiany poziomów energetycznych ato-

57

mów cezu. Przy braku zewnętrznego pola magnetycznego w wiązce występują atomy tylko o dwóch poziomach energetycznych F=4 i F=3. Jednakże już w polu o indukcji B=6-10~⁶T (wytworzonym przez magnesy selektora I) atomy grupy o większej energii (F=4) mogą przyjąć jeden z 9 nadsubtelnych poziomów, atomy zaś o mniejszej energii (F=3) mogą przyjąć jeden z 7 poziomów. Przy dużej in­dukcji pola magnetycznego atomy o podpoziomie energetycznym F=4, niF=-4 (F i mp - liczby kwantowe) przechodzą do grupy F=4. Różnica energii między pozio­mami F=4 i F=3 jest opisana wzorem Einsteina

&W=hf (2.23)

gdzie: h - stała Plancka,

/- częstotliwość przejścia.

Przejście atomów cezu z jednego stanu energetycznego do drugiego jest związane z rezonansowym pochłanianiem energii w komorze mikrofalowej, po­budzonej do drgań o częstotliwości/=9192631770 Hz,

Selektor magnetyczny II wytwarza silne, niejednorodne pole magnetycz­ne o indukcji B=1T. W polu tym atomy cezu ulegają odchyleniu w zależności od ich energii. Atomy o podpoziomach energetycznych F=3 i atomy o podpozio-mach F=4, mp=-4 są odchylane w obszar pola o większej indukcji, pozostałe zaś w obszar pola o mniejszej indukcji. Selektor magnetyczny II separuje więc prze­strzennie te dwie grupy atomów. Po wyjściu z komory mikrofalowej i przejściu przez pole wytwarzane przez magnesy selektora II, wiązka atomów o podpozio­mie energetycznym F=4, m_F=4 trafia przez detektor promieniowania do spektro­metru masowego, który przestrzennie separuje jony cezu od jonów innych pier­wiastków stanowiących szumy. Stąd wiązka jest przesyłana na powielacz, który wzmacnia sygnał prądowy (rzędu l O"¹² A) do poziomu wyższego od poziomu szumów. Prąd wyjściowy ma składową stałą i składową przemienną o częstotli­wości 137 Hz.

Sygnał wyjściowy cezowej lampy promieniowej ma małą moc. Dlatego wzo­rzec cezowy nie jest stosowany bezpośrednio, lecz pośrednio - najczęściej do sta­bilizacji częstotliwości stabilnego wzorca kwarcowego. Schemat struktury takiego wzorca przedstawiono na rysunku 2.21.

Podstawowym podzespołem tego wzorca jest stabilny generator kwarcowy generujący napięcie o częstotliwości f_w= 5MHz. Sygnał wyjściowy z generatora jest podawany do układu dwoma torami. W jednym torze sygnał o częstotliwości f„ przez wzmacniacz dochodzi do syntetyzera. Z syntetyzera sygnał o częstotli­wości//= 12,631770MHz jest podawany do generatora harmonicznych.

58

Rys.2.21.Schemat struktury cezowego wzorca częstotliwości

W drugim torze sygnał/,, jest modulowany częstotliwościami/ = 90MHz oraz/= 137Hz i również podawany do generatora harmonicznych. W generab-rze następuje mieszanie sygnałów o częstotliwościach/ i/, w wyniku czego na jego wyjściu pojawia się sygnał o częstotliwości/ = 9,192631770 GHz, a więc sygnał o częstotliwości rezonansowej atomów cezu. Sygnał o częstotliwości/ jest następnie podawany do cezowej lampy promieniowej (ściślej do jej komory mikrofalowej).

Jeżeli częstotliwość /, jest równa 5MHz, to częstotliwość / jest równa czę­stotliwości rezonansowej cezowej lampy promieniowej, a pad wyjściowy lampy zawiera składową stałą i składową zmienną o częstotliwości/ = 137Hz. Jeżeli częstotliwość/, różni się od 5MHz, to prąd wyjściowy zawiera składowe harmo­niczne, których amplituda dostarcza informacji o różnicy między częstotliwością /, a 5MHz, faza zaś informuje o znaku tej różnicy.

Prąd wyjściowy z cezowej lampy promieniowej po wzmocnieniu jest dopo-wadzany do detektora, gdzie jest porównywany z sygnałem o częstotliwości /= 137Hz. Otrzymany z detektora sygnał b^du koryguje częstotliwość /,= 5 MHz generatora kwarcowego.

Tak skonstruowany wzorzec wytwarza sygnał wzorcowy o csęstotliwości 5MHz z błędem względnym niniejszym niż ±MO"¹³.

3

METODY POMIAROWE

3.1. OGÓLNA CHARAKTERYSTYKA METOD

Terminem metoda pomiarowa określa się sposób porównywania wielkości stosowany przy wykonywaniu pomiaru.

Każdą wielkość fizyczną można mierzyć różnymi sposobami korzystając z różnych metod. Wybór metody jest uzależniony od wartości wielkości mierzo­nej, jej rodzaju, wymaganej dokładności, wykorzystania wyniku pomiaru, itp.

Klasyfikacja metod pomiarowych może być dokonywana w bardzo różno­rodny sposób. Wydaje się, że najbardziej celowe będzie dokonanie klasyfikacji, mając na uwadze charakterystyczne cechy metrologiczne i użytkowe. Z tego punktu widzenia metody pomiarowe można podzielić:

1. według przetwarzania sygnału pomiarowego w procesie pomiarowym,

2. według uzyskiwania wyniku pomiaru,

3. według porównania realizowanego w trakcie procesu pomiarowego.

3.2. METODY ANALOGOWE I CYFROWE

Ze względu na sposób przetwarzania sygnału pomiarowego w procesie po­miarowym, metody pomiarowe można podzielić na metody analogowe i cyfrowe.

Metoda analogowa polega na tym, że wartości wielkości mierzonej, zmie­niającej się w sposób ciągły, jest przyporządkowana wartość zmieniająca się też w sposób ciągły jak np. odchylenie organu ruchomego miernika. W metodzie cy­frowej - ciągłym podziałom wartości wielkości mierzonej są podporządkowane dyskretne (nieciągłe) przedziały wartości wielkości wyjściowej. Wielkość wyj­ściowa ma formę kwantów. Metoda cyfrowa charakteryzuje się zamianą wielko­ści wejściowej na dyskretną, nieciągłą wartość wyjściową podawaną w formie cyfrowej.

Jeżeli odbiorcą wyniku pomiaru w metodzie cyfrowej jest człowiek, to sto­suje się zapis dziesiętny. Jeżeli odbiorcą jest komputer wynik pomiaru podany jest w kodzie dwójkowym.

60

3.3. METODY BEZPOŚREDNIE I POŚREDNIE

Ze względu na sposób uzyskiwania wyniku pomiaru metody pomiarowe można podzielić na bezpośrednie i pośrednie.

Metoda jest bezpośrednia, jeżeli wartość wielkości mierzonej otrzymuje się bezpośrednio bez wykonywania dodatkowych obliczeń. Przykładem może być pomiar napięcia woltomierzem, lub pomiar oporu elektrycznego omomierzem, pomiar czasu sekundomierzem, itp. Przyjmuje się, że metoda pomiarowa jest bezpośrednia w przypadku, gdy podziałka przyrządu podaje wartości umowne związane, w postaci wykresu czy tablic, z wartościami wielkości mierzonej bądź, gdy zachodzi potrzeba wykonywania dodatkowych pomiarów w celu np. wyzna­czenia wpływu czynników zewnętrznych tak, aby można było wprowadzić po­prawki. Trzeba jednak mieć na uwadze fakt, że poprawkę oblicza się zaw­sze z pewnym błędem, ponieważ parametry przyrządów, na podstawie wskazań których oblicza się poprawkę, są znane z pewnym przybliżeniem.

W metodzie pośredniej wartość wielkości mierzonej otrzymuje się pośrednio z pomiarów bezpośrednich innych wielkości związanych znaną zależnością funk­cyjną z wielkością mierzoną

Y = f(X_l,X₂,X„...X_N) (3.1)

Wielkości X_l,X₂,X₃,...X_N są mierzone bezpośrednio. Przykładem może być pomiar rezystancji metodą techniczną w układzie z woltomierzem i amperomierzem

* = y (3-2)

Zależność funkcyjna, jej postać, ma bezpośredni wpływ na dokładność wy­znaczenia wielkości mierzonej, gdyż błędy pomiarów wielkości mierzonych bez­pośrednio przenoszą się w różny sposób na wynik końcowy.

W praktyce można spotkać się z przypadkiem, że wykonanie bezpośredniego pomiaru nie jest możliwe np. wyznaczenia gęstości ciała można dokonać tylko przez wyznaczenie jego masy i objętości. Niekiedy metodę bezpośrednią nazy­wamy metodą prostą,, a metodę pośrednią - metodą złożoną.

3.4. METODY PORÓWNAWCZE

Ze względu na sposoby porównania wartości wielkości mierzonych z wartościami wielkości wzorcowych rozróżnia się metody pomiarowe bez-

61

względne i porównawcze. Metody porównawcze, ze względu na zasadę porów­nania można podzielić na metodę odchyłową, metodę zerową i metodę różnico­wą. Metody zerowe, to metody kompensacyjne i metody komparacyjne.

Metoda pomiarowa bezwzględna jest to metoda pośrednia, w której równa­nie pomiaru jest równaniem definicyjnym tej wielkości. W metodzie bezwzględ­nej mierzy się te wielkości za pomocą których jest zdefiniowana wielkość mie­rzona. Do definicji najczęściej stosuje się wielkości podstawowe odtwarzalne najdokładniej. Przykładem tej metody może być pomiar pola prostokąta zdefi­niowanego jako iloczyn długości boków lub ciśnienie jako siła działająca na jed­nostkę powierzchni. W technice pomiarów elektrycznych metoda ta nie znajduje szerszego zastosowania.

Metoda pomiarowa porównawcza polega na porównaniu wartości wielkości mierzonej z inną wartością tej samej wielkości przyjętą za wartość wzorcową lub odniesienia. Może to być porównanie ze znaną wartością innej wielkości jako funkcji wielkości mierzonej. Można tu wyróżnić następujące metody:

Metoda odchyłową - wielkość mierzona jest przetwarzana w przyrządzie na taką samą wielkość jak wielkość wzorcowa. Przyrząd porównujący jest skalowa­ny w jednostkach wielkości mierzonej. Przyrządami porównującymi są przy­rządy elektromechaniczne. W przyrządach tych wielkość mierzona jest przetwo­rzona na moment napędowy, powodujący skręcenie organu ruchomego. Położe­nie organu ruchomego, a więc i wskazówki, jest funkcją wielkości mierzonej. Jest to metoda, która może być realizowana przy użyciu prostych środków tech­nicznych. Wadą natomiast jest stosunkowo mała, w porównaniu z innymi meto­dami, dokładność (0,1-5-0,5%). Przykładem stosowania tej metody jest pomiar natężenia prądu, pomiar napięcia miernikami elektromechanicznymi, a także po­miar masy wagą sprężynową uchylną.

Metoda zerowa polega na sprowadzeniu do zera różnicy AX między warto­ścią wielkości mierzonej X, a znaną, regulowaną wartością wielkości wzorcowej X_w. Miarą wartości A'jest w tej metodzie wartość X_w. Czynność badania różni­cy między Xi X_w i sprowadzenia jej do zera nazywamy procesem równoważe­nia. Proces ten jest realizowany za pośrednictwem detektora (wskaźnika ze­ra) i urządzenia wykonawczego regulującego wartość X_w w zależności od war­tości i znaku sygnału AX . Elementem wykonawczym może być w układach au­tomatycznych np. silnik nawrotny lub inne urządzenie elektryczne. W regulacji ręcznej rolę elementu wykonawczego spełnia obserwator. Stan obserwacji nie może być określony matematyczną równością X-X_W=AX=0, gdyż istnieje

nieskończenie wiele wartości \X - X_w\ < AX , dla których detektor przyjmuje ten sam stan. Jest to spowodowane skończoną czułością detektora.

62

Metoda zerowa może być realizowana jako metoda komparacyjna i metoda kom­pensacyjna.

Metoda komparacyjna - w tej metodzie można porównywać dwie różne wielkości. W tym celu należy obie lub tylko jedną z nich tak przetworzyć, aby reprezentowały jednakowe wielkości będące nośnikami energii, a następnie je skompensować. Analizując metodę kompensacji, z matematycznego punktu wi­dzenia, otrzymuje się, że wielkość mierzona X jest porównywana z wielkością wzorcową X _w za pomocą dodatkowego zbioru liczbowego k, który określa sto-X

sunek = k . Badając różnicę X - X_w • k sprowadza się ja do zera przez re-

X_w

gulację X_w. W miernictwie elektrycznym metodę komparacyjna wykorzystuje się do dokładnych pomiarów wartości skutecznej prądów lub napięć przemien­nych. Błąd tej metody można oszacować na ~ 0,05%.

Metoda kompensacyjna polega na tym, że w procesie porównania wielość mierzona jest przeciwstawiana wielkości wzorcowej tego samego rodzaju, która kompensuje jej fizyczne działanie na detektor. W stanie równowagi obie wielko­ści są jednakowe i skierowane przeciwnie (napięcie, prąd), X = X_w, i w tych wa­runkach detektor nie pobiera ze źródeł tych wielkości żadnej energii.

Metoda kompensacyjna charakteryzuje się następującymi cechami:

1. kompensację fizycznego działania wielkości można przeprowadzić
   tylko wtedy, gdy wielkość mierzona jest nośnikiem energii (rezystancji
   nie można bezpośrednio mierzyć metodą kompensacyjną),

2. w stanie równowagi (skompensowania) przyrząd nie pobiera żadnej
   energii z obiektu badanego; w stanie nieskompensowania w zależności
   czy wielkość kompensująca jest mniejsza czy większa od mierzonej, raz
   jest pobierana energia ze źródła wielkości mierzonej, drugi raz ze źródła
   wielkości wzorcowej.

Przykładem praktycznego zastosowania metody kompensacyjnej mogą być kom­pensatory prądowe i napięciowe lub waga dwuramienna mierząca na zasadzie kompensacji momentów.

Metoda różnicowa polega na porównaniu wartości wielkości mierzonej z niewiele różnicą się od niej znaną wartością X_w tej samej wielkości i następnie zmierzeniu różnicy tych wartości AX . Do pomiaru tej różnicy stosuje się najczę­ściej metodę odchyłową. Równanie pomiaru dla przypadku idealnego ma postać

X-X_W=AX (3.3)

a wielkość X_w jest nazywana wielkością porównawczą.

63

Przyrząd różnicowy ma większą dokładność niż przyrząd odchyłowy, gdyż łatwiej jest uzyskać błąd wielkości porównawczej mniejszy niż błąd przyrządu odchyłowego. Przy zachowaniu tej samej dokładności w przyrządzie różnicowym miernik może być mniej dokładny od przyrządu odchyłowego stosowanego w metodzie odchyłowej.

Przyrządy różnicowe są najczęściej stosowane do pomiaru bardziej złożo­nych wielkości fizycznych, których pomiar metodą odchyłową jest wykonywany z niewystarczającą dokładnością. Przykładem tej metody maja być mostki pracu­jące w stanie niezrównoważenia.

Ze względu na technikę porównania, metody pomiarowe można podzielić na metody realizowane przez podstawienie i metody realizowane przez przestawie­nie.

Metoda przez podstawienie - w metodzie tej wartość X wielkości mierzonej zastępuje się w układzie pomiarowym znaną wartością X _w tej samej wielkości, wybraną w ten sposób, aby skutki wywołane przez te dwie wartości były takie same. Wynik pomiaru wynosi wówczas X = X_w . Przykładem może być pomiar rezystancji omomierzem. Do zacisków wejściowych omomierza przyłączamy raz opornik badany, drugi raz opornik wzorcowy regulowany, którego wartość tak zmieniamy, aby wskazania miernika w obydwu przypadkach były takie same.

Metoda przez przestawienie - stosowana w metodach zerowych polega na porównaniu wartości wielkości mierzonej najpierw ze znaną wartością A tej wiel­kości, a następnie na przestawieniu wielkości mierzonej w miejsce A, i ponowne jej porównanie ze znana wartością B tej samej wielkości. Jeżeli w obydwu przy­padkach osiągnięto ten sam stan równowagi układu, to wówczas wartość wielko­ści mierzonej jest równa X = J A- B . Przykładem może być pomiar rezystancji mostkiem Wheatstone'a.

Jeżeli dla układu pomiarowego mostka Wheatstone'a stany równowagi wy­stąpią wtedy, gdy

X • /?2 ⁼ R ' R\ oraz

R"-R₂=X-R_l

to po przekształceniach uzyskuje się

Innym przykładem może być układ z wagą szalkową do pomiaru masy.

4

ANALIZA BŁĘDÓW POMIAROWYCH

4.1. PRZYCZYNY I RODZAJE BŁĘDÓW

Otrzymany na drodze doświadczalnej wynik pomiaru dowolnej wielkości fizycznej zawsze różni się od wartości rzeczywistej. Wartość rzeczywista jest pojęciem abstrakcyjnym i nie może być znana eksperymentatorowi. Pomiar po­zwala zatem na znalezienie przybliżonych wartości miar wielkości mierzonych.

Przyczynami rozbieżności między wynikiem pomiaru, a wartością rzeczywistą są:

1. ograniczona dokładność narzędzi pomiarowych,

2. niedokładność stosowanej metody pomiarowej,

3. niedoskonałość zmysłów obserwatora,

4. wpływ zmieniających się w czasie pomiaru wielkości wpływających.
   Niedokładność przyrządu. Składowa błędu podstawowego przyrządu jest

spowodowana niedoskonałością wykonania elementów składowych, nieidealno-ścią właściwości materiałów użytych do budowy przyrządu i niedokładnością wzorcowania. Dla użytkowych narzędzi pomiarowych wartości błędów podsta­wowych są podawane jako błędy graniczne dopuszczalne. Wyznaczają one naj­większą wartość błędu wskazania, jaka może wystąpić w dowolnym punkcie za­kresu pomiarowego przyrządu w przypadku jego poprawnego użytkowania w warunkach odniesienia. Przez warunki odniesienia przyrządów rozumie się ta­kie warunki, dla których podawane są dopuszczalne błędy przyrządu pomiarowe­go. Do najważniejszych parametrów charakteryzujących warunki odniesienia na­leży zaliczyć:

1. temperaturę,

2. ciśnienie,

3. wilgotność względną,

4. brak wstrząsów, wibracji i innych zakłóceń.

Warunki odniesienia dotyczą danego przyrządu (urządzenia) pomiarowego i powinny być podawane przez producentów.

Błędy metody są spowodowane przede wszystkim oddziaływaniem przyrzą­dów pomiarowych na wielkość mierzoną lub zjawisko będące źródłem tej wiel­kości. Przykładem może być przyłączenie woltomierza, który zmienia rozpływ

65

prądów w badanym obwodzie lub zainstalowanie termometru, co zmienia rozkład pola temperaturowego.

Poza tym do błędu metody zaliczyć można błędy spowodowane sprzężenia­mi galwanicznymi, indukcyjnymi, i pojemnościowymi występującymi miedzy elementami układu pomiarowego. Błędy te powinny być sprowadzone do warto­ści praktycznie pomijalnych w stosunku do wartości błędu podstawowego. Jeżeli jest to niemożliwe, należy zmienić metodę pomiaru lub wprowadzić do wyniku pomiaru poprawki eliminujące błąd metody.

Niedokładność zmysłów obserwatora powoduje powstanie błędów w takich przypadkach, w których ocenia się położenie wskazówki między dwiema sąsied­nimi kreskami podziałki, ocenia się natężenie dźwięku za pomocą słuchu, barwy lub równomierności oświetlenia całego pola widzenia za pomocą wzroku lub też w przypadku wykonywania w czasie pomiaru takich czynności, których jakość jest zależna od reakcji obserwatora.

Wartości czasu reakcji wynoszą średnio dla bodźców a) wzrokowych 0,15-*-0,2s, b) słuchowych O, l •*-(), 15s, i zależą w pewnym stopniu od natężenia bodźca jak i ogólnego stanu fizycznego obserwatora (np. zmęczenie fizyczne, psychiczne, itp.).

Obserwator może rozróżnić nieuzbrojonym okiem odległość punktów lub kresek wynoszącą 0,05+0, l mm. Odczytanie i zapamiętanie jednej cyfry jest możliwe, gdy ekspozycja obrazu trwa ponad O, l s; liczba trzycyfrowa wymaga już

czasu 0,3-5-0,5s. Jeżeli liczba ma więcej cyfr, to czas odczytywania znacznie wzra­sta.

Niekiedy w pomiarach słuch jest wykorzystywany do stwierdzenia zaniku dźwięku lub do porównania wysokości dźwięków. Zakres częstotliwości, na które reaguje ucho ludzkie wynosi od 16 do 20000Hz, przy czym największa czułość występuje w zakresie 200-5-5000 Hz. W przedziale największej czułości, granicz­na czułość ucha wynosi około 1-10"^I7W.

Błąd paralaksy jest związany z niedoskonałością zmysłów obserwatora i powstaje w skutek niewłaściwego kierunku rzutowania wskazówki na płytkę podziałkową. W celu wyeliminowania błędu paralaksy w przyrządach klas labo­ratoryjnych pod płytką podziałkową umieszcza się lusterko do kontroli kierunku patrzenia. Kierunek jest prawidłowy, gdy wskazówka pokrywa się z obrazem

wskazówki w lusterku. W przyrządach ze wskazówką świetlną ten błąd nie wy­stępuje.

Wpływ warunków odniesienia

Błędy spowodowane czynnikami wpływającymi mają najczęściej wartości zmienne w czasie. Wpływ tych błędów na wynik pomiaru jest odczuwalny przede wszystkim w pomiarach bardzo dokładnych.. W pomiarach techniczno-ruchowych, w których używane są mniej dokładne przyrządy, błędy spowodowa-

66

ne zmieniającymi się w czasie wielkościami wpływającymi mają mniejszy wpływ na końcowy wynik pomiaru.

Rodzaje błędów

Każdy wynik pomiaru różni się od wartości rzeczywistej. Różnicę między wartością W_t uzyskaną w wyniku /-tego pomiaru, a wartością rzeczywistą W_r na­zywamy błędem bezwzględnym prawdziwym

^=W_t-W_r (4.1)

Błąd ten może mieć znak dodatni lub ujemny. Występują jednak duże trud­ności z jego wyznaczeniem ze względu na to, że nieznana jest wartość rzeczywi­sta mierzonej wartości. W praktyce, zamiast wartości rzeczywistej przyjmuje się wartość poprawną W_p . Jest to wartość najbardziej zbliżona do rzeczywistej, wartość najbardziej prawdopodobna. Błąd ten nazywamy blędem poprawnym.

* = W_t-W„ (4.2)

W technice pomiarowej korzysta się często z tak zwanej poprawki, jest to taka wartość, którą należy dodać do wartości zmierzonej, aby otrzymać wartość poprawną

W_p=W_i+k (4.3)

Poprawka jest równa błędowi bezwzględnemu poprawnemu ze znakiem przeciwnym. Dla scharakteryzowania dokładności pomiarów wyznacza się błąd względny

5_% = ' ~ " 100 (4.4)

^% W_p

W praktyce często nie jest możliwe wyznaczenie błędu poprawnego i wprowa­dzenia korekty do wyniku pomiaru. W takim przypadku szacuje się granice prze­działu w otoczeniu mierzonej wartości, w którym będzie mieścić się wartość rze­czywista mierzonej wielkości. Stanowi to podstawę do wyznaczenia tak zwanego błędu granicznego &_g. Błąd graniczny wykorzystuje się najczęściej do oceny

dokładności przyrządów i urządzeń pomiarowych.

Ze względu na przyczyny występowania błędy w pomiarach można podzielić na:

- błędy systematyczne,

67

• błędy przypadkowe,

• błędy nadmierne, pomyłki.

Błędy systematyczne, to błędy, które przy wielu pomiarach wartości tej samej wielkości, wykonywane w tych samych warunkach, pozostają stałe co do wartości i znaku. Przykładem błędu systematycznego może być błąd wskazania miernika ana­logowego wynikający z nieprawidłowego wykreślenia podziałki. Błędy systema­tyczne powinny być w całości, lub częściowo, wyeliminowane z wyniku pomiaru.

Błędami przypadkowymi nazywamy błędy zmieniające się w sposób nie­przewidziany zarówno co do wartości jak i znaku przy wykonywaniu dużej licz­by pomiarów w warunkach praktycznie niezmiennych. Wyeliminowanie błędu przypadkowego nie jest możliwe. Wartość błędów przypadkowych wyznacza się korzystając z metod rachunku prawdopodobieństwa i statystyki matematycznej.

Błędy nadmierne powstają przy nieprawidłowym wykonywaniu pomiarów, wadliwym działaniu przyrządów lub niespodziewanym wystąpieniu nieznanych zjawisk. Przykładem może być powstanie błędu nadmiernego wskutek błędnego odczytu wskazania. Wynik pomiaru obarczony błędem nadmiernym jest niewia­rygodny i musi być usunięty z serii pomiarów.

Ocena dokładności uzyskanych w procesie pomiaru wyników może być przeprowadzona przy wykorzystaniu teorii błędów lub przy wykorzystaniu teorii niepewności.

Teoria błędów bazuje na modelu deterministycznym i losowym niedokład­ności. Wyznaczanie błędów może być realizowane przy przyjęciu modelu loso­wego metodą powtarzania błędów systematycznych, lub metodą randomizacji i centryzacji błędów systematycznych. Teoria ta, wydaje się, że może być stoso­wana do oceny dokładności przyrządów pomiarowych, w procesie oznaczania klasy ich dokładności.

Teoria niepewności przyjmuje za punkt wyjścia losowy model niedokładno­ści i hipotetyczne powtarzanie pomiaru prowadzące do nieobciążonej randomi-zowanej estymaty wielkości mierzonej. Stosowanie teorii niepewności do oceny wyniku pomiaru stało się obowiązujące dla służb związanych z miarami. Została ona przyjęta przez międzynarodowe organizacje metrologiczne i europejskie la­boratoria akredytowane. Trzeba ją znać i stosować wszędzie tam, gdzie wyma­gają tego przepisy.

Obliczanie błędu lub niepewności wyniku pomiaru jest procesem dość zło­żonym. Pełne poznanie teorii błędu i teorii niepewności wymaga zrozumienia ich istoty, co wymaga znajomości probabilistyki i statystyki matematycznej. Stoso­wanie analogii przy obliczaniu błędów czy niepewności często okazuje się bardzo zawodne.

68

4.2. TEORIA BŁĘDÓW

4.2.1. Błąd pomiaru bezpośredniego

Pomiar bezpośredni wykonuje się za pomocą przyrządu pomiarowego, któ­rego wskazanie y jest wartością mierzonej wielkości. Do oceny dokładności po­miaru przyjmuje się deterministyczny i losowy model błędu.

Model deterministyczny błędu pomiaru zakłada, że powtarzanie pomiaru daje zawsze takie same wartości obarczone zawsze takim samym błędem po­prawnym, nieznanym co do wartości. Jest to tak zwany błąd systematyczny. Moż­na w tym przypadku wyznaczyć tylko wartość graniczną błędu. Błąd graniczny jest równy połowie szerokości przedziału, największego jaki można ustalić wokół wartości oczekiwanej, w którym mieści się wartość prawdziwa. Błąd poprawny w stosunku do błędu granicznego zachowuje relacje

Wartość graniczną błędu wyznacza się dla danego przyrządu pomiarowego na podstawie jego klasy dokładności. Błąd graniczny dla przyrządów elektromecha­nicznych liczbowo jest równy wskaźnikowi klasy dokładności. Na przykład woltomierz klasy 0,5 i U„ = 100V charakteryzuje się błędem granicznym

względnym równym 0,5%, a błędem bezwzględnym At/ = 0,5 • 0,01 • t/„ = 0,5V . Model losowy błędu zakłada, że hipotetyczne powtarzanie pomiaru w wa­runkach powtarzalności prowadzi do randomizacji wartości oczekiwanej. Staje się ona zmienną losową, co pociąga za sobą randomizację błędu granicznego. Przedział niepewności staje się przedziałem losowym. Błąd ten nazywamy błę­dem przypadkowym. Błąd przypadkowy &_R- - średniej arytmetycznej równy jest średniej geome-

trycznej błędów przypadkowych pomiarów elementarnych. Błąd graniczny dla modelu losowego wyznacza się przez powtarzanie serii n pomiarów elementar­nych.

a_s/?? = Za(Xj)/-Jn dla rozkładu normalnego (n > 30)

^a«rx = ^łk_P ^s(^xi )/V" ^dla rozkładu ^-Studenta (4.5)

gdzie: tf(X) i S(X) odchylenie standardowe pojedynczego pomiaru i jej estymata,

69

Zp, tkp współczynnik rozkładu normalnego i rozkładu f-Studenta o (n -1) stopniach swobody wyznaczony dla poziomu ufności p.

(4.6)

M — l

(4.7) n-\

(4.8)

Błąd graniczny całkowity wyniku pomiaru, średniej arytmetycznej na poziomie ufności p oblicza się jako sumę algebraiczną granicznego błędu systematycznego i granicznego błędu na poziomie ufności p obliczonego z przyjętego modelu lo­sowego.

X (4.9)

Przyjmując rozkład losowy błędów, błąd graniczny jest równy pierwiastkowi z sumy kwadratów składowych błędów granicznych

(4.10)

Przykład 4.1

Obliczyć graniczny błąd pomiaru napięcia za pomocą woltomierza cyfrowego klasy 0,1 o zakresie znamionowym U „ =50V. Pomiar przeprowadzono dziesię­ciokrotnie uzyskując następujące wyniki pomiaru:

t/, = 25,03V U₆ = 25,01V

f/₂=25,05V f/₇=25,05V

f/₃=25,06V [/₈=25,02V

(7₄=24,98V f/₉=25,OOV

f/₅ = 24,93V f/₁₀ = 24,95V

70

Obliczenia błędu przeprowadzić dla rozkładu najmniej korzystnego i losowego rozkładu błędów.

Obliczenia

Wartość średnia napięcia

i ⁿ

= 25,00 +

0,03 + 0,05 + 0,06 - 0,02 - 0,07 + 0,01 + 0,05 + 0,02 + 0,0-0,05 _

10

= 25,008 = 25,0 IV Odchylenie standardowe pojedynczego pomiaru

n-l

Błędy pozorne

Zestawienie wyników obliczeń

/	ux	a; =!/,. -u,	(A;)^2xio-^6
1	25,03	+0,022	484
2	25,05	+0,042	1764
3	25,06	+0,052	2704
4	24,98	-0,028	784
5	24,93	-0,078	6084
6	25,01	+0,002	4
7	25,05	+0,042	1764
8	25,02	+0,012	144
9	25,00	-0,008	64
10	24,95	-0,058	3364
		S°	£ = 17160-10-*

Odchylenie standardowe pojedynczego pomiaru

71

Wartość graniczna błędu przypadkowego dla poziomu ufności p = l, k = 3

A _RU_X = kS_x = 3 -= = -. • 0,044 = 0,042V

= = -.L • n Vi O

Błąd graniczny systematyczny

A_gSt7, =8_g£/„ = 0,01-0,1-50 = 0,C

Błąd graniczny całkowity pomiaru napięcia, przy przyjęciu najgorszego rozkładu b_gU_x = &_gSU_x + tL_gRU_x = 0,05 + 0,042 = 0,092 = 0,09V

Błąd graniczny względny

6 ._T =-4^100 = ^^100 = 0,367% = 0,37%
^gu U_x 25,01

Błąd graniczny całkowity pomiaru napięcia przy przyjęciu losowego rozkładu błędów

a; U_x = ^²_gSU_x+A²_gKU_x = VO,05²+0,042² = 0,0652 » 0,07 V Błąd graniczny względny

₌

^8U U_x 25,01

4.2.2. Błąd pomiaru pośredniego

Wielkość mierzona jest funkcją wielu zmiennych, w celu wyznaczenia jej war­tości mierzy się bezpośrednio wartości kilku wielkości wejściowych X_l,X₂...X _N , a wartość mierzoną oblicza się z zależności funkcyjnej

72

Y = f(X_t,X₂...X_H) (4.11)

Jest to tak zwany pomiar pośredni. Funkcję f(X_r..X_N)nazywa się funkcją pomiaru.

Każda z wielkości wejściowych X, jest mierzona w warunkach powtarzalności n razy, w wyniku otrzymuje się następujące wartości:

dlaX, są to x_n,x_l2,...x_ln

dlaX, są to X_2l,x₂₂,...x_2a (4.12)

dlaX„ są to x_m,x_N2,...x_Nn

Uzyskane w wyniku pomiaru wartości X_l,X₂... X_N obarczone są błędami od­powiednio AX,, AX₂...AX_/V. Błędy te są funkcją błędów systematycznych i błę-

dów przypadkowych.

Wartość wielkości mierzonej dla pomiaru idealnego oblicza się z zależności funkcyjnej (4.11), dla warunków rzeczywistych funkcję tę można opisać nastę­pująco

)] (4.13)

Błąd pomiaru wielkości Obędzie w tych warunkach określony zależnością

^{Ay = ł}"-^{y =} (414)

Należy zatem określić w jaki sposób błędy wyznaczenia wielkości pośrednich X , , X₂ ... X _N przenoszą się na wynik pomiaru wielkości Y. Zależność miedzy błędem wyznaczenia wielkości Y a błędami AX,, AX₂,... &X_N wynika z prawa przenoszenia błędów.

Ze wzoru (4.15) w praktyce nie można korzystać, gdyż nie są znane błędy cząstkowe zarówno co do wartości, jak i znaku. Można jedynie wyznaczyć war­tości graniczne błędów. Dla wyznaczenia błędu A7 wielkości mierzonej przyj­muje się najmniej korzystny przypadek, w którym błędy wielkości pośrednich

73

jednocześnie przyjmują wartości graniczne i mają te same znaki. Wyznaczony w tych warunkach błąd nosi nazwę błędu granicznego.

^df A X	+ r	# A V		+ .. *,	•	^9/ A X
ax,^A«^XlV			dx N S ;=i			"s^z 2 df A			ax ' ^w ^CTA N
							<*/'

(4.16)

Wielkość

, jest pochodną cząstkową funkcji pomiaru względem zmien-

oX

nej X j , nazywa się współczynnikiem wrażliwości funkcji na zmiany wielkości wejściowej X . .

Błąd A _g X j _; , który jest błędem całkowitym granicznym wielkości zmierzonej

metodą bezpośrednią wyznacza się tak, jak podano w punkcie 4.2. l .

Błąd graniczny dla najczęściej występujących funkcji pomiaru wyznaczają następujące zależności

v —

¹ -

X

f — l

X,-X₂

= CX"

x

y z x

Wielkości pośrednie X,, X₂... X_N, wyznacza się przeprowadzając serie po­miarów. Na podstawie uzyskanych wyników określa się wartość średnią, błąd systematyczny i błąd przypadkowy.

74

Wartość wielkości zmierzonej można wyznaczyć korzystając z zależności funkcyjnej na wartości średnie

F = /(X„X₂...X„) (4.17)

lub wyznaczając wartości Y_l,Y₂...Y_N dla kolejnych wartości X_H, X₂₁ —X_Ni ... X_m,X_N2...X_Nn, a następnie obliczyć wartość średnią

(4.18)

Jeżeli funkcja pomiaru jest funkcją liniową, to uzyskane wartości Y wg wzo­rów 4.17 i 4.18 będą takie same. Sposób drugi obliczania wartości mierzonej nie może być stosowany, jeżeli poszczególne wielkości pośrednie X,, X₂... X_N byty mierzone w seriach o różnej liczności.

Przykład 4.2

W celu wyznaczenia w badanym obwodzie natężenia prądu zmierzono napięcie na zaciskach rezystora wzorcowego, włączonego do tego obwodu. Napięcie zmierzono 5-ciokrotnie woltomierzem cyfrowym o zakresie U_n = 100V, i rezy­stancji wejściowej R_v >10⁹Q, dla którego błąd określony przez producenta jest równy 0,05% wartości znamionowej. Uzyskano następujące wartości C/,. = (80,03; 80,05; 80,06; 79,95; 79,98)V . Rezystor wzorcowy R_n = 100Q, klasy dokładności 0,02. Obliczyć graniczny błąd pomiaru.

Rozwiązanie

Ze względu na dużą rezystancję wejściową woltomierza, można pominąć jego wpływ na rozpływ prądów. Wartość średnia pomiaru napięcia.

U_x = - V U, = - 400,07 = 80,014V »w 5

Odchylenie standardowe wartości średniej

75

5(5-1)

= 0,0211 = 0,02 V

U*_ ₌ 80,014 ₌ /?„ 100

_{800 lmA}

n	<//	(</,-",)	(o, -"J
1	80,03	0,016	2,56 -10"^4
2	80,05	0,036	12,96 -10-^4
3	80,06	0,046	21,16 -10"^4
4	79,95	-0,064	40,96-1 0"^4
5	79,98	-0,034	11,56-KT^4
	S	0	89,2 -10-^4

Błąd graniczny przypadkowy pomiaru napięcia dla k = 3

AjjŻ/, = 3 • 5^ = 3 • 0,0211 = 0,063V Błąd systematyczny graniczny woltomierza

&_gSU_x= 0,01 • 0,05 • 100 = 0,05V

Błąd graniczny całkowity pomiaru napięcia dla najniekorzystniejszego przypadku b_gU_x = &_gSU_x + b_gRV_x = 0,05 + 0,063 = 0,103V

Błąd graniczny opornika wzorcowego

A_x R„ = 0,01 • 0,02 • 100Q = 0,02Q

76

Korzystając z prawa przenoszenia błędów, błąd całkowity pomiaru natężenia prą­du

g *

A„/ =

du

*,v*

g n

-A„/?

—0,103 + -ir- • 80,01 • 0,02 = 0,103 • 10"² + 80,01 • 10~⁴ =
100 100²

= (0,103 + 0,8001)- 10~² =9,OmA

Wynik pomiaru

= /± A_g /,= (800,1 ±9,0)mA

4.2.3. Błędy nadmierne i ich wykrywanie

W serii przeprowadzonych pomiarów mogą występować wartości znacznie różniące się od innych. Mówimy wówczas, że wyniki te są błędne, to znaczy obarczone błędami nadmiernymi. Błędy te zaliczamy do grupy błędów przypad­kowych.

Jedną z głównych przyczyn występowania błędów nadmiernych jest nieuwa­ga mierzącego. Jeżeli wykonujemy tylko jeden pomiar, to ujawnienie tego błędu nie jest możliwe. Tylko wykonanie serii pomiarów pozwala na ujawnienie tych błędów. Istnieje wiele metod statystycznych pozwalających na ujawnienie, a tym samym na eliminację błędów nadmiernych. Można przyjąć, że błędy dla których prawdopodobieństwo wystąpienia jest mniejsze od pewnej założonej wartości np. p < P są pomyłkami. Przy określaniu wartości P posługujemy się często odchy­leniem standardowym.

Jedną z prostszych metod wykrywania błędów nadmiernych jest metoda po­legająca na przyjęciu, że p przyjmuje wartość prawdopodobieństwa odpowiada­jącego potrójnej wartości odchylenia standardowego. Oznacza to, że prawdopo­dobieństwo pojawienia się błędu większego od 35 jest mniejsze od 0,003. Moż­na zatem uważać, że jeżeli w serii wyników pomiarów znajdzie się wynik różnią­cy się od wartości średniej więcej niż o 35, to jest on prawdopodobnie spowo­dowany pomyłką.

Inną metodą jest metoda polegająca na określeniu, czy wynik budzący wąt­pliwości mieści się z założonym prawdopodobieństwem w określonym przedzia­le. Otrzymane w serii wyniki pomiarów porządkujemy według rosnących warto­ści, od wartości najmniejszej X_{ do największej X_n. Odrzucamy wynik budzący

77

wątpliwość, może to być wynik najmniejszy lub największy. Dla pozostałych w serii wyników pomiarów o liczności n = n - 1 oblicza się wartość średnią i odchylenie standardowe pojedynczego pomiaru i odchylenie standardowe dla średniej.

n -l
$
oraz st

Przy próbie mało licznej (n < 30) dla założonego prawdopodobieństwa p oraz wynikającej z pomiaru liczby stopni swobody k = n' -1, wyznacza się z tablic rozkładu Studenta współczynnik t^. Następnie wyznacza się przedział, w któ­rym może występować wartość poprawna mierzonej wielkości.

X-t_kpS<X<X+t_kpS

Jeżeli podejrzany wynik X, lub X_n nie mieści się w wyznaczonym prze­dziale [17] odrzucamy go przyjmując, że jest on obarczony błędem nadmiernym.

Przykład 4.3

W wyniku dwunastokrotnego pomiaru napięcia U otrzymano następujące wyniki X,= (1,022; 1,023; 1,024; 1,024; 1,025; 1,025; 1,025; 1,026; 1,026; 1,027; 1,028; 1,053)V. Sprawdzić metodą 3S i metodą przedziału, czy któryś z wyników po­miaru nie jest obarczony błędem nadmiernym. Obliczenia przeprowadzić dla p = 0,99.

Rozwiązanie

Wartość średnia

t/=J=L_ = lł328=i,027V
n 12

Wyniki dalszych obliczeń przedstawiono w tabeli

78

n	u,	U, -U	(U i -U J -HT^6	U, -U'	(j/,.- u 'J -10^
	V	V	V^2	V	v^2
1	,022	- 0,005	25	-0,003	9
2	,023	-0,004	16	-0,002	4
3	,024	- 0,003	9	-0,001	1
4	,024	- 0,003	9	-0,001	1
5	,025	- 0,002	4	0,00	0
6	,025	- 0,002	4	0,00	0
7	1,025	- 0,002	4	0,00	0
8	1,026	- 0,001	1	0,001	1
9	1,026	- 0,001	1	0,001	1
10	1,027	0,00	0	0,002	4
11	1,028	0,001	1	0,03	9
12	1,053	0,026	476	-	-
S	12,328	0	750	0	30

Odchylenie standardowe pojedynczego wyniku pomiaru

= 0,008V

Stosujemy kryterium 35.

Wartość 35 = 3 • 0,008 = 0,024 V

Z porównania wyników okazuje się, że wynik pomiaru 12 obarczony jest błędem przekraczającym wartość 35 (0,026 > 0,024). Wynik ten należy uznać za błędny.

Metoda wyznaczania podziału.

Z otrzymanych wartości wynik 12 budzi wątpliwości co do swojej wiarygodno­ści. Zostaje on pominięty w obliczeniach. Obliczamy średnią na «' = n-l = 12-l = ll pomiarów

U' = -

11,275 11

= 1.025Y

Odchylenie standardowe pojedynczego pomiaru

79

S' = \|-ts!—. ₌ I^J" ^tv/ - o,0017 « 0,002V

Dla poziomu ufności p = 0,99 i punktów swobody n-l = ll-l = 10 z tablic rozkładu Studenta znajdujemy współczynnik t^ = 3,169. Stąd

t_kpS = 3,169-0,002 = 0,00634 » 0,006V

Dla U = 1,025V otrzymuje się przedział

1,025 - 0,006 < U < 1,025 + 0,006 l,019V<f/<l,031V z prawdopodobieństwem p = 0,99.

Znacznie różniąca się wartość U₁₂ = 1,053V, nie mieści się w wyznaczonym

przedziale. Powinna zostać pominięta w dalszej analizie jako wartość obarczona błędem nadmiernym.

5

NIEPEWNOŚCI WYNIKU POMIARU

5.1. PODSTAWY TEORII NIEPEWNOŚCI

Teoria niepewności przyjmuje losowy model niedokładności zakładając, że wartość oczekiwana X, estymata wielkości mierzonej e(x) jest jedną z wartości zmiennej losowej X o wartościach danych przez hipotetyczne doświadczenie po­zyskiwania estymaty X. Niedokładność pomiaru charakteryzuje się w tym przy­padku za pomocą parametru zwanego niepewnością. Niepewność w [3] definio­wana jest jako parametr związany z wynikiem pomiaru charakteryzujący rozrzut wartości, które można w uzasadniony sposób przypisać wartości mierzonej. Takim parametrem może być na przykład odchylenie standardowe (lub jego wielokrotność), albo połowa szerokości przedziału odpowiadającego określone­mu poziomowi ufności. Niepewność pomiaru zawiera na ogół wiele składników. Niektóre z nich można wyznaczyć na podstawie rozkładu statystycznego wyni­ków szeregu pomiarów i można je scharakteryzować odchyleniem standardo­wym. Inne składniki pochodzące na przykład od efektów systematycznych są szacowane na podstawie zakładanych rozkładów prawdopodobieństwa opartych na posiadanym doświadczeniu lub uzyskiwanych z innych źródeł.

Niedokładność pomiaru charakteryzuje się przez podanie niepewności stan­dardowej, niepewności łącznej i niepewności rozszerzonej.

Niepewność standardowa u(x) wyrażana jest przez odchylenie standardowe wyników szeregu pomiarów wykonywanych w niezmiennych warunkach odnie­sienia.

u(x) = S (5.1)

Niepewność złożona (łączna), to niepewność standardowa wyniku pomiaru otrzymanego na podstawie pomiaru kilku wielkości, równa pierwiastkowi kwa­dratowemu z sumy składników będących wariancjami i kowariancjami tych wielkości pomnożonymi przez odpowiednie współczynniki zależne od funkcji pomiaru

81

(5.2)

Tabela 5.1

t\«D	0	1	2	3	4	5	6	7	8	9
0,0 i	0,00000 03983	0,00399 04380	0,00798 04776	0,01197 05172	0,01595 05567	0,01994 05962	0,02392 06356	0,02790 06749	0,03188 07142	0,03586 07535
2	07926	0,8317	08706	09095	09483	09871	10257	10642	11026	11400
3	11791	12172	12552	12930	13307	13683	14058	14431	14803	15173
4	15542	15910	16276	16640	17003	17364	17724	18082	18439	18793
0,5	0,19146	0,19497	0,19847	0,20194	0,20540	0,20884	0,21226	0,21566	0,21904	0,22240
6	22575	22907	23237	23565	23891	24215	24537	24857	25175	25490
7	25804	26115	26424	26730	27035	27337	27637	27935	28230	28524
8	28814	29103	29389	29673	29955	30234	30511	30785	31057	31327
9	31594	31859	32121	32381	32639	32894	33147	33398	32646	33891
1,0	34134	34375	34614	34850	35083	35314	35543	35769	35993	36214
1	36433	36650	36864	37076	37286	37493	37698	37900	38100	38298
2	38493	38686	38877	39065	39251	39435	39617	39796	39973	40147
3	40320	40490	40658	40824	40988	41149	41309	41466	41621	41774
4	41924	42073	42220	42364	42507	42647	42786	42922	43056	41389
5	43319	43448	43574	43699	43822	43943	44062	44179	44295	44408
6	44520	44630	44738	44845	44950	45053	45154	45254	45352	45449
7	45543	45637	45728	45818	45907	45994	46080	46164	46246	46327
8	46407	46485	46562	46638	46712	46784	46856	46926	46995	47062
9	47128	47193	47257	47320	47381	47441	47500	47558	47615	47670
2,0	47725	47778	47831	47882	47932	47982	48030	48077	48124	48169
1	48214	48257	48300	48341	48382	48422	48461	48500	48537	48574
2	48610	48645	48679	48713	48745	48778	48809	48840	48870	48899
3	48928	48956	48983	49010	49036	49061	49086	49111	49134	49158
4	49180	49202	49224	49245	49266	49286	49305	49324	49343	49361
2,5	49379	49396	49413	49430	49446	49461	49477	49492	49506	49520
6	49534	49547	49560	49573	49586	49598	49609	49621	49632	49643
7	49653	49664	49674	49683	49693	49702	49711	49720	49728	49737
8	49745	49752	49760	49767	49774	49781	49788	49795	49801	49807
9	49813	49819	49825	49831	49836	49841	49846	49851	49856	49861
3,0	49865	49869	49874	49878	49882	49886	49889	49893	49897	49900
1	49903	49906	49910	49913	49916	49918	49921	49924	49926	49929
2	49931	49934	49936	49938	49940	49942	49944	49946	49948	49950
3	49952	49953	49955	49957	49958	49960	49961	49962	49964	49965
4	49966	49968	49969	49970	49971	49972	49973	49974	49975	49976
5	49977	49978	49978	49979	49980	49981	49981	49982	49983	49983
6	49984	49985	49985	49986	49986	49987	49987	49988	49988	49989
7	49989	49990	49990	49990	49991	49991	49992	49992	49992	49992
8	49993	49993	49993	49994	49994	49994	49994	49995	49995	49995
9	49995	49995	49996	49996	49996	49996	49996	49996	49997	49997

82

Niepewność rozszerzona, to wielkość określająca przedział wartości wokół wyniku pomiaru, jest ona równa iloczynowi niepewności złożonej i współczynni­ka rozszerzenia k

U = ku,(y) (5.3)

Współczynnik rozszerzenia zależy od przyjętego poziomu ufności i rozkładu zmiennej losowej x. W przypadku, gdy współczynnik k jest powiązany z pozio­mem ufności p to zapisuje się go jako k_p i wtedy niepewność rozszerzona jest

oznaczona przez U _p i wynosi

U=k_pu,(y) (5.4)

Tabela 5.2

Rozkład f-Studenta o k stopniach swobody

Liczba stopni swobody k	Poziom ufności
		68,27	90	95	95,45	99	99,73
1	1,84	6,31	12,71	13,97	63,66	235,80
2	1,32	2,92	4,30	4,53	9,92	19,21
3	1,20	2,35	3,18	3,31	5,84	9,22
4	1,14	2,13	2,78	2,87	4,60	6,62
5	1,11	2,02	2,57	2,65	4,03	5,51
6	1,09	1,94	2,45	2,52	3,71	4,90
7	1,08	1,89	2,36	2,43	3,50	4,53
8	1,07	1,86	2,31	2,37	3,36	4,28
9	1,06	1,83	2,26	2,32	3,25	4,09
10	1,05	1,81	2,23	2,28	3,17	3,96
11	1,05	1,80	2,20	2,25	3,11	3,85
12	1,04	1,78	2,18	2,23	3,05	3,76
13	1,04	1,77	2,16	2,21	3,01	3,69
14	1,04	1,76	2,14	2,20	2,98	3,64
15	1,03	1,75	2,13	2,18	2,95	3,59
16	1,03	1,75	2,12	2,17	2,92	3,54
17	1,03	1,74	2,11	2,16	2,90	3,51
18	1,03	1,73	2,10	2,15	2,88	3,48
19	1,03	1,73	2,09	2,14	2,86	3,45
20	1,03	1,72	2,09	2,13	2,85	3,42
25	1,02	1,71	2,06	2,11	2,79	3,33
30	1,02	1,70	2,04	2,09	2,75	3,27
35	1,01	1,70	2,03	2,07	2,72	3,23
40	1,01	1,68	2,02	2,06	2,70	3,20
45	1,01	1,68	2,01	2,06	2,69	3,18
50	1,01	1,68	2,01	2,05	2,68	3,16
100	1,005	1,660	1,984	2,025	2,626	3,077
oo	1,000	1,645	1,960	2,000	2,576	3,000

83

Jeżeli zmienna x ma rozkład normalny, to współczynnik rozszerzenia, dla określonego poziomu ufności, jako współczynnik z_a wyznacza się z tablic staty­stycznych rozkładu normalnego (tabela 5.1). Przy niezbyt licznej próbie (mała liczba wyników pomiaru, n< 30) rozkład normalny zastępuje się rozkładem Stu­denta. W tym przypadku współczynnik rozszerzenia przyjmuje wartości współ­czynnika rozkładu ^-Studenta dla określonej liczby stopni swobody równej liczbie pomiarów pomniejszonej o jeden i określonego poziomu ufności (tabela 5.2).

Jeżeli są trudności z wyznaczeniem współczynnika rozszerzenia dla zaist­niałych warunków pomiarowych, to zwykle przyjmuje się k_p = 3 i przypisuje się

mu poziom ufności p = 0,99 lub k_p =2 i przypisuje się mu poziom ufności p = 0,95.

Niepewność pomiaru może zawierać wiele składowych jak np. niepełna definicja wielkości mierzonej, niedoskonała realizacja definicji wielkości mierzonej, sposób pobierania próbek wielkości mierzonej, wpływ czynników zewnętrznych, rozdzielczość przyrządów pomiarowych, przybliżenia i założenia wynikające z metody pomiarowej, niedokładność wzorców.

Niektóre z tych niepewności można wyznaczyć na podstawie otrzymanego rozrzutu wyników serii pomiarów i inne, które ocenia się na podstawie przewi­dywanych rozkładów prawdopodobieństwa.

Te dwie, różne pod względem sposobu otrzymywania grupy niepewności, stanowią podstawę do podziału niepewności na dwa typy:

niepewności typu A, wyznaczane metodami statystycznymi, niepewności typu B, wyznaczane innymi metodami.

Niepewność typu A, ze względu na źródła jej powstawania można przyjąć, że odpowiada błędom spowodowanym efektami przypadkowymi, natomiast nie­pewność typu B odpowiada błędom spowodowanym efektami systematycznymi. Przy analizie niepewności pomiaru, typu A i typu B, zakłada się, że wszystkie znane poprawki zostały uwzględnione w wyniku pomiaru. Każda niepewność systematyczna o znanej wartości i znaku musi być uwzględniona w postaci po­prawki, jeżeli nie jest znana jej wartość, musi być traktowana jako niepewność dodatkowa. Niepewność ta ma charakter losowy. Należy ocenić miarę liczbową tej niepewności, którą jest odchylenie standardowe. Jeżeli niepewność ta jest wywołana przez efekty systematyczne, której najczęstszym źródłem jest błąd apa­ratury pomiarowej, to wartość graniczna A_? tego błędu umożliwia wyznaczenie

wariancji dla przyjętego rozkładu prawdopodobieństwa.

84

5.2. PRAWO PROPAGACJI NIEPEWNOŚCI

W pomiarach pośrednich mierzona wielkość jest funkcją wielu zmiennych Jeżeli funkcja pomiaru jest liniowa, to zmienne X_y są zmiennymi losowymi

o wartościach średnich odpowiednio X_jt a średnia mierzonej wielkości Y jest funkcją zmiennych X_y

(5.5)

Każda z wielkości Xj wyznaczona jest z niepewnością standardową s(Xj) lub niepewnością łączną M_T(*_y). Jeżeli wielkości Xj są nieskorelowane, wówczas niepewność u_T(y) mierzonej wielkości określona jest zależnością

(5.6)

W odniesieniu do wartości średnich wartość niepewności wyraża zależność

(5.7)

Gdy funkcja pomiaru charakteryzuje się znaczną nieliniowością wówczas przy rozwinięciu jej w szereg Taylora należy uwzględnić wyrazy wyższego rzę­du. Najważniejszymi wyrazami wyższych rzędów są

N N

ZE

a²/ l , a/ a³/

u²(x_i)u²(x_j) (5.8)

Wyrazy te powinny być uwzględnione przy obliczaniu niepewności łącznej.

Jeżeli wielkości pośrednie X_t,X₂ ... X_N są ze sobą skorelowane, występuje między nimi zależność funkcyjna, to oprócz obliczenia wariancji, dla wyznaczę-

85

nią niepewności trzeba także wyznaczyć kowariancję i wówczas niepewność łączna będzie określona wzorem

w którym: .k,-,*,- są oszacowaniami wartości wielkości X, i X_;,

-^—,—ł— są pochodnymi cząstkowymi funkcji pomiaru względem X i X ,,

^y

u(xj , *; ) jest kowariancją je, i x j .

Kowariancje u(x_i,x_j ) oblicza się ze wzoru

"v" t=i

w którym X_ilc,X_jk są A:-tym wynikiem bezpośredniego pomiaru wielkości X-, lub X_y. .

Dla oceny stopnia zależności miedzy poszczególnymi wielkościami X_t i X_;. wyznacza się współczynnik korelacji

u(x ,jc

Wyznaczona kowariancja m(jc,.;jc_;) jest równa kowariancji średnich ^(jć,;3ć_; i wówczas wzór 5. 1 1 przyjmuje postać

(5-12)

Jeżeli O < r < l , to jest to korelacja dodatnia, dla - 1 < r < O mamy do czy­nienia z korelacją ujemną. Im większa wartość r, tym większa zależność między X, i X_y,przy r = O , wielkości te nie są skorelowane.

86

Jeżeli znany jest współczynnik korelacji, to estymator konwariancji przy dwóch wielkościach oblicza się ze wzoru

";,ą =u_M-u_A2-r(x„x₂) (5.13)

Wielkości u_m i u_A2 oznaczają niepewności typu A dla wielkości X,,X₂.

5.3. OCENA NIEPEWNOŚCI W POMIARACH BEZPOŚREDNICH

5.3.1. Ocena niepewności typu A

W pomiarach bezpośrednich mogą występować niepewności typu A i nie­pewności typu B. Zostanie rozpatrzony przypadek, gdy niepewność typu A jest dużo większa od niepewności typu B.

u_a»u_b (5.14)

W praktyce można uznać, że spełniony jest warunek u_a » u_b , jeżeli u_B<0,lu_A.

Niepewność standardową typu A ocenia się za pomocą metod statystycz­nych. Na podstawie serii pomiarów oblicza się wartość średnią

_i (5.15)

"w

oraz niepewność standardową typu A

E (*,-*)

Przyjmuje się, że w wynikach pomiarów zostały uwzględnione wszystkie po­prawki.

87

Ponieważ występuje tylko jedna niepewność u_a , to niepewność łączna jest równa tej niepewności

"b =«a (5-17)

M_T =TU

Niepewność rozszerzona jest równa niepewności łącznej pomnożonej przez współczynnik rozszerzenia k_p.

U = k_au, (5.18)

Współczynnik rozszerzenia, przy dużej liczbie pomiarów, gdy można uwa­żać, że rozkład zmiennej losowej Xjest rozkładem normalnym, przyjmuje warto­ści zmiennej standaryzowanej Z dla tego układu.

Wartości zmiennej Z odczytuje się z tablic rozkładu normalnego dla określo­nego poziomu ufności p. Najczęściej stosowane wartości zmiennej Z dla określo­nego poziomu ufności p przedstawiono w tabeli 5.3.

Vybrane wartości współczynnika Z dla rozkładu normalnego Tabela 5.3
P	0,6827	0,900	0,950	0,9545	0,990	0,9973
Z	1,000	1,645	1,96	2,000	2,576	3,000

Dla innych wartości poziomu ufności współczynnik Z można wyznaczyć ko­rzystając z tabeli 5.1.

Jeżeli liczba pomiarów nie jest zbyt duża n < 30, to współczynnik rozsze­rzenia przyjmuje wartość zmiennej standaryzowanej rozkładu f-Studenta. War­tość tego współczynnika odczytuje się z tablic rozkładu Studenta dla założonego poziomu ufności p i dla liczby stopni swobody równej k = n -1. Dla przypadku, gdy rozkład zmiennej losowej nie może być uznany za rozkład normalny, ani za rozkład f-Studenta, to przyjmuje się arbitralnie współczynnik rozszerzenia równy 2 lub 3 uznając, że tym wartościom odpowiadają poziomy ufności p odpowiednio równe 0,95 i 0,99.

Przykład 5.1

Woltomierzem cyfrowym o napięciu znamionowym 100V i błędzie granicznym równym A_g = 0,0217,, +0,01f/_n, zmierzono sześciokrotnie napięcie. Otrzymano

następujące wartości: U_t = (80,42; 80,92; 80,31; 80,02; 80,56; 80,96)V. Obliczyć niepewność pomiaru napięcia na poziomie ufności p = 0,95.

88

Rozwiązanie

Wartość średnia mierzonego napięcia

«/=-!>,=

"w

483,19 6

= 80,53V

Tabelaryczne przedstawienie wyników obliczeń

n	tf,	fr -U)	fo-zry
	V	V	V^2
1	80,42	-0,11	0,0121
2	80,92	0,39	0,1521
3	80,31	-0,22	0,0484
4	80,02	-0,57	0,2601
5	80,56	0,03	0,0009
6	80,96	0,43	0,1849
S	483,19	0	0,6585

Niepewność standardowa typu A

= 0,148 IV

Sprawdzamy, czy niepewność typu A jest niepewnością dominującą. W tym celu wyznacza się niepewność typu B wnoszona przez woltomierz. Zakładając, że rozkład prawdopodobieństwa błędu miernika jest rozkładem równomiernym, nie­pewność standardowa typu B będzie równa

mb =•

d = ^(0,02-80,53+ 0,01-100) = 0,0150V

Ponieważ niepewność m_A= 0,148IV jest znacznie większa od niepewności u_b =0,0150V, to można uznać, że u_a jest niepewnością dominującą i w obli­czeniach można pominąć niepewność u_b .

89

Niepewność łączna pomiaru napięcia będzie równa

Liczba pomiarów jest mało liczna n = 6 , to dla obliczenia niepewności roz­szerzonej na poziomie ufności p = 0,95 należy wyznaczyć współczynnik t _kp dla

rozkładu Studenta. Liczba stopni swobody k = n - 1 = 5 .

Z tablic rozkładu Studenta dla p = 0,95 i k = 5 współczynnik t_kp = 2,57 .

Niepewność rozszerzona pomiaru napięcia

U_f = k_pu^ = r^M_t = 2,57 • 0,1481 = 0,3806V = 0,39V

Wynik pomiaru napięcia można zapisać następująco

U_x=U±U_p= (80,53 ± 0,39) V

5.3.2. Ocena niepewności typu B

W pomiarach wykonywanych w warunkach przemysłowych, gdy stosuje się aparaturę pomiarową mniej dokładną może wystąpić przypadek, gdy niepewność typu A jest dużo mniejsza od niepewności typu B tj. u_a < 0,1 u_g . Oznacza to, że

dominującą niepewnością jest niepewność typu B. Jest to niepewność wywołana przez efekty systematyczne, a jej źródłem jest niedokładność aparatury pomiaro­wej. Niepewność standardową typu B można ocenić w zależności od posiadanych informacji, takich jak np.:

właściwości przyrządów i metod pomiarowych,

danych kalibracyjnych przyrządu,

informacji podanych przez producenta,

danych z wcześniejszych pomiarów.

Dla danej wielkości przyporządkowuje się określony rozkład prawdopodo­bieństwa i oblicza odchylenie standardowe. W praktyce najczęściej mamy do czynienia z sytuacją obliczania niepewności typu B wynikającej z błędów apara­tury pomiarowej. Stosowaną aparaturę pomiarową charakteryzuje się za pomocą wartości błędu granicznego określonego przez wskaźnik klasy dokładności. Roz­kład błędów aparatury pomiarowej może być różnorodny, najczęściej jest to roz­kład jednostajny, rzadziej rozkład trójkątny.

90

-A.

Rys.5.1. Rozkład jednostajny i trójkątny

Dla rozkładu jednostajnego i trójkątnego wariancję i odchylenie standardowe określają zależności

Niepewność łączna dla tego przypadku m_t = u_b . Niepewność rozszerzoną wyznacza się ze wzoru

(5.20)

Dla rozkładu jednostajnego współczynnik rozszerzenia, w zależności od poziomu ufności, będzie miał wartość

k_p=j3-p (5.21)

Dla p = l, k_p - >/3 niepewność rozszerzona jest równa błędowi granicznemu U _p = A_g . Jest to najczęściej spotykany w praktyce przypadek.

Przykład 5.2

Woltomierzem magnetoelektrycznym klasy 0,5 o zakresie znamionowym 100V zmierzono napięcie uzyskując wynik U_x = 80,2V. Obliczyć niepewność pomiaru na poziomie ufności p - 0,95.

Rozwiązanie

Przyjmując, że rozkład prawdopodobieństwa błędu miernika jest rozkładem rów­nomiernym, niepewność standardowa typu B będzie równa

91

,*>iy..Ml.M.|flO.

Niepewność typu B jest niepewnością dominującą, niepewność typu A jest pomijalnie mała.

Niepewność łączna jest równa niepewności standardowej m_t = u_b . Niepewność rozszerzona

Współczynnik rozszerzenia, dla jednostajnego rozkładu błędów miernika dla po­ziomu ufności p oblicza się ze wzoru

Jt_p=VŚp = V3- 0,95 = 1,645

Stąd niepewność rozszerzona

U_f = k_pu_T = 1,645 • 0,289 = 0,475 » 0,5V

Wynik pomiaru napięcia

U_x=U±U_p=8Q,2V±0,5V

5.3.3. Ocena niepewności typu A i B

W praktyce najczęściej występuje przypadek, gdy niepewności typu A mają rozkład bliski rozkładowi normalnemu, a niepewności typu B są spowodowane przez błędy aparatury pomiarowej o rozkładzie równomiernym.

Niepewności typu A i B wyznacza się tak, jak to podano w punkcie 5.3.1 i 5.3.2. Znając wartości tych niepewności wyznacza się niepewność łączną.

+ " (⁵-²²)

Niepewność rozszerzoną określa zależność

92

Współczynnik rozszerzenia k_p ma wartość zależną od przyjętego poziomu

ufności oraz rozkładu wypadkowego wynikającego ze złożenia rozkładu normal­nego (niepewność typu A) i rozkładu jednostajnego (niepewność typu B).

Rozkład wynikający ze złożenia rozkładu normalnego i rozkładu jednostaj­nego opisany jest splotem tych rozkładów. Wyznaczenie splotów rozkładu nor­malnego i jednostajnego stwarza wiele problemów. W praktyce stosuje się różne metody przybliżone umożliwiające wyznaczenie współczynnika rozszerzenia.

Jedną z tych metod jest metoda oparta na hipotezie, że nieznany splot rozkła­dów składowych jest zbieżny do rozkładu składowego o większym odchyleniu standardowym. Gdy S_N > Sj , to splot rozkładu normalnego i jednostajnego jest zbieżny do rozkładu normalnego. Współczynnik rozszerzenia przyjmuje wówczas wartości zmiennej standaryzowanej Z rozkładu normalnego, dla określonego poziomu ufności.

Jeżeli S_N <Sj, odchylenie standardowe rozkładu normalnego jest mniejsze od odchylenia standardowego rozkładu jednostajnego, to splot rozkładów nor­malnego i jednostajnego jest zbieżny do rozkładu jednostajnego. Współczynnik rozszerzenia przyjmuje wówczas wartości zmiennej standaryzowanej rozkładu jednostajnego k_}.

Niepewność rozszerzoną określa zależność

l/=Mt (5-24)

Dla S_N ~ S j ocena niepewności rozszerzonej jest niejednoznaczna, zaleca się

w tym przypadku przyjęcie współczynnika rozszerzenia takiego, jak dla rozkładu normalnego.

Przykład 5.3

Watomierzem elektrodynamicznym klasy dokładności 0,2; P_n = 500W; U_n = 100V ; /„ = 5A zmierzono moc odbiornika przy prądzie stałym w układzie

o zadanym napięciu. Pomiar wykonano pięciokrotnie. Uzyskano następujące wartości: P = (358,1; 358,4; 357,8; 357,5; 357,5)W.

Rezystancja obwodu napięciowego watomierza R_wn = 10000Q, rezystancja wol­tomierza R_v >10⁹Q. Wyznaczyć niepewność wyniku pomiaru na poziomie ufności p = 0,95.

93

Rozwiązanie

Ze wskazań watomierza nie wynika, aby któryś wynik był obarczony błędem nadmiernym.

Wartość średnia pomiaru mocy

» w

1790,3

= 358,06 W

Zestawienie wyników obliczeń

n	p,	ti-f)	k -n
	w	W	w^2
1	358,1	0,04	0,0016
2	358,4	0,34	0,1156
3	357,8	-0,26	0,0676
4	357,5	-0,56	0,3136
5	358,5	0,44	0,1936
E	1790,3	0	0,692

Niepewność standardowa typu A

n(n-l) \ 5(5-1)

= 0,186 W

Niepewność standardowa typu B. Rozkład jednostajny błędów watomierza. 0,01- S_g-P_n 0,01-0,2-500

M„ =-

• = 0,577 W

Niepewność typu A i B są tego samego rzędu. Niepewność łączna

+0.577² =0,606W

94

Niepewność typu B, rozkład jednostajny, jest większa od niepewności typu A, rozkład normalny. Współczynnik rozszerzenia w tym przypadku zostaje przyjęty, tak jak dla rozkładu jednostajnego.

)t _p=V3-p = V3- 0,95 = 1,645

Niepewność rozszerzona

U_p=k_p-u^= 1,645 • 0,606 = 0,997 » 1,OW

Poprawka do wyniku pomiaru wynikającego z mocy pobranej przez obwód na­pięciowy watomierza

²

R 10000 Moc odbiornika

P₀=P_w-P_m,= 358,1 - 1,0 = 357.1W Wynik pomiaru

P = P±U_p= 357,1W ± 1,OW

5.4. OCENA NIEPEWNOŚCI W POMIARACH POŚREDNICH

5.4.1. Ocena niepewności typu A

W pomiarach pośrednich, jak to przedstawiono w punkcie 5.1, wielkość mie­rzona 7 jest funkcją wielkości X j mierzonych bezpośrednio. Każda z wielkości

X j jest wyznaczana na podstawie serii pomiarów, z których oblicza się wartość

średnią i niepewność standardową dla średniej Y .

Rozpatrywany jest przypadek, w którym niepewność typu A jest niepewno­ścią dominującą, to znaczy u_a »u_b, podobnie jak w punkcie 5.3. l.

Wartość wielkości mierzonej wyznacza się ze wzoru

F = /(*,) (5.25)

95

a niepewność standardową dla średniej Y, dla przypadku, gdy funkcja Y = f (X j) jest praktycznie liniowa, z zależności

<⁵-²⁶'

Przy dużej nieliniowości funkcji pomiaru, należy uwzględnić wyrazy wyż­szego rzędu w szeregu Taylora (zależność 5.8). Jeżeli zmienne losowe są wza­jemnie zależne, to należy obliczyć kowariancję według zależności (5.9).

Niepewność łączna, ponieważ występuje tylko niepewność typu A, jest rów­na tej niepewności u_r = u_aj .

Dla oceny niepewności rozszerzonej trzeba wyznaczyć współczynnik rozsze­rzenia, jego wartość, jak już uprzednio podano, jest zależna od przyjętego pozio­mu ufności i rozkładu prawdopodobieństwa wielkości Y . Rozkład ten jest splo­tem rozkładów Xj . Wyznaczenie splotu rozkładów Xj nastręcza wiele trudno-

ści i w praktyce operacji tych dokonuje się w wyjątkowych przypadkach.

Jeśli pomiary poszczególnych wielkości są liczne n > 30 , to rozkłady śred-

nich Xj są zbieżne do rozkładu normalnego.

Zgodnie z centralnym twierdzeniem granicznym splotem rozkładów normal­nych jest rozkład normalny, nawet jeżeli liczba wielkości X j jest ograniczona

np. występują dwie wielkości X, i X₂. Można w tym przypadku przypisać

wartościom współczynnika rozszerzenia wartości zmiennej standaryzowanej Z z tablic rozkładu normalnego dla założonego poziomu ufności (prawdopodobieństwa) .

Dla prób mało licznych n< 30 przyjmuje się, że najlepszym przybliżeniem

rozkładu średniej Xj jest rozkład Studenta. Splot rozkładów Studenta nie jest

rozkładem Studenta. Można jednak rozkład ten przybliżyć rozkładem Studenta wyznaczając efektywną liczbę stopni swobody m_e zgodnie z regułą Welcha-Satterwhite'a.

^U

i--4t

£">«*/

(5-27)

96

gdzie: u_Ay - niepewność standardowa dla średniej Y (zależność 5.26), m^. - niepewność standardowa dla średniej Xj.

Jeżeli liczba m_e uzyskana w wyniku obliczeń nie jest liczbą całkowitą, to należy zaokrąglić ją do najbliższej liczby całkowitej, zawsze w dół.

Przykład 5.4

Aby wyznaczyć objętość walca zmierzono jego średnicę mikromierzem i wyso­kość za pomocą suwmiarki. Każdą z tych wielkości mierzono pięciokrotnie. Uzy­skano następujące wyniki pomiaru: d= (10,21; 10,00; 9,81; 10,22; 10,31)mm, h = = (50,3; 50,4; 50,5; 49,8; 49,5)mm. Ocenić granice niepewności wyniku pomia­rów dla p = 0,95 .

Rozwiązanie

Rozrzut otrzymanych wyników nie wskazuje na popełnienie błędu nadmiernego. Średnie wartości pomiaru średnicy i wysokości

- 1A. 50,55 _1A11 d = — > d. ,= - = 10,1 Imm

M '•» ^

250,0

50,0mm

Zestawienie wyników obliczeń

n	<</	(di-d)	fc-tf	h,	(*,-*)	b-if
	mm	mm	mm^2	mm	mm	mm^2
1	10,21	0,10	0,0100	50,3	0,3	0,09
2	10,00	-0,11	0,0121	50,4	0,4	0,16
3	9,81	-0,30	0,0900	50,0	0,0	0,00
4	10,22	0,11	0,0121	49,8	-0,2	0,04
5	10,31	0,20	0,400	49,5	-0,5	0,25
E	50,55	0	0,1642	250,0	0	0,54

Odchylenie standardowe średniej wartości średnicy

97

Odchylenie średnie kwadratowe dla średniej wysokości

= 0,16mm

Wyznaczenie niepewności standardowych typu B. Założono równomierny roz­kład błędów dla mikromierza i suwmiarki.

_ ^A_g</ _ 0,01

U OJ •" —«." *~ >-_~ '

M_BA=-- = -J*> V3

Wartości te są mniejsze od odpowiednich wartości niepewności typu A i zostają pominięte w obliczeniach. Można zatem przyjąć, że dominującymi są niepewno­ści typu A.

Niepewność standardowa łączna

Objętość walca oblicza się ze wzoru

"4¹ Zatem niepewność łączną

98

= . --10,11-50,0 -0,09²+ --10,1 r -0,16² =

V 2 4

= V5107,0+ 164,8 = 72,6mm³

Ze względu na to, że liczba pomiarów jest niewielka n < 30, współczynnik rozszerzenia należy wyznaczyć dla rozkładu f-Studenta, dla p = 0,95 i efektyw­nej liczby stopni swobody.

Liczbę efektywnych stopni swobody oblicza się ze wzoru

ut 27,8-10*

=5

d/Y 4 (# Y 4

vr K</ ⁺i "M,

od j l d/i J

- (26,05 -10⁶)

Z tablic rozkładu t-Studenta dla m_e = 5 i p = 0,95 współczynnik f ^ = 2,57 . Niepewność rozszerzona

U=k_p-u„= 2,57 • 72,6 = 186,58 »190mm³

Objętość walca

l ₂ l _{2 3}

-- _-.,._ , mm

Wynik pomiaru

V=4010mm³±190mm³

5.4.2. Ocena niepewności typu B

W pomiarach pośrednich, przy ocenie niepewności należy uwzględnić więcej niż jedną niepewność standardową. Niepewności typu A są pomijalnie małe. Po­dobnie jak w punkcie 5.4.1 wartość mierzonej wielkości Y, oraz odchylenie stan­dardowe tej wielkości wyznacza się z zależności

99

Y=f(x,) oraz «^= l£ JL u²_Bi (5.28)

V J'¹ \ ' J

Niepewność rozszerzoną oblicza się z zależności

Aby w tych przypadkach określić wartość współczynnika rozszerzenia, dla danego poziomu ufności należy znać splot rozkładów wielkości pośrednich X_}.

Niepewności typu B wynikające z błędów aparatury pomiarowej, przyjmuje się, że mają rozkład jednostajny. Można przyjąć, że splot trzech lub większej liczby rozkładów jednostajnych staje się zbieżny do rozkładu normalnego. Współczyn­nik rozszerzenia dla założonego poziomu ufności określa się z tablic rozkładu normalnego.

Jeżeli w układzie pomiarowym będą występować dwie składowe niepewno­ści typu B, m_bi i u_B2, wtedy łączna niepewność standardowa przy założeniu, że

| -^7- [ = 1, będzie określona zależnością

;,+«& (⁵-²⁹)

Rozkłady niepewności u_Bl i u_B2, są rozkładami jednostajnymi, splot tych rozkładów jest rozkładem trapezowym. Gdy błędy graniczne a_s, i A_g2 przyrzą­dów pomiarowych są sobie równe, to splot rozkładów jednostajnych jest rozkła­dem trójkątnym. Współczynnik rozszerzenia dla rozkładu trójkątnego, dla danego poziomu ufności określa zależność

k_p=j6-p

Dla innych sytuacji można przyjąć współczynnik rozszerzenia równy 2 dla po­ziomu ufności p = 0,95 lub 3 dla p = 0,99 .

Przykład 5.5

Metodą techniczną woltomierza i amperomierza wyznaczono rezystancję. Napię­cie na oporniku zmierzono woltomierzem magnetoelektrycznym klasy 0,5 o na­pięciu znamionowym U_n =10V, natomiast do pomiaru natężenia prądu użyto

amperomierza magnetoelektrycznego klasy 0,5 o prądzie znamionowym /„ = 1A.

100

W wyniku przeprowadzonego pomiaru otrzymano U _s = 8,2 IV i I_x= 0,501A. Po uwzględnieniu prądu płynącego przez woltomierz otrzymano prąd płynący przez opornik l_x = 0,500A. Należy ocenić niepewność wyniku dla poziomu ufności p = 0,95.

Rozwiązanie

Przyjęto jednostajny rozkład błędów przyrządów pomiarowych. Niepewność typu B pomiaru napięcia i natężenia prądu

A_gv 0,01-0,5-10

A_gA 0,01-0,5-1,0

Niepewność łączną wyraża się wzorem

_{u =}__.(o₎028)²+- -0,0028² =

^{TB V> ;}

0-500 0,500²

= V3,l 36 -10"³+ 8,455 -10'³ = 0,1 07Q

Dla obliczenia niepewności rozszerzonej przyjmuję dla p - 0,95 przyjęto współ­czynnik k_p=2.

Niepewność rozszerzona

^Up=^kp-^uTB=²- °.¹⁰⁷ = 0,214Q = 0,3Q . Wartość mierzonej rezystancji

U 871

r = ±l = _^£1 _{= 16} 42 " I 0,500

Wynik pomiaru

R_x =16,4Q±0,3Q.

101

Przykład 5.6

Moc czynna prądu trójfazowego zmierzono w układzie dwóch watomierzy kl. 0,5; o U„ =100V i /„ =5A, P„ =500W. Po uwzględnieniu poprawek na moc pobraną przez obwody pomiarowe przyrządów, otrzymano następujące wartości: P_wt =320W i P_W2 =410W. Ocenić niepewność pomiaru na poziomie ufności p = 0,95

Rozwiązanie

Składowe niepewności typu B przy jednostajnym rozkładzie błędów.

A ₌ 0,01.05-500

P = p_m + P_W2 = 320 + 410 = 730W Niepewność łączna

4 = 2,03 W

dP₂

Błędy graniczne watomierzy są sobie równe, zatem rozkład wypadkowy będzie rozkładem trójkątnym. Dla rozkładu trójkątnego współczynnik rozszerzenia przyjmuje wartość

*,=V6 -p = 76-0,95 = 2,327

U=k_p-_Urp= 2,327 • 2,03 = 4,7238 1 » 5 W

Niepewność rozszerzona Wynik pomiaru

= P±[/=730W±5W

102

5.4.3. Ocena niepewności typu A i B

W pomiarach pośrednich dla każdej pośredniej wielkości mierzonej X . wy­znacza się, według zasad podanych w rozdziałach 5.4.1 i 5.4.2, niepewności ty­pu A i B. Jeżeli niepewności te mają wartości porównywalne, to oblicza się nie­pewność standardowa łączną dla wielkości X j.

Niepewność standardową dla średniej Y oblicza się ze wzoru

,_y ,-,, (5-3D

dXj

Podobnie, jak w przypadkach poprzednich, jeżeli funkcja f\Xj) jest nieli­niowa, uwzględnia się dodatkowe wyrazy szeregu Taylora, a gdy występują za­leżności miedzy wartościami X_j} oblicza się kowariancję. W pomiarach o naj­większej dokładności zagadnienia dotyczące wyznaczania korelacji są bardzo złożone. Trzeba uwzględnić wszystkie wielkości wpływające oraz wszystkie po­prawki podane w świadectwach kalibracji przyrządów pomiarowych. Zagadnie­nia te są dokładniej omówione w publikacji [3].

W pomiarach pośrednich podstawowym problemem jest ocena współczynni­ka k_p. Przy znacznej liczbie wielkości pośrednich o różnych rozkładach prawdo­podobieństwa wyznaczenie splotu tych rozkładów jest bardzo złożone, a niekiedy niecelowe.

Jeżeli będą spełnione warunki centralnego twierdzenia granicznego, to moż­na współczynnikowi rozszerzenia przypisać wartość zmiennej standaryzowanej Z

0 rozkładzie normalnym. Przy próbach mało licznych, o małej liczbie pomia­
rów, a z takimi przypadkami spotykamy się często w praktyce, lepszą oceną
współczynnika k będzie przypisanie mu wartości zmiennej standaryzowanej

rozkładu f-Studenta dla zadanego poziomu ufności i dla efektywnej liczby stopni swobody m_e.

W skrajnych przypadkach dla oceny współczynnika rozszerzenia można sto­sować metodę przybliżoną przyjmując k_p = 2 dla poziomu ufności p = 0,95

1 k_p - 3 dla poziomu ufności p = 0,99.

103

Przykład 5.7

Aby wyznaczyć natężenie prądu płynącego w badanym obwodzie zmierzono spadek napięcia na rezystorze wzorcowym /?„ = 10Q i klasie dokładności 0,02. Pomiar napięcia przeprowadzono pięciokrotnie za pomocą woltomierza cyfrowe­go na zakresie 10V i błędzie określonym przez producenta jako At/ =0,02%t/^ +0,01%£/„. W wyniku pomiaru otrzymano następujące wartości Ui = (8,545; 8,536; 8,542; 8,538; 8,544)V. Należy wyznaczyć przedział niepew­ności wyników pomiaru dla poziomu ufności p = 0,99.

Rozwiązanie

Ponieważ rezystancja wejściowa woltomierza jest większa od l O⁹ Q, to można pominąć prąd płynący przez jego obwód. Rozrzut otrzymanych wyników nie wskazuje na występowanie błędów nadmiernych. Wartość średnia napięcia

U = - Y U, = -42,705 = 8,54IV n£ ' 5

Zestawienie wyników obliczeń

n	ut	(£/,. -U)	((/,.- U J^2- KT^6
		V	V	V^2
1 2 3 4 5	8,545 8,536 8,542 8,538 8,544	0,004 - 0,005 0,001 -0,003 0,003	16 25 1 9 9
"L	42,705	0	60

Niepewność standardowa typu A

5(5-1)

= 1,7-10-³V

Niepewność standardowa typu B, przy założeniu jednostajnego rozkładu błędów

104

_ _ 0.01 • 0.02 • U + 0,01 • 0,01 • U_n

^Bu

-³-³

"^{= =}

'-⁷'¹⁰ ;'•"'.u.ht«v

Ponieważ niepewności u_Au i u_Bu są tego samego rzędu, to niepewność łączna standardowa pomiaru napięcia

«» = V"L + «L = V(¹>⁷' W³ J +1¹-⁶ • 10"³ / =2,3-l(T³V

Standardowa niepewność dla rezystora, przy jednostajnym rozkładzie błędów

0,01-0,02-10

W_B/f = ;= = 1,2-10

Wartość prądu

R„ 10,0 Niepewność łączna dla natężenia prądu

^łBK

= V5,29 • 10'⁸ + 1,05 • 10~⁸ = 2,5 • 10'⁴ A

Dla poziomu ufności 0,99, z tablic rozkładu normalnego, współczynnik k„= 2,576.

Niepewność rozszerzona

U=k_p-u« =2,576-2,5-10"⁴A = 6,44-10"⁴=7-10"⁴A

Ostateczny wynik pomiaru

I = I±U= 0,854 1A ± 0,0007A

105

W rozpatrywanym przykładzie wykonano tylko niewielką liczbę pomiarów. Współczynnik rozszerzenia zostanie wyznaczony z rozkładu f-Studenta.

Efektywną liczbę stopni swobody, przy występowaniu niepewności typu A i B oblicza się ze wzoru

y Y..4 ,v

m. =•

= 5,82

5(10) ^s ' i( io^! J

m =5

.(1.2.10-')¹

^l '

Z tablic rozkładu Studenta dla p = 0,99 i liczby stopni swobody m_e = 5 ,

^=4,03.

Niepewność rozszerzona

(/ = t_mp • u_a- = 4,03 • 2,5 • 10"⁴ « 10 • KT⁴ A

Ostateczny wynik pomiaru

I = I±U= 0,854 1A ± 0.0010A

Uzyskana wartość przedziahi ufności jest w tym przypadku większa niż przy przyjęciu rozkładu normalnego.

5.5. SPOSOBY ZAPISU WYNIKU POMIARU

Wyniki pomiarów wielkości ciągłych są liczbami przybliżonymi. Sposób prezentacji tych wyników powinien umożliwiać ocenę dokładności ich otrzy­mania.

106

Dokładność liczby przybliżonej określa liczba jej cyfr znaczących. Cyfrą znaczącą jest każda cyfra, z wyjątkiem zer na początku liczby dziesiętnej. I tak np.:

liczba 328,01 ma 5 cyfr znaczących,

liczba 0,023 ma 2 cyfry znaczące,

a liczba 2,30 ma 3 cyfry znaczące.

Zera na końcu liczby są cyframi znaczącymi, należy o tym pamiętać przy zapisie np. liczby 5000. Liczbę tę odczytujemy jako liczbę z czterema cyframi znaczą­cymi. Jeżeli chcemy zaznaczyć, że liczba ta ma mniejszą liczbę cyfr znaczących stosujemy zapis z mnożnikiem 10", np.

liczba o zapisie 50 • l O² ma 2 cyfry znaczące,

a liczba o zapisie 5-10³ ma l cyfrę znaczącą.

Liczbę przybliżoną zaokrągla się tak, aby zawierała tyle cyfr znaczących, że tylko cyfra na ostatnim, najmniej znaczącym miejscu jest cyfrą niepewną, a błąd może wynosić nie więcej niż 5 jednostek następnego nieujawnionego miejsca. Zatem, jeśli wartość rezystancji zapisano w postaci 628,l'Q, to według tej re­guły należy wnioskować, że błąd nie przekracza wartości 0,05'Q.

Reguły te należy stosować przy zapisie wyników danych pomiarowych. Należy przy tym pamiętać, że liczbę cyfr znaczących wyniku determinuje naj­mniejsza jednostka pomiarowa, wynikająca najczęściej z rozdzielczości stosowa­nego przyrządu. Nie można np. poprawki miernika zapisać jako k= 0,035 dz, gdy dokładność odczytu wynosi 0,1 dz. Ta dokładność odczytu, stanowi w tym przy­padku najmniejszą jednostkę pomiarową.

Działania na liczbach przybliżonych, na przykład w pomiarach pośrednich, powinny być wykonywane z taką liczbą cyfr znaczących, aby nie zwiększały w sposób istotny błędu wyniku obliczeń. Należy przy tym pamiętać, że nie wolno zwiększać liczby cyfr znaczących przez zmianę jednostek miar czy mnożenie przez liczbę n. Przyjmuje się, że przy mnożeniu, dzieleniu, potęgowaniu itp. obowiązuje zasada zachowania stałej względnej dokładności. Oznacza to, że sto­sunek cyfry na najmniej znaczącym miejscu do liczby przybliżonej powinien być na takim samym poziomie w wyniku obliczeń jaki jest w liczbie mniej dokładnej. Np.:

3,14-2,1=6,594 = 6,6

0,1:2,1=0,04 oraz 0,5:6,594 = 0,07.

Przy dodawaniu i odejmowaniu, ostatnią cyfrę w wyniku obliczeń zostawia się na tym miejscu po przecinku ile ma liczba mniej dokładna. Np.:

3,14+2,1=5,24=5,2

107

Przypadek oceny dokładności na podstawie liczby cyfr znaczących dotyczy zwykle surowych wyników pomiarowych, z reguły końcowy wynik pomiaru przedstawia się za pomocą dwóch liczb przybliżonych. Jedna z tych liczb jest oceną wartości otrzymaną w wyniku pomiaru, a druga jest oceną granic błędu. Zwykle liczby te przed uporządkowaniem zawierają więcej cyfr, niż jest to uza­sadnione osiągniętą dokładnością pomiaru. Dlatego w końcowym zapisie wyniku należy odrzucić te zbędne cyfry. W pierwszej kolejności zaokrągla się liczbę wy­rażającą granice błędu. Liczbę tę zaokrągla się zawsze „w górę" do jednej cyfry znaczącej. Tylko w szczególnie uzasadnionych przypadkach stosuje się zaokrą­glanie do dwóch cyfr znaczących. Jednym z nich jest zasada polecana przez Mię­dzynarodową Unię Fizyki Czystej i Stosowanej, według której liczbę wyrażającą granice błędu należy zaokrąglać do dwóch cyfr znaczących wtedy, gdy błąd za­okrąglenia przekracza 20%.

Np. obliczone wartości błędu wynoszą:

A!=l,06, A₂=0,821, A₃=241, A4=0,0105. Po zaokrągleniu według podanych wyżej reguł, liczby te należy zapisać: A,=l,l, A₂=0,9, A₃=3-10², A4=0,011.

W drugiej kolejności zaokrągla się liczbę wyrażającą wartość mierzonej wielkości, zostawiając ostatnią cyfrę znaczącą na tym miejscu, na którym wystę­puje ostatnia cyfra znacząca w oszacowaniu błędu. Liczbę tę zaokrągla się „w górę" lub „w dół" w zależności od wartości cyfry odrzucanej:

-jeżeli pierwsza z odrzucanych cyfr jest większa od 5, to ostatnią cyfrę w wyniku pomiaru należy zwiększyć o l,(zaokrąglanie - „w górę")

-jeżeli pierwsza z odrzucanych cyfr jest mniejsza od 5, to ostatnią cyfrę w wyniku pozostawia się bez zmian (zaokrąglanie - „w dół"),

- jeżeli zbędna cyfra jest równa 5, a po niej występuje cyfra różna od zera, to zaokrągla się „w górę",

- jeżeli zbędna cyfra jest równa 5, a po niej następuje zero, to zaokrągla się „do parzystej", co oznacza, że ostatnia cyfra po zaokrągleniu musi być cyfrą pa­rzystą.

Poniżej przedstawiono przykładowe zapisy wyniku pomiaru przed zaokrą­gleniem i po uporządkowaniu zapisu według podanych reguł.

1531,15±0,351=1531,2±0,4

36587125,3±590=(365871,253±6)-10²=(365871±6)-10²

0,00453512±46-10^-6=(454±5)-10'⁵

525,415±0,113=525,42±0,12

6

METODY REGRESJI

6.1. WPROWADZENIE

Często celem doświadczeń polegających na pomiarze wielu różnych wartości kilku różnych wielkości jest zbadanie prawdziwości założonej matematycznej formuły opisującej związek zachodzący pomiędzy jedną z tych wielkości i pozo­stałymi mierzonymi wielkościami. Najprostszym, a zarazem najczęstszym przy­padkiem, jest badanie relacji między dwiema wielkościami, przy tym zakłada się, że ta relacja jest prostoliniowa.

Jeśli zakłada się, że dwie wielkości są związane relacją liniową, to szukana jest linia prosta, która jest najlepiej „dopasowana" do wyników pomiarów. Pro­blem ten można rozwiązać metodą graficzną lub analityczną. Ta analityczna me­toda znajdowania linii prostej, która najlepiej uwzględnia wyniki otrzymane z pomiarów nazywa się metodą regresji liniowej lub metodą najmniejszych kwa­dratów.

Rozszerzeniem problemu jest ocena „dopasowania" znalezionej funkcji, w szczególnym przypadku liniowej do danych pomiarowych. Liczbowych danych do tej oceny dostarcza analiza współczynnika korelacji.

6.2. METODA GRAFICZNA

Metoda graficzna jest stosowana do wyznaczania przebiegu charakterystyk prostoliniowych czyli opisanych zależnością (6. l)

y = A + Bx (6.1)

Rozwiązaniem problemu jest wyznaczenie wartości stałych A i B. W tym celu wyniki pomiarów przedstawia się w postaci punktów w układzie współrzęd­nych prostokątnych x,y, a następnie wykreśla się taką prostą, aby przechodziła przez największą liczbę zaznaczonych punktów lub blisko nich. Współczynniki A i B charakterystyki (6.1) wyznacza się ze współrzędnych dwóch punktów leżą-

109

cych na wykreślonej prostej. Na rysunku 6.1 pokazano tę metodę dla 6-ciu punk­tów pomiarowych.

.^XS

X

-*-

Rys.6. l. Metoda graficzna.

Metodę tę można również zastosować do wyznaczania charakterystyk niektó­rych funkcji nieliniowych. Jest to możliwe przez zastosowanie takiego skalowania współrzędnych aby wykreślona w takim układzie charakterystyka była linią prostą. Na przykład dla charakterystyk potęgowych opisanych zależnością (6.2)

y = A-x^B (6.2)

stosuje się linearyzację przez logarytmowanie obu stron zależności (6.2) czyli

log y = B log x + log A (6.3)

Gdy w wykresie zastosujemy skalę podwójnie logarytmiczną ( czyli na obu osiach współrzędnych), to otrzymany wykres zależności (6.2) powinien być linią prostą.

Dla charakterystyk wykładniczych, jak we wzorze (6.4)

y = A-B^x (6.4)

stosuje się linearyzację przez zastosowanie skali półlogarytmicznej, tzn. dla rzęd­nej y - skala logarytmiczna, a dla odciętej x - skala liniowa, jak to wynika z za­leżności (6.5) otrzymanej w wyniku logarytmowania zależności (6.4).

log y = xlog B + log A

(6.5)

110

Metoda graficzna jest metodą mało dokładną. Zaletą j ej łatwość uzyskania in­formacji pomagających zrozumieniu badanych zjawisk.

6.3. METODA NAJMNIEJSZYCH KWADRATÓW

Metoda najmniejszych kwadratów jest metodą najbardziej ogólną, stosowaną do różnego rodzaju krzywych obrazujących zależności między dwiema wielko­ściami. Metoda ta opiera się na twierdzeniu, że jeżeli suma kwadratów różnic między rzędnymi punktów wyznaczonych z pomiarów i rzędnymi odpowiadają­cych im punktów leżących na hipotetycznej krzywej osiąga minimum, (zobacz zależność (6.6)), to taka krzywa jest najlepiej „dopasowana" do otrzymanych wy­ników pomiarowych.

£(>>,.-y,,)²=min (6.6)

1=1 gdzie

yi - wartości uzyskane z pomiarów, yhi - rzędne punktów leżących na hipotetycznej krzywej. Jest to równoznaczne ze sformułowaniem problemu: znaleźć krzywą, dla której prawdopodobieństwo, że wartości pomierzone znajdą się na krzywej jest największe.

6.3.1. Regresja liniowa

Dla liniowej zależności między wielkościami x i y opisanej wzorem (6.1) należy obliczyć wartości stałych A i B spełniających warunek najmniejszych kwa­dratów. Zakłada się przy tym, że w wyniku pomiarów uzyskano N - punktów pomiarowych: (*/, yi),...,(xn„ yn) oraz, że niepewności w pomiarach wielkości x, są znacznie mniejsze niż niepewności w pomiarach wielkości y_{. Dla poszczegól­nych punktów pomiaru oblicza się różnice - Ay„ uzyskując zależności (6.7).

= y ₂ - y_h2 = y i - (^A + ^Bx2 )= y 2 ~ ^A ~ ^Bx2 » (⁶-⁷)

gdzie oznaczenia jak we wzorze (6.6).

111

Suma kwadratów różnic opisanych wzorem (6.7) wyraża się zależnością

= (Ay, )² + (Ay₂ )² + ... 4- (Ay„ )² = f (A, b) (6.8)

w

Poszukiwanie wartości stałych A i B, dla których funkcja w = f (A, b] osiąga minimum jest równoważne z rozwiązaniem układu równań (6.9)

= 0 i = 0 (6.9)

dA dB

Po podstawieniu do (6.9) zależności (6.7) i (6.8) otrzymuje się układ równań (6.10). Równania ta nazywają się równaniami normalnymi.

(6.10)

N N

Z rozwiązań układu równań (6.10) otrzymuje się najlepsze przybliżenie sta­łych A i B otrzymane metodą najmniejszych kwadratów. Rozwiązania te są posta­ci:

N Y N \ f N Y N

2

₍₆.11)

I

ł ^JY -s«

h ^²

M S'? -1.*,

/=!

(6.12)

Linia prosta o stałych obliczonych według zależności (6.11) i (6.12) nazywa się prostą regresji zmiennych y i x.

112

Zakładając, że znana jest niepewność pomiarów y\_iK<y_N i stosując prawo

przenoszenia niepewności do wyrażeń (6.11) i (6.12) opisujących stałe A i B można oszacować niepewności tych stałych. Ich wariancje będą odpowiednio równe:

(6.13)

u²_B = N-u²_y/M

gdzie:

u_a - jest niepewnością stałej A,

m_b -jest niepewnością stałej B,

u_y - niepewność pomiarów y, ,K , y_N ,

M - jest wyrażeniem opisanym zależnością (6. 14).

Współczynnik korelacji liniowej

Słuszność hipotezy liniowej zależności między wielkościami x, y może być oceniana wieloma metodami. Jedna z nich polega na sprawdzeniu, czy punkty pomiarowe leżą dostatecznie blisko linii prostej o obliczonych stałych A i B po­przez wyznaczenie ich niepewności według wzorów (6.13). W metodzie tej ko­nieczna jest znajomość niepewności pomiarów x_t i y_t. W przypadku trudności z oszacowaniem niepewności danych x_h y_t ,stopień, w jakim punkty (je,, y, ),K , (jc^, y_N )potwierdzają hipotezę liniowości , wyraża współczynnik ko­relacji liniowej - r. Współczynnik ten oblicza się według wzoru (6.15).

1=1

113

Wartość liczbowa współczynnika korelacji liniowej - r może mieć wartości od -l do +1. Jeżeli r jest bliskie ±1, to punkty są rozłożone wzdłuż pewnej pro­stej; jeżeli r jest bliskie O, to punkty są nieskorelowane i nie wyznaczają prostej. W przypadkach przybierania przez r wartości pośrednich należy skorzystać z oceny prawdopodobieństwa uzyskania na podstawie N pomiarów nieskorelowa-nych zmiennych x i y współczynnika r większego od określonej wartości r₀. Co można zapisać:

(6.16)

Prawdopodobieństwo to (wyrażone w %), dla różnej liczby pomiarów - N i różnych wartości r₀ podano w tabeli 6. l .

Aby skorzystać z tabeli 6.1 należy najpierw na podstawie punktów pomia­rowych obliczyć współczynnik korelacji - r₀. Następnie z tabeli należy odczy­tać prawdopodobieństwo, że N nieskorelowanych par da współczynnik korelacji nie mniejszy niż obliczony - r₀. Jeżeli prawdopodobieństwo to jest wystarczają­co małe, to można wnioskować, że jest mało prawdopodobne, aby zmienne x i y były ze sobą nieskorelowane, a więc jest bardzo prawdopodobne, że są one sko­relowane.

Tabela 6.1

r.	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8 |0,9 |1,0
N	pn%
3	100	94	87	81	74	67	59	51	41	29	0
6	100	85	70	56	43	31	21	12	6	1	0
10	100	78	58	40	25	14	7	2	0,5	-	0
20	100	67	40	20	8	2	0,5	0,1	-	-	0
50	100	49	16	3	0,4	-	-	-	-	-	0

6.3.2. Regresja wielomianowa

Regresja liniowa jest szczególnym przypadkiem szerokiej klasy zagadnień znajdowania krzywych obrazujących relację między dwiema zmiennymi x i y. Często zakłada się, że zmienna y daje się wyrazić za pomocą wielomianu zmien­nej x:

"+A+£x" (6.17)

Stosując do wielomianu (6.17) metodę najmniejszych kwadratów uzyskuje się układ równań normalnych o postaci

114

N N N N

1=1 (=1 1=1 1=1

N N _N N

n ,

i=l i=l 1=1 1=1

Rozwiązanie tego układu («+/) równań to wyrażenia opisujące najlepsze przybliżenia współczynników A,B,...,K, krzywej opisanej wzorem (6.17), zwanej krzywą regresji wielomianowej.

Należy zauważyć, że im wyższy stopień wielomianu, tym rozwiązywanie układu równań normalnych jest bardziej czasochłonne. Istnieją programy kom­puterowe, które pozwalają zminimalizować tę trudność.

6.3.3. Regresja wielokrotna

Regresja wielokrotna dotyczy zagadnień wzajemnych zależności między więcej niż dwiema zmiennymi. Najprostszy przypadek regresji wielokrotnej doty­czy trzech zmiennych x, y, z, z których jedna - z zależy liniowo od dwóch pozo­stałych, co można opisać zależnością:

z = A + Bx + Cy (6.19)

Przypadek ten można rozwiązać przez uogólnienie metody najmniejszych kwadratów stosowanej przy dwóch zmiennych. Założenia są następujące:

1. wykonano serię pomiarów wielkości x, y, z, uzyskując wyniki x_it y i, z_h
   i=l,...,N

2. wyniki z/ - mają jednakowe niepewności,

3. niepewności wyników x_h i y_t są pomijalnie małe.

Zastosowanie zasady największego prawdopodobieństwa czyli metody naj­mniejszych kwadratów prowadzi do układu równań normalnych opisanych zależ­nościami (6.20)

115

N N

S*, + *|>,² + CJ^y,. = j^_x,y,, (6.20)

/=! i=l 1=1 ;=1

N N N N

Równania te należy rozwiązać względem A, B i C, aby otrzymać najlepsze dopasowanie funkcji (6.19) do otrzymanych wyników pomiaru.

116

LITERATURA

[I] Chwaleba A., Pomiński M., Siedlecki A.: Metrologia elektryczna. WNT,
Warszawa 1996.

[2] Dudziewicz J., praca zbiorowa: Etalony i precyzyjne pomiary wielkości

elektrycznych. PWN, Warszawa 1982. [3] Guide to the Expression of Uncertainty in Measurement. ISO 1993, 1995.

Tłum. poi.: Wyrażanie niepewności pomiaru. Przewodnik. GUM 1999. [4] Jaworski J.M.: Niedokładność pomiaru w procesie nauczania metrologii.

XXXII Międzyuczelniana Konferencja Metrologów, Rzeszów 2000. [5] Jaworski J.M.: Problem niedokładności w wykładzie. Metrologia

elektryczna. XXXII Międzyuczelniana Konferencja Metrologów,

Rzeszów 2000. [6] Jaworski J.M., Morawski R. Z., Olędzki J. S.: Wstęp do metrologii i

techniki eksperymentu. WNT, Warszawa 19992. [7] Jaworski J.: Błąd i niepewność pomiaru bezpośredniego. Pomiary,

Automatyka, Robotyka 9/1999 [8] Jaworski J.: Błąd i niepewność pomiarów pośrednich. Pomiary,

Automatyka, Robotyka 10/1999 [9] Jaworski J.: Błąd i niepewność przyrządów pomiarowych. Pomiary,

Automatyka, Robotyka 11/1999 [10] Jaworski J.: Niedokładność, błąd, niepewność. XXIX MKM, Nałęczów

Tl 1997

[II] Kalus-Jęcek B., No wieki R.: Podstawy miernictwa elektrycznego dla
elektroników. Skrypt Politechniki Łódzkiej, Łódź 1995.

[12] Kuśmierek Z.: Podstawy metrologii elektrycznej. Wzorce i teoria

pomiarów. Skrypt Politechniki Łódzkiej, Łódź 1990. [13] Kuśmierek Z., praca zbiorowa: Metrologia elektryczna i elektroniczna.

Ćwiczenia laboratoryjne. Skrypt Politechniki Łódzkiej, Łódź 2000. [14] Lisowski M.: Prawo o miarach w świetle przepisów i norm. Normalizacja

1/1996,8.15-18. [15] Sochocka D., Stanioch W.: Odtwarzanie i przekazywanie jednostki

napięcia elektrycznego w Głównym Urzędzie Miar. XXXII

Międzyuczelniana Konferencja Metrologów, Rzeszów 2000. [16] Taylor J. R.: Wstęp do analizy błędu pomiarowego. PWN, Warszawa

1995. [17] Turzeniecka D.: Ocena niepewności wyniku pomiaru. Wyd. Politechniki

Poznańskiej, Poznań 1997.

117

NORMY

[18] PN-90/E-06508. Oporniki dekadowe. Ogólne wymagania i badania. [19] PN-90/E-06509. Oporniki wzorcowe. Ogólne wymagania i badania. [20] PN-80/E-06531. Ogniwa wzorcowe. Wymagania ogólne. [21] PN-88/E-01100. Oznaczenia wielkości i jednostek miar używanych w elektryce. Postanowienia ogólne. Wiadomości podstawowe..

---