Wydział: FTiMK	Imie i Nazwisko: Marcin Wiśniowski	Nr. Zepołu 8	Ocena Ostateczna
Grupa: Trzecia	Tytół ćwiczenia: Siatka Dyfrakcyjna	Nr. Cwiczenia 28	Data Wykonania: 19.10.2001

1. Wprowadzenie

Siatka dyfrakcyjna to układ N wzajemnie równoległych i rozmieszczo­nych w równych odstępach szczelin. Odległość d środków sąsiednich szcze­lin nazywamy stałą siatki. Dyfrakcja światła na układzie N szczelin jest roz­szerzeniem interferencyjno-dyfrakcyjnego eksperymentu z dwoma szczeli­nami. Jeżeli na siatkę pada równoległa wiązka światła monochromatycznego o długości A, to każda szczelina będzie źródłem pęku promieni ugiętych pod różnymi kątami. Otrzymany rozkład natężenia światła na ekranie jest podobny do obrazu otrzymanego w przypadku dwóch szczelin i składa się z serii prążków interferencyjnych, których względne natężenie modulowane jest przez obraz dyfrakcyjny pojedynczej szczeliny.

Promienie, wychodzące ze wszystkich szczelin i tworzące z pierwotnym kierunkiem kąt a, będą się wzajemnie wzmacniały, gdy różnica dróg δ mię­dzy dwoma sąsiednimi ugiętymi promieniami równa jest wielokrotności długości fali.

δ = dsinα_n = nλ, n = 0, 1, 2, 3,...

Równanie to określa położenie maksimów głównych natężenia światła. Oznacza to, że odległość kątowa prążków jest określona stosunkiem X/d i nie zależy od liczby szczelin N.

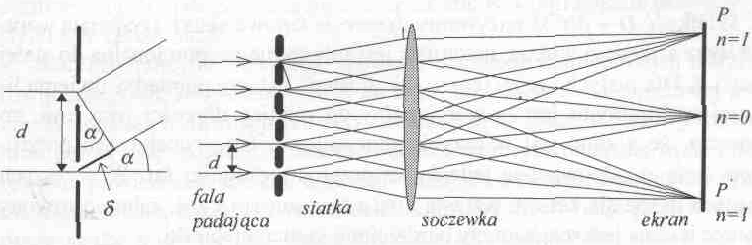
Jeżeli padające światło jest mieszaniną fal o różnych długościach, to położenia maksimów natężenia odpowiadają różnym kątom a_n. Każdy rząd rozciąga się w widmo pierwszego, drugiego, n-tego rzędu. Liczba otrzymywanych rzędów jest ograniczona stałą siatki d, zgodnie z warunkiem:

Ze wzrostem liczby szczelin N maleje szerokość maksimów głównych, pomiędzy nimi pojawia się N-1 minimów bocznych oraz N-2 maksimów wtórnych o bardzo małym natężeniu, wywołanych wzmacnia­niem się promieni pochodzących z mniejszej liczby szczelin. Położenie ką­towe k-tego minimum, leżącego pomiędzy kolejnymi maksimami głównymi określa równanie:

n = 0, 1, 2, ..., N-1

2. Metoda pomiaru

W celu wyznaczenia długości fali światła emitowanego przez źródło ze­stawiamy przyrządy: lampa rtęciaowa, szczelina w kolimatorze, siatka, soczewki i ekran. Badane światło pada na szcze­linę S o regulowanej szerokości, umieszczona w ognisku kolimatora (kolimator jest to rura metalowa wewnątrz poczerniona, zaopatrzona z jednej strony w soczewkę skupiającą, w ognisku której znajduje się zasłona ze szczeliną). Dzięki temu wiązka światła padająca na siatkę jest wiązka pro­mieni równoległych. Światło po ugięciu na siatce dyfrakcyjnej pada na so­czewkę skupiająca, umieszczona za siatką, która ogniskuje promienie na ekranie, dając rzeczywiste obrazy szczeliny, ugięte pod różnymi kątami. Za­stosowany układ soczewek skupiających zapewnia warunki dyfrakcji Fraun-hofera.

	n = 1
		n = 0
		n = 1

Za pomocą tego układu można wyznaczyć sinus konta ugięcia dowolnego maximum interferencyjnego:

wtedy po podzstawieniu:

3. Tabele pomiarowe i obliczenia.

L = 43,1 cm = 0,431 m ΔL = (0,003 m + 0,006 m + 0,001 m)/2 = 0,005m
Rząd widma n	Barwa światła	2yn mm	yn ± Δyn mm	λ mm
I	Fioletowa	74	37 ± 0,5	427,66
		Zielona	92	46 ± 0,5	530,62
		Pomarańczowa	98	49 ± 0,5	564,80
	II	Fioletowa	148	74 ± 0,5	427,66
		Zielona	188	94 ± 0,5	553,42
		Pomarańczowa	200	100 ± 0,5	587,54

• Obliczanie wartości atałej siatki d oraz niepewności maksymalnej Δd.

d ⋅ k = d_ok ⋅ n → d_ok ⋅ 11 = d ⋅ 1,5

d_w ⋅ k' = d_ok ⋅ n' → d_w ⋅ 5,5 = d_ok ⋅ 1,5

= d_w ⋅ 5,5 ⋅ 1,5 / 1,5 ⋅ 11 = 0,0050 [mm] = 0,5 ⋅ 10^-5 [m]

Δy_n = 0,5 [mm]

d = (0,50 ± 0,4) ⋅ 10^-5 [m]

• Obliczanie długości fali każdej z linii :

Dla barwy fioletowej i n=1:

Pozostałe obliczenia wykonano w analogiczny sposób. Korzystając z otrzymanych wartości liczymy długości fal dla każdej barwy jako średnią.

λ_f - długość fali dla barwy „fioletowej”

λ_z - długość fali dla barwy „zielonej”

λ_p - długość fali dla barwy „pomarańczowej”

λ_f = (427,66 nm + 427,66 nm)/2 = 427,66 nm

λ_z = (530,62 nm + 553,42nm)/2 = 542,02 nm

λ_p = (564,80nm + 587,54nm)/2 = 576,17 nm

• Obliczanie niepewności maksymalnej Δλ metodą rózniczki zupełnej dla pomiaru barwy fioletowej przy n=1

Ostatecznie dłógość fali λ barwy fioletowej wynosi:

λ = (427,66 ± 348,11) [nm]

4. Wnioski:

Długość fali barwy fioletowej wyliczona:

427,66 ± 348,11 [nm]

Długość fali barwy fioletowej tablicowa:

397 - 424 [nm]

Wartość długości fali wyliczona jest zbliżona do tablicowej.

Niepewność pomiaru długości fali λ wynikła przede wszystkim z małej dokładności określenia stałej siatki dyfrakcyjnej d. Prawdopodobnie zwiększenie ilości pomiarów wielkości d, y_n niepewności uległy by zmieszeniu, gdyż umożliwiało by to wykluczenie błędów pomiarowych grubych. Wracając do porównania wyników otrzymanych z tablicowymi dla pozostałych barw. Wnioskuje że ich zbliżoność jest nie przypadkowa i świadczy o staranie wykonanym ćwiczeniu

---