LABORATORIUM FIZYKI I |
Ćwiczenie nr 28 |
||
Wydział Mechatronika |
Grupa 22 |
Zespół 9 |
Data 4 - I - 1999 |
Nazwisko i imię: Andrzej Skalski
|
Przygotowanie |
||
Temat ćwiczenia: Badanie zjawiska skręcenia płaszczyzny polaryzacji światła |
Zaliczenie |
||
Podstawy teoretyczne
Światło w zjawisku interferencji, dyfrakcji oraz polaryzacji zachowuje się jak fala elektromagnetyczna, a więc rozchodzi się w przestrzeni w ciąg zmiennych pól elektrycznych i magnetycznych wzajemnie się wytwarzających. Światło może być spolaryzowane liniowo, kołowo lub eliptycznie. Polaryzacja liniowa jest wówczas, gdy drgający wektor pola elektrycznego oraz wektor falowy wyznaczają nie zmieniającą się w przestrzeni płaszczyznę. Gdy koniec wektora natężenia pola elektrycznego fali opisuje linia śrubowa, kołowa bądź eliptyczna to mówimy wówczas o polaryzacji liniowej lub eliptycznej.
Ćwiczenie polegało na pomiarze kąta skręcenia płaszczyzny polaryzacji fali świetlnej. W tym celu użyliśmy układu polaryzatorów.
Materiały optyczne czynne dzielimy na dwie grupy:
aktywne optyczna wywołana polem magnetycznym
naturalna aktywność optyczna
W ćwiczeniu badaliśmy oba rodzaje materiałów optycznie czynnych.
Pomiary, obliczenia i wykresy
Naturalna aktywność optyczna.
α - kąt skręcenia płaszczyzny drgań
h - grubość warstwy roztworu h = 155±2 mm
c - stężenie roztworu
Jako materiał optycznie czynny użyliśmy roztworu cukru w wodzie.
Wyniki pomiarów kąta skręcenia płaszczyzny polaryzacji w zależności od stężenia roztworu cukru w wodzie c.
c [%] |
0 |
2 |
4 |
7,4 |
10 |
13,8 |
17 |
? |
α1 |
35,7o |
37,02o |
38,9o |
42,4o |
46,1o |
50,4o |
52,75o |
42,65o |
α2 |
35,7o |
37,0o |
38,8o |
42,6o |
46,2o |
50,25o |
52,7o |
42,9o |
α3 |
35,6o |
37,05o |
39,0o |
42,6o |
46,2o |
50,25o |
52,9o |
43,05o |
α4 |
35,35o |
37,0o |
39,05o |
42,6o |
46,15o |
50,35o |
53,0o |
42,95o |
αśr |
35,6o |
37,02o |
38,94o |
42,56o |
46,16o |
50,31o |
52,84o |
42,89o |
αw |
0o |
1,42 o |
3,34 o |
6,96 o |
10,56 o |
14,71 o |
17,24 o |
7,29o |
Δαw |
0,08 o |
0,01 o |
0,06 o |
0,05 o |
0,02 o |
0,04 o |
0,07 o |
0,09 o |
Wykres zależności kąta skręcenia płaszczyzny polaryzacji w zależności od stężenia roztworu :
Z wykresu wynika, że a = 1,06±0,03 możemy więc wyliczyć właściwe skręcenie γ:
Podstawiając wartości do wzorów otrzymujemy
γ=0,0068±0,0003 [10/mm]
Odczytując z wykresu wartość nieznanego stężenia roztworu otrzymujemy:
c = 8,9±0,3 %
Natomiast obliczając tę wartość mając znane γ otrzymujemy:
Podstawiając wartości do wzoru otrzymujemy:
c = 6,9±0,2 %
Aktywność optyczna wywołana polem magnetycznym
Do badania wpływu pola magnetycznego na wartość kąta skręcenia płaszczyzny polaryzacji użyliśmy szkła SFS1 (ciężki filtr), który został umieszczony w cewce o parametrach:
N = 4200 -liczba zwojów
L = 280±1 mm -długość solenoidu
h = 86,0±0,5 mm -długość pręta szklanego
Wyniki przeprowadzonych pomiarów:
I [A] |
0 |
0,6 |
1,21 |
1,8 |
2,4 |
3 |
3,6 |
4,2 |
4,8 |
α1 [0] |
71,5 |
72,7 |
74,7 |
76,2 |
77,5 |
79,55 |
81 |
82,5 |
83,9 |
α2 [0] |
71,6 |
73 |
74,8 |
76,15 |
77,65 |
79,4 |
80,95 |
82,35 |
83,85 |
α3 [0] |
71,6 |
73,2 |
74,85 |
76,3 |
77,85 |
79,4 |
80,95 |
82,4 |
83,75 |
α4 [0] |
71,8 |
73,1 |
74,8 |
76,2 |
77,7 |
79,25 |
81 |
82,45 |
83,9 |
αśr [0] |
71,63 |
73,0 |
74,79 |
76,21 |
77,68 |
79,40 |
80,98 |
82,43 |
83,85 |
αw [rad] |
0 |
0,024 |
0,0552 |
0,0801 |
0,1056 |
0,136 |
0,1632 |
0,1885 |
0,2134 |
Δαw [rad] |
0,001 |
0,002 |
0,0005 |
0,0005 |
0,0013 |
0,001 |
0,0003 |
0,0006 |
0,0006 |
B [t] |
0 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
Wykres zależności kąta skręcenia płaszczyzny polaryzacji od prądu w cewce:
Korzystając z metody najmniejszych kwadratów wyliczamy stałą Verdeta przyjmując:
x = B, y=α, otrzymujemy a = V*h = 2,698±0,025 stąd
Podstawiając wartości do powyższych wzorów otrzymujemy:
V = 1,72±0,03 [10/mm] = 31,4±0,5 [rad/m]
Mając daną stałą Verdeta możemy obliczyć wartość e/m z wzoru:
Gdzie λ=589,3 nm, c -prędkość światła, dλ=λ1-λ2=45,5 nm, dn = n1-n2 = 0,00873
Podstawiając powyższe wartości do wzoru na e/m otrzymujemy:
Wnioski
Zauważamy dość duże rozbieżności w obliczonych stężeniach roztworu dla pierwszej części ćwiczenia. Biorąc pod uwagę tabelę przedstawiającą zależność kąta odchylenia płaszczyzny polaryzacji światła przechodzącego przez roztwór cukru w wodzie, możemy spodziewać się, że wartość szukanego stężenia roztworu będzie znajdować się w zakresie wartości 7,4-10. Temu zakresowi odpowiada wartość stężenia odczytana z wykresu. Stężenie wyliczone z wzoru, przy założeniu, że znamy właściwe skręcenie płaszczyzny polaryzacji " " znajduje się poza oczekiwanym przedziałem. Wynika stąd, że albo błędnie została wyliczona wartość właściwego skręcenia płaszczyzny polaryzacji, albo błędna jest zależność z której liczyliśmy stężenie.
Stała Verdeta wyliczona z drugiej części ćwiczenia różni się o 10% od wartości teoretycznej Vt=33.13[rad/m]. Ponieważ błąd wartości wyznaczonej doświadczalnie jest dużo mniejszy niż 10% musimy stwierdzić że obliczona przez nas doświadczalna wartość stałej Verdeta nie może być uznana za poprawną.
Zastosowane przez nas metody obliczeniowe są zbyt niedokładne aby można było za ich pomocą liczyć wartości skręcenia właściwego, bądź stałej Verdeta. Można natomiast stwierdzić przydatność tych metod do obserwowania zależności kąta skręcenia płaszczyzny od stężenia roztworu lub indukcji magnetycznej.
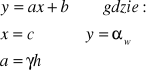
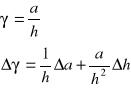
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 10, Sprawozdanie z laboratorium z fizyki i biofizyki
Ćwiczenie (28), cw28 sprawko
Wyznaczanie naprężeń za pomocą tensometru oporowego, Laboratorium z fizyki - cwiczenia
01, Cwiczenie 01 g, Laboratorium z fizyki
sprawozdanie z laboratorium fizyki nr 28!, Raport elegancki
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 2, Sprawozdanie z laboratorium z fizyki i biofizyki
InstrukcjeĆw.2009 2010, Cw.1.E-01. Badanie właściwości elektrycznych kondensatora płaskiego, Laborat
4SPRAWOZDANIE DO CWICZENIA LABORATORYJNEGO Z FIZYKI BUDOWLI
Fiza - MK1, Laboratorium z fizyki - cwiczenia
FIZYKA-sprawozdania, 22a, ĆWICZENIA LABORATORYJNE Z FIZYKI
cwiczenia laboratoryjne z fizyki
InstrukcjeĆw.2009 2010, Cw.3.M-01,M-02.Równia pochyła.Wahadło, Laboratorium Fizyki; ćwiczenie Nr 1
Wyznaczanie momentu bezwladnosci, Cwiczenie 01 g, Laboratorium z fizyki
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 9, Sprawozdanie z laboratorium z fizyki i biofizyki
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 7, Sprawozdanie z laboratorium z fizyki i biofizyki
więcej podobnych podstron