Sprawozdanie z laboratorium z fizyki i biofizyki
Ćwiczenie nr 2
Temat ćwiczenia: Wyznaczanie momentów bezwładności brył sztywnych metodą zawieszenia trójnitkowego.
Data wykonania ćwiczenia: 22. 04. 2008 r.
Sekcja nr 8 w składzie:
1. Andrzej Michalski
2. Robert Jała
3. Piotr Apczyński
Data oddania sprawozdania:
Ocena:
Wstęp teoretyczny:
Bryła doskonale sztywna jest bryłą, której elementy nie mogą się względem siebie przemieszczać. Wszystkie punkty mają jednakowe prędkości i przyspieszenia.
Ruch postępowy charakteryzuje się tym, że wszystkie punkty ciała przemieszczają się z prędkościami o jednakowych kierunkach, zwrotach i wartościach.
Ruch obrotowy to taki ruch, w którym wszystkie punkty bryły sztywnej poruszają się po okręgach o środkach leżących na jednej prostej zwanej osią obrotu. Oś ta jest prostopadła do płaszczyzny tych okręgów.
Moment bezwładności jest to miara bezwładności ciała w ruchu obrotowym względem określonej, ustalonej osi obrotu. Zależy on od masy ciała i jej rozkładu względem osi obrotu.
Moment bezwładności bryły określany jest wzorem:
gdzie:
m - masa punktów ciała oddalonych od osi obrotu o długość r;
r - odległość tych punktów od osi obrotu.
Dla ciał rozciągłych wynosi on:
gdzie
dm - nieskończenie małe elementy ciała
r - odległość każdego takiego elementu od osi obrotu.
Przebieg ćwiczenia:
Bryłę, której moment bezwładności będziemy wyznaczać, położyliśmy na poziomej, jednorodnej tarczy kołowej, zawieszonej na 3 niciach o jednakowych długościach. Nici są ulokowane w jednakowych odległościach od środka tarczy, tak, aby tworzyły wierzchołki trójkąta równobocznego.
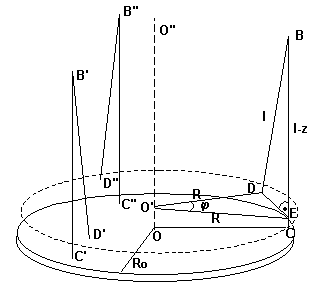
Na początku zmierzyliśmy promień i masę tarczy kołowej i obliczyliśmy jej moment bezwładności.
W dalszej kolejności kładliśmy poszczególne bryły na tarczy. Obracaliśmy ją o promień 5 st. i notowaliśmy czas 10 wahnięć. Pomiary dla każdej z 5 brył powtarzaliśmy sześciokrotnie. Na tej podstawie obliczyliśmy okres drgań tarczy. Następnie wyznaczyliśmy momenty bezwładności każdej z brył wykorzystując do tego obliczony przez nas okres drgań T oraz wyliczoną stałą C. W końcowym etapie obliczyliśmy momenty bezwładności poszczególnych brył, z wykorzystaniem ich wymiarów po podstawieniu do znanych wzorów. Dla walca o promieniu r. wzór ten ma postać: ![]()
. Natomiast dla prostopadłościanu wynosi on: ![]()
,
gdzie W i L są krawędziami bryły.
Tabele wyników:
Typ ciała |
Czas [s] dla 10 wahnięć |
Średni czas |
Okres T [s] |
|||||
Drewniany prostopadłościan 140g |
10,65 |
11,30 |
10,47 |
10,25 |
10,51 |
10,39 |
10,60 |
1,06 |
Metalowy walec |
10,29 |
10,61 |
10,46 |
10,20 |
10,39 |
10,42 |
10,40 |
1,04 |
Cienki metalowy krążek |
9,73 |
9,62 |
9,47 |
9,52 |
9,49 |
9,68 |
9,58 |
0,96 |
Gruby metalowy krążek |
8,06 |
8,10 |
8,19 |
8,22 |
8,12 |
8,08 |
8,13 |
0,81 |
Drewniany prostopadłościan 120g |
11,09 |
11,88 |
11,10 |
11,28 |
11,43 |
11,14 |
11,32 |
1,13 |
Typ ciała |
Masa |
Wymiary [cm] |
Drewniany prostopadłościan 140g |
140 g |
8 x 8 x 4,5 |
Metalowy walec |
110 g |
R=1,9 L=3,4 |
Cienki metalowy krążek |
200 g |
R=3,9 L=1,5 |
Gruby metalowy krążek |
400 g |
R=4 L=2,9 |
Drewniany prostopadłościan 120g |
120 g |
11 x 11 x 1,9 |
Tarcza:
r = 12,5 cm
m = 180 g
Długość nici: L = 85 cm
Wyniki:
Moment bezwładności tarczy:
![]()
I0 = ![]()
= 0,0014 [kg * m2] ![]()
Na postawie poniższego wzoru na okres drgań tarczy, wyprowadzamy wzór na moment bezwładności
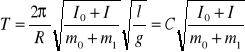
I = ![]()
gdzie 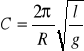
Obliczamy stałą C:
C= 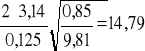
![]()
Momenty bezwładności dla poszczególnych brył
a) Drewniany prostopadłościan 140g
I = 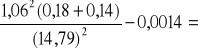
0,00024 ![]()
b) metalowy walec
I = 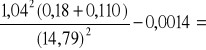
0,0003 ![]()
c) cienki metalowy krążek
I = 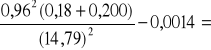
0,0002 ![]()
d)gruby metalowy krążek
I = 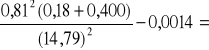
0,00034 ![]()
e) drewniany prostopadłościan 120g
I = 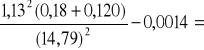
0,00035 ![]()
Momenty bezwładności dla poszczególnych brył z wykorzystaniem ich wymiarów:
a) Drewniany prostopadłościan 140g; m=0,140 kg; L=0,08m; W=0,08m
![]()
![]()
0,00015 ![]()
b) metalowy walec; m=0,11 kg; r=0,019m
![]()
![]()
0,0002 ![]()
c) cienki metalowy krążek; m=0,2 kg; r=0,039m
![]()
![]()
0,00015 ![]()
d) gruby metalowy krążek; m=0,4 kg; r=0,04m
![]()
![]()
0,00032 ![]()
e) drewniany prostopadłościan 120g; m=0,120 kg; L=0,11m; W=0,11m
![]()
![]()
0,00024 ![]()
Analiza błędów
dT = 0,01s
dm0 = 0,001g
dm1 = 0,001g
dC = 0,001m
a) Drewniany prostopadłościan 140g; m1=0,140 kg; T=1,06; m0=0,18 kg; C=14,79
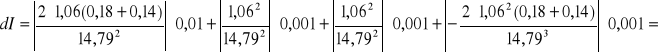
0,00004 ![]()
b) metalowy walec; m1=0,11 kg; T=1,04; ; m0=0,18 kg; C=14,79
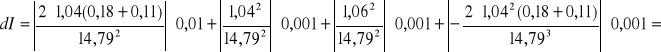
0,00004 ![]()
c) cienki metalowy krążek; m=0,2 kg; T=0,96; m0=0,18 kg; C=14,79
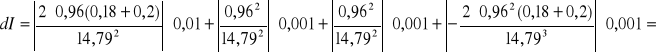
0,00004 ![]()
d) gruby metalowy krążek; m=0,4 kg; T=0,81; m0=0,18 kg; C=14,79
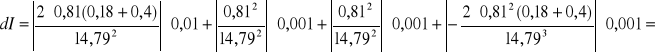
0,00005 ![]()
e) drewniany prostopadłościan 120g; m=0,120 kg; T=1,13; m0=0,18 kg; C=14,79
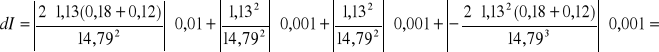
0,00004 ![]()
Wyniki końcowe:
a) Drewniany prostopadłościan 140g
I = 0,00024 ![]()
0,00004 ![]()
b) metalowy walec
I = 0,0003 ![]()
0,00004 ![]()
c) cienki metalowy krążek
I = 0,0002 ![]()
0,00004 ![]()
d) gruby metalowy krążek
I = 0,00034 ![]()
0,00005 ![]()
e) drewniany prostopadłościan 120g
I = 0,00035 ![]()
0,00004 ![]()
Wnioski:
Wyniki momentów bezwładności jakie uzyskaliśmy z wykorzystaniem mierzonego T, w niewielkim stopniu odbiegają od wartości obliczonych na podstawie masy i wymiarów brył.
Mogło to być spowodowane niedokładnym wykonaniem pomiarów brył i tarczy, a także zawodnością ludzkiego oka podczas ustalania kąta według którego obracaliśmy tarczę wraz z bryłą.
Przyczyną powstałych błędów pomiarowych mogły być również niezbyt precyzyjne pomiary okresu drgań.
Wyszukiwarka
Podobne podstrony:
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 9, Sprawozdanie z laboratorium z fizyki i biofizyki
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 7, Sprawozdanie z laboratorium z fizyki i biofizyki
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 10, Sprawozdanie z laboratorium z fizyki i biofizyki
Sprawozdanie z laboratorium z fizyki i biofizyki04, fiza lab
Sprawozdanie z laboratorium z fizyki
PRAWO?RNULLIEGO Sprawozdanie z laboratorium z fizyki
SPRAWOZDANIE Z LABOLATORIUM Z FIZYKI I BIOFIZYKI cw.5, biotechnologia inż, sem2, FiB, laborki, spraw
sprawozdanie z laboratorium fizyki nr 28!, Raport elegancki
Sprawozdanie z laboratorium z fizyki
bernuli-Notatek.pl, Sprawozdanie z laboratorium z fizyki
sprawozdanie z laboratorium fizyki nr 37, Raport elegancki
3.1 b, Politechnika Lubelska, Studia, Studia, materiały na studia, Laboratorium fizyki, sprawozdani
sprawozdanie z laboratorium fizyki nr 1, sprawka fizyka
EM 3.2, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, L
SPRAWOZDANIE Z LABOLATORIUM Z FIZYKI I BIOFIZYKI cw.6, sprawka
W2 - SprawozdanieM, Laboratorium fizyki CMF PŁ
więcej podobnych podstron