Sprawozdanie z laboratorium z fizyki i biofizyki

Ćwiczenie nr 10

Temat ćwiczenia: Badanie siły elektromotorycznej Faraday'a

Data wykonania ćwiczenia: 8. 04. 2008 r.

Sekcja nr 8 w składzie:

1. Andrzej Michalski

2. Robert Jała

3. Piotr Apczyński

Data oddania sprawozdania:

Ocena:

I Wstęp teoretyczny:

Indukcja elektromagnetyczna - zjawisko powstawania siły elektromotorycznej w przewodniku pod wpływem zmiennego pola magnetycznego lub ruchu przewodnika w polu magnetycznym, odkryte w 1831 roku przez angielskiego fizyka Michaela Faradaya.

Prąd indukcyjny - prąd elektryczny płynący w zamkniętym obwodzie elektrycznym lub w substancji przewodzącej prąd elektryczny wywołany indukcją elektromagnetyczną np. z powodu umieszczenia obwodu w zmiennym polu magnetycznym.

Prąd indukcyjny można uzyskać różnymi sposobami. Jedynym z nich jest otrzymywanie prądu indukcyjnego przez zbliżanie i oddalanie od zwojnicy innej zwojnicy przez która płynie prąd. Zmienne pole magnetyczne można także uzyskać włączając i wyłączając prąd w obwodzie pierwotnym, zmieniając jego natężenie lub obwód pierwotny zasilić prądem zmiennym.

Ferromagnetyk to substancja o bardzo silnych własnościach magnetycznych. Własności te biorą się stąd, że każdy atom ferromagnetyka wytwarza własne pole magnetyczne. Co więcej atomy te mają tendencję do ustawiania się w ten sposób, aby ich pole magnetyczne miało ten sam kierunek, co pole magnetyczne atomów sąsiednich. W rezultacie tworzą się duże obszary (w porównaniu z rozmiarami pojedynczego atomu), w których pole magnetyczne ma stały kierunek. Te obszary nazywamy domenami magnetycznymi.

Siła elektromotoryczna ( w skrócie SEM ) jest miarą wyrażoną w

Woltach. Nie jest ona siłą w sensie fizycznym od kiedy słowo "siła" nabrało w fizyce szczególnego

znaczenia. Nazwa jest swoistą pozostałością historyczną.

Źródłami siły elektromotorycznej SEM są np. generatory, baterie. Następuje w nich zamiana energii

Chemicznej lub mechanicznej na energię elektryczną.

Zjawisko siły elektromotorycznej Faradaya polega na wytwarzaniu siły elektromotorycznej w pętli przewodnika, poruszającej się w polu magnetycznym.

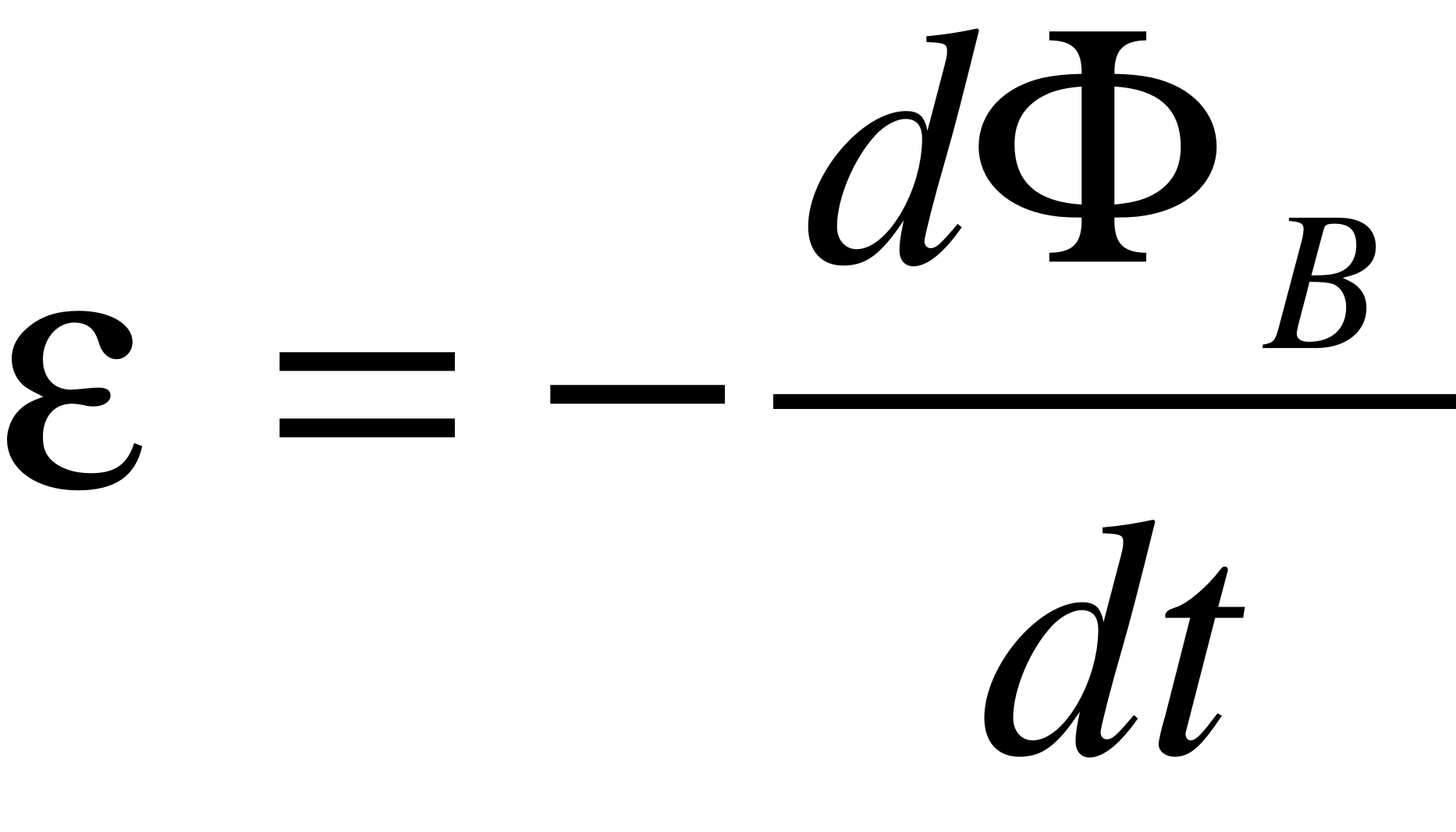
Gdzie:

- ε jest siłą elektromotoryczną,

- Φ jest strumieniem pola magnetycznego zdefiniowanego jako:

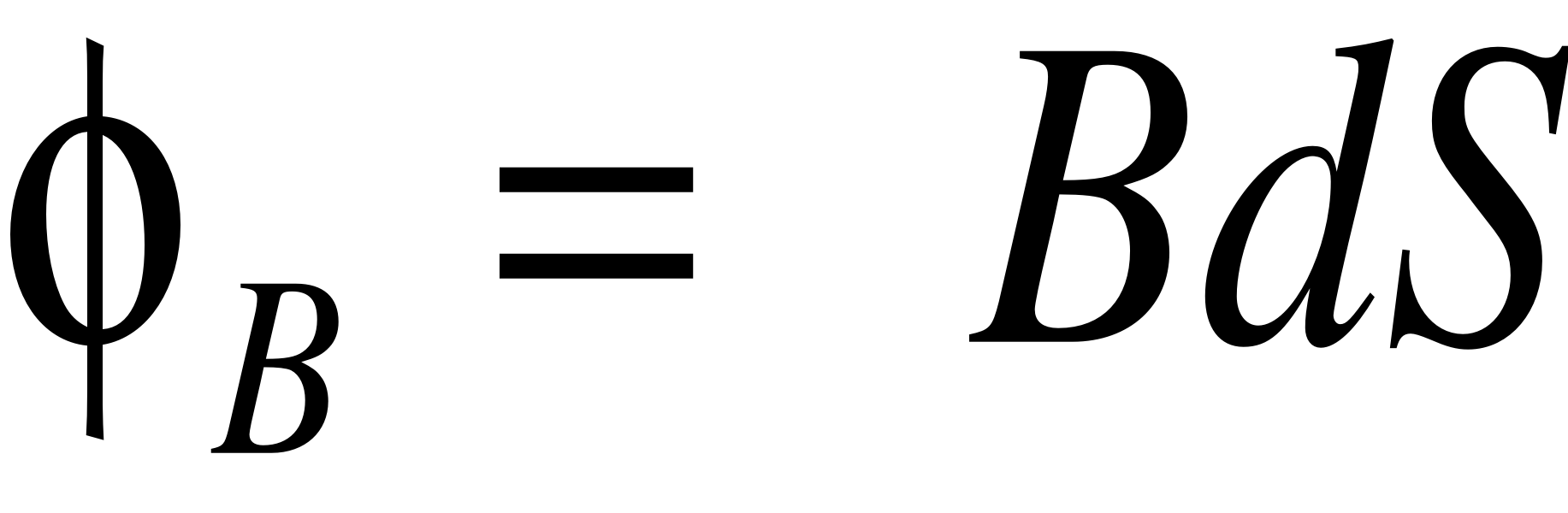
Gdzie:

- B jest indukcją pola magnetycznego,

- ds jest elementem powierzchni pętli.

Siła elektromotoryczna zależy od szybkości zmian strumienia: jeśli jest duży, siła elektromotoryczna jest również duża. Sposoby zmiany strumienia magnetycznego:

• zwiększyć indukcję magnetyczną lub powierzchnię czynną pętli przewodnika

• włączać i wyłączać elektromagnes

• włożyć w pętlę ferromagnetyk.

II Przebieg ćwiczenia:

1. Opis wykonywanych czynności:

W doświadczeniu korzystaliśmy z układu pomiarowego przedstawionego na rysunku poniżej.. W jego skład wchodzą:

- obracający się magnes

- dwie cewki

Układ pomiarowy umożliwia pomiary wpływu rdzenia ferromagnetycznego cewki na wielkość SEM, a także pomiary wpływu liczby zwojów.

Wpływ rdzenia ferromagnetycznego mierzyliśmy na zatrzaskach a i b: do tych zacisków podczas pomiaru był podłączamy amperomierz. Następnie rozpoczynamy obracanie magnesu i za pomocą amperomierza notowaliśmy wielkość siły elektromotorycznej. Pomiary były prowadzone gdy rdzeń był:

- cały włożony

- w połowie włożony

- wyciągnięty.

W celu zaobserwowania wpływu różnej liczby zwojów na indukowaną siłę elektromotoryczną używaliśmy zacisków c-d, d-e i c-e. Zaciski te podłączone są do drugiej cewki i obejmują albo całą cewkę (c-e), albo jej fragment (c-d, d-e),

Niekiedy zdarzało się, że wskaźnik wychodzi poza skalę przyrządu. Oznaczało to, że prąd, który przez niego przepływa jest zbyt duży. Należało go zatem ograniczyć. Standardowo w kablu amperomierza zainstalowany jest opornik 750Ω. Dodatkowo podłączyliśmy szeregowo do obwodu opornik 100k Ω

Każdy pomiar powtarzaliśmy 10 razy przy obrotach w rytmie:

- jednego obrotu na sekundę

- pięciu obrotów na sekundę.

2. Tabele wyników:

1 obr/s
Lp.	ED (z opornikiem 100 kΩ) [μA]	DC (z opornikiem 100 kΩ) [μA]	EC (z opornikiem 100 kΩ) [μA]	AB rdzeń wsunięty do połowy (z opornikiem 100 kΩ) [μA]	AB rdzeń wsunięty cały (z opornikiem 100 kΩ) [μA]	AB bez rdzenia (z opornikiem 100 kΩ) [μA]
1.	1,25	0,25	2,5	0,5	3,5	0,25
2.	1,5	0,3	2,25	0,5	3,5	0,25
3.	1,5	0,25	2,25	0,4	3	0,3
4.	1,25	0,2	2,5	0,5	3	0,3
5.	1,4	0,2	2,5	0,4	3,5	0,25
6.	1,5	0,3	2,5	0,4	3,25	0,4
7.	1,4	0,25	2,25	0,3	3,5	0,3
8.	1,25	0,25	2,25	0,5	3,5	0,4
9.	1,5	0,3	2,5	0,5	3,75	0,4
10.	1,5	0,2	2,25	0,4	3,5	0,4
Średnia	1,41	0,25	2,38	0,44	3,40	0,33
Odchylenie standardowe	0,11	0,04	0,13	0,07	0,24	0,07

5 obr/s
Lp.	ED (z opornikiem 100 kΩ) [μA]	DC (z opornikiem 100 kΩ) [μA]	EC (z opornikiem 100 kΩ) [μA]	AB rdzeń wsunięty do połowy (z opornikiem 100 kΩ) [μA]	AB rdzeń wsunięty cały (z opornikiem 100 kΩ) [μA]	AB bez rdzenia (z opornikiem 100 kΩ) [μA]
1.	1,5	0,2	2	0,5	4	0,25
2.	1,5	0,25	2,25	0,5	3,5	0,5
3.	1,5	0,2	2,25	0,75	4	0,5
4.	1,75	0,15	2	0,75	4	0,6
5.	1,5	0,2	2	0,75	4,5	0,6
6.	1,75	0,2	2,25	0,5	4	0,5
7.	1,75	0,15	2	0,5	3,5	0,6
8.	1,5	0,15	2	0,75	4	0,5
9.	1,75	0,25	2	0,5	4	0,5
10.	1,5	0,2	2,25	0,5	4	0,5
Średnia	1,60	0,20	2,10	0,60	3,95	0,51
Odchylenie standardowe	0,13	0,04	0,13	0,13	0,28	0,10

3. Obliczenia

- opornik w kablu - 750 Ω ,

- opornik dodatkowy - 100 kΩ = 100000 Ω, stosowany we wszystkich połączeniach

- Średnica cewki: 4,1 cm = 0,041m

- Długość cewki: 5,0cm = 0,05m

• Obliczanie wartości siły elektromotorycznej:

Dzięki temu, że:

ε = U

siłę elektromotoryczną można obliczyć korzystając z prawa Ohma:

po przekształceniu:

U = I * R [ΩּA = V]

R = 100750 - stosowany we wszystkich połączeniach.

I - zależne od połączenia, do wzoru podstawiliśmy wartości uśrednione z 10 pomiarów.

1 obr/s
Lp.	ED (opornik 100 kΩ) [μA]	DC (opornik 100 kΩ) [μA]	EC (opornik 100 kΩ) [μA]	AB rdzeń wsunięty do połowy (opornik 100 kΩ) [μA]	AB rdzeń wsunięty cały (opornik 100 kΩ) [μA]	AB bez rdzenia (opornik 100 kΩ) [μA]
Średnie: U = ε [V]	0,14	0,03	0,24	0,04	0,34	0,03

5 obr/s
Lp.	ED (opornik 100 kΩ) [μA]	DC (opornik 100 kΩ) [μA]	EC (opornik 100 kΩ) [μA]	AB rdzeń wsunięty do połowy (opornik 100 kΩ) [μA]	AB rdzeń wsunięty cały (opornik 100 kΩ) [μA]	AB bez rdzenia (opornik 100 kΩ) [μA]
Średnie: U = ε [V]	0,16	0,02	0,21	0,06	0,40	0,05

• Wielkość pola magnetycznego „B” wewnątrz cewki z rdzeniem:

- Średnica cewki z rdzeniem: 4,1 cm = 0,041m

- Długość cewki z rdzeniem: 5,0cm = 0,05m

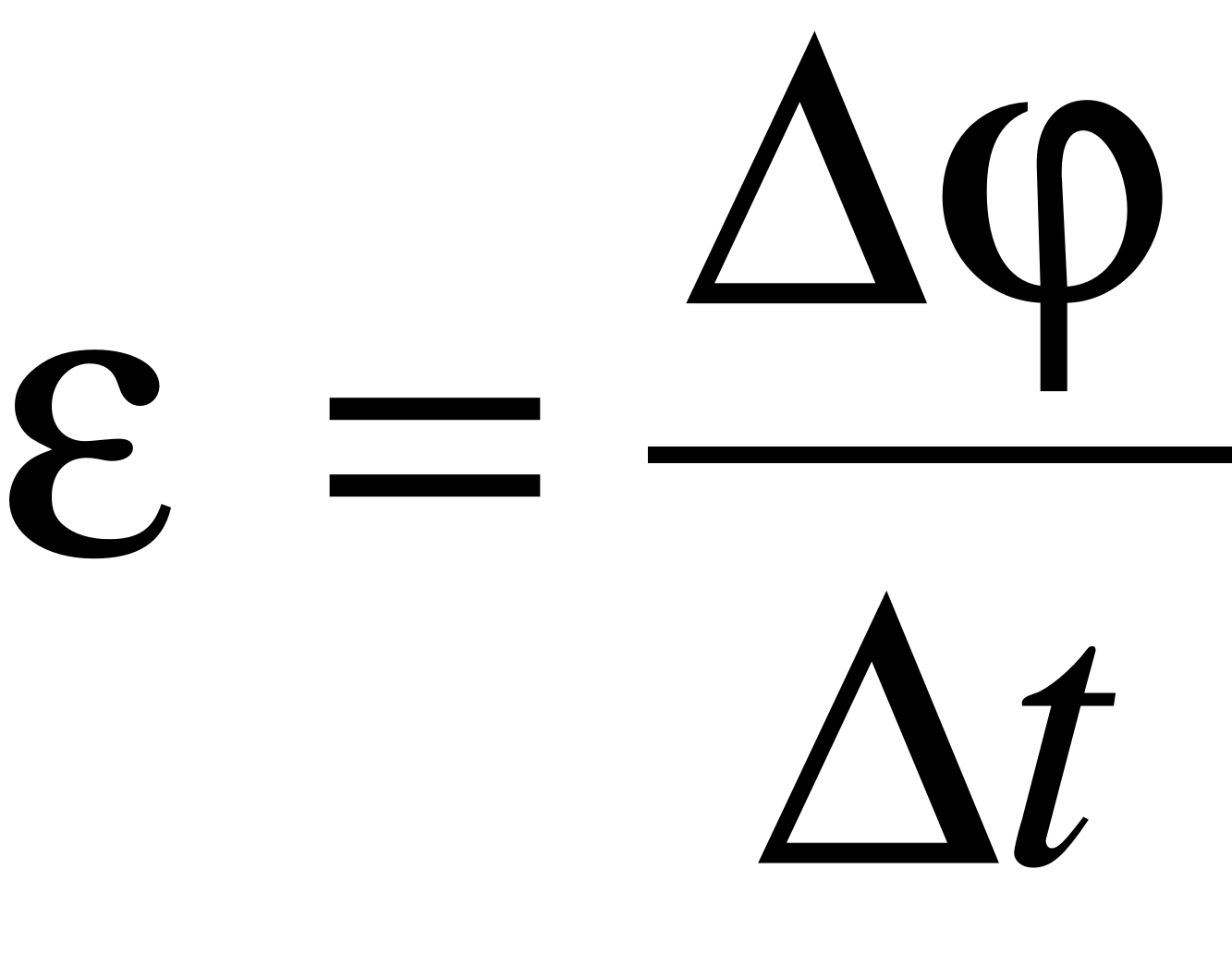
Δφ = BS

Gdzie:

ε - siła elektromotoryczna

Δφ- strumień pola magnetycznego

B - indukcja pola magnetycznego

S - zamknięta powierzchnia przecinająca pole magnetyczne

r = (4,1 cm/2)/100= 0,0205 m - średnica cewki z rdzeniem

Δt = czas, w którym strumień zmienia się od maksimum do 0

Ostateczny wzór:

Zmiana strumienia od maksimum do zera, co jest temu powodem?

Strumień jest iloczynem skalarnym wektorów B i S, więc zależy on od cosinusa kąta, pomiędzy tymi wektorami. Cosinus osiąga wartość 0 dla kąta π/2, a maksymalny jego okres to 2π.

W naszym ćwiczeniu obracaliśmy szybkością: 5 obr/s oraz 1 obr/s.

Więc częstotliwość wynosi: 5 Hz oraz 1 Hz, więc T wynosi odpowiednio: 0,2 oraz 1

Ponieważ podczas obrotu strumień czterokrotnie zmienia się od maksimum do minimum, wiec dzielimy to przez 4 co daje:

- dla 5 obr/s => Δt= 0,05s

- dla 1 obr/s => Δt= 0,25s

1 obr/s
	ED (opornik 100 kΩ) [μA]	DC (opornik 100 kΩ) [μA]	EC (opornik 100 kΩ) [μA]	AB rdzeń wsunięty do połowy (opornik 100 kΩ) [μA]	AB rdzeń wsunięty cały (opornik 100 kΩ) [μA]	AB bez rdzenia (opornik 100 kΩ) [μA]
Średnie: B [T]	26,82	4,77	45,33	8,40	64,90	6,20

5 obr/s
	ED (opornik 100 kΩ) [μA]	DC (opornik 100 kΩ) [μA]	EC (opornik 100 kΩ) [μA]	AB rdzeń wsunięty do połowy (opornik 100 kΩ) [μA]	AB rdzeń wsunięty cały (opornik 100 kΩ) [μA]	AB bez rdzenia (opornik 100 kΩ) [μA]
Średnie: B [T]	6,11	0,74	8,02	2,29	15,08	1,93

4. Analiza błędów

• Dla natężenia - za pomocą odchylenia standardowego:

1 obr/s
	ED (z opornikiem 100 kΩ) [μA]	DC (z opornikiem 100 kΩ) [μA]	EC (z opornikiem 100 kΩ) [μA]	AB rdzeń wsunięty do połowy (z opornikiem 100 kΩ) [μA]	AB rdzeń wsunięty cały (z opornikiem 100 kΩ) [μA]	AB bez rdzenia (z opornikiem 100 kΩ) [μA]
Odchylenie standardowe:	0,11	0,04	0,13	0,07	0,24	0,07

5 obr/s
	ED (z opornikiem 100 kΩ) [μA]	DC (z opornikiem 100 kΩ) [μA]	EC (z opornikiem 100 kΩ) [μA]	AB rdzeń wsunięty do połowy (z opornikiem 100 kΩ) [μA]	AB rdzeń wsunięty cały (z opornikiem 100 kΩ) [μA]	AB bez rdzenia (z opornikiem 100 kΩ) [μA]
Odchylenie standardowe:	0,13	0,04	0,13	0,13	0,28	0,10

• Dla napięcia - przy użyciu metody różniczki zupełnej:

U = ε

dU = I * dR + R * dI

R - nie zmienia się.

1 obr/s
	ED (opornik 100 kΩ) [μA]	DC (opornik 100 kΩ) [μA]	EC (opornik 100 kΩ) [μA]	AB rdzeń wsunięty do połowy (opornik 100 kΩ) [μA]	AB rdzeń wsunięty cały (opornik 100 kΩ) [μA]	AB bez rdzenia (opornik 100 kΩ) [μA]
dU	0,012	0,004	0,013	0,007	0,024	0,007

5 obr/s
	ED (opornik 100 kΩ) [μA]	DC (opornik 100 kΩ) [μA]	EC (opornik 100 kΩ) [μA]	AB rdzeń wsunięty do połowy (opornik 100 kΩ) [μA]	AB rdzeń wsunięty cały (opornik 100 kΩ) [μA]	AB bez rdzenia (opornik 100 kΩ) [μA]
dU	0,013	0,004	0,013	0,013	0,029	0,010

• Pola magnetycznego - przy użyciu metody różniczki zupełnej:
  

Gdzie:

d
= dU

dt = 0,01 [s]

dS = 10^-6 [m²]

1 obr/s
	ED (opornik 100 kΩ) [μA]	DC (opornik 100 kΩ) [μA]	EC (opornik 100 kΩ) [μA]	AB rdzeń wsunięty do połowy (opornik 100 kΩ) [μA]	AB rdzeń wsunięty cały (opornik 100 kΩ) [μA]	AB bez rdzenia (opornik 100 kΩ) [μA]
dB	3,27	0,97	4,36	1,68	7,26	1,55

5 obr/s
	ED (opornik 100 kΩ) [μA]	DC (opornik 100 kΩ) [μA]	EC (opornik 100 kΩ) [μA]	AB rdzeń wsunięty do połowy (opornik 100 kΩ) [μA]	AB rdzeń wsunięty cały (opornik 100 kΩ) [μA]	AB bez rdzenia (opornik 100 kΩ) [μA]
dB	1,72	0,29	2,10	0,95	4,11	0,77

5. Wyniki końcowe:

1 obr/s
	ε [V]	B [T]	I [μA]
ED	0,14 ± 0,012	26,82 ± 3,27	1,41 ± 0,11
DC	0,03 ± 0,004	4,77 ± 0,97	0,25 ± 0,04
EC	0,24 ± 0,013	45,33 ± 4,36	2,38 ± 0,13
AB (Rdzeń w połowie wsunięty)	0,04 ± 0,007	8,40 ± 1,68	0,44 ± 0,07
AB (Rdzeń cały wsunięty)	0,34 ± 0,024	64,90 ± 7,26	3,4 ± 0,24
AB (Bez rdzenia)	0,03 ± 0,007	6,20 ± 1,55	0,33 ± 0,07

5 obr/s
	ε [V]	B [T]	I [μA]
ED	0,16 ± 0,013	6,11 ± 1,72	1,6 ± 0,13
DC	0,02 ± 0,004	0,74 ± 0,29	0,2 ± 0,04
EC	0,21 ± 0,013	8,02 ± 2,1	2,1 ± 0,13
AB (Rdzeń w połowie wsunięty)	0,06 ± 0,013	2,29 ± 0,95	0,6 ± 0,13
AB (Rdzeń cały wsunięty)	0,4 ± 0,029	15,08 ± 4,11	3,95 ± 0,28
AB (Bez rdzenia)	0,05 ± 0,01	1,93 ± 0,77	0,51 ± 0,01

III Wnioski

• Przeprowadzając doświadczenie mogliśmy obserwować wpływ różnych czynników na wartość uzyskanego napięcia, czyli siły elektromotorycznej.

• Najbardziej widoczna była zmiana wartości napięcia podczas obecności w cewce rdzenia ferromagnetycznego lub jego brak. Włożony do połowy powodował zwiększenie indukcji pola. Natomiast po całkowitym wsunięciu rdzenia, indukcja pola wzrosła aż kilkunastokrotnie. Związane jest to z magnetyzowaniem się rdzenia w polu magnetycznym i dodatkowa indukcja pochodzi właśnie od rdzenia.

• Na ilość indukowanej SEM duży wpływ ma również ilość zwojów jak i odległość cewki od pola magnetycznego. Im więcej występowało zwojów tym SEM była większa. Wzrost wartości SEM obserwujemy również gdy cewka znajdzie się bliżej pola magnetycznego.

• Podczas ćwiczenia wyniki pomiarów zapisywaliśmy dla 1 obr/s oraz 5 obr/s. Tutaj również występują różnice w wartości SEM. W ćwiczeniu z obecnością ferromagnetyku dla 5 obs/s SEM była większa niżeli dla 1 obr/s co jest zgodne ze zdrowym rozsądkiem. Niestety w ćwiczeniu z wykorzystaniem cewki wyniki nie są już tak oczywiste. Jedynie w połączeniu E-D przy 5 obr/s wartość SEM była większa, natomiast w pozostałych dwóch połączeniach SEM była większa dla 1 obr/s

• Podczas przeprowadzania ćwiczenia narażeni byliśmy na liczne błędy pomiarów. Głównym powodem błędu były wskazania amperomierza, wskazówka podczas pomiarów była bardzo niestabilna, co utrudniało odczytanie natężenia. Kolejnym trudnością było tempo obrotów. Dosyć ciężko było utrzymać tempo 5 obr/s i to powodowało kolejne błędy. Błędy mogły również wynikać z niedokładności:

- stopera - podczas odmierzania czasu;

- linijki - podczas pomiaru średnicy cewki.

---