WYDZIAŁ MECHANICZNY |
IMIĘ I NAZWISKO
Wojciech Wszołek |
ZESPÓŁ 6 |
OCENA OSTATECZNA |
GRUPA 211c |
TYTUŁ ĆWICZENIA
Siatka dyfrakcyjna |
NUMER ĆWICZENIA 28 |
DATA WYKONANIA 24.10.2005 |
Wprowadzenie teoretyczne:
Siatka dyfrakcyjna to układ N wzajemnie równoległych i rozmieszczonych w równych odstępach szczelin. Odległość d środków sąsiednich szczelin nazywamy stalą siatki. Jeżeli na siatkę pada równoległa wiązka światła monochromatycznego o długości λ, to każda szczelina będzie źródłem pęku promieni ugiętych pod różnymi kątami. Otrzymany rozkład natężenia światła na ekranie jest podobny do obrazu otrzymanego w przypadku dwóch szczelin i składa się z serii prążków interferencyjnych, których względne natężenie modulowane jest przez obraz dyfrakcyjny pojedynczej szczeliny.
Promienie, wychodzące ze wszystkich szczelin i tworzące z pierwotnym kierunkiem kąt α, będą się wzajemnie wzmacniały, gdy różnica dróg δ między dwoma sąsiednimi ugiętymi promieniami równa jest wielokrotności długości fali:
δ=dsinαn=nλ, n=0,1,2,3,...
Równanie to określa położenie maksimów głównych natężenia światłą. Oznacza to, że odległość kątowa prążków jest określona stosunkiem λ/d i nie zależy od liczby szczelin N. Dla n=0 otrzymujemy prążek zerowy odpowiadający wiązce nieugiętej, dla n=1,2,...,k otrzymujemy prążki ugięte pierwszego, drugiego, k-rzędu. Jeżeli padające światło jest mieszaniną gal o różnych długościach, to położenia maksimów natężenia odpowiadają różnym kątom αn. Każdy rząd rozciąga się w widmo pierwszego, drugiego, n-tego rzędu. Liczba otrzymywanych rzędów jest ograniczona stałą siatki d, zgodnie z warunkiem nλ/d≤1
Dyspersja kątowa siatki jest miarą odległości kątowej dwu linii utworzonych przez dwie monochromatyczne fale, których długości różnią się od siebie o Δλ. Aby otrzymać dyspersję kątową różniczkujemy wyrażenie
![]()
Wielkość D=∂α/∂λ nazywamy dyspersją kątową siatki. Dyspersja wzrasta wraz z rzędem widma, natomiast jest odwrotnie proporcjonalna do stałej siatki d.
Zdolność rozdzielcza siatki jest miarą zdolności siatki do rozdzielenia dwóch blisko leżących linii widmowych. Siatka dyfrakcyjna pozwala rozróżnić dwie linie widmowe o długościach λ i λ+Δλ, jeżeli ich obrazy ugięciowe są tak rozsunięte, że główne maksimum fali o długości λ+Δλ występować będzie dla tego samego kąta, przy którym pojawi się pierwsze minimum linii drugiej, o długości λ(kryterium Rayleigha). Położenie maksimum linii λ+Δλ określa wzór:
dsinα`=n(λ+Δλ).
Ogólnie zdolność rozdzielcza siatki liczymy z:
![]()
Siatki dyfrakcyjne otrzymuje się przez nacinanie diamentowym ostrzem równoodległych, równoległych rys na szkle lub rowków na metalowej płycie
Wykonanie ćwiczenia:
Wyznaczenie stałej siatki ![]()
,korzystając ze wzorów:
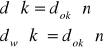
W naszym przypadku n=n', wiec wzór przyjmuje postać:
![]()
![]()
![]()
Zmieżone wartości:
n = 30
k = 26
k'= 13
dw=0,01mm
Podstawiamy wartości do wzoru:
![]()
= 0,005 mm
Obliczam niepewność maksymalną Δd
![]()
W naszym przypadku Δn'=Δn, i przyjmujemy 0,5 działki wiec wzór przyjmuje postać:
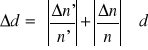
Obliczamy :
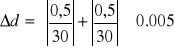
= 0,00016 mm
Wyznaczenie długości fali:
Tabela wyników przeprowadzonych pomiarów
L=450mm ΔL=1mm |
||||
Rząd widma n |
Barwa światła |
2yn mm |
yn±Δyn mm |
λ nm |
I |
Zielona |
99 |
49,5±0,5 |
546,7 |
II |
Zielona |
196 |
98±0,5 |
531,9 |
Dla badanego widma wyznaczamy zgodnie ze wzorem:
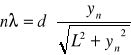
długość fali dla każdego rodzaju linii.
Rząd pierwszy n=1
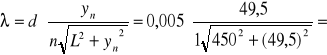
0,0005467 mm = 546,7 nm
Rząd drugi n=2
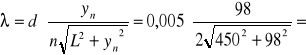
0,0005319 mm = 531,9 nm
Obliczam niepewność maksymalną Δλ metodą różniczki zupełnej dla barwy zielonej:
Obliczamy niepewności maksymalną metodą różniczki zupełnej:
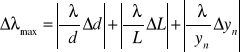
Licząc odpowiednio pochodne cząstkowe otrzymuję wzór:
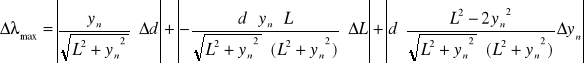
Do powyższego wzoru podstawiam otrzymane wartości dla n=2:
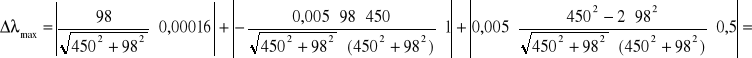
=0,0000340 + 0,00000225 + 0,00000469 = 0,00004094 mm = 40,94 nm
Ostateczny wynik:
λ=(531,9±40,94)nm
Wnioski:
W powyższym doświadczeniu największy wpływ na wynik końcowy miało wyznaczenie stałej siatki. Ponieważ niepewność pomiaru stałej siatki jest dość mała więc wnioskuję że została ona wyznaczona poprawnie. Poszczególne wartości barw widm mieszczą się w granicach podanych dla poszczególnych barw w tabelach stałych fizycznych.
d-stała siatki
![]()
-działka okulara
![]()
-wielkość działki mikrometrycznej skali wzorcowej
k -liczba rys siatki
![]()
- liczba działek skali wzorcowej
![]()
![]()
- liczby działek skali okularowej
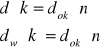
Wyszukiwarka
Podobne podstrony:
fizyka moje, cw14 2, WYDZIAŁ
fizyka moje, cw14 3, WYDZIAŁ
fizyka moje, cw13, Wydział Inżynierii Elektrycznej i Komputerowej
fizyka moje, cw17, Wydział Inżynierii Elektrycznej
TM10, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, Wydział Mechaniczn
05 h zaokrąglanie, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, Wydzi
podzielnice, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, Wydział Mec
04 Tech Zbiorcza, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, Wydzia
Ćwiczenie krzywki5, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, Wydz
cw20, Energetyka Politechnika Krakowska Wydział Mechaniczny I stopień, Fizyka, Laboratoria
TM9, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, Wydział Mechaniczny
TM1, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, Wydział Mechaniczny
Wydział Mechaniczno MOJE
Pytania i odpowiedzi FCS ost, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, S
cw16Misiek, Energetyka Politechnika Krakowska Wydział Mechaniczny I stopień, Fizyka, Laboratoria
05 a Karta obóbki cieplnej, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-mo
OBR BKA CIEPLNA, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, Wydział
notatka, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 2, StudiaII cz
więcej podobnych podstron