v1.5-Final 2004
W opracowaniu tym znajdują się 22 pytania (z wszystkich grup), jakie mieliśmy „przyjemność” dostać podczas sesji 2004 u prof. Kozielskiego.
Kto ma jakieś zielone pojęcie o tym przedmiocie niech poprawi te opracowanie (również treść pytań)
Moje opracowanie zawiera mało błędów ;-). Przemek
Rysunek przedstawia powierzchnie Gaussa w polu elektrycznym
. Sformułuj uogólnione prawo Gaussa i podaj, jaki jest strumień pola elektrycznego
dla kierunku pola
i
pokazanego na rysunku
Prawo Gaussa - strumień wektora indukcji pola o natężeniu
przechodzący przez dowolną (może być hipotetyczna) powierzchnię zamkniętą, jest równy całkowitemu ładunkowi zamkniętemu wewnątrz tej powierzchni.
Powierzchnia Gaussa - jest powierzchnią odzwierciedlającą rozkład geometryczny ładunku wewnątrz powierzchni
ΦE - liczba linii sił pola przypadającego na powierzchni
Prawo Gaussa:
ε0 - przenikalność elektryczna próżni
ΦE - strumień pola elektrycznego
ds - element powierzchni
q - ładunek
Napisz, jakie muszą być spełnione warunki powstania dobrze określonych prążków interferencyjnych w punkcie P
1° fale muszą być spójne (koherentne) tzn. muszą mieć stałe fazy w czasie i muszą mieć dokładnie określoną różnicę faz
2° d<<D
d - odległość między szczelinami
D - odległość szczelin od ekranu
3° wielkość szczeliny musi być rzędu długości fali d∼λ
nλ=dsinα
r2-r1= nλ - maksymalnie wzmocnione fale
r2-r1= (2n+1) λ/2 - maksymalnie osłabione fale
Uzupełnij wzory i zdefiniuj wielkości w niej występujące. Jakie wielkości fizyczne opisują te wzory?
|
|
Zależność promienia atomu od liczby kwantowej - kwantowa postać orbitalu elektronu
|
Zależność energii atomu od liczby kwantowej - kwantowa postać energii
|
|
|
n - główna liczba kwantowa h - stała Plancka 6,626*10-34 J*s ε0 - przenikalność elektryczna w próżni m - masa spoczynkowa elektronu 9,11*10-31 kg e - ładunek elementarny |
|
druga wersja tego pytania |
|
|
|
obliczyć energię jonizacji: energia jonizacji jest to wartość bezwzględna z energii dla liczby kwantowej 1 czyli po prostu Ej=13,6eV (eV-elektronoVolt) |
|
Trzecia wersja jest taka, że trzeba napisać te 2 wzory z głowy + napisać postulaty Bohra (pyt.11) |
|
Uzupełnij rysunek tak, aby przedstawiał falowy charakter ruchu elektronu na orbitalu. Udowodnij, że ten ruch spełnia odpowiedni postulat Bohra.
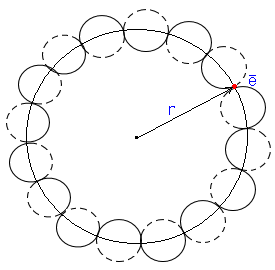
r - promień orbitalu elektronu
2πr - droga elektronu
2πr = nλ
postulat Bohra
h - stała Plancka
L - moment pędu elektronu
n - ilość fal na orbitalu
λ - długość fali
p - pęd cząsteczki
Można napisać ten postulat:
Elektron może poruszać się tylko po takim orbitalu, dla której moment pędu elektronu jest wielokrotnością stałej Plancka przez 2π
Sformułować zasadę zachowania energii cząstki relatywistycznej będącej w zewnętrznej energii potencjalnej.
Zasada zachowania energii cząstki relatywistycznej będącej w ruchu
E oznacza całkowitą energię ciała poruszającego się z prędkością v≠0 w polu sił potencjalnych U.
E=mc2+U=const
E=m0c2+(½m0v2+
+…)+U=const
E=m0c2+½m0v2+U dla małych prędkości
m - masa cząstki relawistycznej
c - prędkość światła
v - prędkość cząstki
U - energia potencjalna cząstki
Sprężyna - była narysowana sprężyna i napisać równanie siły wywołującej odchylenia i równanie różniczkowe dla rysunku. Napisać definicje siły F
Jest to ruch harmoniczny prosty
siła jest wprost proporcjonalna do wychylenia
Znak minus oznacza, że siła jest zawsze skierowana przeciwnie do wychylenia, czyli jest zawsze skierowana do położenia równowagi. Równanie różniczkowe ruchu harmonicznego prostego:
x - wychylenie
m - masa ciała
k - współczynnik sprężystości
Podaj ilość atomów w krysztale + opis
a) a1=a2=a3
α=β=γ=90°
b) a1≠a2≠a3
α=β=γ=90°
c) a1≠a2≠a3
α=γ=90°; β≠90°
8*1/8 + 6*½ = 1+3 = 4
8*1/8 + 1 = 1+1 = 2
8*1/8 + 2*½ = 1+1 = 2
1/8 - atom znajduje się w narożniku kryształu
1 - atom znajduje się w środku kryształu
½ - atom znajduje się w ścianie kryształu
Napisz co przedstawia rysunek.
Zasada zachowania momentu pędu dla bryły sztywnej:
Gdy wypadkowy moment sił zewnętrznych działających na bryłę sztywną wynosi 0 to całkowity moment pędu bryły pozostaje stały.
W praktyce zasadę tą wykorzystują np. łyżwiarze - poprzez zmianę położenia rąk można zwiększyć prędkość kątową bez zwiększenia pędu.
Obliczyć moment bezwładności ciała. Podać, z jakiego twierdzenia to wynika oraz wypisać wszystkie wzory
Z twierdzenia Steinera I=I0+ma2
I - moment bezwładności ciała względem osi obrotu
a - odległością między osiami
gdzie r oznacza odległość elementu masy dm od osi obrotu
dm = ρdv = ρdxdydz
ρ- gęstość bryły
Jeżeli oznaczymy przez I0 moment bezwładności ciała względem osi 00' przechodzącej przez środek masy, to moment bezwładności ciała względem dowolnej osi AA' równoległej do osi przechodzącej przez środek masy leżącej w tej samej płaszczyźnie jest równy I=I0+ma2
Opisać składnie tego wzoru oraz podać sens fizyczny tego twierdzenia. Napisać co to jest m, ψ i U
|
+ |
|
= |
|
operator energii kinetycznej |
|
operator energii potencjalnej |
|
operator energii całkowitej |
Jest to równanie Schrödingera
ψ - funkcja falowa, która jest zależna od współrzędnych i czasu (x,y,z,t)
m - masa kwantu
Sensem fizycznym ogólnego równania Schrödingera jest zasada zachowania energii dla cząstek kwantowych
Jest to podstawowe równanie mechaniki kwantowej, prawo przyrody, którego nie trzeba udowadniać. Funkcja Schrödingera opisuje ruch cząsteczek i za jej pomocą można określić gęstość prawdopodobieństwa znalezienia cząstki w danej objętości. Funkcja Schrödingera zależy od warunków zewnętrznych - uwzględnione w równaniu gdy dodajemy przebieg energii potencjalnej.
Są dwie wersje tego pytania:
podany jest wzór - podpisać że jest to równanie Schrödingera
napisać równanie Schrödingera
Wymienić postulaty Bohra
- elektron nie może krążyć po dowolnym orbitalu, lecz tylko po takim orbitalu, dla których moment pędu elektronu L jest wielokrotnością stałej Plancka podzielonej przez 2π
- atom absorbuje energie lub emituje energie w postaci kwantu przechodząc z jednego stanu energetycznego atomu do drugiego
j>i - emisja
j<i - absorpcja
Udowodnij, że praca wykonana przez ciało jest równa zeru - napisać, jaka zachodzi zależność
Jest to zależność, w której zachodzi siła zachowawcza, ponieważ praca wykonana przez nią podczas ruchu między dwoma punktami zależy tylko od tych punktów, a nie od drogi łączącej te punkty.
W=0
W(A→B→C→D→E→F→G→A)=0
Druga wersja rysunku:
to jest kiepsko opracowane bo należy to obliczyć !
Uzupełnij rysunek i podpisz go?
Polaryzacja światła - polega na uporządkowaniu kierunków drgań wektorów pola elektrycznego
pola magnetycznego
. Dla wszystkich punktów fali drgający wektor elektryczny
leżący w płaszczyźnie XZ tworzy z kierunkiem ruchu fali płaszczyznę zwaną płaszczyzną drgań, a płaszczyzna drgań wektora magnetycznego
, który leży w płaszczyźnie YZ nazywa się płaszczyzna polaryzacji. Kierunek osi Z pokrywa się z kierunkiem prędkości rozchodzenia się fali
Zjawisko dwójłomności światła - kryształ podwójnie łamie wiązki padającej i powstaje rozszczepienie wiązki
Były kulki i jedne uderzały w drugie - jaka zasada - opisać
Zasada zachowania pędu dla układu punktów materialnych
Kiedy suma sił zewnętrznych działających na układ punktów materialnych wynosi zero, to całkowity pęd układu pozostaje stały.
Całkowity pęd układu może być zmieniony tylko przez siły zewnętrzne działające na układ. Siły wewnętrzne będące równymi i przeciwnie skierowanymi wytwarzają równe i przeciwnie skierowane zmiany pędu, które nawzajem się redukują. Pędy poszczególnych punktów układu mogą ulegać zmianom, ale suma tych pędów jest stała, jeżeli na układ nie działają żadne siły zewnętrzne:
Podpisać wykresy, wrysować wykres dla fizyki relatywistycznej, wypisać wzory + dodatkowy opis
|
Wykres zależności masy cząstki relatywistycznej w funkcji jej prędkości
|
|
Wykres zależności pędu cząstki relatywistycznej w funkcji jej prędkości
|
|
Wykres zależności energii cząstki relatywistycznej w funkcji jej prędkości
|
Podpisz poniższy rysunek, napisz co przedstawia i wypisz wszystkie wzory
Zjawisko Comptona:
Foton padając na elektron wybija go przekazuje mu tylko część swojej energii. W skutek tego foton zmienia kierunek ruchu (następuje tzw. rozproszenie Comptona), przy czym zmniejsza swoją energie, a zatem również częstość
m - masa elektronu
h - stała Plancka
c - prędkość światła
λ - długość fali
zasada zachowania energii |
Ee=m0c2(γ-1) |
|
zasada zachowania energii |
pe=m0vγ |
|
Przesunięcie Comptona:
- comptonowska długość fali elektronu
Uogólniona postać wzoru na Ep i Ek wychodząc z wzoru:
Energia kinetyczna:
Ek - energia kinetyczna
F - siła działająca na ciało powodująca jego ruch
F = ma
m - masa ciała
- przyspieszenie ciała
- prędkość ciała
Energia potencjalna:
- siła pola
np.
h - wysokość na której umieszczono ciało
g - grawitacja
Scharakteryzować, czym jest strefa Brilloulina + obliczyć jej objętość
Strefa Brilloulina - obszar, w którym energia funkcji wektora falowego jest ciągła, na granicy doznaje skoku
Przedziały wartości wektora k, w którym energia elektronu poruszającego się w krysztale zmienia się w sposób ciągły nazywamy strefami Brilloulina
Wszystkie Strefa Brilloulina są równe
więc chyba odpowiedź jest taka
I żółta strefa -
II jasnofioletowa strefa -
III ciemnofioletowa strefa -
Podpisać wykres energii kinetycznej i potencjalnej i jaka zasada tu zachodzi?
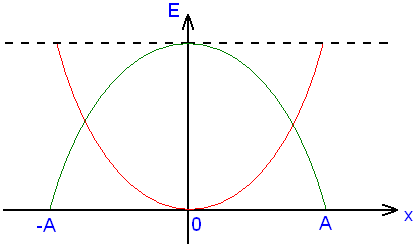
E=Kmax=Umax=½kA2
en. potencjalna
en. kinetyczna
Zasada zachowania energii mechanicznej oscylatora harmonicznego. Energia kinetyczna i energia potencjalna jako funkcje wychylenia z położenia równowagi
Masz rysunek przedstawiający dielektryk miedzy okładkami kondensatora i podpisać co jest co gdzie jest co i w jakich koligacjach. Są te dane wielkości, np. co to jest a?
Pytanie związane z pojęciem środka masy dla układu punktów materialnych.
Wykres potencjału hamowania elektronów w fotokomórce od częstotliwości padającego promieniowania i trzeba było napisać, co możemy z tego obliczyć i napisać wzory
Oryginalny rysunek w pytaniu |
Chyba dobra odpowiedź |
|
|
Trzeba zauważyć, że rysunek na egzaminie troche się różni od tego który jest w książce prof. Kozielskiego |
|
|
|
ładunek zewnętrzny |
|
|
powierzchnia |
|
|
stała dielektryczna |
|
|
przenikalność elektryczna próżni |
|
|
ładunek indukowany |
|
|
powierzchnia |
Środkiem masy układu N punktów materialnych nazywamy punkt s, gdy jego współrzędne w przestrzeni wynoszą:
gdzie:
xs, ys, zs - odległości od punktu 0 układu odniesienia
jest całkowitą masą układu punktów materialnych
Jest to prawo fotonowe Einsteina
|
E0 - praca wyjścia elektronu na powierzchnie metalu Kmax - energia kinetyczna elektronu po opuszczeniu metalu V0 - potencjał hamujący e - ładunek
|
Jeżeli wykonany doświadczalnie pomiar zależności V0() i wykreślimy zależność potencjału hamującego V0 w funkcji , to tangens nachylenia tej krzywej w stosunku do osi pozwala wyznaczyć stałą Plancka h=etg
- matematyka
GrupaB4.prv - 2004 Anetka, Przemek, jaś i Kaś oraz Ewek + Łukasz z B2
Wyszukiwarka
Podobne podstrony:
PO wyk07 v1
s10 v1
s7 4 v1
s9 3a v1
Prezentacja v1
2 BO 2 1 PP Przykłady Segregator [v1]
Notice V1
BoeBot v1 0 id 91312 Nieznany (2)
19 Podwykonawcy i dostawcy v1 1id 18332
gmm v1 streszczenie
Omron Przewodnościowy regulator poziomu cieczy 61F D21T V1
Odpowiedzi correct v1
spraw4 waga v1
cwN10 oporliniowy v1 2 (3)
Staw Kolanowy v1 2
NOO K1 sc v1
więcej podobnych podstron