Właściwości magnetyczne - Efekt Curie

Ze względu na zachowanie magnetyczne (to znaczy na to w jaki sposób substancja reaguje na pole magnetyczne) materiały dzielimy na diamagnetyki, paramagnetyki, ferromagnetyki, anty-ferromagnetyki. Jest to podział najbardziej podstawowy.

Zanim omówimy własności magnetyczne poszczególnych grup materiałów musimy sobie przypomnieć kilka prostych faktów dotyczących budowy atomu. Pamiętamy (a może nie pamiętamy, jeśli tak jest to zachęcam do przeczytania mojego wykładu pt. „Podstawy budowy atomu”), że elektron możemy opisywać za pomocą czterech liczb kwantowych.:

• Głównej liczby kwantowej

• Kwantowej liczby krętu orbitalnego czasami nazywaną orbitalną liczbą kwantową

• Magnetycznej liczby kwantowej

• Spinowej liczby kwantowej

Te cztery powyższe liczby składają się na tzw. stan elektronu. Mówiąc najprościej wybieramy sobie elektron i przyporządkowujemy mu cztery liczby, które opisują jego właściwości. To tak jak byśmy poszli do sklepu meblowego znaleźli szafkę o nazwie „Elektron” i przyporządkowali jej wysokość, długość, szerokość oraz materiał z jakiego została wykonana. Tak samo liczby kwantowe opisują elektron.

Skupimy się teraz na orbitalnej liczbie kwantowej. Liczba ta wpływa na wartość tzw. orbitalnego momentu pędu, który opisany jest ogólnym wzorem:

(1.0 a)

gdzie l- orbitalna liczba kwantowa,
-stała Plancka kreślona

Do opisu zjawisk magnetycznych jednak możliwe jest użycie modelu Bohra, w którym elektron poruszał się po orbitach kołowych. Nie musimy zatem stosować wzoru (1.0a) ponieważ możemy zastosować wzór (1.0 b) pamiętając jednocześnie, że wartości momentu pędu nie są dowolne lecz skwantowane co wynika z II postulat Bohra.

(1.0 b)

gdzie v- prędkość elektronu, m- masa elektronu r- promień wodzący

Z istnienia tego orbitalnego momentu pędu (czyli po prostu z ruchu elektronu po orbicie) wynika istnienie orbitalnego momentu magnetycznego, który powiązany jest z orbitalnym momentem pędu poniższą zależnością:

(1.1)

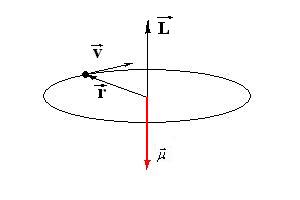
gdzie e- ładunek elektronu, m- masa elektronu, L - orbitalny moment pędu

Na podstawie wzoru (1.0 b) widać, że wektor orbitalnego momentu pędu jest prostopadły do płaszczyzny orbity elektronu. Patrząc na wzór (1.1) widzimy, że wektor orbitalnego momentu magnetycznego też jest prostopadły do płaszczyzny orbity elektronu, jednak jego zwrot jest przeciwny. Możemy zatem powiedzieć, że wektory orbitalnego momentu magnetycznego i orbitalnego momentu pędu są antyrównoległe.

Udowodniono jednak, że poza orbitalnym momentem pędu i orbitalnym momentem magnetycznym elektron posiada własne momenty pędu. Posiada on :

• własny moment pędu nazywany spinem:

Już na wstępie należy powiedzieć, że spin pomimo, że nazywany jest własnym momentem pędu nie może być utożsamiany z obrotem elektronu. Początkowo fizycy zakładali obrót elektronu wokół własnej osi- obrót taki jednak nie istnieje, a model taki prowadzi do powstania licznych sprzeczności. Spin zatem należy traktować jako pewną cechę elektronu taką samą jak masa czy ładunek.

Spin w przypadku elektronu może przyjmować jedynie dwie wartości.

(1.2)

Jest to bezpośrednio związane z wartością spinowej liczby kwantowej, dlatego też równanie (1.2) możemy zapisać nieco inaczej :

(1.3)

gdzie s- spinowa liczba kwantowa, która przyjmuje wartości +1/2 lub -1/2

• oraz spinowy moment magnetyczny

Który związany jest bezpośrednio z własnym momentem pędu (czyli spinem) zależnością:

(1.4)

Widzimy zatem, że spinowy moment magnetyczny jest skierowany przeciwnie do własnego momentu pędu (spinu). Wektory spinowego momentu magnetycznego i własnego momentu pędu (spinu) są antyrównoległe. Widzimy zatem pewną analogię pomiędzy momentami orbitalnymi (czyli orbitalnym momentem pędu i orbitalnym momentem magnetycznym), a własnymi momentami elektronu (czyli spinowym momentem magnetycznym oraz własnym momentem pędu [spinem] ). Również widzimy, że zależność (1.1) oraz (1.4) są bardzo podobne, a różnią się jedynie współczynnikiem ½ .

Podsumujmy zatem. Elektron posiada:

• orbitalny moment pędu, na który „wpływa” orbitalna liczba kwantowa, (związany z ruchem po orbicie)

• orbitalny moment magnetyczny związany z istnieniem ruchem elektronu po orbicie czyli orbitalnym momentem pędu.

• własny moment magnetyczny czyli spin

• spinowy moment magnetyczny związany ze spinem

Wszystkie te cztery wielkości fizyczne są wektorami. Przypomnijmy, że wektory orbitalnych momentów (czyli orbitalnego momentu pędu jak i orbitalnego momentu magnetycznego) są wzajemnie antyrównoległe (czyli przeciwnie skierowane) jak i własne momenty magnetyczne elektronu (czyli własny moment magnetyczny oraz spinowy moment magnetyczny) również są wzajemnie antyrównoległe.

Jednak przez cały czas mówimy o elektronach. Można zapytać, zatem co z jądrem atomowym. Przecież jądro atomu składa się z protonów i neutronów, które powinny też posiadać spin i własne momenty magnetyczne, no i faktycznie tak jest. Zarówno protony jak i neutrony posiadają wewnętrzne momenty magnetyczne jednak w porównaniu z wewnętrznymi momentami magnetycznymi elektronów są one bardzo małe i można je pominąć.

No dobrze. Ustaliliśmy, więc że jądro atomowe posiada znikome momenty magnetyczne zatem możemy je pominąć. Poza tym elektron posiada cztery rodzaje momentów (dwa orbitalne i dwa własne). No dobrze ale przecież w samym atomie jest kilka, kilkanaście bądź kilkadziesiąt elektronów. Co więc z tym zrobić. Problem z punktu widzenia teoretycznego jest dość prosty, ponieważ wszystkie momenty tak orbitalne jak i magnetyczne są wektorami. Wystarczy, zatem wszystkie te momenty zsumować w wyniku czego otrzymamy jakiś wektor wypadkowy. Weźmy pod uwagę orbitalny moment pędu elektronu. Suma wszystkich wektorów orbitalnych momentów pędu ma postać:

(1.5)

gdzie
- orbitalny moment pędu atomu, N- liczba elektronów w atomie
- orbitalny moment pędu i-tego elektronu.

Przypadek orbitalnego momentu magnetycznego jest analogiczny. Suma wektorów jest równa:

(1.6)

gdzie
- orbitalny moment magnetyczny atomu, N- liczba elektronów w atomie,
-orbitalny moment magnetyczny i-tego elektronu.

Należy zwrócić tutaj uwagę na fakt iż sumujemy wektory a nie wartości orbitalnego momentu magnetycznego. W efekcie otrzymujemy jakiś wypadkowy wektor, którym będziemy się zajmować w dalszej części wykładu.

Wiedząc już to wszystko możemy przejść do omawiania własności magnetycznych substancji.

Diamagnetyki

I tutaj na czytelnika przynajmniej na początku czeka małe zaskoczenie ponieważ diamagnetyki pola magnetycznego nie wytwarzają. No ale jak to się ma do tego co mówiliśmy wcześniej. Od dłuższego czasu wysilamy się na tłumaczenie, że w elektronach występują jakieś momenty magnetyczne są jakoś ustawione no i co. Otóż wszystko się zgadza elektrony posiadają momenty magnetyczne. Momenty te są niezerowe ale tylko w obrębie elektronu, ewentualnie atomu, ale gdy patrzymy na substancję z „zewnątrz” nie wykazuje ona namagnesowania ponieważ momenty magnetyczne się zniosą. Gdy wysumujemy wszystkie momenty magnetyczne (które są przecież wektorami) pochodzące od poszczególnych atomów okaże się, że wektor wypadkowy jest zerowy. Dzieje się tak dlatego, że momenty magnetyczny, ustawione są chaotycznie i choć niezerowe w przypadku poszczególnych cząstek, atomów czy elektronów, wzajemnie się znoszą.

Spróbujmy jednak teraz diamagnetyk umieścić w zewnętrznym polu magnetycznym
. Popatrzmy co dzieje się teraz z elektronem. Na jego orbitę działa moment siły, który wymusza ustawienie się orbitalnego momentu magnetycznego wzdłuż kierunku pola magnetycznego
., a orbitalnego momentu pędu elektronu w kierunku przeciwnym. Dlaczego? Prawie każdy z nas widział kiedyś dziecinną zabawkę jaką jest bąk. Kiedy wprawimy go w ruch jego oś wokół której się obraca jest mniej więcej prostopadła do podłoża. Wystarczy jednak niewielka siła, a konkretnie moment siły, aby po jakimś czasie oś jego zaczęła ulegać precesji wokół pierwotnego położenia osi. Tak samo dzieje się w przypadku elektronu. Zewnętrzne pole magnetyczne powoduje wytworzenie się momentu siły, który wymusza precesję orbity elektronu. Ponieważ jednak wektory orbitalnego momentu pędu oraz orbitalnego momentu magnetycznego są prostopadłe do powierzchni orbity, również i one ulegają precesji. Można udowodnić, że płaszczyzna orbity elektronu ulega precesji z tzw. częstością Larmora opisaną wzorem:

(1.7)

Jak widzimy częstość Larmora (prędkość kątowa) nie zależy ani od kąta pomiędzy płaszczyzną orbity a liniami pola magnetycznego ani od prędkości elektronu ani też od promienia jego orbity. Częstość ta jest zatem jednakowa dla wszystkich elektronów znajdujących się w danej materii (poddanej jednorodnemu polu magnetycznemu). Z powodu precesji jednak elektron porusza się po innym torze w wyniku czego następuje wyindukowanie się dodatkowego prądu, któremu odpowiada tzw. wyindukowany wymuszony moment magnetyczny. Zwrot tego momentu jest przeciwny do zewnętrznego pola magnetycznego
w wyniku czego następuje osłabienie tego pola.

Precesja ta zwana jest precesją Larmora.

- orbitalny moment pędu

- orbitalny moment magnetyczny

- moment siły

- wyindukowany (wymuszony orbitalny moment magnetyczny

Podsumujmy zatem. Dielektryk nie znajdujący się w polu magnetycznym nie posiada własnego pola magnetycznego, ponieważ jego momenty magnetyczne się wzajemnie znoszą. Gdy umieścimy go jednak w polu magnetycznym orbita elektronu ulega precesji w wyniku czego powstaje przeciwnie moment magnetyczny skierowany przeciwnie do pola zewnętrznego w wyniku czego obserwujemy osłabienie pola zewnętrznego.

Do dielektryków zaliczamy m. in. Gazy szlachetne, wodór, azot, NaCl.

Paramagnetyki

Zajmijmy się teraz paramagnetykami. Rozpocznijmy od spojrzenia na paramagnetyk, który nie znajduje się w żadnym zewnętrznym polu magnetycznym. Okazuje się, że jego wypadkowy moment magnetyczny nie jest równy zero. Najogólniej rzecz biorąc przyczyną niezerowego momentu magnetycznego jest odpowiednie ustawienie się orbitalnych jak i spinowych momentów magnetycznych. W paramagnetykach (tak jak i w dielektrykach) występuje precesja Larmora. Istnieje jednak pewna zasadnicza różnica. Ponieważ paramagnetyk posiada niezerowe momenty magnetyczne to w chwili umieszczenie go w zewnętrznym polu magnetycznym następuje porządkowanie się jego momentów magnetycznych, które ustawiają się zgodnie ze zwrotem zewnętrznego pola magnetycznego. Następuje wówczas wzmocnienie tego pola. W paramagnetykach (tak jak i w diamagnetykach) również indukuje się prąd, któremu odpowiada wyindukowany (wymuszony) moment magnetyczny. Zwrot tego momentu jest przeciwny do zwrotu pola jednak w porównaniu z uporządkowanymi momentami magnetycznymi ma bardzo mały wpływ na własności magnetycznego substancji. Na wzrost uporządkowania momentów magnetycznych wpływają także zderzenia atomów (cząsteczek) a co za tym idzie i temperatura.

Podsumowując zatem. Paramagnetyki posiadają niezerowe wypadkowe momenty magnetycznego, które po umieszczeniu w polu magnetycznym ulegają uporządkowaniu w wyniku czego wzmacniają zewnętrzne pole magnetyczne. Wyindukowane przeciwne pole magnetyczne jest mniejsze od pola powstałego z uporządkowania się momentów magnetycznych.

Względna podatność magnetyczna- Prawo Curie

Do opisu właściwości magnetycznych substancji wprowadza się bezwymiarową wielkość zwaną względną podatnością magnetyczną oznaczaną przez
. Zgodnie z prawem Curie (obowiązującym tylko dla paramagnetyków) istnieje ścisła zależność między podatnością magnetyczną, a temperaturą:

(1.8)

gdzie C- stała Curie, T - temperatura.

Ferromagnetyki

Jeśli chodzi o ferromagnetyki to sytuacja jest w nich nieco inna niż w paramagnetykach i diamagnetykach. Wewnątrz ferromagnetyków bowiem znajdują pewne niewielkie obszary (wielkości 1-10
m) w których występuje spontaniczne uporządkowanie momentów magnetycznych. Oznacza to, że w naszej substancji (ferromagnetyku) znajdują się nie pojedyncze elektrony, ale całe obszary, w których momenty magnetyczne są uporządkowane. Uporządkowanie to wynika z istnienia tzw. oddziaływań wymiennych pomiędzy elektronami. Oddziaływanie to jak udowodnił na drodze doświadczalnej J.G. Dorfman w 1927r. nie jest pochodzenia magnetycznego jak się można by spodziewać. Dorfman obserwował odchylenie elektronów przechodzących przez namagnesowaną folię niklową. Gdyby oddziaływania miały charakter magnetyczny odchylenie byłoby znaczne tymczasem obserwował on jedynie niewielkie zakrzywienia toru lotu elektronu. Oddziaływanie to ma charakter wyłącznie elektryczny.

Całkowity moment magnetyczny próbki ferromagnetyka jest sumą wektorów momentów magnetycznych poszczególnych domen. Do opisu stopnia namagnesowania próbki stosuje się wielość fizyczną zwaną właśnie namagnesowanie i oznaczać ją będziemy przez J. W ogólności namagnesowanie jest sumą wszystkich wektorów momentów magnetycznych pochodzących od danego elementu (np. atomu, elektronu, domeny) podzieloną przez objętość w jakiej te elementy się znajdują :

gdzie N- ilość elementów J- namagnesowanie,
- objętość
- moment magnetyczny i-tego elementu

Namagnesowanie ferromagnetyka (J) zależy od natężenia pola magnetycznego H w sposób złożony. Zazwyczaj już dla niewielkich natężeń pola magnetycznego namagnesowanie osiąga stan nasycenia, co widać na poniższym wykresie.

Zależność pomiędzy natężeniem pola, namagnesowaniem, a indukcją magnetyczną opisuje wzór.

(1.9)

gdzie H- natężenie pola magnetycznego, J - namagnesowanie, B - indukcja magnetyczna
-przenikalność magnetyczna próżni

Gdy już zostanie osiągnięty stan nasycenie to znaczy namagnesowanie jest stałe (J=const.) wówczas wzór (1.9) przechodzi we wzór (1.10). Jak widzimy indukcja magnetyczna rośnie liniowo - zależy tylko od natężenia pola.

(1.10 a)

(1.10 b)

Zależność indukcji magnetycznej przebiega w taki sposób jedynie w przypadku gdy próbka nie była namagnesowana wcześniej (dlatego właśnie wszelkie doświadczenia zależą od historii danej próbki ferromagnetyka). Gdy zaczniemy, bowiem zmniejszać natężenie pola magnetycznego indukcja pola magnetycznego zacznie maleć w zupełnie inny sposób nie będzie to już zależność liniowa i tak dla zerowego zewnętrznego pola, próbka nadal pozostanie namagnesowana. Krzywą pokazującą zależność indukcji B od natężenia H nazywamy krzywą (pętlą) histerezy. Gdy maksymalne natężenie jest takie, że namagnesowanie osiągnie nasycenie to mówimy o maksymalnej pętli histerezy. Gdy namagnesowanie nie osiągnęło nasycenia mówimy o cyklu cząstkowym.

Na powyższym rysunku widać, że do momentu osiągnięcia nasycenie

(to znaczy na odcinku OE) indukcja zmienia się w sposób skomplikowany po osiągnięciu nasycenie w punkcie E zależność (1.9) przechodzi w liniową zależność (1.10) co widać na odcinku EF. Jednak gdy po osiągnięciu stanu nasycenia w punkcie E nie będziemy dalej zwiększać natężenia pola magnetycznego H, a wręcz przeciwnie, zaczniemy je zmniejszać wówczas indukcja magnetyczna będzie przyjmowała wartości odpowiadające krzywej przechodzącej przez punkty E-G-I-A, czyli mówiąc kolokwialnie pójdzie górną drogą do punktu A. Zwróćmy teraz uwagę na ciekawą rzecz. Co dzieje się w punkcie G. Otóż w punkcie G natężenie pola magnetycznego jest zerowe czyli pola zewnętrznego działającego na ferromagnetyk nie ma. Okazuje się jednak, że nasza próbka ferromagnetyka wykazuje właściwości magnetyczne ponieważ indukcja magnetyczna B jest niezerowa!!. Pójdźmy jednak dalej. Dotarliśmy do punktu A. Zacznijmy teraz zwiększać natężenie pola magnetycznego. Wówczas indukcja magnetyczna B będzie przyjmowała wartości odpowiadające krzywej A-C-D-E. Zauważmy, że w punkcie C pola magnetycznego znów nie ma, a mimo to indukcja magnetyczna jest niezerowa. Tym razem jednak indukcja magnetyczna ma przeciwny zwrot w stosunku do indukcji w punkcie G. Widzimy zatem jak ważna jest historia danej próbki, jak ważne jest to jakiemu działaniu pola magnetycznego była poddawana. Mówiąc bardzo prosto interesuje nas w którym miejscu krzywej histerezy „znajduje” się nasza próbka.

Przenikalność magnetyczna

Kolejną ważną wielkością fizyczną z punku widzenia magnetyzmu jest przenikalność magnetyczna (ma ona ścisły związek z podatnością magnetyczną) i oznaczana jest literą
.

Przenikalność magnetyczna jest funkcją natężenia pola. I tak najpierw rośnie do pewnej wartości po czym maleje. Maksimum przenikalności magnetycznej przypada dla natężenia nieco mniejszego od natężenie, przy którym występuje nasycenie (J=const.)

W ferromagnetykach istnieje również ścisły związek między temperaturą a względną podatnością magnetyczną. Nosi on nazwę prawa Curie-Weissa i ma postać:

gdzie T_C - temperatura Curie

Po przekroczeniu temperatury Curie ferromagnetyk traci swoje właściwości ferromagnetyczne. Domeny rozpadają się, a momenty magnetyczne nie wykazują uporządkowania. Powyżej temperatury Curie nie można stosować prawa Curie-Weissa gdyż próbka przechodzi w paramagnetyk.

Antyferromagnetyki

Kolejnym ciekawym przykładem mogą być antyferromagnetyki. Zaliczamy do nich m.in. chrom, mangan. W ich wnętrzu momenty magnetyczne ustawiają się wzajemnie antyrównolegle.(to znaczy mają te same kierunki lecz przeciwne zwroty). W wyniku czego mają one skrajnie małą podatność magnetyczną i zachowują się jak słabe paramagnetyki. Dla antyferromagnetyków istnieje charakterystyczna temperatura zwana antyferromagnetycznym punktem Curie lub punktem Neela. Niektóre antyferromagnetyki takie jak dysproz, erb mają dwie takie temperatury. Poniżej dolnej temperatury wykazują właściwości ferromagnetyczne a powyżej górnej paramagnetyczne. Własności antyferromagnetyczne posiadają jedynie w granicach tych dwóch temperatur.

---