WSTĘP DO FIZYKI

Cześć 1

Prędkość, prędkość średnia, prędkość chwilowa.

Wzór na prędkość - postać podstawowa

				zapis skrócony:
Znaczenie symboli:
symbol	nazwa wielkości		rodowód symbolu	jednostka wielkości
v	prędkość		z ang. velocity - prędkość	m/s
S, ∆ S	droga		z ang. sector - odcinek	m
t, ∆ t	czas przebywania drogi S		z ang. time - czas	s
Przykład użycia definicji prędkości:
Jeżeli ciało przebyło drogę 15 m w ciągu 3 sekund, to średnia prędkość ciała wyniosła:
Wektorowa postać definicji prędkości
Ta postać wzoru mówi nam nie tylko o tym, że wartość prędkość (w m/s) otrzymujemy dzieląc drogę przez czas, ale jeszcze o tym, że kierunek wektora prędkości jest zgodny z kierunkiem przesuwania się ciała, czyli z wektorem S.
Wektor prędkości w ruchu prostoliniowym możemy rozumieć jako strzałkę, która łączy położenie początkowe z położeniem w jakim punkt znajdzie się po jednej sekundzie (jeśli prędkość się nie zmieni). Ten model rysunkowy jest słuszny, gdy skala położenia (1 metr) na rysunku jest taka sama jak skala prędkości (1m/s) .

Jednostki prędkości

Jednostką prędkości w układzie SI jest 1 "metr na sekundę"
Inne używane jednostki to np.: km/h (kilometr na godzinę) 1 cm/s 1 węzeł =  1 kn = 1 mila morska/godz.	1 km = 1000 m 1 cm = 0,01 m 1 mila morska = 1 852 m
	Przeliczenia jednostek:

Prędkość średnia, a prędkość chwilowa

Wzór w postaci jest właściwie wzorem na prędkość średnią. Oznacza to, że nie stawiamy sobie tu żadnych dodatkowych założeń dotyczących czasu ruchu i uwzględniamy jedynie początkowe i końcowe położenia ciała oraz czas przemieszczenia między tymi położeniami. Jeżeli więc ciało przez pół sekundy stało w miejscu, a przez następne pół przesunęło się na odległość 2 m to prędkość średnia w ciągu całej sekundy (na całych odcinku) wynosi 2m/s, mimo że tak naprawdę trochę ciało spoczywało, a później poruszało się znacznie szybciej niż średnia.

Mówiąc inaczej, prędkość średnia "nie wykrywa" nam szybkich zmian stanu ruchu ciała.

Definicja prędkości chwilowej Lepszym detektorem ruchu niż prędkość średnia jest prędkość chwilowa. Prędkość chwilowa jest to jakby prawie prędkość średnia, ale wyznaczana w ciągu bardzo krótkiego przedziału czasu (ściśle rzecz ujmując, powinniśmy wziąć przedział czasu nieskończenie bliski zera).

Prędkość chwilowa	postać różniczkowa	postać z użyciem granicy
postać skalarna
postać wektorowa

Jak przyrasta droga w ruchu jednostajnym?

Ruch jednostajny jest to taki ruch, w którym wartość prędkości jest stała. W ruchu jednostajnym droga co sekundę przyrasta o tę samą ilość metrów. Opisuje to wzór: S = v ∙t               - droga równa się prędkość razy czas gdzie: S - przebyta droga (w układzie SI w metrach m) v - prędkość ruchu (w układzie SI w m/s) t - czas ruchu (układzie SI w sekundach s)

 Ważne pojęcia związane z prędkością

Ruch jednostajnie opóźniony	Ruch w którym wartość prędkości maleje o tę samą wartość w jednostce czasu (przyspieszenie w tym ruchu jest stałe).
Ruch jednostajnie przyspieszony	Ruch w którym wartość prędkości rośnie o tę samą wartość w jednostce czasu (przyspieszenie w tym ruchu jest stałe).
Ruch jednostajny	ruch ze stałą wartością prędkości.
Ruch jednostajny prostoliniowy	ruch ze stałą wartością prędkości odbywający się po linii prostej.
Ruch jednostajny po okręgu	ruch którego torem jest okrąg, a wartość prędkości pozostaje stała. (wiadomości szukaj w rozdziale ruch po okręgu).
Ruch jednostajnie zmienny	Wspólna nazwa dla ruchu jednostajnie przyspieszonego i jednostajnie opóźnionego - jest to ruch w którym przyspieszenie ma stałą wartość.
Ruch niejednostajnie zmienny	ruch w którym przyspieszenie zmienia swoją wartość.
Ruch krzywoliniowy	ruch odbywający się po torze innym niż prosta albo odcinek tej prostej (przykład - ruch po okręgu).
Ruch zmienny	(jednostajnie zmienny, niejednostajnie zmienny) - ruch w którym prędkość zmienia swoją wartość
Tor	Krzywa którą zakreśla w przestrzeni (lub na płaszczyźnie) poruszający się punkt materialny.

 

Przyspieszenie

Definicja przyspieszenia

Wzór opisowy	Wzór symbolicznie

Znaczenie symboli:

symbol	nazwa wielkości	rodowód symbolu	jednostka wielkości
a	przyspieszenie	z ang. acceleration - przyspieszenie	m/s^2
vp	prędkość początkowa	ang. velocity - prędkość	m/s
vk	prędkość końcowa	jw.	m/s
t, ∆ t	czas (z ang. time), w jakim prędkość zmieniła się od vp do vk	z ang. time - czas	s
∆ v	różnica prędkości końcowej i początkowej ∆ v = vk - vp	∆ symbol delta (litera alfabetu greckiego) oznacza zazwyczaj przyrost jakiejś wielkości	m/s

Jednostka przyspieszenia Jednostką przyspieszenia jest "metr na sekundę kwadrat"

Przykład użycia definicji przyspieszenia: Przykład 1. Jeżeli prędkość ciała wzrosła od prędkości 1m/s do prędkość 7m/s w ciągu 2 sekund, to średnie przyspieszenie ciała wyniosło:

Zapamiętaj: Jeżeli przyspieszenie ciała jest stałe, to ruch nazywamy jednostajnie zmiennym Podział ruchów jednostajnie zmiennych
ruch jednostajnie przyspieszony	jeśli prędkość ciała rośnie zawsze o tyle samo w ciągu 1 sekundy
ruch jednostajnie opóźniony	jeśli  prędkość ciała maleje zawsze o tyle samo w ciągu 1 sekundy

Wzór na prędkość końcową w ruchu jednostajnie zmiennym  Poniżej podany jest wzór na prędkość końcową w ruchu jednostajnie zmiennym . Warto go zapamiętać, a przynajmniej przemyśleć, żeby w przyszłości można było go łatwo odtworzyć:   vk  =  vp + a∙ t

Znaki prędkości i przyspieszenia w ruchu przyspieszonym i opóźnionym

Jak to wyżej napisano, wzór na prędkość końcową w ruchu jednostajnie zmiennym ma postać: vk  =  vp + a∙ t    Powstaje pytanie: po czym poznać, czy konkretny wzór opisuje ruch jednostajnie przyspieszony, czy jednostajnie opóźniony? Oczywiście wzór w postaci ogólnej może pasować zarówno do jednego jak i drugiego przypadku. Przyjrzyjmy się więc liczbowym zastosowaniom wzoru - np.: vk = 4 m/s + 6 m/s^2 ∙ t vk = -15 m/s + 3 m/s^2 ∙ t vk = -5 m/s - 6 m/s^2 ∙ t vk = 5 m/s - 2 m/s^2 ∙ t Która z tych wzorów są wzorami na ruch przyspieszony, a które na opóźniony

Zasadą ogólną jest: Ruch przyspieszony mamy wtedy, gdy znak przyspieszenia jest taki sam jak znak prędkości. Ruch opóźniony mamy wtedy, gdy znak przyspieszenia jest przeciwny niż znak prędkości. Zatem ruch jest przyspieszony gdy: prędkość jest dodatnia i przyspieszenie jest dodatnie prędkość jest ujemna i przyspieszenie jest ujemne Zatem ruch jest opóźniony gdy: prędkość jest dodatnia i przyspieszenie jest ujemne prędkość jest ujemna i przyspieszenie jest dodatnie

Mamy więc już rozwiązanie naszych czterech przykładów problemowych:
vk = 4 m/s + 6 m/s^2 ∙ t	prędkość: v = + 4 m/s przyspieszenie:  + 6 m/s^2 Znaki obu wielkości są takie same, zatem ruch jest jednostajnie przyspieszony
vk = -15 m/s + 3 m/s^2 ∙ t	prędkość: v = - 15 m/s przyspieszenie:  + 3 m/s^2 Znaki obu wielkości są przeciwne, zatem ruch jest jednostajnie opóźniony
vk = -5 m/s - 6 m/s^2 ∙ t	prędkość: v = - 5 m/s przyspieszenie:  - 6 m/s^2 Znaki obu wielkości są takie same, zatem ruch jest jednostajnie przyspieszony
vk = 5 m/s - 2 m/s^2 ∙ t	prędkość: v = + 5 m/s przyspieszenie:  - 2 m/s^2 Znaki obu wielkości są przeciwne, zatem ruch jest jednostajnie opóźniony

Wektor przyspieszenia Wektor przyspieszenia możemy wyobrażać sobie jako strzałkę, która pokazuje o ile i w którą stronę wydłuży się (ale także skróci, lub skręci się) wektor prędkości po jednej sekundzie.

Ten model rysunkowy jest słuszny, gdy skala prędkości 1 m/s na rysunku jest taka sama jak skala przyspieszenia 1m/s^2.

W zależności od kierunku i zwrotu wektora przyspieszenia w stosunku do wektora prędkości możemy wyróżnić trzy sytuacje:

Gdy	wtedy	i mamy
wektor przyspieszenia jest skierowany zgodnie ze zwrotem prędkości	prędkość rośnie	ruch przyspieszony
wektor przyspieszenia jest skierowany przeciwnie do zwrotu prędkości	prędkość maleje	ruch opóźniony
wektor przyspieszenia jest skierowany pod kątem do wektora prędkości	prędkość będzie skręcać (zmienia się kierunek ruchu)	ruch krzywoliniowy

Możliwe są oczywiście przypadki mieszane - np. ruch krzywoliniowy przyspieszony, lub krzywoliniowy opóźniony; poza tym ruch może się zmieniać z przyspieszonego na opóźniony itp.

Postać wektorowa definicji przyspieszenia Do opisu ruchu krzywoliniowego niezbędne jest rozpatrywanie przyspieszenia jako wektora. Powyższa postać definicji przyspieszenia informuje nas o tym, że kierunek i zwrot przyspieszenia są zgodne z kierunkiem i zwrotem wektora zmiany prędkości.

Definicja przyspieszenia chwilowego Wzory i opisują tzw. przyspieszenie średnie, czyli przyspieszenie liczone dla dowolnych, nawet bardzo dużych przedziałów czasu. Jednak podając przyspieszenie najczęściej myślimy o jednej chwili ruchu. Dlatego "prawdziwe" przyspieszenie to tzw. przyspieszenie chwilowe, czyli przyspieszenie liczone dla bardzo małych (właściwie nieskończenie małych) odcinków drogi (lub nieskończenie małych przedziałów czasu). Matematycznie zapisuje się to albo z użyciem pojęcia granicy (limes - łac. granica), albo za pomocą - równoważnej - notacji różniczkowej.
Przyspieszenie chwilowe	postać różniczkowa	postać z użyciem granicy
postać skalarna
postać wektorowa

Składowa styczna i normalna przyspieszenia.

Przyspieszenie punktu jest równe geometrycznej sumie dwóch wektorów, z których jeden ma kierunek normalnej głównej - przyspieszenie normalne  an punktu, drugi ma kierunek stycznej przyspieszenie styczne  at (rys.16.6).

    Skalarne wyrażenia przyspieszenia normalnego 
  i  przyspieszenia stycznego 
  są rzutami przyspieszenia punktu na normalną główną i na  styczną w punkcie M1.
Rzut przyspieszenia na binormalną jest zerem.
Składowa normalna  an przyspieszenia jest skierowana do Środka krzywizny toru i równa modułowi jego rzutu na normalną główną.
Składowa styczna przyspieszenia  at może być dodatnia lub ujemna. Jeżeli przyspieszenie at jest zgodne z t, to rzut jego jest dodatni, jeżeli  at ma zwrot przeciwny do t, to rzut jego jest ujemny. Składowa styczna przyspieszenia, czyli at= dv/dt,  może być dodatnia lub ujemna w w zależności od tego , czy wartość liczbowa prędkości punktu jest rosnącą czy też malejącą funkcją czasu. Gdy v rośnie, wówczas  at > 0,  co oznacza, że przyspieszenie styczne ma w danej chwili ten sam kierunek co prędkość v. Gdy v maleje, wówczas przyspieszenie styczne ma kierunek przeciwny do  do kierunku prędkości punktu.
    Wreszcie, gdy  v = const, czyli gdy punkt porusza się ze stałą co do wartości prędkością, a więc ruchem jednostajnym, przyspieszenie styczne jest równe zeru.
Jeżeli znamy tor i jego krzywiznę w dowolnym punkcie oraz równanie ruchu  s = f(t), to możemy znaleźć rzuty przyspieszenia  na odpowiednie osie i obliczyć wartość i kierunek przyspieszenia punktu.
Wartość przyspieszenia: 

Kierunek przyspieszenia:

Mając zadany ruch punktu M równaniami skończonymi możemy obliczyć 
oraz

, a potem promień krzywizny

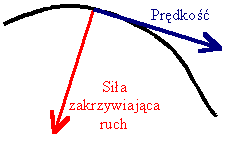
Przyspieszenie dośrodkowe Ciało na które nie działa żadna siła pozostaje w spoczynku, lub porusza się ruchem jednostajnym prostoliniowym. Jeżeli siła działa w kierunku ruchu, to nie będzie ona zakrzywiać toru - ruch będzie cały czas prostoliniowy (opóźniony, lub przyspieszony)    W przypadku jednak gdy siła działa pod kątem do kierunku ruchu (lub inaczej mówiąc ma jakąś składową prostopadłą do prędkości) to ruch będzie się zakrzywiał.   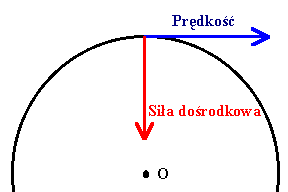Pomiędzy promieniem krzywizny tego zakrzywienia, prędkością ruchu i zakrzywiającym przyspieszeniem zachodzi związek (wzór na przyspieszenie dośrodkowe):     Powyższy wzór najprościej jest odnieść do ruchu jednostajnego po okręgu. W tym przypadku promień krzywizny jest po prostu promieniem okręgu, a środek krzywizny jest o prostu środkiem okręgu. Dla ruchów o torach bardziej skomplikowanych promień krzywizny będzie zmieniał w trakcie ruchu i jest określony tylko dla każdego punktu osobno.

Dla ruchu po okręgu:	Dla dowolnych ruchów krzywoliniowych:
Znaczenie symboli: v - prędkość ruchu po okręgu (w układzie SI w m/s) R - promień okręgu (w układzie SI w m) adośr - przyspieszenie dośrodkowe zakrzywiające tor ruchu (w układzie SI w m/s^2)	Znaczenie symboli: v - prędkość ruchu w danym momencie (w układzie SI w m/s) R - promień krzywizny toru (w układzie SI w m) adośr - przyspieszenie dośrodkowe zakrzywiające tor ruchu, lub inaczej przyspieszenie normalne w tym ruchu (w układzie SI w m/s^2)

Jeżeli w miejsce prędkości liniowej podstawimy v = ω·R to otrzymamy drugi wzór na wartość przyspieszenia dośrodkowego: adośr = ω^2 ∙ R Siła dośrodkowa Z przyspieszeniem dośrodkowym możemy oczywiście związać siłę dośrodkową. W tym celu trzeba wartość przyspieszenia podstawić do wzoru na siłę wynikającego z II zasady dynamiki (F = m ∙a), czyli: Fdosr = m ∙adosr   Stąd:   lub: Fdosr = m ∙ω ^2 ∙ R

Ruch jednostajny prostoliniowy

Ruch jednostajny prostoliniowy to taki, w którym prędkość ma stałą wartość . Punkt materialny poruszający się po torze prostoliniowym przebywa jednakowe odcinki drogi  w jednakowych odstępach czasu . Prędkość średnia w tym ruchu równa jest prędkości chwilowej. Przy założeniu, że  i  oraz że  wartość prędkości wyraża się jako . Z przekształcenia tego otrzymuje się wzór na drogę, równy: . Symbole  są wartościami końcowymi, a  wartościami mierzonymi na początku trwania ruchu.

 

Transformacja Galileusza

Omawiając zasady dynamiki Newtona stwierdziliśmy, że prawa przyrody (w szczególności fizyki) są takie same bez względu na to, czy obserwujemy je z układu nie poruszającego się, czy z ruchomego, ale poruszającego się bez przyśpieszenia (układy inercjalne).

Spróbujemy teraz opisać zjawiska widziane z dwóch różnych inercjalnych układów odniesienia, poruszających się względem siebie (rysunek). W tym celu wyobraźmy sobie, obserwatora na ziemi, który rejestruje dwa wybuchy na pewnej, jednakowej wysokości. Odległość między miejscami wybuchów wynosi, (według ziemskiego obserwatora) Δx, natomiast czas między wybuchami Δt. Te same dwa zdarzenia obserwowane są przez pasażera samolotu lecącego z prędkością V po linii prostej łączącej miejsca wybuchów. Względem lokalnego układu odniesienia związanego z lecącym samolotem różnica położeń wybuchów wynosi Δx', a różnica czasu Δt'.

Porównajmy teraz spostrzeżenia obserwatorów na ziemi i w samolocie. Zróbmy to np. z pozycji obserwatora na ziemi, który próbuje opisać to co widzą pasażerowie samolotu.

Jeżeli, pierwszy wybuch nastąpił w punkcie x₁' (względem samolotu), a drugi po czasie Δt, to w tym czasie samolot przeleciał drogę VΔt (względem obserwatora na Ziemi) i drugi wybuch został zaobserwowany w punkcie

czyli

Jednocześnie, ponieważ samolot leci wzdłuż linii łączącej wybuchy, to Δy' = Δz' = 0. Oczywistym wydaje się też, że Δt' = Δt.

Otrzymaliśmy więc wzory przekładające wyniki obserwacji jednego obserwatora na spostrzeżenia drugiego

(11.1)

Te równania noszą nazwę transformacji Galileusza

Sprawdźmy, czy stosując powyższe wzory do opisu doświadczeń, otrzymamy takie same wyniki, niezależnie od układu w którym to doświadczenie opisujemy. Jako przykład wybierzmy ciało poruszające wzdłuż osi x ruchem jednostajnie przyspieszonym z przyspieszeniem a. W układzie nieruchomym prędkość chwilowa ciała wynosi

Jego przyspieszenie jest stałe i równe a. Natomiast obserwator w pojeździe poruszającym się wzdłuż osi x ze stałą prędkością V rejestruje, że w czasie Δt' ciało przebywa odległość Δx'. Zatem prędkość chwilowa ciała zmierzonego przez tego obserwatora wynosi

Zgodnie z transformacją Galileusza Δx' = Δx − VΔt, oraz Δt' = Δt, więc

Otrzymaliśmy prędkość względną jednego obiektu względem drugiego co jest wynikiem intuicyjnie oczywistym. Natomiast przyśpieszenie w układzie poruszającym się wynosi

Widać, że w tym przypadku zastosowanie wzorów transformacji Galileusza daje wynik zgodny z doświadczeniem. Jednak nie jest to prawdą w każdym przypadku. Miedzy innymi stwierdzono, że ta transformacja zastosowana do równań Maxwella nie daje tych samych wyników dla omawianych układów inercjalnych. W szczególności z praw Maxwella wynika, że prędkość światła jest podstawową stałą przyrody i powinna być taka sama w każdym układzie odniesienia.

Oznacza to na przykład, że gdy impuls światła rozchodzący się w próżni w kierunku x jest obserwowany przez dwóch obserwatorów (patrz na tekst i rysunek powyżej) to zarówno obserwator nieruchomy jak poruszający się z prędkością V (względem pierwszego) zmierzą identyczną prędkość impulsu c = 2.998⋅10⁸ m/s. Tymczasem zgodnie z transformacją Galileusza i ze zdrowym rozsądkiem powinniśmy otrzymać wartość
c - V. Wykonano szereg doświadczeń, w których próbowano podważyć równania Maxwella, a w szczególności próbowano pokazać, że prędkość światła, tak jak prędkość dźwięku zależy od układu odniesienia (stosuje się do transformacji Galileusza). Najsławniejsze z nich, to doświadczenie Michelsona-Morleya mające na celu wykrycie wpływu ruchu orbitalnego Ziemi na prędkość światła poprzez pomiar prędkości światła w kierunku prostopadłym i równoległym do ruchu Ziemi. Wszystkie te doświadczenia dały wynik negatywny i musimy uznać, że prędkość światła w próżni jest jednakowa we wszystkich inercjalnych układach odniesienia.

Prędkość światła c = 2.988⋅10⁸ m/s we wszystkich układach odniesienia.

Rozpatrzmy teraz niektóre wnioski wynikające ze sta*ości prędkości świat*a.

Ruch jednostajnie przyspieszony

Ruch prostoliniowy jednostajnie przyspieszony to taki, w którym punkt materialny porusza się ze stałym przyspieszeniem.    Przyrost prędkości wyraża się jako
, przy czym
 jest prędkością punktu materialnego w początkowej chwili
, natomiast
 oznacza prędkość końcową, w końcowej chwili
. Przyjmując za
, okres czasu
 jest identyczny jak
. Uzyskuje się postać:
. Po przekształceniu otrzymuje się pierwsze równanie ruchu prostoliniowego jednostajnie przyspieszonego:
. Droga, jaka przebywa ciało poruszające się ruchem jednostajnie przyspieszonym w chwili czasu
, jest równa średniej arytmetycznej sumy prędkości początkowej i końcowej, pomnożonej przez czas
. Zapisujemy to wzorem
. Po wstawieniu pierwszego równania ruchu, otrzymuje się równanie
, które jest drugim równaniem ruchu jednostajnie przyspieszonego. Zależność tę można otrzymać też wyprowadzić korzystając z rachunku całkowego:

.

 

Rzut ukośny

Rzut ukośny Opis ruchu W rzucie ukośnym mamy do czynienia z lotem ciała wyrzuconego z poziomu zerowego (y0 = 0). Ciału jest nadawana prędkość o wartości v0, skierowana pod kątem α do poziomu. Ciało porusza się łukiem, by po pewnym czasie opaść na ziemię. Wygodnie jest umieścić rysunek rzutu ukośnego w układzie współrzędnych, co ułatwia orientację w nazwach zmiennych i pozwala na wyprowadzenie równania toru. Odległość jaką przebywa ciało w poziomie do momentu upadku na poziom początkowy nazwiemy zasięgiem (Z) rzutu ukośnego.
Początkowe położenie:	x = 0 y = 0
Kąt, jaki prędkość początkowa tworzy z poziomem:	α
Prędkość początkowa ma wartość v0	Prędkość pocz. pozioma: v0x = v0 · cos α Prędkość pocz. pionowa: v0y = v0 · sin α
Przyspieszenie  ma wartość g.	Przyspieszenie w tym ruchu jest stałe i jest skierowane pionowo w dół.
W przypadku gdy nie musimy uwzględniać oporu powietrza, torem ruchu ciała jest parabola. Ruch ciała rozkłada się wtedy na dwa ruchy prostsze: ruch w poziomie (współrzędna X-owa) - odbywa się ze stałą prędkością o wartości składowej poziomej prędkości początkowej v0X ruch w pionie (współrzędna Y-owa) - jest w istocie rzutem pionowym, czyli ruchem jednostajnie zmiennym z prędkością początkową równą składowej pionowej v0Y. Wzory opisujące rzut ukośny Prędkość pozioma vx (w dowolnej chwili czasu t): vx = v0x = const vx = v0·cos α Prędkość pionowa vy po czasie t: vy = v0·sin α - g·t   Odległość pozioma przebyta w poziomie po czasie t: x = vox ·t = v0·t·cos α Wysokość na jakiej znajduje się ciało po czasie t: Czas lotu do momentu upadku na poziom początkowy:   Czas wznoszenia do osiągnięcia maksymalnej wysokości: tw = ½ ts
Zasięg rzutu poziomego (odległość przebyta w poziomie do momentu upadku na poziom początkowy):
Maksymalna osiągnięta wysokość:
Równanie toru rzutu ukośnego
Tor rzutu ukośnego ma kształt paraboli skierowanej ramionami w dół

Ruch obrotowy

Wstęp Ruch po okręgu jest przykładem ruchu zachodzącego w dwóch wymiarach. Jest on zazwyczaj znacznie bardziej skomplikowany od ruchu prostoliniowego. Gdyby chcieć dokładnie opisywać położenie punktu poruszającego się po okręgu posługując się kartezjańskim układem XY, wtedy trzeba użyć funkcji trygonometrycznych sinus i kosinus. Funkcje te są dość skomplikowane w użyciu i niewygodne, dlatego rzadko stosuje się te współrzędne do opisu ruchów obrotowych. Kąt w radianach - definicja Ponieważ tor poruszającego się punktu jest całkowicie wyznaczony kształtem okręgu, można tak zmienić sposób opisu, że będzie on prostszy. Dodatkową zaletą opisu w układzie biegunowym, jest fakt, że dla całkowitego przekazania informacji o położeniu wystarczy tylko jedna zmienna (plus najczęściej stały promień okręgu R).
Tą dobrą zmienną może być nią np. długość drogi przebytej wzdłuż okręgu  ∆L, lub (co się częściej stosuje) - kąt obrotu α  (lub ∆α).	Znaczenie symboli:  ∆α, α - kąt (w układzie SI w radianach, co jest równoważne wielkości niemianowanej) ∆L - długość drogi przebytej wzdłuż łuku okręgu (w układzie SI w metrach m) R - promień okręgu którego fragmentem jest zakreślany łuk (w układzie SI w metrach m).
Powyższy wzór może być uznany za definicję kąta wyrażonego w radianach. Dlatego warto go zapamiętać.

Prędkość kątowa
Podczas ruchu wraz z przebywaną drogą ∆L, zmienia się ∆α, dlatego celowe jest wprowadzenie wielkości charakteryzującej szybkość zmiany kąta. Wielkością tego rodzaju jest tzw. prędkość kątowa. Oznaczamy ją ω (mała grecka litera omega):
	Znaczenie symboli: ω - prędkość kątowa (w rad/s, lub opuszczając radiany 1/s = s^-1)  ∆α - kąt zakreślony przez promień wodzący (w radianach) ∆t - czas w jakim odbywa się ruch, lub jego fragment (w sekundach s)
Jak widać z tego wzoru: Prędkość kątowa jest równa kątowi zakreślonemu podczas ruchu podzielonemu przez czas.
Pomiędzy prędkością liniową punktu poruszającego się po okręgu, a prędkością kątową istnieje prosta zależność: Znaczenie symboli: ω  - prędkość kątowa (w rad/s, lub opuszczając radiany 1/s = s^-1) R - promień okręgu którego fragmentem jest zakreślany łuk (najczęściej w metrach m). v - prędkość liniowa, czyli „zwykła” prędkość punktu (najczęściej w m/s)	Wyprowadzenie zależności z lewej strony: 1. Do wzoru na prędkość kątową podstawiamy definicję kąta:   2. uwzględniamy że prędkość liniowa to:   3. więc ostatecznie:
Zwróćmy uwagę na lekka zmianę nazewnictwa:   jest nazywana prędkością liniową punktu poruszającego się po okręgu (choć jest przecież po prostu zwykłą prędkością). Ten dodatek "liniowa" jest używany wtedy gdy omawiamy ruch po okręgu - gdy wielkość tę trzeba dokładniej odróżniać od prędkości kątowej.

Ruch jednostajny po okręgu
Jeżeli prędkość kątowa punktu poruszającego się po okręgu nie zmienia się, to ruch nazywamy ruchem jednostajnym po okręgu.   Przykładem ruchu jednostajnego po okręgu może być ruch poproszka leżącego na obracającej się płycie gramofonowej, lub ruch obiektu leżącego na powierzchni obserwowany z bieguna ziemskiego w układzie nie obracającym się wraz z Ziemią (np. wtedy, gdy jedna oś układu odniesienia cały czas jest zwrócona na Słońce lub odległą gwiazdę).	w ruchu jednostajnym po okręgu ω  = const
W ruchu jednostajnym po okręgu przyspieszenie (jako wektor) nie jest równe zero, mimo że wartość prędkości nie zmienia się. Z dwóch składowych przyspieszenia: stycznej i normalnej tylko jedna ma wartość zero. składowa styczna (zmieniająca wartość prędkości) ma wartość zero składowa normalna (zmieniająca kierunek prędkości) jest niezerowa Jest tak, ponieważ kierunek prędkości ulega ciągłej zmianie - prędkość musi być ciągle zakrzywiana do środka okręgu. Dlatego z ruchem jednostajnym po okręgu związana jest stała wartość przyspieszenia nazywanego przyspieszeniem dośrodkowym.
Przyspieszenie dośrodkowe Wartość przyspieszenia dośrodkowego wyliczamy ze wzoru:    Istnieje też postać powyższego wzoru uzależniająca przyspieszenie dośrodkowe od prędkości kątowej ω.  Jeżeli w miejsce prędkości liniowej podstawimy v = ω·R (jest to proste wyliczenie v ze wzoru    podanego wyżej ) to otrzymamy: adośr = ω^2·R  Z powyższego wzoru widać wyraźnie, że dwukrotne zwiększenie prędkości obrotu zaowocuje aż czterokrotnym zwiększeniem przyspieszenia dośrodkowego.

Kilka uwag terminologicznych związanych z czasem w ruchu po okręgu Okres ruchu po okręgu

Okres ruchu po okręgu (T) jest to czas, po którym punkt materialny wykona jeden pełny obieg całego okręgu. Jednostką okresu jest sekunda (minuta, godzina...) [T] = s Jeżeli punkt materialny wykonuje N obiegów okręgu w ciągu czasu t, wtedy oczywiście okres dany jest wzorem:   Znaczenie symboli: T - okres ruchu (w sekundach s) N - ilość wykonanych (również niepełnych, wtedy będzie ułamek) okrążeń okręgu (liczba niemianowana) t - czas w jakim odbywa się ruch, lub jego fragment (w sekundach s)

Częstotliwość ruchu obrotowego i ruchu po okręgu Częstotliwość (f) jest to ilość obiegów okręgu wykonanych w jednostce czasu. Jednostką częstotliwości jest jeden herc [f] = Hz = 1/s Jeżeli punkt materialny wykonuje N obiegów okręgu w ciągu czasu t, to częstotliwość wyliczymy ze wzoru:   Znaczenie symboli: f - częstotliwość (w Hz = 1/s = s^-1) N - ilość wykonanych (również niepełnych - wtedy pojawi się ułamek) okrążeń okręgu (liczba niemianowana) t - czas w jakim odbywa się ruch, lub jego fragment (w sekundach s)

Z porównania obu tych definicji wynika, że:   Użyteczne też mogą być wzory wyrażające prędkość kątową w ruchu po okręgu za pomocą częstotliwości, lub okresu: ω = 2 π f

Zasady dynamiki Newtona, pęd, popęd

Wzór na pęd Pęd definiujemy jako iloczyn masy i prędkości ciała. Pęd jest wielkością wektorową. Jednostka pędu Jednostką pędu w układzie SI jest: kilogram razy metr na sekundę. [p] = kg • m/s

Dlaczego pęd jest tak ważną wielkością? Różne wielkości fizyczne (np. masy, prędkości, przyspieszenia, odległości) można  przez siebie mnożyć, dzielić, dodawać i odejmować w rozmaitych kombinacjach, ale tylko nieliczne otrzymane w ten sposób wzory dają użyteczne wielkości. Bo tylko wtedy, gdy wielkość w jakiejś szczególnej klasie sytuacji jest stała staje się on użyteczna fizykowi. Tak jest w przypadku masy - większość ciał ma stałą masę (o ile np. ich nie podzielimy na kawałki); podobnie też np. gęstość jest niezmienna dopóki nie zmienimy istotnie warunków w jakich znajduje się substancja. Gdyby zaś ta sama gęstość, bez żadnego powodu była raz większa, raz mniejsza, to wielkość owa nic by nam o substancjach nie mówiła. Dlatego też w zasadzie wszystkie "ważne" wielkości fizyczne zachowują w określonych warunkach stałą wartość, mimo zmiany wielkości je tworzących. I tak też jest w przypadku pędu - obowiązuje:

ZASADA ZACHOWANIA PĘDU

Jeżeli na jakiś układ ciał nie działają siły z zewnątrz, wtedy układ ten ma stały pęd.

Czyli: jeżeli F = 0, to p = const Inaczej mówiąc: Zmienić pęd układu może tylko siła działająca z zewnątrz układu. Zasada zachowania pędu jest innym sformułowaniem pierwszej zasady dynamiki Newtona, jako że omawiany przypadek braku siły zewnętrznej rozpatrywany jest w układzie inercjalnym. O tym czym są siły więcej można się dowiedzieć z rozdziału siła .

Prosty przykład zastosowania pojęcia pędu: Jeżeli, stojąc sobie na bardzo śliskim lodzie i odepchniemy od siebie stojące też na tym lodzie sanki, to uzyskają one pęd w jedna stronę, ale my z kolei też zaczniemy ślizgać się po lodzie w kierunku przeciwnym. W układzie My - Sanki obowiązuje zasada akcji i reakcji - my odpychamy sanki, ale sami też odpychamy się od sanek. Pęd niesiony przez odepchnięte sanki jest równoważony przez pęd odpychającego skierowany przeciwnie - w sumie pęd całego układu nie zmienia się. Pęd niesiony przez sanki (w prawo) jest równy co do wartości pędowi odbieranemu przez człowieka (w lewo). Powiedzieliśmy tu o kierunku (choć właściwie myśleliśmy o "zwrocie") pędu. Bo: pęd, jako wielkość wektorowa, ma zwrot, kierunek i wartość. Wynika stąd też, że zasadę zachowania pędu powinniśmy raczej zapisać wzorem że strzałkami nad wektorami pędu i siły:

Związek między siłą i pędem, popęd siły Z tego, że tylko brak siły owocuje stałością pędu, wynika nowy wniosek: Siła zmienia pęd ciała Wszystko odbywa się według wzoru: (gdzie: ∆p jest zmianą pędu, F jest siłą, a ∆t - czasem działania tej siły) Co można zinterpretować słownie jako: Zmiana pędu równa jest iloczynowi siły i czasu jej działania Wielkość po prawej stronie wzoru (iloczyn siły i czasu) nazywana jest często popędem siły. Co daje nam możliwość przeczytania tego wzoru w jeszcze jeden sposób: Zmiana pędu jest równa popędowi siły ją wywołującemu. Wzór w przekształconej postaci może posłużyć jako definicja siły (patrz też rozdział siła):
	Siła jest równa szybkości zmiany pędu
Ten ostatni wzór na siłę jest bardziej użyteczny w naukowych zastosowaniach niż, najczęściej używana w szkole, postać z przyspieszeniem.

statek zderza się z krą lodową i grzęźnie w niej - pęd statku i kry po zderzeniu jest taki sam jak pęd statku przed zderzeniem

kula uderza w deskę i przebija ją na wylot, zmniejszając przy tym swoją prędkość - kula oddaje część swojego pędu desce.

jedna kula bilardowa uderza w drugą - kula uderzająca przekazuje część (lub całość) pędu drugiej kuli.

bramkarz łapie lecącą piłkę - wraz z piłką dostaje także jej pęd.

i inne - np. biegnący człowiek wskakuje do wózka lub łódki...

Przykłady zadań i problemów, do rozwiązania których używamy pojęcia pędu.
	Czy tak dynamiczny rozwój nauki w naszych czasach nie oznacza, że świat stanął na zakręcie?
We wszystkich tych przypadkach do opisania tego co dzieje się tuż po zderzeniu stosujemy zasadę zachowania pędu. Tę samą zasadę stosujemy też do zjawisk będących odwrotnością zderzenia - opierających się na zasadzie odrzutu. Np. chłopiec stojący na łódce wyrzuca ciężki pakunek. Jak szybko będzie poruszać się łódka? - pęd chłopca z łódką równoważy pęd wyrzuconego pakunku. granat rozrywa się dwie części - jedna część uzyskuje pęd w jedną stronę, a druga, taki sam pęd w stronę przeciwną rakieta wyrzuca gazy odrzutowe w kierunku przeciwnym do ruchu. Sama więc uzyskuje pęd odwrotny do pędu gazów. działo wystrzeliwuje pocisk - znów występuje wtedy zjawisko odrzutu powodujące, że działo cofa się w kierunku przeciwnym do ruchu pocisku.

Rozwiązanie zadania z użyciem pędu A oto przykład rozwiązania zadania w oparciu o zasadę zachowania pędu:

Zadanie: Do łódki o masie 30 kg wskakuje chłopiec o masie 60 kg biegnący z prędkością 6m/s. Jaką prędkość uzyska łódka tuż po wskoczeniu chłopca?

Rozwiązanie: Ponieważ mamy do czynienia że "zderzeniem" łódki i chłopca, więc zastosujemy zasadę zachowania pędu. Dla potrzeb tego problemu sformułujmy ją tak: Suma pędu chłopca i łódki przed zderzeniem jest równa sumie pędów tych obiektów po zderzeniu. Pęd całkowity przed i po zderzeniu jest taki sam, jednak inaczej się rozkłada - przed zderzeniem całość pędu niósł że sobą chłopiec, pęd łódki był zero. Po zderzeniu łódka i chłopiec poruszają się razem z jedną prędkością dzieląc się pędem do spółki. Weźmy się zatem za obliczenia:

Pęd (wektorowo) wyraża się wzorem:
zastosowanie wektorów wielowymiarowych w tym zadaniu nie jest potrzebne ponieważ cała treść zadania da się opisać jednymi kierunkiem poziomym. Dlatego możemy spokojnie pominąć znaki wektorów nad symbolami.	p = m ∙ V

Musimy powiązać ze sobą pędy przed i po zderzeniu.

pęd przed zderzeniem		pęd po zderzeniu
pęd chłopca	pęd łódki = 0	pęd chłopca i łódki razem
pchł = m chł ∙ V chł	pł = mł ∙ 0	pchł+ł = (m chł + mł) ∙ V końcowe

Z zasady zachowania pędu mamy: pcałkowity_przed zderzeniem = pcałkowity_po zderzeniu

Czyli	pchł_przed zderzeniem + pł_przed zderzeniem = pchł+ł_po zderzeniu
Zatem	m chł ∙ V chł + 0 = (m chł +mł) ∙ V końcowe
Po podzieleniu obu stron równania przez nawias z prawej strony i zamianie stron równania otrzymamy wzór końcowy:
Stąd można wyliczyć wartość prędkości:
Jak widać, łódka przyhamowała nieco ruch chłopca, bo jego prędkość zmalała. Jednocześnie chłopiec rozpędził (poruszył) łódkę. Powyższą sytuację, w której jedno rozpędzone ciało łączy się z drugim, a później oba ciała poruszają się razem nasi nazwę zderzenia niesprężystego.

Układy odniesienia i I zasada dynamiki Wstęp I zasada dynamiki Newtona nie została, wbrew nazwie, odkryta przez sir Izaaka Newtona (Newton żył w Anglii w latach 1643 - 1727; był matematykiem i fizykiem). Zasadę tę zawdzięczamy, żyjącemu przed nim, fizykowi włoskiemu Galileo Galilei (1564-1642), zwanemu Galileuszem. Newton zasadę powyższą powiązał w całość z innymi podstawowymi prawami mechaniki klasycznej i nadał jej bardziej sformalizowaną postać.
Układ inercjalny Ze wszystkich układów odniesienia najbardziej podstawowym dla fizyki jest układ inercjalny (określanego też jako układ „inercyjny”). Układ ten posiada pewną szczególną własność. Otóż dla ciał obserwowanych z poziomu tego układu zachodzi: Gdy na ciało nie działają żadne siły zewnętrzne, lub działające siły równoważą się, wtedy ciało to pozostaje w spoczynku, lub porusza się ruchem jednostajnym prostoliniowym. Inaczej mówiąc, w układzie inercjalnym przyspieszenie pojawia się tylko jako rezultat działania (niezrównoważonej) siły.   Z kolei gdy pojawi się siła zewnętrzna... I  Tylko w układzie inercjalnym powyższe wynikania są słuszne!
Bo z kolei w układach nieinercjalnych możemy mieć ruch przyspieszony jakiegoś ciała bez działania sił, lub ciało może być w spoczynku, choć działa na niego niezrównoważona siła. Osoby stykające się z problemem po raz pierwszy zadadzą sobie zapewne dość oczywiste pytanie: A kiedy to ciało miałoby się zacząć poruszać bez siły go popychającej? - a mogłoby! Wystarczy, że sam układ odniesienia jest w ruchu zmiennym (porusza się z przyspieszeniem). Wtedy „widzi on” całe otoczenie „skażone” swoim „osobistym” przyspieszeniem. Tak jest we wszystkich układach nieinercjalnych - ponieważ poruszają się one ruchem zmiennym względem układów inercjalnych to, w nich mamy ruch przyspieszony bez siły, lub spoczynek mimo, że siły działają.	Instrukcje nauczyciela do zachowania na maturze: - w czasie matury wolno jest mieć jedynie długopis i dokument potwierdzający tożsamość. Ewentualnie można mieć maskotkę i jakieś nie budzące podejrzeń drobiazgi. Kanapki zostaną wam rozdane. Gorące napoje też. Pytanie z sali:  - a jeśli ktoś pije tylko ziółka?  - można poprosić o zrobienie herbatki z dziurawca, ale w żadnym wypadku nikt nie dostanie herbatki z szałwi i mięty!!! - Dlaczego? - jak tak lubię szałwię... Przecież wszyscy wiedzą, że szałwia ma działanie ściągające!
Do czego służy pojęcie układu inercjalnego? Pojęcie układu inercjalnego ma jeden podstawowy cele (oprócz męczenia uczniów szkole nauką z nim związaną ;-))).). Układ inercjalny ustala punkt wyjścia do rozważań nad ruchem i przyczynami, dla których ten ruch zachodzi tak, a nie inaczej. Czyli dopiero do momentu "posiadania" układu inercjalnego będziemy w stanie wystartować z ustalaniem związku między siłą, a przyspieszeniem. Gdybyśmy nie mogli ustalić na początek tego, że z braku siły można wnioskować brak przyspieszenia, to bez sensu byłoby zastanawianie się nad tym, jaka siła powoduje jakie przyspieszenie (mogłoby być przecież dowolne). A wtedy nie moglibyśmy wprowadzić II zasady dynamiki, dzięki której powstała niemal cała mechanika klasyczna. Tak więc, aby cała logiczna maszyneria zadziałała, musimy zapostulować: Istnieją układy inercjalne. I od nich się wszystko zaczyna. W tych to układach będzie rozgrywała się większość zdarzeń z fizyki. W nich, bo dla układów inercjalnych opis zjawisk jest najłatwiejszy. I zasada dynamiki Ów fakt, że Istnieją układy inercjalne można potraktować jako jedną z wersji sformułowania I zasady dynamiki Newtona. Sam Newton ową zasadę zapisał w nieco innej, bardziej znanej, formie: Jeżeli na ciało nie działa żadna siła, lub działające siły równoważą się, wtedy ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. Ta oryginalna wersja I zasady dynamiki jest jednak trochę niedoskonała, bo przecież w pewnych warunkach tak sformułowane prawo nie obowiązuje. W szczególności odnosi się ono tylko do sytuacji zachodzących w układach nieinercjalnych. Dlatego precyzyjniejszym ujęciem tego prawa jest zdefiniowanie układu inercjalnego i zapostulowanie jego istnienia - tak jak to było omówione wyżej. W ten sposób nasza I zasada dynamiki spełnia swoje podstawowe zadanie - daje punkt wyjścia do wprowadzenia II, a potem także III zasady dynamiki Newtona.

W wersji zwanej uogólnioną (uogólniona druga zasada dynamiki), obowiązuje dla ciała o zmiennej masie w mechanice relatywistycznej:

Zmiana pędu ciała jest proporcjonalna do działającej siły wypadkowej.

Przy prędkościach, w których nie występują efekty relatywistyczne czyli dla ciała nie zmieniającego masy w wyniku zmian prędkości, zasadę tę można wyrazić w wersji uproszczonej (ta wersja funkcjonuje na wstępnych etapach nauczania fizyki)

Przyspieszenie z jakim porusza się ciało jest proporcjonalne do działającej siły i odwrotnie proporcjonalne do masy ciała. Kierunek i zwrot przyspieszenia jest zgodny z kierunkiem i zwrotem siły.

Sformułowanie oryginalne.

''Zmiana ruchu jest proporcjonalna do przyłożonej siły poruszającej i odbywa się w kierunku prostej, wzdłuż której siła jest przyłożona.''

III zasada dynamiki Jeżeli ciało A działa na ciało B siłą FAB, to ciało B działa na ciało A siłą FBA, o takim samym kierunku i wartości jak FAB, ale przeciwnym zwrocie.
Da się to zapisać wzorem:
Powyższe prawo nazywane jest niekiedy zasadą „akcji i reakcji” Uwaga: siły występujące w III zasadzie dynamiki nie równoważą się. Siła FAB, nie równoważy się z siłą FBA , ponieważ działają na różne ciała - siłą FAB działa na ciało B, a siła FBA na ciało A.

Przykład III zasady dynamiki Newtona - klocek leżący na poziomej powierzchni
Klocek spoczywający na poziomej powierzchni. Siła działająca ze strony powierzchni na leżący na niej klocek jest równa sile, jaką ten klocek działa na tę powierzchnię NP->K = - NK->P
Np. Jeżeli ciężar klocka wynosi 20 N, to jego nacisk na powierzchnię też wynosi 20N. Z kolei powierzchnia podtrzymuje klocek siłą o tej samej wartości 20N.

Popęd siły (impuls siły) - wektorowa wielkość fizyczna charakteryzująca działanie siły F na ciało w przeciągu czasu Dt; równa jest iloczynowi: F × Dt.

Moment bezwładności. Twierdzenie Steinera.

Momentem bezwładności

bryły sztywnej względem pewnej osi (definiuje się również inne momenty bezwładności) nazywamy wyrażenie

. Wzór ten odczytujemy następująco:
Aby znaleźć moment bezwładności ciała należy podzielić w myśli to ciało na fragmenty tak małe, aby każdy można było traktować jak punkt materialny o pewnej masie m_i, pomnożyć jego masę przez kwadrat jej odlęgłości od osi obrotu r_i² i wszystkie otrzymane iloczyny do siebie dodać. Ta dosyć skomplikowana recepta może być zastoswana praktycznie tylko do ciał, które składają się ze skończonej liczby niewielkich elementów, które można potraktować w przybliżeniu jak zbiór niezależnych punktów materialnych. W praktyce, do ciał rzeczywistych, a więc takich dla których masa jest rozłożona w sposób ciągły stosuje się postać całkową definicji pozwalającą obliczać rzeczywiste momenty bezwładności:

We wzorze tym r² oznacza zmienną określającą odległość elementu masy dm od osi obrotu.
W oparciu o tę zależność można stosunkowo prosto wyliczyć moment bezwładności kilku popularnych brył:

Wszystkie powyższe wzory określają moment bezwładności brył względem osi przechodzących przez środek masy danej bryły. Do określenia momentu bezwładności względem innej osi pomocne jest

Twierdzenie Steinera

Twierdzenie to mówi, że jeśli znamy moment bezwładności I_o danego ciała względem pewnej osi przechodzącej przez środek masy tego ciała,
to aby obliczyć moment bezwładności I względem dowolnej innej osi równoległej do niej,
należy do momentu I_o dodać iloczyn masy ciała i kwadratu odległości d między tymi osiami czyli md²:
Ilustruje to rysunek powyżej, na przykładzie którego możemy wyliczyć moment bezwładności kuli względem osi stycznej do kuli:

Moment siły

Moment M siły działającej na ciało to wielkość wektorowa określona przez iloczyn wektorowy działającej siły i promienia. Wektor momentu siły jest prostopadły do płaszczyzny wyznaczonej przez wektor siły i wektor r, a jego zwrot określa reguła śruby prawoskrętnej. Zgodnie z tą regułą, jeśli będziemy obracali po najkrótszej drodze pierwszy wektor (tu: r) tak, aby pokrył się z drugim (tu: F), to obracana w tym samym kierunku śruba prawoskrętna będzie przesuwać się (będzie wkręcana lub wykręcana) w kierunku określającym zwrot wektora M

II zasada dynamiki ruchu obrotowego:

Zasada zachowania momentu pędu

Ruch ciała o zmiennej masie

2

www.mort.friko.pl

---