Wyznaczanie stałej siatki dyfrakcyjnej
Światło jest falą elektromagnetyczną rozchodzącą się w próżni ze stałą prędkością c. Do celów optycznych potrzebne jest jedynie opisanie w czasie wektora elektrycznego fali świetlnej równaniem (dla fali biegnącej w kierunku osi x): 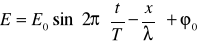
Zgodnie z zasadą Hyghensa, każdy punkt, który fala napotyka na swojej drodze staje się źródłem nowej fali kulistej; położenie fali można odczytać jako styczną do fal cząstkowych. Jest to podstawa wyjaśnienia zjawisk dyfrakcji i interferencji.
Interferencja jest to wzajemne nakładanie się fal. W określonym punkcie przestrzeni nastąpi wzmocnienie lub wygaszenie amplitudy w zależności od faz fal w tym punkcie. Fale będą się wygaszać wzajemnie gdy ich fazy będą przeciwne, natomiast będą się maksymalnie wzmacniać, gdy ich fazy będą zgodne.
Dyfrakcja jest to zjawisko ugięcia się fali zauważalne, gdy przechodzi ona przez szczelinę o rozmiarach porównywalnych z długością fali.
Siatka dyfrakcyjna to układ szczelin wzajemnie równoległych i leżących w stałej odległości.
W siatkach dyfrakcyjnych szerokość szczelin jest rzędu długości fali świetlnej, więc natężenie prążków interferencyjnych jest prawie stałe.
Maksima interferencyjne (obszary wzmocnienia fali) występują w punktach ekranu, dla których różnica dróg jest wielokrotnością długości fali.
![]()
więc ![]()
Natomiast szerokość kątową maksimum głównego opisuje wzór: ![]()
gdzie ![]()
oznacza kąt występowania maksimum rzędu mSiatka dyfrakcyjna ma zdolność rozdzielczą ![]()
gdzie jest średnią długości fali dwóch linii widmowych ledwie rozróżnialnych, a jest różnicą długości fal między nimi.
Kryterium Rayleigh'a głosi, że dwa maksima są ledwie rozróżnialne, gdy ich odległość kątowa jest taka, że maksimum jednej linii przypada na minimum drugiej. Jeśli zastosujemy to kryterium, to możemy pokazać, że: R = N m, gdzie:
R--zdolność rozdzielcza, N--całkowita liczba nacięć, m--rząd obserwowanego widma.
W celu znalezienia stałej siatki dyfrakcyjnej d (czyli odległości między środkami dwóch sąsiednich szczelin) skorzystamy z równania ![]()
gdzie:
m - rząd widma, - długość fali, - kąt pod jakim obserwowane jest max. widma.W doświadczeniu użyjemy światła sodowego o długości fali ![]()
nm.
Kąt ![]()
wyrazimy natomiast przez różnicę położenia maksimum głównego ![]()
i położenia prążka ![]()
: ![]()
. Stąd: ![]()
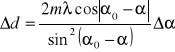
Pomiary
Położenie prążka zerowego: α0 z lewej =0026' i α0 z prawej 181020'
Δα = 0001'
Siatka B
Rząd |
Położenie |
kąt α |
sin α |
Stała siatki |
I z lewej |
190 |
180 34' |
0,3147 |
1873,53034 |
II z lewej |
400 21' |
390 55' |
0,6368 |
925,87939 |
I z prawej |
1640 30' |
160 09' |
0,2907 |
2028,20777 |
II z prawej |
1470 |
340 02' |
0,5621 |
1048,92367 |
Wynik |
1469,13529 |
|||
Wartość odchylenia standardowego przy pomocy błędu przeciętnego średniej arytmetycznej = współczynnik Fischera który wynosi dla 6 pomiarów 1,3 |
0,0281233 |
|||
Siatka C
Rząd |
Położenie |
kąt α |
sin α |
Stała siatki |
I z lewej |
150 10' |
140 44' |
0,2494 |
2364,07377 |
II z lewej |
10 50' |
10 24' |
0,0216 |
27296,296 |
I z prawej |
1670 45' |
130 75' |
0,2377 |
2480,43752 |
II z prawej |
1600 10' |
21010' |
0,36 |
1637,77677 |
Wynik |
844,646345 |
|||
Wartość odchylenia standardowego przy pomocy błędu przeciętnego średniej arytmetycznej = współczynnik Fischera który wynosi dla 6 pomiarów 1,3 |
8,28665 |
|||
Siatka D
Rząd |
Położenie |
kąt α |
sin α |
Stała siatki |
I z lewej |
10 20' |
00 54' |
0,0094 |
62723,4042 |
II z lewej |
80 10' |
7024' |
0,1295 |
4552,89575 |
III z lewej |
150 |
140 34' |
0,2477 |
2380,39874 |
I z prawej |
1670 30' |
130 50' |
0,2335 |
2525,05353 |
II z prawej |
1600 10' |
210 10' |
0,36 |
1637,7777 |
Wynik |
14963,888 |
|||
Wartość odchylenia standardowego przy pomocy błędu przeciętnego średniej arytmetycznej = współczynnik Fischera który wynosi dla 6 pomiarów 1,2 |
1,49996 |
|||
B=1,47 *10-6 ± 0037[um]
C=8,44*10-6 ± 0,82[um]
D=14,76*10-6 ±1,44[um]
Wyszukiwarka
Podobne podstrony:
Lab fiz 101, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
Lab fiz 104, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
Lab fiz 206, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
Lab fiz 303, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
302, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z 1 pracow
204pl, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z 1 prac
teoria do 109, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria
Ćw109mmm, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z 1 p
Tabelka 303, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
305przyklad, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
lab 1, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza
302-03, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, Laborki, laborki fiza, Fizyka
206e, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, Laborki, laborki fiza, Fizyka -
104, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, Laborki, laborki fiza, Fizyka -
104e, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, Laborki, laborki fiza, Fizyka -
100, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, Laborki, laborki fiza, Fizyka -
więcej podobnych podstron